2020-2021学年九年级数学北师大版5.1投影同步练习(Word版 有答案)
文档属性
| 名称 | 2020-2021学年九年级数学北师大版5.1投影同步练习(Word版 有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 206.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 22:45:31 | ||
图片预览

文档简介
第一节
投影
一、选择题
1、下列哪种光线形成的投影不是中心投影(
)
A.探照灯
B.太阳
C.手电筒
D.路灯
2、下列各种现象属于中心投影现象的是(
)
A.上午人走在路上的影子
B.晚上人走在路灯下的影子
C.中午用来乘凉的树影
D.早上升旗时地面上旗杆的影子
3、下图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),依图可判断形成该影子的光线为(
)
A.太阳光
B.灯光
C.太阳光或灯光
D.该影子实际上不可能存在
4、小刚走路时发现自己的影子越走越长,这是因为(
)
A.从路灯下走开,离路灯越来越远
B.走到路灯下,离路灯越来越近
C.路灯的灯光越来越暗
D.路灯的灯光越来越亮
5、下列四幅图中,可以表示两棵树在同一时刻阳光下的影子的是(
)
6、从日出到正午,校园里的旗杆的影长变化规律是(
)
A.逐渐变长
B.逐渐变短
C.先变长后变短
D.先变短后变长
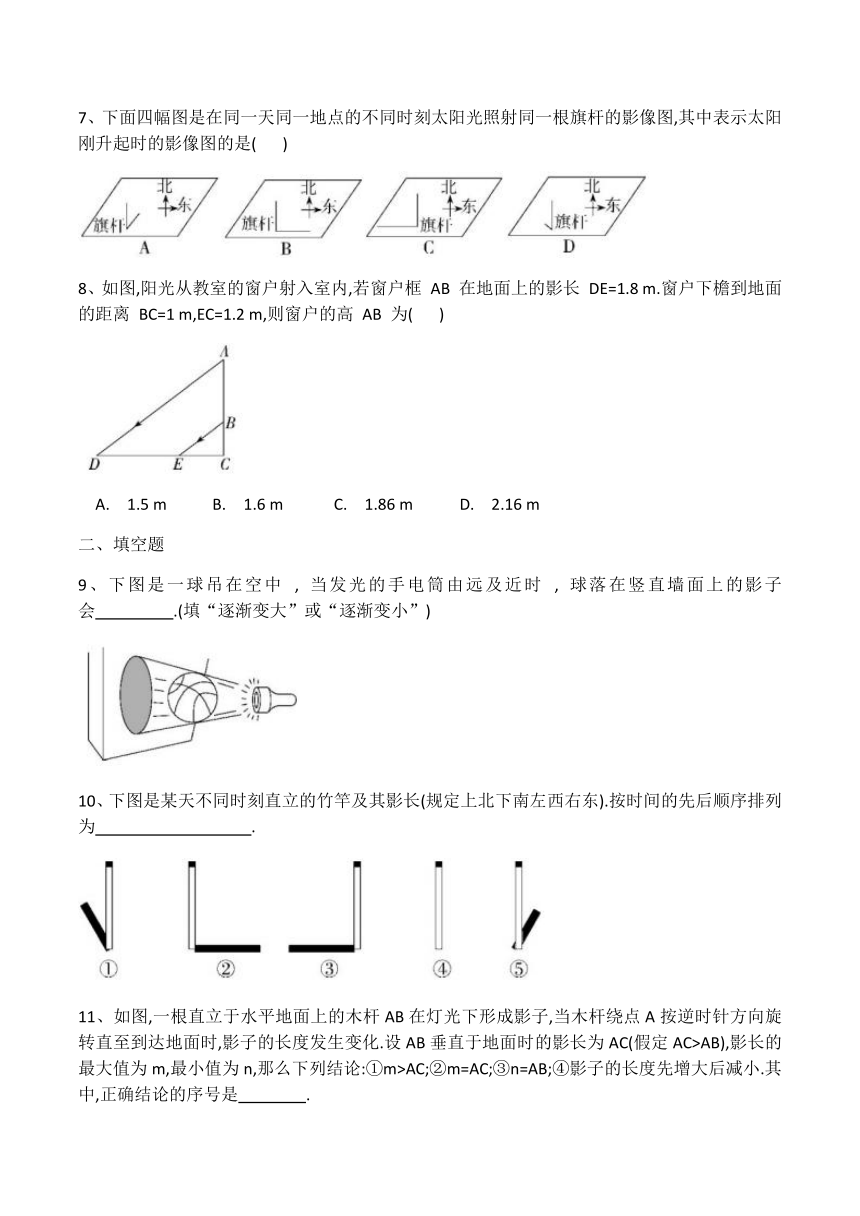
7、下面四幅图是在同一天同一地点的不同时刻太阳光照射同一根旗杆的影像图,其中表示太阳刚升起时的影像图的是(
)
8、如图,阳光从教室的窗户射入室内,若窗户框
AB
在地面上的影长
DE=1.8
m.窗户下檐到地面的距离
BC=1
m,EC=1.2
m,则窗户的高
AB
为(
)
A.
1.5
m
B.
1.6
m
C.
1.86
m
D.
2.16
m
二、填空题
9、下图是一球吊在空中
,
当发光的手电筒由远及近时
,
球落在竖直墙面上的影子会
.(填“逐渐变大”或“逐渐变小”)
10、下图是某天不同时刻直立的竹竿及其影长(规定上北下南左西右东).按时间的先后顺序排列为
.
11、如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕点A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC(假定AC>AB),影长的最大值为m,最小值为n,那么下列结论:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.其中,正确结论的序号是 ????.
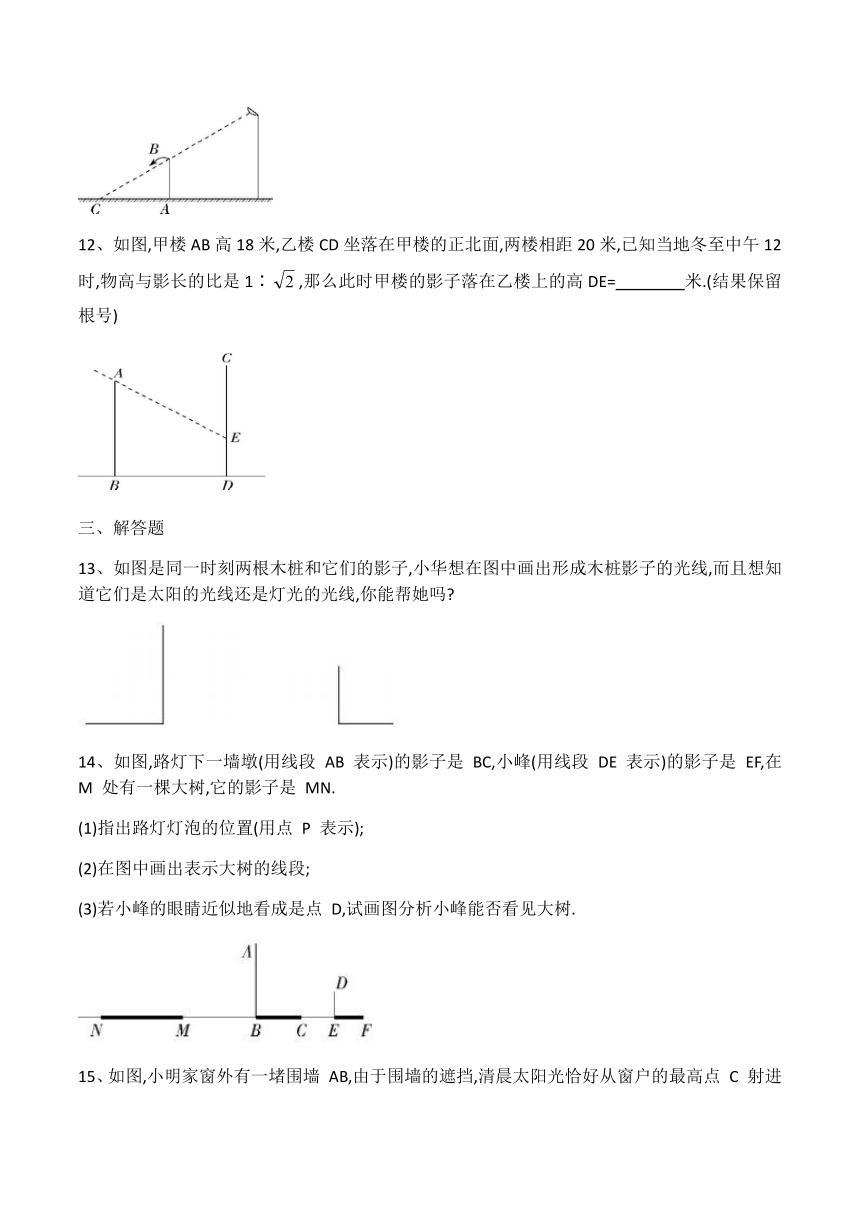
12、如图,甲楼AB高18米,乙楼CD坐落在甲楼的正北面,两楼相距20米,已知当地冬至中午12时,物高与影长的比是1∶,那么此时甲楼的影子落在乙楼上的高DE= ????米.(结果保留根号)
三、解答题
13、如图是同一时刻两根木桩和它们的影子,小华想在图中画出形成木桩影子的光线,而且想知道它们是太阳的光线还是灯光的光线,你能帮她吗?
14、如图,路灯下一墙墩(用线段
AB
表示)的影子是
BC,小峰(用线段
DE
表示)的影子是
EF,在
M
处有一棵大树,它的影子是
MN.
(1)指出路灯灯泡的位置(用点
P
表示);
(2)在图中画出表示大树的线段;
(3)若小峰的眼睛近似地看成是点
D,试画图分析小峰能否看见大树.
15、如图,小明家窗外有一堵围墙
AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点
C
射进房间的地板
F
处,中午太阳光恰好能从窗户的最低点
D
射进房间的地板
E
处,小明测得窗户距地面的高度
OD=0.8
m,窗高
CD=1.2
m,并测得
OE=0.8
m,OF=3
m,求围墙
AB
的高度.
16、如图,小明与同学合作利用太阳光线测量旗杆的高度,身高
1.6m
的小明落在地面上的影长BC
为
2.4
m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子
EG;
(2)若小明测得此刻旗杆落在地面上的影长
EG=16
m,请求出旗杆
DE
的高度.
17、下图是两棵树及其影子的情形.
(1)哪个图反映了阳光下的情形?哪个图反映了路灯下的情形?
(2)请画出图中表示小红影子的线段;
(3)阳光下小红的影长为
1.2
m,一棵树的影长为
2.4
m,小红的身高为
1.6
m,求这棵树的高度.
18、如图所示,AB
和
DE
是直立在地面上的两根立柱,AB=5
m,某一时刻,AB
在阳光下的投影BC=4
m.
(1)请你在图中画出此时
DE
在阳光下的投影,并简述画图步骤;
(2)在测量
AB
的投影长时,同时测出
DE
在阳光下的投影长为
6
m,请你计算
DE
的长.
答案
1.B
2.B
3.B
4.A
5.A
6.B
7.C
8.A
9.
逐渐变大
10.
③①④⑤②
11.
①③④
12.
(18-10)
13.
如图,分别过木桩的顶端和它们影子的顶端作直线,会发现两直线交于一点,则可知形成木桩影子的光线为灯光的光线.
14.
如图所示.
(1)点
P
是路灯灯泡的位置.
(2)线段
MG
是大树.
(3)MG
处于观测点
D
的盲区,所以小峰看不见大树.
15.
∵DO⊥BF,∴∠DOE=90°,
∵OD=0.8
m,OE=0.8
m,∴∠DEB=45°,
∵AB⊥BF,∴∠BAE=45°,∴AB=BE.
设
AB=EB=x
m,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,∴△ABF∽△COF,
∴=,即=,解得
x=4.4,
经检验,x=4.4
是原方程的解,且符合题意.故围墙
AB
的高度是
4.4
m.
16.
(1)如图所示,EG
即为所求.
(2)∵DG∥AC,∴∠ACB=∠DGE,
又∠ABC=∠DEG=90°,∴△ABC∽△DEG,
∴=,即=,∴DE=m,
∴旗杆
DE
的高度为m.
17.
(1)如图所示.图甲反映了阳光下的情形,图乙反映了路灯下的情形.
(2)图甲中
AB
是表示小红影子的线段,图乙中
CD
是表示小红影子的线段.
(3)设这棵树的高度为x
m,∵阳光下小红的影长为1.2
m,树的影长为
2.4
m,小红的身高为1.6
m,
∴=,解得
x=3.2.
经检验,x=3.2是原方程的解,且符合题意.答:这棵树的高度为
3.2
m.
18.
(1)如图:
作法:连接
AC,过点
D
作
DF∥AC,交直线
BE
于
F,
则
EF
就是
DE
在阳光下的投影.
(2)同一时刻,不同物体在阳光下的物高与影长成比例,∴=
.
∵AB=5
m,BC=4
m,EF=6
m,∴=,∴DE=7.5
m.
投影
一、选择题
1、下列哪种光线形成的投影不是中心投影(
)
A.探照灯
B.太阳
C.手电筒
D.路灯
2、下列各种现象属于中心投影现象的是(
)
A.上午人走在路上的影子
B.晚上人走在路灯下的影子
C.中午用来乘凉的树影
D.早上升旗时地面上旗杆的影子
3、下图是某学校操场上单杠(图中实线部分)在地面上的影子(图中虚线部分),依图可判断形成该影子的光线为(
)
A.太阳光
B.灯光
C.太阳光或灯光
D.该影子实际上不可能存在
4、小刚走路时发现自己的影子越走越长,这是因为(
)
A.从路灯下走开,离路灯越来越远
B.走到路灯下,离路灯越来越近
C.路灯的灯光越来越暗
D.路灯的灯光越来越亮
5、下列四幅图中,可以表示两棵树在同一时刻阳光下的影子的是(
)
6、从日出到正午,校园里的旗杆的影长变化规律是(
)
A.逐渐变长
B.逐渐变短
C.先变长后变短
D.先变短后变长
7、下面四幅图是在同一天同一地点的不同时刻太阳光照射同一根旗杆的影像图,其中表示太阳刚升起时的影像图的是(
)
8、如图,阳光从教室的窗户射入室内,若窗户框
AB
在地面上的影长
DE=1.8
m.窗户下檐到地面的距离
BC=1
m,EC=1.2
m,则窗户的高
AB
为(
)
A.
1.5
m
B.
1.6
m
C.
1.86
m
D.
2.16
m
二、填空题
9、下图是一球吊在空中
,
当发光的手电筒由远及近时
,
球落在竖直墙面上的影子会
.(填“逐渐变大”或“逐渐变小”)
10、下图是某天不同时刻直立的竹竿及其影长(规定上北下南左西右东).按时间的先后顺序排列为
.
11、如图,一根直立于水平地面上的木杆AB在灯光下形成影子,当木杆绕点A按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB垂直于地面时的影长为AC(假定AC>AB),影长的最大值为m,最小值为n,那么下列结论:①m>AC;②m=AC;③n=AB;④影子的长度先增大后减小.其中,正确结论的序号是 ????.
12、如图,甲楼AB高18米,乙楼CD坐落在甲楼的正北面,两楼相距20米,已知当地冬至中午12时,物高与影长的比是1∶,那么此时甲楼的影子落在乙楼上的高DE= ????米.(结果保留根号)
三、解答题
13、如图是同一时刻两根木桩和它们的影子,小华想在图中画出形成木桩影子的光线,而且想知道它们是太阳的光线还是灯光的光线,你能帮她吗?
14、如图,路灯下一墙墩(用线段
AB
表示)的影子是
BC,小峰(用线段
DE
表示)的影子是
EF,在
M
处有一棵大树,它的影子是
MN.
(1)指出路灯灯泡的位置(用点
P
表示);
(2)在图中画出表示大树的线段;
(3)若小峰的眼睛近似地看成是点
D,试画图分析小峰能否看见大树.
15、如图,小明家窗外有一堵围墙
AB,由于围墙的遮挡,清晨太阳光恰好从窗户的最高点
C
射进房间的地板
F
处,中午太阳光恰好能从窗户的最低点
D
射进房间的地板
E
处,小明测得窗户距地面的高度
OD=0.8
m,窗高
CD=1.2
m,并测得
OE=0.8
m,OF=3
m,求围墙
AB
的高度.
16、如图,小明与同学合作利用太阳光线测量旗杆的高度,身高
1.6m
的小明落在地面上的影长BC
为
2.4
m.
(1)请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子
EG;
(2)若小明测得此刻旗杆落在地面上的影长
EG=16
m,请求出旗杆
DE
的高度.
17、下图是两棵树及其影子的情形.
(1)哪个图反映了阳光下的情形?哪个图反映了路灯下的情形?
(2)请画出图中表示小红影子的线段;
(3)阳光下小红的影长为
1.2
m,一棵树的影长为
2.4
m,小红的身高为
1.6
m,求这棵树的高度.
18、如图所示,AB
和
DE
是直立在地面上的两根立柱,AB=5
m,某一时刻,AB
在阳光下的投影BC=4
m.
(1)请你在图中画出此时
DE
在阳光下的投影,并简述画图步骤;
(2)在测量
AB
的投影长时,同时测出
DE
在阳光下的投影长为
6
m,请你计算
DE
的长.
答案
1.B
2.B
3.B
4.A
5.A
6.B
7.C
8.A
9.
逐渐变大
10.
③①④⑤②
11.
①③④
12.
(18-10)
13.
如图,分别过木桩的顶端和它们影子的顶端作直线,会发现两直线交于一点,则可知形成木桩影子的光线为灯光的光线.
14.
如图所示.
(1)点
P
是路灯灯泡的位置.
(2)线段
MG
是大树.
(3)MG
处于观测点
D
的盲区,所以小峰看不见大树.
15.
∵DO⊥BF,∴∠DOE=90°,
∵OD=0.8
m,OE=0.8
m,∴∠DEB=45°,
∵AB⊥BF,∴∠BAE=45°,∴AB=BE.
设
AB=EB=x
m,
∵AB⊥BF,CO⊥BF,
∴AB∥CO,∴△ABF∽△COF,
∴=,即=,解得
x=4.4,
经检验,x=4.4
是原方程的解,且符合题意.故围墙
AB
的高度是
4.4
m.
16.
(1)如图所示,EG
即为所求.
(2)∵DG∥AC,∴∠ACB=∠DGE,
又∠ABC=∠DEG=90°,∴△ABC∽△DEG,
∴=,即=,∴DE=m,
∴旗杆
DE
的高度为m.
17.
(1)如图所示.图甲反映了阳光下的情形,图乙反映了路灯下的情形.
(2)图甲中
AB
是表示小红影子的线段,图乙中
CD
是表示小红影子的线段.
(3)设这棵树的高度为x
m,∵阳光下小红的影长为1.2
m,树的影长为
2.4
m,小红的身高为1.6
m,
∴=,解得
x=3.2.
经检验,x=3.2是原方程的解,且符合题意.答:这棵树的高度为
3.2
m.
18.
(1)如图:
作法:连接
AC,过点
D
作
DF∥AC,交直线
BE
于
F,
则
EF
就是
DE
在阳光下的投影.
(2)同一时刻,不同物体在阳光下的物高与影长成比例,∴=
.
∵AB=5
m,BC=4
m,EF=6
m,∴=,∴DE=7.5
m.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
