人教版数学八年级上册13.3.2 等边三角形 同步练习(Word版 附答案)
文档属性
| 名称 | 人教版数学八年级上册13.3.2 等边三角形 同步练习(Word版 附答案) | 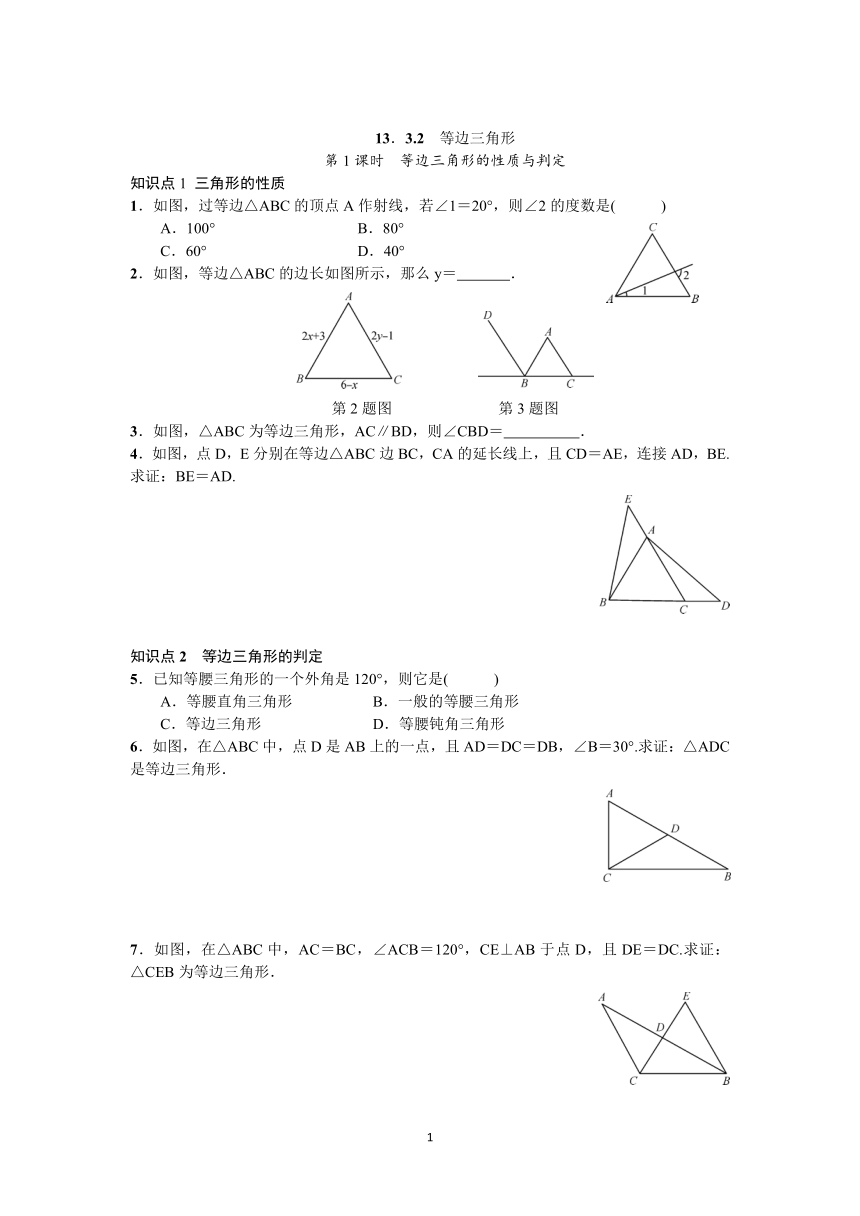 | |
| 格式 | docx | ||
| 文件大小 | 120.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-05 22:48:45 | ||
图片预览



文档简介
13.3.2 等边三角形
第1课时 等边三角形的性质与判定
知识点1 三角形的性质
1.如图,过等边△ABC的顶点A作射线,若∠1=20°,则∠2的度数是( )
419227060960A.100° B.80°
C.60° D.40°
2.如图,等边△ABC的边长如图所示,那么y= .
第2题图 第3题图
3.如图,△ABC为等边三角形,AC∥BD,则∠CBD= .
4.如图,点D,E分别在等边△ABC边BC,CA的延长线上,且CD=AE,连接AD,BE.求证:BE=AD.
知识点2 等边三角形的判定
5.已知等腰三角形的一个外角是120°,则它是( )
A.等腰直角三角形 B.一般的等腰三角形
C.等边三角形 D.等腰钝角三角形
6.如图,在△ABC中,点D是AB上的一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
7.如图,在△ABC中,AC=BC,∠ACB=120°,CE⊥AB于点D,且DE=DC.求证:△CEB为等边三角形.
8.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
第8题图 第9题图
9.如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )
A.60° B.55° C.45° D.不能确定
10.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆OA=OB=18 cm,若衣架收拢时,∠AOB=60°,如图2,则此时A,B两点之间的距离是 cm.
11.如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形ODC,连接AC和BD,相交于点E,连接BC.求∠AEB的大小.
12.如图,已知△ABC是边长为6 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC匀速运动,其中点P运动的速度是1 cm/s,点Q运动的速度是2 cm/s,当点Q到达点C时,P,Q两点都停止运动.设运动时间为t s,当t=2时,判断△BPQ的形状,并说明理由.
13.如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD,DE,EC三者有什么关系?写出你的判断过程.
第2课时 含30°角的直角三角形的性质
知识点 含30°角的直角三角形的性质
1.在△ABC中,∠A∶∠B∶∠C=1∶2∶3,最小边BC=4 cm,则最长边AB的长是( )
A.5 cm B.6 cm C. cm D.8 cm
2.如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD等于( )
A.3 B.4 C.5 D.6
第2题图 第3题图
3.如图,△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8 cm,则BD= ,BE= .
4.等腰三角形顶角为30°,腰长是4 cm,则三角形的面积是 .
5.如图是某房屋顶框架的示意图,其中,AB=AC,AD⊥BC,∠BAC=120°,AD=3.5 m,求∠B,∠C,∠BAD的度数和AB的长度.
6.如图,在Rt△ABC中,∠A=30°,DE垂直平分AB,垂足为点E,交AC于点D,连接BD.若DE=2,则AC的长为( )
A.4 B.6 C.8 D.10
第6题图 第7题图
7.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN.若MN=2,则OM=( )
A.3 B.4 C.5 D.6
8.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,连接AE,BE=6 cm,则AC的长为 .
9.如图,在等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数;
(2)求证:M是BE的中点.
10.某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°.求:
(1)此时轮船与小岛P的距离BP是多少海里?
(2)小岛点P方圆3海里内有暗礁,如果轮船继续向东航行,请问轮船有没有触礁的危险?请说明理由.
参考答案:
13.3.2 等边三角形
第1课时 等边三角形的性质与判定
1.B
2.3.
3.120°.
4.证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°.
∴∠BAE=∠ACD=120°.
在△BAE和△ACD中,
∴△BAE≌△ACD(SAS).
∴BE=AD.
5.C
6.证明:∵DC=DB,
∴∠B=∠DCB=30°.
∴∠ADC=∠DCB+∠B=60°.
又∵AD=DC,
∴△ADC是等边三角形.
7.∴BC=BE.
∵AC=BC,∠ACB=120°,CE⊥AB,
∴∠ECB=60°.
又∵BC=BE,
∴△CEB为等边三角形.
8.A
9.A
10.18.
11.解:∵△DOC和△ABO都是等边三角形,且点O是线段AD的中点,
∴OD=DC=OC=OB=OA,∠ADC=∠DAB=60°.
在△DBA和△ACD中,
∴△DBA≌△ACD(SAS).∴∠BDA=∠CAD.
∵OD=OB,
∴∠ODB=∠OBD.
又∵∠BDA+∠OBD=∠BOA=60°,
∴∠BDA=30°.
∴∠CAD=30°.
∵∠AEB=∠BDA+∠CAD,
∴∠AEB=60°.
12.解:△BPQ是等边三角形.理由:
当t=2时,
AP=2×1=2(cm),
BQ=2×2=4(cm).
∴BP=AB-AP=6-2=4(cm).
∴BQ=BP.
又∵△ABC是等边三角形,
∴∠B=60°.
∴△BPQ是等边三角形.
13.解:(1)△ODE是等边三角形.
理由:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵OD∥AB,OE∥AC.
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°.
∴△ODE是等边三角形.
(2)BD=DE=EC.
理由:∵OB平分∠ABC,且∠ABC=60°,
∴∠ABO=∠OBD=30°.
∵OD∥AB,
∴∠BOD=∠ABO=30°.
∴∠DBO=∠DOB.
∴DB=DO.
同理:EC=EO.
∵△ODE是等边三角形,
∴DE=OD=OE.
∴BD=DE=EC.
第2课时 含30°角的直角三角形的性质
1.D
2.A
3.2__cm.
4.4__cm2.
5.解:∵AB=AC,∴∠B=∠C=×(180°-120°)=30°.
∵AD⊥BC,
∴∠ADB=90°,∠BAD=∠BAC=60°.
又∵∠B=30°,
∴AB=2AD=7 m.
6.B
7.C
8.3__cm.
9.
解:(1)∵△ABC是等边三角形,
∴∠ACB=∠ABC=60°.
又∵CE=CD,∴∠E=∠CDE.
又∵∠ACB=∠E+∠CDE,
∴∠E=∠ACB=30°.
(2)证明:连接BD,
∵等边△ABC中,D是AC的中点,
∴∠DBC=∠ABC=×60°=30°.
由(1)知∠E=30°,
∴∠DBC=∠E=30°,∴DB=DE.
又∵DM⊥BC,
∴M是BE的中点.
10.
解:(1)过点P作PD⊥AB于点D.
∵∠PBD=90°-60°=30°,∠PAB=90°-75°=15°,
∴∠APB=30°-15°=15°.
∴∠PAB=∠APB.∴BP=AB=7海里.
(2)∵∠PBD=30°,∠PDB=90°,
∴PD=PB=3.5海里.
∵3.5>3,
∴该轮船继续向东航行,没有触礁的危险.
第1课时 等边三角形的性质与判定
知识点1 三角形的性质
1.如图,过等边△ABC的顶点A作射线,若∠1=20°,则∠2的度数是( )
419227060960A.100° B.80°
C.60° D.40°
2.如图,等边△ABC的边长如图所示,那么y= .
第2题图 第3题图
3.如图,△ABC为等边三角形,AC∥BD,则∠CBD= .
4.如图,点D,E分别在等边△ABC边BC,CA的延长线上,且CD=AE,连接AD,BE.求证:BE=AD.
知识点2 等边三角形的判定
5.已知等腰三角形的一个外角是120°,则它是( )
A.等腰直角三角形 B.一般的等腰三角形
C.等边三角形 D.等腰钝角三角形
6.如图,在△ABC中,点D是AB上的一点,且AD=DC=DB,∠B=30°.求证:△ADC是等边三角形.
7.如图,在△ABC中,AC=BC,∠ACB=120°,CE⊥AB于点D,且DE=DC.求证:△CEB为等边三角形.
8.如图,等边三角形ABC中,AD⊥BC,垂足为D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )
A.15° B.30° C.45° D.60°
第8题图 第9题图
9.如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )
A.60° B.55° C.45° D.不能确定
10.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆OA=OB=18 cm,若衣架收拢时,∠AOB=60°,如图2,则此时A,B两点之间的距离是 cm.
11.如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形ODC,连接AC和BD,相交于点E,连接BC.求∠AEB的大小.
12.如图,已知△ABC是边长为6 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC匀速运动,其中点P运动的速度是1 cm/s,点Q运动的速度是2 cm/s,当点Q到达点C时,P,Q两点都停止运动.设运动时间为t s,当t=2时,判断△BPQ的形状,并说明理由.
13.如图,在等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
(1)试判定△ODE的形状,并说明你的理由;
(2)线段BD,DE,EC三者有什么关系?写出你的判断过程.
第2课时 含30°角的直角三角形的性质
知识点 含30°角的直角三角形的性质
1.在△ABC中,∠A∶∠B∶∠C=1∶2∶3,最小边BC=4 cm,则最长边AB的长是( )
A.5 cm B.6 cm C. cm D.8 cm
2.如图,在△ABC中,∠C=90°,∠ABC=60°,BD平分∠ABC,若AD=6,则CD等于( )
A.3 B.4 C.5 D.6
第2题图 第3题图
3.如图,△ABC是等边三角形,AD⊥BC,DE⊥AB,若AB=8 cm,则BD= ,BE= .
4.等腰三角形顶角为30°,腰长是4 cm,则三角形的面积是 .
5.如图是某房屋顶框架的示意图,其中,AB=AC,AD⊥BC,∠BAC=120°,AD=3.5 m,求∠B,∠C,∠BAD的度数和AB的长度.
6.如图,在Rt△ABC中,∠A=30°,DE垂直平分AB,垂足为点E,交AC于点D,连接BD.若DE=2,则AC的长为( )
A.4 B.6 C.8 D.10
第6题图 第7题图
7.如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN.若MN=2,则OM=( )
A.3 B.4 C.5 D.6
8.如图,在△ABC中,∠ACB=90°,∠B=15°,DE垂直平分AB,交BC于点E,连接AE,BE=6 cm,则AC的长为 .
9.如图,在等边△ABC中,D是AC的中点,E是BC延长线上的一点,且CE=CD,DM⊥BC,垂足为M.
(1)求∠E的度数;
(2)求证:M是BE的中点.
10.某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°.求:
(1)此时轮船与小岛P的距离BP是多少海里?
(2)小岛点P方圆3海里内有暗礁,如果轮船继续向东航行,请问轮船有没有触礁的危险?请说明理由.
参考答案:
13.3.2 等边三角形
第1课时 等边三角形的性质与判定
1.B
2.3.
3.120°.
4.证明:∵△ABC是等边三角形,
∴AB=AC,∠BAC=∠ACB=60°.
∴∠BAE=∠ACD=120°.
在△BAE和△ACD中,
∴△BAE≌△ACD(SAS).
∴BE=AD.
5.C
6.证明:∵DC=DB,
∴∠B=∠DCB=30°.
∴∠ADC=∠DCB+∠B=60°.
又∵AD=DC,
∴△ADC是等边三角形.
7.∴BC=BE.
∵AC=BC,∠ACB=120°,CE⊥AB,
∴∠ECB=60°.
又∵BC=BE,
∴△CEB为等边三角形.
8.A
9.A
10.18.
11.解:∵△DOC和△ABO都是等边三角形,且点O是线段AD的中点,
∴OD=DC=OC=OB=OA,∠ADC=∠DAB=60°.
在△DBA和△ACD中,
∴△DBA≌△ACD(SAS).∴∠BDA=∠CAD.
∵OD=OB,
∴∠ODB=∠OBD.
又∵∠BDA+∠OBD=∠BOA=60°,
∴∠BDA=30°.
∴∠CAD=30°.
∵∠AEB=∠BDA+∠CAD,
∴∠AEB=60°.
12.解:△BPQ是等边三角形.理由:
当t=2时,
AP=2×1=2(cm),
BQ=2×2=4(cm).
∴BP=AB-AP=6-2=4(cm).
∴BQ=BP.
又∵△ABC是等边三角形,
∴∠B=60°.
∴△BPQ是等边三角形.
13.解:(1)△ODE是等边三角形.
理由:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵OD∥AB,OE∥AC.
∴∠ODE=∠ABC=60°,∠OED=∠ACB=60°.
∴△ODE是等边三角形.
(2)BD=DE=EC.
理由:∵OB平分∠ABC,且∠ABC=60°,
∴∠ABO=∠OBD=30°.
∵OD∥AB,
∴∠BOD=∠ABO=30°.
∴∠DBO=∠DOB.
∴DB=DO.
同理:EC=EO.
∵△ODE是等边三角形,
∴DE=OD=OE.
∴BD=DE=EC.
第2课时 含30°角的直角三角形的性质
1.D
2.A
3.2__cm.
4.4__cm2.
5.解:∵AB=AC,∴∠B=∠C=×(180°-120°)=30°.
∵AD⊥BC,
∴∠ADB=90°,∠BAD=∠BAC=60°.
又∵∠B=30°,
∴AB=2AD=7 m.
6.B
7.C
8.3__cm.
9.
解:(1)∵△ABC是等边三角形,
∴∠ACB=∠ABC=60°.
又∵CE=CD,∴∠E=∠CDE.
又∵∠ACB=∠E+∠CDE,
∴∠E=∠ACB=30°.
(2)证明:连接BD,
∵等边△ABC中,D是AC的中点,
∴∠DBC=∠ABC=×60°=30°.
由(1)知∠E=30°,
∴∠DBC=∠E=30°,∴DB=DE.
又∵DM⊥BC,
∴M是BE的中点.
10.
解:(1)过点P作PD⊥AB于点D.
∵∠PBD=90°-60°=30°,∠PAB=90°-75°=15°,
∴∠APB=30°-15°=15°.
∴∠PAB=∠APB.∴BP=AB=7海里.
(2)∵∠PBD=30°,∠PDB=90°,
∴PD=PB=3.5海里.
∵3.5>3,
∴该轮船继续向东航行,没有触礁的危险.
