湘教版八年级数学上册第2章三角形单元综合试卷(word版含答案)
文档属性
| 名称 | 湘教版八年级数学上册第2章三角形单元综合试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 08:39:02 | ||
图片预览

文档简介
第2章
三角形
一、选择题(共10小题;共50分)
1.
如图,在
中,,,
是
上一点.将
沿
折叠,使
点落在
边上的
处,则
等于?(
)
A.
B.
C.
D.
2.
如图所示,,,,则
,此时运用的判定定理是
A.
B.
C.
D.
3.
如图,已知
,求作一点
,使
到
的两边的距离相等,且
.下列
确定
点的方法正确的是?(
)
A.
为
、
两角平分线的交点
B.
为
的角平分线与
的垂直平分线的交点
C.
为
、
两边上的高的交点
D.
为
、
两边的垂直平分线的交点
4.
下列语句不是命题的有?(
)①两点之间,线段最短;
②不许大声讲话;
③连接
,
两点;
④鸟是动物;
⑤不相交的两条直线叫做平行线;
⑥无论
为怎样的自然数,式子
的值都是质数吗?
A.
个
B.
个
C.
个
D.
个
5.
如果一个三角形的两边长分别为
和
,则第三边长可能是?(
)
A.
B.
C.
D.
6.
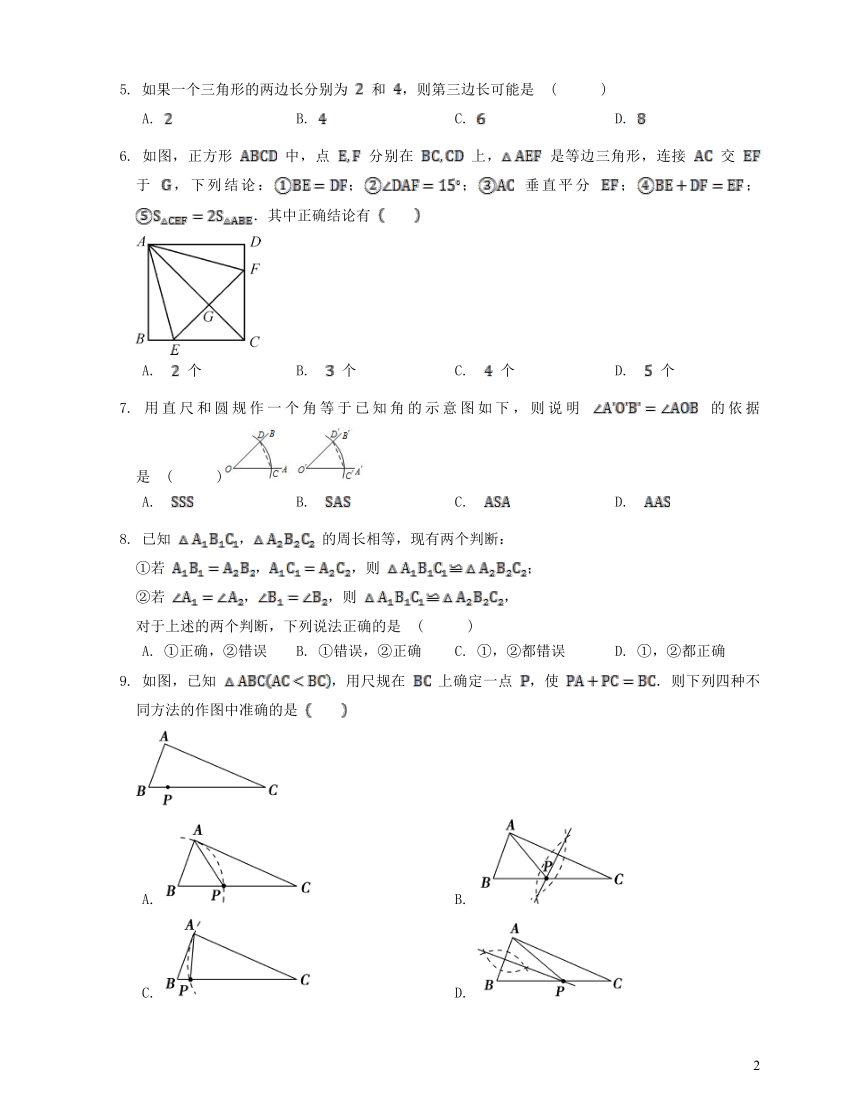
如图,正方形
中,点
分别在
上,
是等边三角形,连接
交
于
,下列结论:;;
垂直平分
;;.其中正确结论有
A.
个
B.
个
C.
个
D.
个
7.
用直尺和圆规作一个角等于已知角的示意图如下,则说明
的依据是?(
)
A.
B.
C.
D.
8.
已知
,
的周长相等,现有两个判断:
①若
,,则
;
②若
,,则
,
对于上述的两个判断,下列说法正确的是?(
)
A.
①正确,②错误
B.
①错误,②正确
C.
①,②都错误
D.
①,②都正确
9.
如图,已知
,用尺规在
上确定一点
,使
.则下列四种不同方法的作图中准确的是
A.
B.
C.
D.
10.
在建筑工地我们常可看见如图1所示,用木条
固定矩形门框
的情形.这种做法根据?(
).
A.
两点之间线段最短
B.
两点确定一条直线
C.
三角形的稳定性
D.
矩形的四个角都是直角
二、填空题(共10小题;共50分)
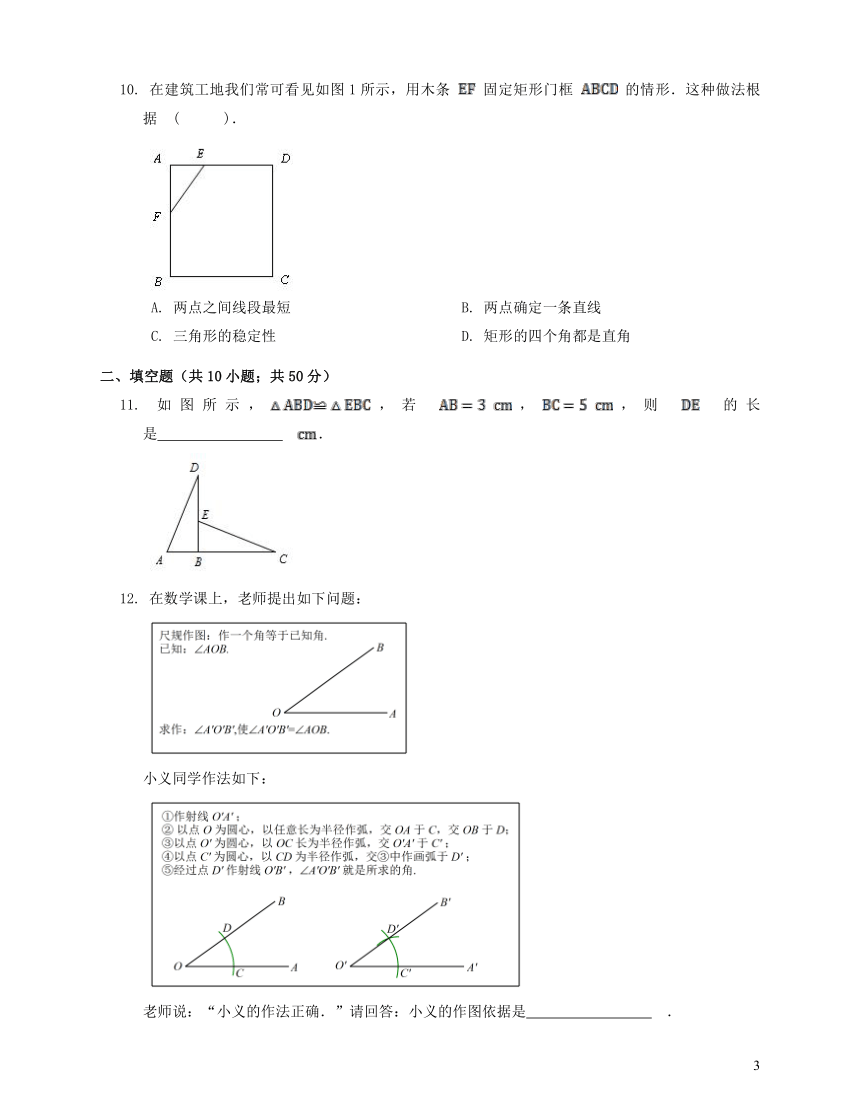
11.
如图所示,,若
,,则
的长是
?
.
12.
在数学课上,老师提出如下问题:
小义同学作法如下:
老师说:“小义的作法正确.”请回答:小义的作图依据是
?
.
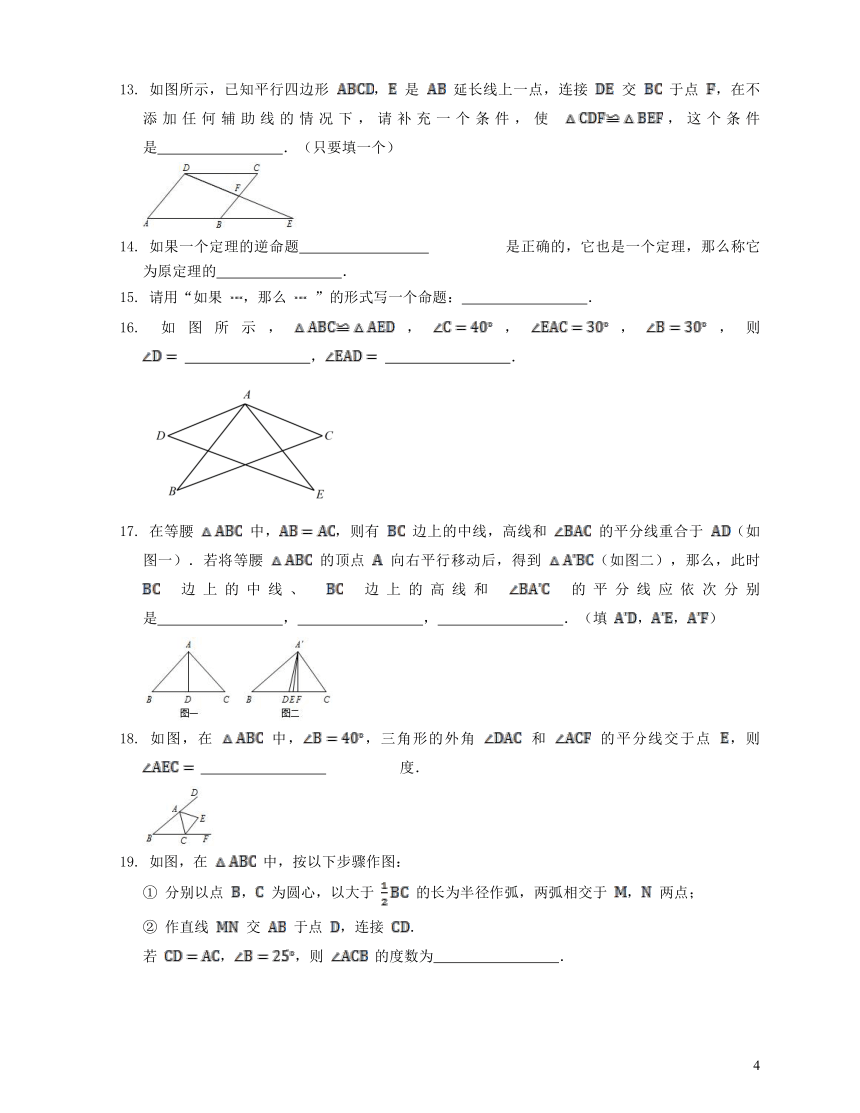
13.
如图所示,已知平行四边形
,
是
延长线上一点,连接
交
于点
,在不添加任何辅助线的情况下,请补充一个条件,使
,这个条件是
?.(只要填一个)
14.
如果一个定理的逆命题
?
是正确的,它也是一个定理,那么称它为原定理的
?.
15.
请用“如果
,那么
”的形式写一个命题:
?.
16.
如图所示,,,,,则
?,
?.
17.
在等腰
中,,则有
边上的中线,高线和
的平分线重合于
(如图一).若将等腰
的顶点
向右平行移动后,得到
(如图二),那么,此时
边上的中线、
边上的高线和
的平分线应依次分别是
?,
?,
?.(填
,,)
18.
如图,在
中,,三角形的外角
和
的平分线交于点
,则
?
度.
19.
如图,在
中,按以下步骤作图:
①
分别以点
,
为圆心,以大于
的长为半径作弧,两弧相交于
,
两点;
②
作直线
交
于点
,连接
.
若
,,则
的度数为
?.
20.
各边长度都是整数,最大边长为
的三角形共有
?
个.
三、解答题(共5小题;共65分)
21.
如图,,,,求证:.
22.
如图,在
中,.
(1)
用尺规在边
上求作一点
,使
(不写作法,保留作图痕迹);
(2)
连接
,当
为
?
度时,
平分
.
23.
已知:如图所示,点
、
分别在等边
的边
、
上,且
,
与
相交于点
.
(1)
求证:
(2)
求
的度数.
24.
如图,在
中,
是
上的高,
平分
,,.求
与
的度数.
25.
如图,在
中,,,,垂足分别为点
,,点
为
中点,
与
,
分别交于点
,,.
(1)
线段
与
相等吗,若相等给予证明,若不相等请说明理由;
(2)
求证:.
答案
第一部分
1.
D
2.
C
3.
B
4.
B
5.
B
6.
C
7.
A
8.
D
9.
D
10.
C
第二部分
11.
12.
三边分别相等的两个三角形全等;全等三角形对应角相等(写出其中一个即可)
13.
或
或
.
14.
经过证明;逆定理
15.
如果
,,那么
.
16.
;
17.
,,
18.
19.
20.
第三部分
21.
,
,
即
.
又
,,
.
.
22.
(1)
如图所示.
(2)
23.
(1)
是等边三角形
,
.
,
.
(2)
,
.
,
.
24.
,,
.
又
平分
,
.
又
,
.
.
25.
(1)
,,
,,,
,,
在
和
中,
,,,
,
(2)
连接CG.
为
的中点,,
垂直平分
,
,
,,
在
和
中,
,,,
,
.
在
中,
由勾股定理得
,
1
三角形
一、选择题(共10小题;共50分)
1.
如图,在
中,,,
是
上一点.将
沿
折叠,使
点落在
边上的
处,则
等于?(
)
A.
B.
C.
D.
2.
如图所示,,,,则
,此时运用的判定定理是
A.
B.
C.
D.
3.
如图,已知
,求作一点
,使
到
的两边的距离相等,且
.下列
确定
点的方法正确的是?(
)
A.
为
、
两角平分线的交点
B.
为
的角平分线与
的垂直平分线的交点
C.
为
、
两边上的高的交点
D.
为
、
两边的垂直平分线的交点
4.
下列语句不是命题的有?(
)①两点之间,线段最短;
②不许大声讲话;
③连接
,
两点;
④鸟是动物;
⑤不相交的两条直线叫做平行线;
⑥无论
为怎样的自然数,式子
的值都是质数吗?
A.
个
B.
个
C.
个
D.
个
5.
如果一个三角形的两边长分别为
和
,则第三边长可能是?(
)
A.
B.
C.
D.
6.
如图,正方形
中,点
分别在
上,
是等边三角形,连接
交
于
,下列结论:;;
垂直平分
;;.其中正确结论有
A.
个
B.
个
C.
个
D.
个
7.
用直尺和圆规作一个角等于已知角的示意图如下,则说明
的依据是?(
)
A.
B.
C.
D.
8.
已知
,
的周长相等,现有两个判断:
①若
,,则
;
②若
,,则
,
对于上述的两个判断,下列说法正确的是?(
)
A.
①正确,②错误
B.
①错误,②正确
C.
①,②都错误
D.
①,②都正确
9.
如图,已知
,用尺规在
上确定一点
,使
.则下列四种不同方法的作图中准确的是
A.
B.
C.
D.
10.
在建筑工地我们常可看见如图1所示,用木条
固定矩形门框
的情形.这种做法根据?(
).
A.
两点之间线段最短
B.
两点确定一条直线
C.
三角形的稳定性
D.
矩形的四个角都是直角
二、填空题(共10小题;共50分)
11.
如图所示,,若
,,则
的长是
?
.
12.
在数学课上,老师提出如下问题:
小义同学作法如下:
老师说:“小义的作法正确.”请回答:小义的作图依据是
?
.
13.
如图所示,已知平行四边形
,
是
延长线上一点,连接
交
于点
,在不添加任何辅助线的情况下,请补充一个条件,使
,这个条件是
?.(只要填一个)
14.
如果一个定理的逆命题
?
是正确的,它也是一个定理,那么称它为原定理的
?.
15.
请用“如果
,那么
”的形式写一个命题:
?.
16.
如图所示,,,,,则
?,
?.
17.
在等腰
中,,则有
边上的中线,高线和
的平分线重合于
(如图一).若将等腰
的顶点
向右平行移动后,得到
(如图二),那么,此时
边上的中线、
边上的高线和
的平分线应依次分别是
?,
?,
?.(填
,,)
18.
如图,在
中,,三角形的外角
和
的平分线交于点
,则
?
度.
19.
如图,在
中,按以下步骤作图:
①
分别以点
,
为圆心,以大于
的长为半径作弧,两弧相交于
,
两点;
②
作直线
交
于点
,连接
.
若
,,则
的度数为
?.
20.
各边长度都是整数,最大边长为
的三角形共有
?
个.
三、解答题(共5小题;共65分)
21.
如图,,,,求证:.
22.
如图,在
中,.
(1)
用尺规在边
上求作一点
,使
(不写作法,保留作图痕迹);
(2)
连接
,当
为
?
度时,
平分
.
23.
已知:如图所示,点
、
分别在等边
的边
、
上,且
,
与
相交于点
.
(1)
求证:
(2)
求
的度数.
24.
如图,在
中,
是
上的高,
平分
,,.求
与
的度数.
25.
如图,在
中,,,,垂足分别为点
,,点
为
中点,
与
,
分别交于点
,,.
(1)
线段
与
相等吗,若相等给予证明,若不相等请说明理由;
(2)
求证:.
答案
第一部分
1.
D
2.
C
3.
B
4.
B
5.
B
6.
C
7.
A
8.
D
9.
D
10.
C
第二部分
11.
12.
三边分别相等的两个三角形全等;全等三角形对应角相等(写出其中一个即可)
13.
或
或
.
14.
经过证明;逆定理
15.
如果
,,那么
.
16.
;
17.
,,
18.
19.
20.
第三部分
21.
,
,
即
.
又
,,
.
.
22.
(1)
如图所示.
(2)
23.
(1)
是等边三角形
,
.
,
.
(2)
,
.
,
.
24.
,,
.
又
平分
,
.
又
,
.
.
25.
(1)
,,
,,,
,,
在
和
中,
,,,
,
(2)
连接CG.
为
的中点,,
垂直平分
,
,
,,
在
和
中,
,,,
,
.
在
中,
由勾股定理得
,
1
同课章节目录
