第3课时 解决双直角三角形问题 课件(共18张)
文档属性
| 名称 | 第3课时 解决双直角三角形问题 课件(共18张) |  | |
| 格式 | zip | ||
| 文件大小 | 413.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 10:43:33 | ||
图片预览




文档简介
(共18张PPT)
第3课时
解决双直角三角形问题
23.2
解直角三角形及其应用
沪科版
九年级数学上册
教学课件
学习目标
【知识与技能】
比较熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
【过程与方法】
通过学习进一步掌握解直角三角形的方法.
【情感态度】
培养学生把实际问题转化为数学问题的能力.
【教学重点】
应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
【教学难点】
选用恰当的直角三角形,解题思路分析.
新课导入
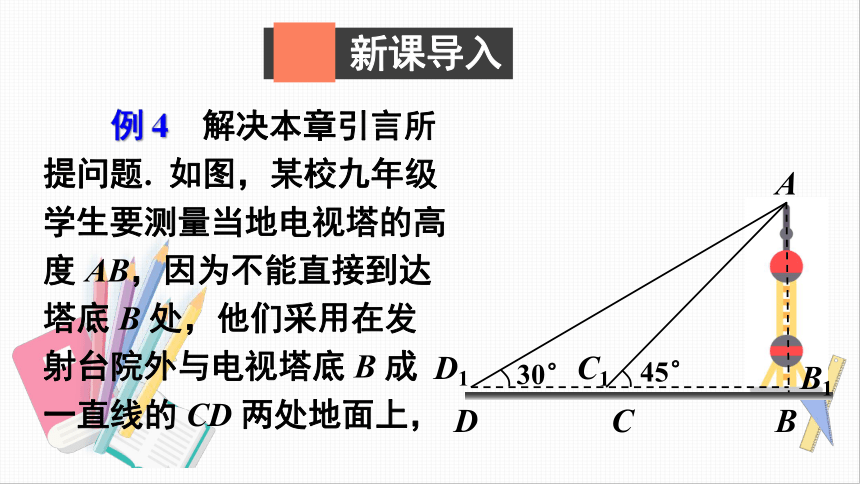
例
4
解决本章引言所提问题.
如图,某校九年级学生要测量当地电视塔的高度
AB,因为不能直接到达塔底
B
处,他们采用在发射台院外与电视塔底
B
成一直线的
CD
两处地面上,
A
B
B1
C
D
C1
D1
30°
45°
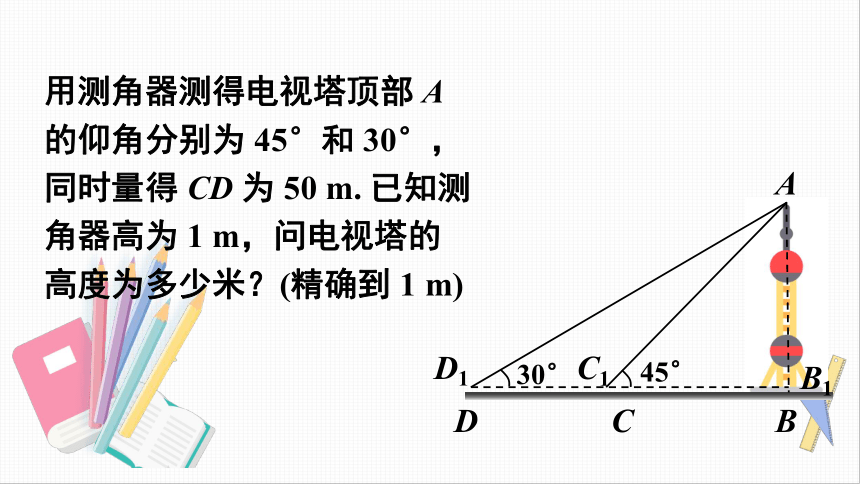
用测角器测得电视塔顶部
A
的仰角分别为
45°和
30°,同时量得
CD
为
50
m.
已知测角器高为
1
m,问电视塔的高度为多少米?(精确到
1
m)
A
B
B1
C
D
C1
D1
30°
45°
新课探究
A
B
B1
C
D
C1
D1
30°
45°
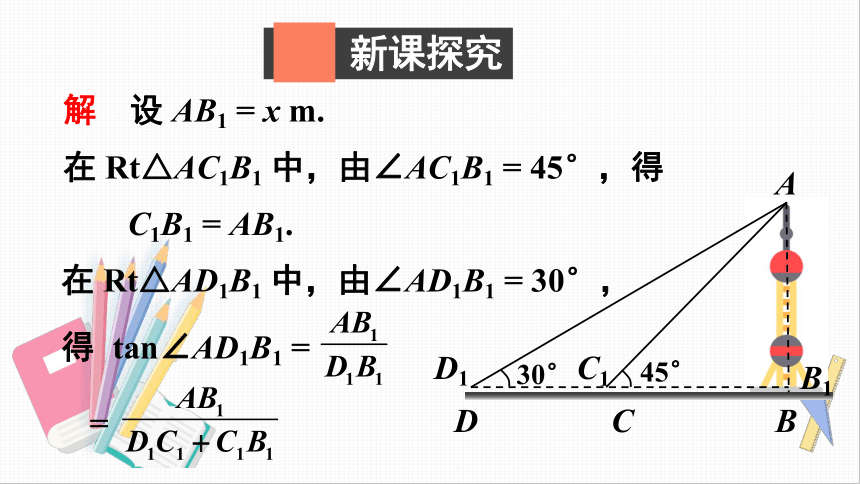
解
设
AB1
=
x
m.
在
Rt△AC1B1
中,由∠AC1B1
=
45°,得
C1B1
=
AB1.
在
Rt△AD1B1
中,由∠AD1B1
=
30°,
得
tan∠AD1B1
=
=
A
B
B1
C
D
C1
D1
30°
45°
即
解方程,得
x
=
25(
+
1)≈
68.
∴
AB
=
AB1
+
BB1
≈
68
+
1
=
69(m)
答:电视塔的高度为
69
m.
如图,在
△ABD
中,∠ACB
=
45°,∠D
=
30°,AB⊥BD
,若
CD
=
10
cm,求
AB
.
练习
A
B
C
D
解
设
AB
=
x
cm.
在
Rt△ACB
中,
∵∠
ACB
=
45°,∴CB
=
AB.
在
Rt△ACD
中,
∵∠D
=
30°,
A
B
C
D
tan
∠ADB
=
=
即
解方程,得
x
=
5(
+
1).
例
5
如图一船以
20
n
mile/h
的速度向东航行,在
A处测得灯塔
C
在北偏东
60°的方向上,继续航行
1
h
到达B
处,再测得灯塔
C
在北偏东30°的方向上.
已知灯塔
C
四周
10
n
mile
内有暗礁,问这船继续向东航行是否安全?
东
北
A
B
30°
60°
C
取决于灯塔
C
到
AB航线的距离是否大于
10
n
mile.
东
北
A
B
D
30°
60°
C
解
过点
C
作
CD⊥AB
于点
D,设
CD
=
x
n
mile.
在
Rt△ACD
中,AD
=
=
在
Rt△BCD
中,
BD
=
=
东
北
A
B
D
30°
60°
C
由
AB
=
AD
–
BD,得
AB
=
–
=
20,
解方程,得
x
=
>
10.
答:这船继续向东航行时安全的.
随堂演练
1.
如图,某直升机于空中
A
处测得正前方地面控制点
C
的俯角为
30°;若航向不变,直升机继续向前飞行
1
000
m
至
B
处,测得地面控制点
C
的俯角为
45°.求直升机再向前飞行多远,与地面控制点
C的距离最近(结果保留根号).
C
B
A
45°
30°
C
B
A
45°
30°
解
过点
C
作
CD⊥AB
于点
D.
设
BD
=
x
n
mile.
D
在
Rt△BCD
中,tan
45°=
∴CD
=
BD
·
tan
45°=
x.
在
Rt△ACD
中,
tan
30°=
∴
AD
=
C
B
A
45°
30°
D
由
AB
=
AD
–
BD,得
AB
=
–
x
=
1
000,
解方程得
x
=
2.
一船向东航行,上午
9:00
到达灯塔
C
的西南方向
60
n
mile
的
A
处,上午
10:00
到达灯塔
C
的正南的
B
处.
(1)画出示意图;
(2)求这船的航行速度
(结果保留根号).
东
北
A
B
45°
C
东
北
A
B
45°
C
(2)sin
45°=
AB
=
AC
·
sin
45°
=
60×
=
(n
mile)
船航行的速度
=
÷1
=
(n
mile
/
h)
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
第3课时
解决双直角三角形问题
23.2
解直角三角形及其应用
沪科版
九年级数学上册
教学课件
学习目标
【知识与技能】
比较熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
【过程与方法】
通过学习进一步掌握解直角三角形的方法.
【情感态度】
培养学生把实际问题转化为数学问题的能力.
【教学重点】
应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
【教学难点】
选用恰当的直角三角形,解题思路分析.
新课导入
例
4
解决本章引言所提问题.
如图,某校九年级学生要测量当地电视塔的高度
AB,因为不能直接到达塔底
B
处,他们采用在发射台院外与电视塔底
B
成一直线的
CD
两处地面上,
A
B
B1
C
D
C1
D1
30°
45°
用测角器测得电视塔顶部
A
的仰角分别为
45°和
30°,同时量得
CD
为
50
m.
已知测角器高为
1
m,问电视塔的高度为多少米?(精确到
1
m)
A
B
B1
C
D
C1
D1
30°
45°
新课探究
A
B
B1
C
D
C1
D1
30°
45°
解
设
AB1
=
x
m.
在
Rt△AC1B1
中,由∠AC1B1
=
45°,得
C1B1
=
AB1.
在
Rt△AD1B1
中,由∠AD1B1
=
30°,
得
tan∠AD1B1
=
=
A
B
B1
C
D
C1
D1
30°
45°
即
解方程,得
x
=
25(
+
1)≈
68.
∴
AB
=
AB1
+
BB1
≈
68
+
1
=
69(m)
答:电视塔的高度为
69
m.
如图,在
△ABD
中,∠ACB
=
45°,∠D
=
30°,AB⊥BD
,若
CD
=
10
cm,求
AB
.
练习
A
B
C
D
解
设
AB
=
x
cm.
在
Rt△ACB
中,
∵∠
ACB
=
45°,∴CB
=
AB.
在
Rt△ACD
中,
∵∠D
=
30°,
A
B
C
D
tan
∠ADB
=
=
即
解方程,得
x
=
5(
+
1).
例
5
如图一船以
20
n
mile/h
的速度向东航行,在
A处测得灯塔
C
在北偏东
60°的方向上,继续航行
1
h
到达B
处,再测得灯塔
C
在北偏东30°的方向上.
已知灯塔
C
四周
10
n
mile
内有暗礁,问这船继续向东航行是否安全?
东
北
A
B
30°
60°
C
取决于灯塔
C
到
AB航线的距离是否大于
10
n
mile.
东
北
A
B
D
30°
60°
C
解
过点
C
作
CD⊥AB
于点
D,设
CD
=
x
n
mile.
在
Rt△ACD
中,AD
=
=
在
Rt△BCD
中,
BD
=
=
东
北
A
B
D
30°
60°
C
由
AB
=
AD
–
BD,得
AB
=
–
=
20,
解方程,得
x
=
>
10.
答:这船继续向东航行时安全的.
随堂演练
1.
如图,某直升机于空中
A
处测得正前方地面控制点
C
的俯角为
30°;若航向不变,直升机继续向前飞行
1
000
m
至
B
处,测得地面控制点
C
的俯角为
45°.求直升机再向前飞行多远,与地面控制点
C的距离最近(结果保留根号).
C
B
A
45°
30°
C
B
A
45°
30°
解
过点
C
作
CD⊥AB
于点
D.
设
BD
=
x
n
mile.
D
在
Rt△BCD
中,tan
45°=
∴CD
=
BD
·
tan
45°=
x.
在
Rt△ACD
中,
tan
30°=
∴
AD
=
C
B
A
45°
30°
D
由
AB
=
AD
–
BD,得
AB
=
–
x
=
1
000,
解方程得
x
=
2.
一船向东航行,上午
9:00
到达灯塔
C
的西南方向
60
n
mile
的
A
处,上午
10:00
到达灯塔
C
的正南的
B
处.
(1)画出示意图;
(2)求这船的航行速度
(结果保留根号).
东
北
A
B
45°
C
东
北
A
B
45°
C
(2)sin
45°=
AB
=
AC
·
sin
45°
=
60×
=
(n
mile)
船航行的速度
=
÷1
=
(n
mile
/
h)
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
