沪科版九年级数学上册 第23章 解直角三角形 23.2 解直角三角形及其应用 第4课时 坡度问题及平面直角坐标系中直线与x轴的夹角 上课课件
文档属性
| 名称 | 沪科版九年级数学上册 第23章 解直角三角形 23.2 解直角三角形及其应用 第4课时 坡度问题及平面直角坐标系中直线与x轴的夹角 上课课件 |  | |
| 格式 | zip | ||
| 文件大小 | 424.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 12:42:00 | ||
图片预览




文档简介
(共22张PPT)
第4课时
坡度问题及平面直角坐标系中
直线与
x
轴的夹角
23.2
解直角三角形及其应用
沪科版
九年级数学上册
教学课件
学习目标
【知识与技能】
1.了解测量中坡度、坡角的概念;
2.掌握坡度与坡角的关系,能利用解直角三角形的知识,解决与坡度有关的实际问题.
【过程与方法】
通过对例题的学习,使学生能够利用所学知识解决实际问题.
【情感态度】
进一步培养学生把实际问题转化为数学问题的能力.
【教学重点】
能利用解直角三角形的知识,解决与坡度、与弧长有关的实际问题.
【教学难点】
能利用解直角三角形的知识,解决与坡度的有关的实际问题.
新课导入
例
6
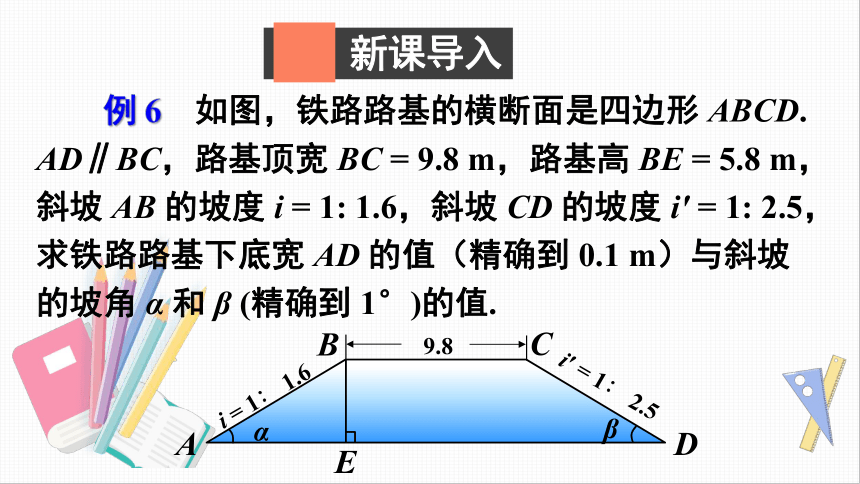
如图,铁路路基的横断面是四边形
ABCD.
AD∥BC,路基顶宽
BC
=
9.8
m,路基高
BE
=
5.8
m,斜坡
AB
的坡度
i
=
1:
1.6,斜坡
CD
的坡度
i′
=
1:
2.5,求铁路路基下底宽
AD
的值(精确到
0.1
m)与斜坡的坡角
α
和
β
(精确到
1°)的值.
A
D
E
B
C
α
β
i
=
1∶
1.6
i′
=
1∶
2.5
9.8
A
D
E
B
C
α
β
i
=
1∶
1.6
i′
=
1∶
2.5
9.8
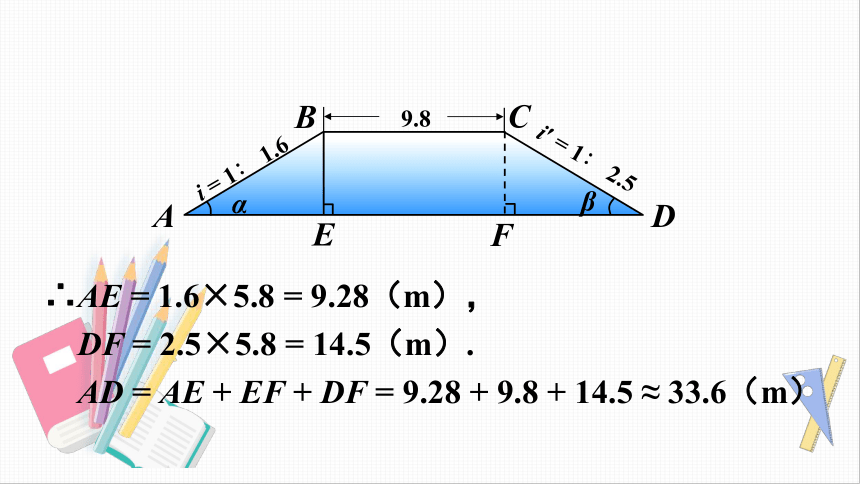
解
过点
C
作
CF
⊥AD
于点
F,得
CF
=
BE,EF
=
BC,∠A
=
α,∠D
=
β.
F
∵
BE
=
5.8
m,
,
,
新课探究
A
D
E
B
C
α
β
i
=
1∶
1.6
i′
=
1∶
2.5
9.8
F
∴AE
=
1.6×5.8
=
9.28(m),
DF
=
2.5×5.8
=
14.5(m).
AD
=
AE
+
EF
+
DF
=
9.28
+
9.8
+
14.5
≈
33.6(m)
A
D
E
B
C
α
β
i
=
1∶
1.6
i′
=
1∶
2.5
9.8
F
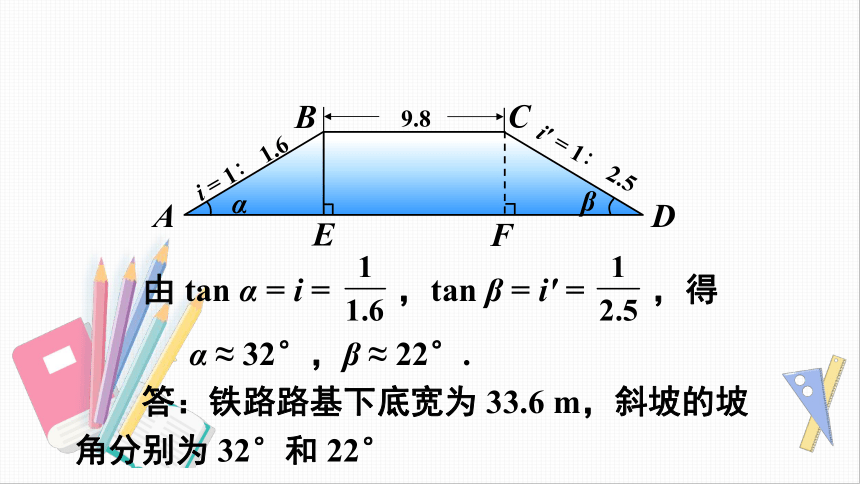
由
tan
α
=
i
=
,tan
β
=
i′
=
,得
α
≈
32°,β
≈
22°.
答:铁路路基下底宽为
33.6
m,斜坡的坡角分别为
32°和
22°
练习
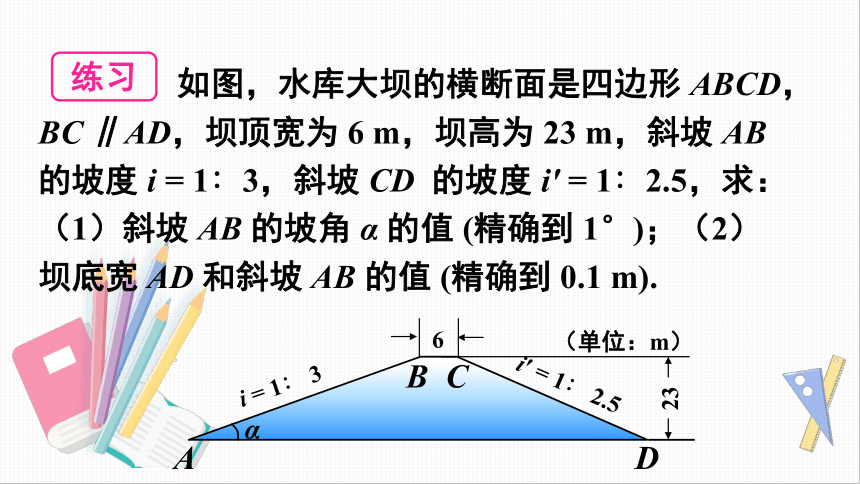
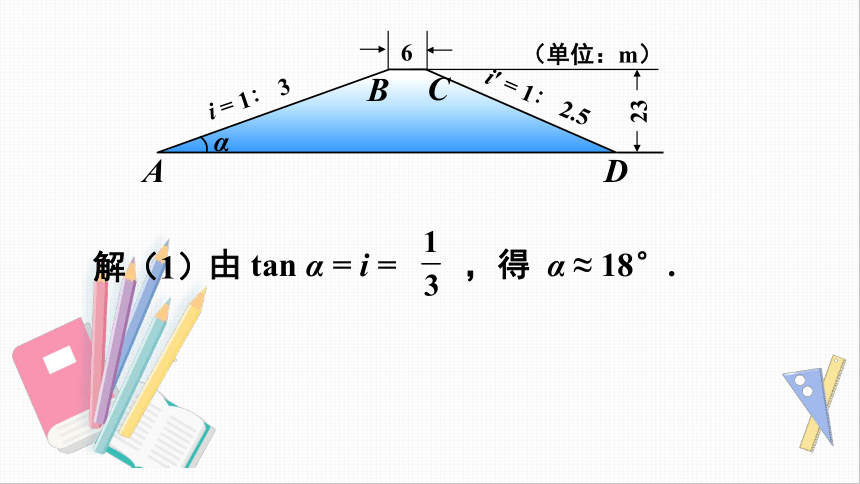
如图,水库大坝的横断面是四边形
ABCD,BC
∥AD,坝顶宽为
6
m,坝高为
23
m,斜坡
AB
的坡度
i
=
1∶3,斜坡
CD
的坡度
i′
=
1∶2.5,求:(1)斜坡
AB
的坡角
α
的值
(精确到
1°);(2)坝底宽
AD
和斜坡
AB
的值
(精确到
0.1
m).
A
D
B
C
α
i
=
1∶
3
i′
=
1∶
2.5
23
(单位:m)
6
A
D
B
C
α
i
=
1∶
3
i′
=
1∶
2.5
23
(单位:m)
6
由
tan
α
=
i
=
,得
α
≈
18°.
解(1)
A
D
B
C
α
i
=
1∶
3
i′
=
1∶
2.5
23
(单位:m)
6
E
F
(2)过点
B
作
BE
⊥AD
于点
E,过点
C
作
CF
⊥AD
于点
F,得
BE
=
CF
=
23
m,BC
=
EF
=
6
m.
∵
∴AE
=
3×23
=
69(m),
DF
=
2.5×23
=
57.5(m).
AD
=
AE
+
EF
+
DF
=
69
+
6
+
57.5
=
132.5(m)
A
D
B
C
α
i
=
1∶
3
i′
=
1∶
2.5
23
(单位:m)
6
E
F
∴
AB
=
=
≈
72.7(m)
例
7
已知:在直线
y
=
kx
+
b
上有任意两点
P1(x1,y1),P2(x2,y2),这条直线向上方向与
x
轴正方向所夹的锐角为
α.
求证:tan
α
=
=
k.
证明
由
α
是锐角,可知直线
y
=
kx
+
b
是上升的,即函数
y
=
kx
+
b
的值随
x
值的增大而增大.
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
如图,设
x1<
x2,则
y1<y2.
过点
P1,P2
作
x
轴的垂线,垂足分别为
Q1,
Q2,再过点
P1
作
x
轴的平行线P1R
交
P2Q2
于点
R,得
∠P2P1R
=
α.
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
∵
P1,P2
都在直线
y
=
kx
+
b上,
∴
y1
=
kx1
+
b,
①
y2
=
kx2
+
b.
②
由
②
–
①,得
在△P2P1R
中,
tan
α
=
=
=
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
y2
–
y1
=
k(x2
–
x1)
∴
k
=
.
即
tan
α
=
=
k.
练习
求直线
y
=
x
–
5
的正方向与
x
轴正方向所夹的锐角.
解
设这个锐角为
α,则
tan
α
=
∴
α
=
60°.
随堂演练
1.
如图,燕尾槽的横断面是四边形
ABCD,AD∥BC,其中
∠B
=
∠C
=
55°,外口宽
AD
=
180
mm,燕尾槽的深度
AE
=
70
mm,求它的里口宽
BC
的值(精确到
1
mm).
A
B
C
D
E
A
B
C
D
E
解
过点
D
作
DF
⊥BC
于点
F,
∴AD
=
EF,BE
=
CF.
F
tan
B
=
,∴
BE
=
=
≈
49(mm)
∴
BC
=
BE
+
EF
+
FC
≈
49
+
180
+
49
≈
278(mm)
2.
分别求直线
y
=
x
+
2
的向上方向与
x
轴正方向和
y
轴正方向所夹的锐角。
解
这条直线向上方向与
x
轴正方向所夹的锐角为
α,与
y
轴正方向所夹的锐角为
β.
则
tan
α
=
,α
=
30°,β
=
60°.
3.
如图,已知直线
AB
与
x
轴,y
轴分别相交于
A、B
两点,它的解析式为
,角
α
的一边为
OA,另一边为
OP⊥AB
于
P,求cos
α
的值.
A
B
O
P
α
解
由题意得
tan
A
=
,∴∠A
=
30°,
∠B
=
60°,∠α
=
∠B
=
60°.
∴cos
α
=
.
A
B
O
P
α
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
第4课时
坡度问题及平面直角坐标系中
直线与
x
轴的夹角
23.2
解直角三角形及其应用
沪科版
九年级数学上册
教学课件
学习目标
【知识与技能】
1.了解测量中坡度、坡角的概念;
2.掌握坡度与坡角的关系,能利用解直角三角形的知识,解决与坡度有关的实际问题.
【过程与方法】
通过对例题的学习,使学生能够利用所学知识解决实际问题.
【情感态度】
进一步培养学生把实际问题转化为数学问题的能力.
【教学重点】
能利用解直角三角形的知识,解决与坡度、与弧长有关的实际问题.
【教学难点】
能利用解直角三角形的知识,解决与坡度的有关的实际问题.
新课导入
例
6
如图,铁路路基的横断面是四边形
ABCD.
AD∥BC,路基顶宽
BC
=
9.8
m,路基高
BE
=
5.8
m,斜坡
AB
的坡度
i
=
1:
1.6,斜坡
CD
的坡度
i′
=
1:
2.5,求铁路路基下底宽
AD
的值(精确到
0.1
m)与斜坡的坡角
α
和
β
(精确到
1°)的值.
A
D
E
B
C
α
β
i
=
1∶
1.6
i′
=
1∶
2.5
9.8
A
D
E
B
C
α
β
i
=
1∶
1.6
i′
=
1∶
2.5
9.8
解
过点
C
作
CF
⊥AD
于点
F,得
CF
=
BE,EF
=
BC,∠A
=
α,∠D
=
β.
F
∵
BE
=
5.8
m,
,
,
新课探究
A
D
E
B
C
α
β
i
=
1∶
1.6
i′
=
1∶
2.5
9.8
F
∴AE
=
1.6×5.8
=
9.28(m),
DF
=
2.5×5.8
=
14.5(m).
AD
=
AE
+
EF
+
DF
=
9.28
+
9.8
+
14.5
≈
33.6(m)
A
D
E
B
C
α
β
i
=
1∶
1.6
i′
=
1∶
2.5
9.8
F
由
tan
α
=
i
=
,tan
β
=
i′
=
,得
α
≈
32°,β
≈
22°.
答:铁路路基下底宽为
33.6
m,斜坡的坡角分别为
32°和
22°
练习
如图,水库大坝的横断面是四边形
ABCD,BC
∥AD,坝顶宽为
6
m,坝高为
23
m,斜坡
AB
的坡度
i
=
1∶3,斜坡
CD
的坡度
i′
=
1∶2.5,求:(1)斜坡
AB
的坡角
α
的值
(精确到
1°);(2)坝底宽
AD
和斜坡
AB
的值
(精确到
0.1
m).
A
D
B
C
α
i
=
1∶
3
i′
=
1∶
2.5
23
(单位:m)
6
A
D
B
C
α
i
=
1∶
3
i′
=
1∶
2.5
23
(单位:m)
6
由
tan
α
=
i
=
,得
α
≈
18°.
解(1)
A
D
B
C
α
i
=
1∶
3
i′
=
1∶
2.5
23
(单位:m)
6
E
F
(2)过点
B
作
BE
⊥AD
于点
E,过点
C
作
CF
⊥AD
于点
F,得
BE
=
CF
=
23
m,BC
=
EF
=
6
m.
∵
∴AE
=
3×23
=
69(m),
DF
=
2.5×23
=
57.5(m).
AD
=
AE
+
EF
+
DF
=
69
+
6
+
57.5
=
132.5(m)
A
D
B
C
α
i
=
1∶
3
i′
=
1∶
2.5
23
(单位:m)
6
E
F
∴
AB
=
=
≈
72.7(m)
例
7
已知:在直线
y
=
kx
+
b
上有任意两点
P1(x1,y1),P2(x2,y2),这条直线向上方向与
x
轴正方向所夹的锐角为
α.
求证:tan
α
=
=
k.
证明
由
α
是锐角,可知直线
y
=
kx
+
b
是上升的,即函数
y
=
kx
+
b
的值随
x
值的增大而增大.
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
如图,设
x1<
x2,则
y1<y2.
过点
P1,P2
作
x
轴的垂线,垂足分别为
Q1,
Q2,再过点
P1
作
x
轴的平行线P1R
交
P2Q2
于点
R,得
∠P2P1R
=
α.
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
∵
P1,P2
都在直线
y
=
kx
+
b上,
∴
y1
=
kx1
+
b,
①
y2
=
kx2
+
b.
②
由
②
–
①,得
在△P2P1R
中,
tan
α
=
=
=
x
y
O
α
Q1
Q2
α
R
P1(x1,y1)
P2(x2,y2)
y2
–
y1
=
k(x2
–
x1)
∴
k
=
.
即
tan
α
=
=
k.
练习
求直线
y
=
x
–
5
的正方向与
x
轴正方向所夹的锐角.
解
设这个锐角为
α,则
tan
α
=
∴
α
=
60°.
随堂演练
1.
如图,燕尾槽的横断面是四边形
ABCD,AD∥BC,其中
∠B
=
∠C
=
55°,外口宽
AD
=
180
mm,燕尾槽的深度
AE
=
70
mm,求它的里口宽
BC
的值(精确到
1
mm).
A
B
C
D
E
A
B
C
D
E
解
过点
D
作
DF
⊥BC
于点
F,
∴AD
=
EF,BE
=
CF.
F
tan
B
=
,∴
BE
=
=
≈
49(mm)
∴
BC
=
BE
+
EF
+
FC
≈
49
+
180
+
49
≈
278(mm)
2.
分别求直线
y
=
x
+
2
的向上方向与
x
轴正方向和
y
轴正方向所夹的锐角。
解
这条直线向上方向与
x
轴正方向所夹的锐角为
α,与
y
轴正方向所夹的锐角为
β.
则
tan
α
=
,α
=
30°,β
=
60°.
3.
如图,已知直线
AB
与
x
轴,y
轴分别相交于
A、B
两点,它的解析式为
,角
α
的一边为
OA,另一边为
OP⊥AB
于
P,求cos
α
的值.
A
B
O
P
α
解
由题意得
tan
A
=
,∴∠A
=
30°,
∠B
=
60°,∠α
=
∠B
=
60°.
∴cos
α
=
.
A
B
O
P
α
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
