沪科版九年级数学上册 第23章 解直角三角形 章末复习 上课课件(共18张PPT)
文档属性
| 名称 | 沪科版九年级数学上册 第23章 解直角三角形 章末复习 上课课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 596.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 17:02:59 | ||
图片预览






文档简介
(共18张PPT)
沪科版
九年级数学上册
教学课件
章末复习
第23章
解直角三角形
学习目标
【知识与技能】
1.了解锐角三角函数的概念,记忆30°、45°、60°的正弦、余弦和正切的函数值.
2.能够正确地使用计算器,由已知锐角的度数求出它的三角函数值,由已知的三角函数值求出相应的锐角的度数.
3.会用解直角三角形的有关知识解决简单的实际问题.
【过程与方法】
通过锐角三角函数的学习,进一步认识函数,体会函数的变化与对应的思想.
【情感态度】
通过解直角三角形的学习,体会数学在解决实际问题中的作用.
【教学重点】
会用解直角三角形的有关知识解决简单的实际问题.
【教学难点】
会用解直角三角形的有关知识解决简单的实际问题.
知识梳理
如图,在
Rt△ABC
中,我们把锐角
A
的对边与邻边的比叫做∠A
的正切,记作tanA,
A
B
C
∠A
的邻边
b
∠A
的对边
a
斜边
c
tan
A
=
=
=
∠A
的对边
∠A
的邻边
BC
AC
a
b
即
A
B
C
∠A
的邻边
b
∠A
的对边
a
斜边
c
如图,在
Rt△ABC
中.
我们把锐角
A
的对边与斜边的比叫做∠A
的正弦,记作
sinA,即
sin
A
=
=
=
∠A
的对边
斜边
BC
AB
a
c
A
B
C
∠A
的邻边
b
∠A
的对边
a
斜边
c
同理,我们把锐角
A
的邻边与斜边的比叫做∠A
的余弦,记作cos
A,即
cos
A
=
=
=
∠A
的邻边
斜边
AC
AB
b
c
锐角
A
的正弦、余弦、正切都叫做锐角A
的三角函数.
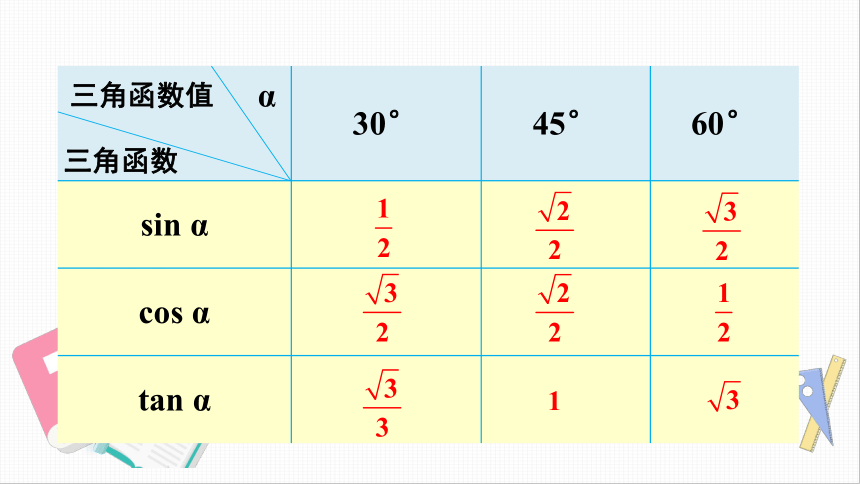
30°
45°
60°
sin
α
cos
α
tan
α
三角函数
三角函数值
α
任意一个锐角的正(余)弦的值,等于它的余角的余(正)弦的值.
在
Rt△ABC
中,∠C
=
90°,
sin2
A
+
cos2
A
=
1
tan
A
·
tan
B
=
1
如图,先按
键,再按
键,使显示器屏幕出现“DEG”,然后再按有关三角函数的键,就可以求三角函数了.
ON/C
MODE
A
C
B
a
b
c
(1)三边之间的关系
a2
+
b2
=
____;
(2)锐角之间的关系
∠A
+
∠B
=
____;
(3)边角之间的关系
sin
A
=
____,cos
A
=
____,tan
A
=
____.
c2
90°
a
c
b
c
a
b
对于锐角
B,也有类似的边角关系吗?
典例解析
1.
如图,在
Rt△ABC
中,∠C
=
90°,AB
=
10,AC
=
8,则
sin
A
等于( )
A
B
C
A.
B.
C.
D.
A
2.
如图,两根竹竿
AB
和
AD
斜靠在墙
CE上,量得
∠ABC
=
α,∠ADC
=
β,则竹竿
AB与
AD
的长度之比为( )
A.
B.
C.
D.
A
C
B
D
E
α
β
B
3.
在数学实践活动课上,老师带领同学们到附近的湿地公园测量园内雕塑的高度.
用测角仪在
A
处测得雕塑顶端点
C
的仰角为
30°,再往雕塑方向前进
4
米至
B
处,测得仰角为45°.
问:该雕塑有多高?(测角仪高度忽略不计,结果不取近似值.)
解:如图,过点
C
作
CD⊥AB,交
AB
延长线于点
D,设
CD
=
x
米,
∵∠CBD
=
45°,∠BDC
=
90°,
∴BD
=
CD
=
x
米,∵∠A
=
30°,
AD
=
AB
+
BD
=
4
+
x,
tan
A
=
,即
解得
x
=
2
+
4.
小亮在某桥附近试飞无人机,如图,为了测量无人机飞行的高度
AD,小亮通过操控器指令无人机测得桥头
B,C
的俯角分别为∠EAB
=
60°,∠EAC
=
30°,且
D,B,C
在同一水平线上.
已知桥
BC
=
30
米,求无人机飞行的高度
AD.(精确到
0.01
米.参考数据
≈
1.414,
≈
1.732)
解:∵∠EAB
=
60°,∠EAC
=
30°,
∴∠CAD
=
60°,∠BAD
=
30°,
∴CD
=
AD
·
tan∠CAD
=
AD,
BD
=
AD
·
tan∠BAD
=
AD,
∴BC
=
CD
–
BD
=
AD
=
30,
∴
AD
=
15
≈
25.98.
课后作业
1.完成课本的练习,
2.完成练习册本课时的习题.
谢谢欣赏
沪科版
九年级数学上册
教学课件
章末复习
第23章
解直角三角形
学习目标
【知识与技能】
1.了解锐角三角函数的概念,记忆30°、45°、60°的正弦、余弦和正切的函数值.
2.能够正确地使用计算器,由已知锐角的度数求出它的三角函数值,由已知的三角函数值求出相应的锐角的度数.
3.会用解直角三角形的有关知识解决简单的实际问题.
【过程与方法】
通过锐角三角函数的学习,进一步认识函数,体会函数的变化与对应的思想.
【情感态度】
通过解直角三角形的学习,体会数学在解决实际问题中的作用.
【教学重点】
会用解直角三角形的有关知识解决简单的实际问题.
【教学难点】
会用解直角三角形的有关知识解决简单的实际问题.
知识梳理
如图,在
Rt△ABC
中,我们把锐角
A
的对边与邻边的比叫做∠A
的正切,记作tanA,
A
B
C
∠A
的邻边
b
∠A
的对边
a
斜边
c
tan
A
=
=
=
∠A
的对边
∠A
的邻边
BC
AC
a
b
即
A
B
C
∠A
的邻边
b
∠A
的对边
a
斜边
c
如图,在
Rt△ABC
中.
我们把锐角
A
的对边与斜边的比叫做∠A
的正弦,记作
sinA,即
sin
A
=
=
=
∠A
的对边
斜边
BC
AB
a
c
A
B
C
∠A
的邻边
b
∠A
的对边
a
斜边
c
同理,我们把锐角
A
的邻边与斜边的比叫做∠A
的余弦,记作cos
A,即
cos
A
=
=
=
∠A
的邻边
斜边
AC
AB
b
c
锐角
A
的正弦、余弦、正切都叫做锐角A
的三角函数.
30°
45°
60°
sin
α
cos
α
tan
α
三角函数
三角函数值
α
任意一个锐角的正(余)弦的值,等于它的余角的余(正)弦的值.
在
Rt△ABC
中,∠C
=
90°,
sin2
A
+
cos2
A
=
1
tan
A
·
tan
B
=
1
如图,先按
键,再按
键,使显示器屏幕出现“DEG”,然后再按有关三角函数的键,就可以求三角函数了.
ON/C
MODE
A
C
B
a
b
c
(1)三边之间的关系
a2
+
b2
=
____;
(2)锐角之间的关系
∠A
+
∠B
=
____;
(3)边角之间的关系
sin
A
=
____,cos
A
=
____,tan
A
=
____.
c2
90°
a
c
b
c
a
b
对于锐角
B,也有类似的边角关系吗?
典例解析
1.
如图,在
Rt△ABC
中,∠C
=
90°,AB
=
10,AC
=
8,则
sin
A
等于( )
A
B
C
A.
B.
C.
D.
A
2.
如图,两根竹竿
AB
和
AD
斜靠在墙
CE上,量得
∠ABC
=
α,∠ADC
=
β,则竹竿
AB与
AD
的长度之比为( )
A.
B.
C.
D.
A
C
B
D
E
α
β
B
3.
在数学实践活动课上,老师带领同学们到附近的湿地公园测量园内雕塑的高度.
用测角仪在
A
处测得雕塑顶端点
C
的仰角为
30°,再往雕塑方向前进
4
米至
B
处,测得仰角为45°.
问:该雕塑有多高?(测角仪高度忽略不计,结果不取近似值.)
解:如图,过点
C
作
CD⊥AB,交
AB
延长线于点
D,设
CD
=
x
米,
∵∠CBD
=
45°,∠BDC
=
90°,
∴BD
=
CD
=
x
米,∵∠A
=
30°,
AD
=
AB
+
BD
=
4
+
x,
tan
A
=
,即
解得
x
=
2
+
4.
小亮在某桥附近试飞无人机,如图,为了测量无人机飞行的高度
AD,小亮通过操控器指令无人机测得桥头
B,C
的俯角分别为∠EAB
=
60°,∠EAC
=
30°,且
D,B,C
在同一水平线上.
已知桥
BC
=
30
米,求无人机飞行的高度
AD.(精确到
0.01
米.参考数据
≈
1.414,
≈
1.732)
解:∵∠EAB
=
60°,∠EAC
=
30°,
∴∠CAD
=
60°,∠BAD
=
30°,
∴CD
=
AD
·
tan∠CAD
=
AD,
BD
=
AD
·
tan∠BAD
=
AD,
∴BC
=
CD
–
BD
=
AD
=
30,
∴
AD
=
15
≈
25.98.
课后作业
1.完成课本的练习,
2.完成练习册本课时的习题.
谢谢欣赏
