八年级数学1-2三角形全等的条件(一)
文档属性
| 名称 | 八年级数学1-2三角形全等的条件(一) |

|
|
| 格式 | zip | ||
| 文件大小 | 75.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-18 21:04:19 | ||
图片预览

文档简介
三角形全等的条件(一)
教学目标
1、使学生经历探索三角形全等的条件的过程,体验用操作、归纳得出数学结论的过程。
2、掌握三角形全等的“边边边”条件,能初步应用此条件判定两个三角形全等,了解三角形的稳定性。
教学重难点
重点:指导学生分析问题,寻找判定三角形全等的“边边边”条件。
难点:探究三角形全等的条件
教学过程
一、复习引入
【活动1】
1、全等三角形的定义
2、全等三角形的性质
如图,若△ABC≌△A′B′C′,点A与点A′,点B与B′是对应顶点;可得出:
AB=A′B′ AC=A′C′ BC=B′C′
∠A=∠A′ ∠B=∠B′ ∠C=∠C′
3、反之若△ABC与△A′B′C′满足上述六个条件就能保证两个三角形全等吗?
4、判断两个三角形全等,以我们目前的知识有什么方法呢?是不是一定要满足六个条件呢?满足上述六个条件中的一部分是否就能保证两个三角形全等呢?今天我们就一起来探讨一下这个问题。
二、探究新知
【活动2】
1、△ABC与△A′B′C′满足上述条件中的一个,能保证两个三角形全等吗?满足六个条件中的两个呢?
2、让学生按照下面给出条件作出三角形。
① 一个角为30°的三角形
② 一条边为5cm的三角形
③ 两条边分别为4cm、6cm的三角形
④ 一个角为30°,一条边为6cm的三角形
⑤ 两个角分别为30°、60°的三角形
通过所画的三角形,请同学们与周围同学所画的对应的三角形比一比(剪下),它们全等吗?
1)只给定一条边时:
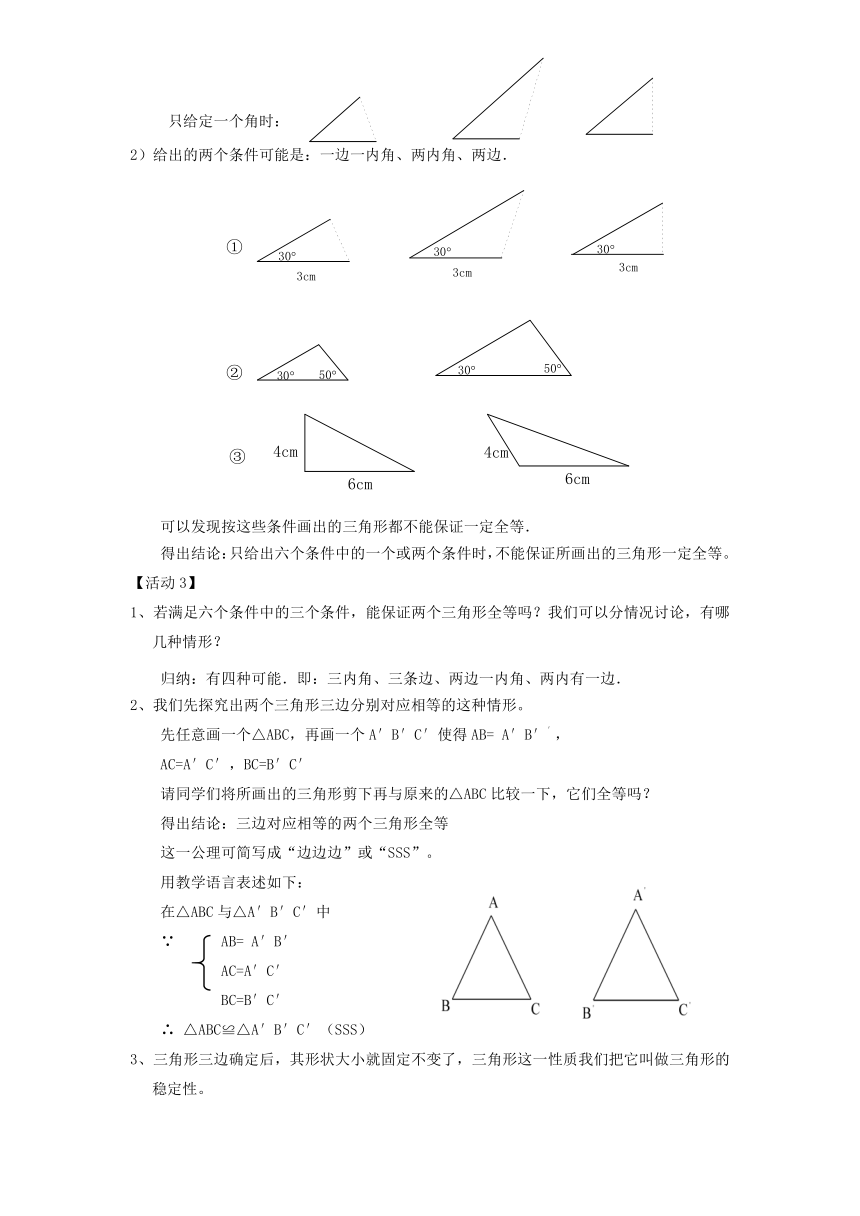
只给定一个角时:
2)给出的两个条件可能是:一边一内角、两内角、两边.
可以发现按这些条件画出的三角形都不能保证一定全等.
得出结论:只给出六个条件中的一个或两个条件时,不能保证所画出的三角形一定全等。
【活动3】
1、若满足六个条件中的三个条件,能保证两个三角形全等吗?我们可以分情况讨论,有哪几种情形?
归纳:有四种可能.即:三内角、三条边、两边一内角、两内有一边.
2、我们先探究出两个三角形三边分别对应相等的这种情形。
先任意画一个△ABC,再画一个A′B′C′使得AB= A′B′′,
AC=A′C′,BC=B′C′
请同学们将所画出的三角形剪下再与原来的△ABC比较一下,它们全等吗?
得出结论:三边对应相等的两个三角形全等
这一公理可简写成“边边边”或“SSS”。
用教学语言表述如下:
在△ABC与△A′B′C′中
∵ AB= A′B′
AC=A′C′
BC=B′C′
∴ △ABC≌△A′B′C′(SSS)
3、三角形三边确定后,其形状大小就固定不变了,三角形这一性质我们把它叫做三角形的稳定性。
三、应用新知
例1、如下图,A、C、B、D在同一条直线上,AC=BD,AM=CN,BM=DN,证明:△ABM≌△CDN.
分析:要证△ABM≌△CDN,可看这两个三角形的三条边是否相等,由题设AM=CN,BM=DN,故只需判断第三边AB=CD即可,由于AC=BD,故可得AB=CD.
证明:∵AC=BD,
∴AC+CB=CB+BD即AB=CD
在△ABM与△CDN中
所以△ABM≌△CDN.
小结:像这种判断两个三角形全等的推理过程叫证明三角形全等。
证明:由条件出发经过一步步的推理最后推出结论正确的过程。
例2、如下图,AC、BD相交于O,且AB=DC,AC=BD,则∠A=∠D,为什么?
分析:要说明∠A=∠D,可说明它们所在的△ABO和△DCO全等,而只有AB=DC这一组对边相等,不具备条件,难以确定它们是否全等.于是需转换思维角度,由于∠A、∠D又在△ABC和△DCB中,由题设易知这两个三角形的三条对应边相等,因此这两个三角形全等,故不难推证∠A=∠D.
例3、如下图,△ABC和△DEF是全等三角形,若AB=DE,∠B=50°,∠C=70°,∠E =50°,求∠D的度数.
例4、如下图,A在线段DE上,△AEC≌△BDA.
(1)若∠AEC=90°,则∠BAC也等于90°吗?为什么?
(2)若EC=1,EA∶AD=3∶1,求ED的长度.
如图△ABC是一个钢架,AB= AC,AD是连接点A与BC中点D的支架,
求证①△ABD≌△ACD ②AD⊥BC
练习①. 如图:如果AB=CD,AD=BC,那么△ABC≌△CDA,其根据是 。
②. 如图:AB=CB,BE=BD,AE=CD,请写出图中所有的全等三角形: 。
四、课后作业
1.下列判断两个三角形全等的条件中,正确的是( )
A. 一条边对应相等 B. 两条边对应相等 C. 三个角对应相等 D. 三条边对应相等
2.如图,在①AB=AC ②AD=AE ③∠B=∠C ④BD=CE四个条件中,能证明△ABD与△ACE全等的条件顺序是( )
A. ① ② ③ B. ② ③ ④ C. ① ② ④ D. ③ ② ④
3.如图,在△ABC中,AB=AC,D、E两点在BC上,且有AD=AE,
BD=CE,若∠BAD=30°∠DAE=50°,则∠BAC的度数为( )
A.130° B. 120° C.110° D.100°
4.如图, AB= AC,BE=CD,要使△ABE≌△ACD,依据SSS,则还需添加条件
5.如图,AB=ED,AC=EC,C是BD的中点,若∠A=36°,则∠E=
第2题图 第3题图 第4题图 第5题图 第6题图
6.如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中全等的三角形共有 对.
7.在平面直角坐标系中有两点A(4,0)、B(0,2),如果点C在坐标平面内,当点C的坐标为
或 时,由点B、O、C组成的三角形与△AOB全等。
8. 如图四边形ABCD中,AB=CD,AD=BC,你能把四边形ABCD分成一对全等的三角形吗 你有几种方法 你能证明你的方法吗 试一试. 你能把它分成两对全等的三角形吗 试试看.
9、如图,已知AC=AD,BC=BD,求证:∠1=∠2.
10.如图,AD=CB,E、F是AC上两动点,且有DE=BF,(1)若E、F运动至如图①所示的位置,且有AF=CE,求证:△ADE≌△CBF (2)若E、F运动至如图②所示的位置,仍有AF=CE,那么△ADE≌△CBF还成立吗?为什么?(3)若E、F不重合,AD和CB平行吗?说明理由。
11、如下图,在△ABC中,D、E分别是AC、BC上的点,若△ADB≌△EDB≌△EDC,求∠C的度数。
教学目标
1、使学生经历探索三角形全等的条件的过程,体验用操作、归纳得出数学结论的过程。
2、掌握三角形全等的“边边边”条件,能初步应用此条件判定两个三角形全等,了解三角形的稳定性。
教学重难点
重点:指导学生分析问题,寻找判定三角形全等的“边边边”条件。
难点:探究三角形全等的条件
教学过程
一、复习引入
【活动1】
1、全等三角形的定义
2、全等三角形的性质
如图,若△ABC≌△A′B′C′,点A与点A′,点B与B′是对应顶点;可得出:
AB=A′B′ AC=A′C′ BC=B′C′
∠A=∠A′ ∠B=∠B′ ∠C=∠C′
3、反之若△ABC与△A′B′C′满足上述六个条件就能保证两个三角形全等吗?
4、判断两个三角形全等,以我们目前的知识有什么方法呢?是不是一定要满足六个条件呢?满足上述六个条件中的一部分是否就能保证两个三角形全等呢?今天我们就一起来探讨一下这个问题。
二、探究新知
【活动2】
1、△ABC与△A′B′C′满足上述条件中的一个,能保证两个三角形全等吗?满足六个条件中的两个呢?
2、让学生按照下面给出条件作出三角形。
① 一个角为30°的三角形
② 一条边为5cm的三角形
③ 两条边分别为4cm、6cm的三角形
④ 一个角为30°,一条边为6cm的三角形
⑤ 两个角分别为30°、60°的三角形
通过所画的三角形,请同学们与周围同学所画的对应的三角形比一比(剪下),它们全等吗?
1)只给定一条边时:
只给定一个角时:
2)给出的两个条件可能是:一边一内角、两内角、两边.
可以发现按这些条件画出的三角形都不能保证一定全等.
得出结论:只给出六个条件中的一个或两个条件时,不能保证所画出的三角形一定全等。
【活动3】
1、若满足六个条件中的三个条件,能保证两个三角形全等吗?我们可以分情况讨论,有哪几种情形?
归纳:有四种可能.即:三内角、三条边、两边一内角、两内有一边.
2、我们先探究出两个三角形三边分别对应相等的这种情形。
先任意画一个△ABC,再画一个A′B′C′使得AB= A′B′′,
AC=A′C′,BC=B′C′
请同学们将所画出的三角形剪下再与原来的△ABC比较一下,它们全等吗?
得出结论:三边对应相等的两个三角形全等
这一公理可简写成“边边边”或“SSS”。
用教学语言表述如下:
在△ABC与△A′B′C′中
∵ AB= A′B′
AC=A′C′
BC=B′C′
∴ △ABC≌△A′B′C′(SSS)
3、三角形三边确定后,其形状大小就固定不变了,三角形这一性质我们把它叫做三角形的稳定性。
三、应用新知
例1、如下图,A、C、B、D在同一条直线上,AC=BD,AM=CN,BM=DN,证明:△ABM≌△CDN.
分析:要证△ABM≌△CDN,可看这两个三角形的三条边是否相等,由题设AM=CN,BM=DN,故只需判断第三边AB=CD即可,由于AC=BD,故可得AB=CD.
证明:∵AC=BD,
∴AC+CB=CB+BD即AB=CD
在△ABM与△CDN中
所以△ABM≌△CDN.
小结:像这种判断两个三角形全等的推理过程叫证明三角形全等。
证明:由条件出发经过一步步的推理最后推出结论正确的过程。
例2、如下图,AC、BD相交于O,且AB=DC,AC=BD,则∠A=∠D,为什么?
分析:要说明∠A=∠D,可说明它们所在的△ABO和△DCO全等,而只有AB=DC这一组对边相等,不具备条件,难以确定它们是否全等.于是需转换思维角度,由于∠A、∠D又在△ABC和△DCB中,由题设易知这两个三角形的三条对应边相等,因此这两个三角形全等,故不难推证∠A=∠D.
例3、如下图,△ABC和△DEF是全等三角形,若AB=DE,∠B=50°,∠C=70°,∠E =50°,求∠D的度数.
例4、如下图,A在线段DE上,△AEC≌△BDA.
(1)若∠AEC=90°,则∠BAC也等于90°吗?为什么?
(2)若EC=1,EA∶AD=3∶1,求ED的长度.
如图△ABC是一个钢架,AB= AC,AD是连接点A与BC中点D的支架,
求证①△ABD≌△ACD ②AD⊥BC
练习①. 如图:如果AB=CD,AD=BC,那么△ABC≌△CDA,其根据是 。
②. 如图:AB=CB,BE=BD,AE=CD,请写出图中所有的全等三角形: 。
四、课后作业
1.下列判断两个三角形全等的条件中,正确的是( )
A. 一条边对应相等 B. 两条边对应相等 C. 三个角对应相等 D. 三条边对应相等
2.如图,在①AB=AC ②AD=AE ③∠B=∠C ④BD=CE四个条件中,能证明△ABD与△ACE全等的条件顺序是( )
A. ① ② ③ B. ② ③ ④ C. ① ② ④ D. ③ ② ④
3.如图,在△ABC中,AB=AC,D、E两点在BC上,且有AD=AE,
BD=CE,若∠BAD=30°∠DAE=50°,则∠BAC的度数为( )
A.130° B. 120° C.110° D.100°
4.如图, AB= AC,BE=CD,要使△ABE≌△ACD,依据SSS,则还需添加条件
5.如图,AB=ED,AC=EC,C是BD的中点,若∠A=36°,则∠E=
第2题图 第3题图 第4题图 第5题图 第6题图
6.如图,已知AB=AC,EB=EC,AE的延长线交BC于D,则图中全等的三角形共有 对.
7.在平面直角坐标系中有两点A(4,0)、B(0,2),如果点C在坐标平面内,当点C的坐标为
或 时,由点B、O、C组成的三角形与△AOB全等。
8. 如图四边形ABCD中,AB=CD,AD=BC,你能把四边形ABCD分成一对全等的三角形吗 你有几种方法 你能证明你的方法吗 试一试. 你能把它分成两对全等的三角形吗 试试看.
9、如图,已知AC=AD,BC=BD,求证:∠1=∠2.
10.如图,AD=CB,E、F是AC上两动点,且有DE=BF,(1)若E、F运动至如图①所示的位置,且有AF=CE,求证:△ADE≌△CBF (2)若E、F运动至如图②所示的位置,仍有AF=CE,那么△ADE≌△CBF还成立吗?为什么?(3)若E、F不重合,AD和CB平行吗?说明理由。
11、如下图,在△ABC中,D、E分别是AC、BC上的点,若△ADB≌△EDB≌△EDC,求∠C的度数。
