八年级数学1-5三角形全等的条件(五)
文档属性
| 名称 | 八年级数学1-5三角形全等的条件(五) |  | |
| 格式 | zip | ||
| 文件大小 | 280.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-18 21:06:02 | ||
图片预览


文档简介
三角形全等的条件(五)---直角三角形全等的判定
教学目标
1、经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2、掌握直角三角形全等的条件,并能运用其解决一些实际问题。
3、在探索直角三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理。
教学重难点
重点:运用直角三角形全等的条件解决一些实际问题。
难点:熟练运用直角三角形全等的条件解决一些实际问题。
教学过程
一.提出问题,复习旧知
1、判定两个三角形全等的方法: 、 、 、
2、如图,Rt△ABC中,直角边是 、 ,斜边是
3、如图,AB⊥BE于B,DE⊥BE于E,
(1)若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
(2)若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
(3)若AB=DE,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
(4)若AB=DE,BC=EF,AC=DF
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
问题:对于两个直角三角形还有其它的判定方法吗?
二.导入新课
(一)探索练习:(动手操作):
已知线段a ,c (aAB=c ,CB= a
1、按步骤作图:
作∠MCN=∠=90°,
在射线 CM上截取线段CB=a,
③以B 为圆心,c为半径画弧,交射线CN于点A,
④连结AB
2、与同桌重叠比较,是否重合?
3、从中你发现了什么?
斜边与一直角边对应相等的两个直角三角形全等.(HL)
小结:你能够用几种方法说明两个直角三角形全等?
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.
(二)巩固练习:
1.如图,△ABC中,AB=AC,AD是高,
则△ADB与△ADC (填“全等”或“不全等” )
根据 (用简写法)
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,
根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,
根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,
根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,
根据
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,
根据
3、判断两个直角三角形全等的方法不正确的有( )
两条直角边对应相等 (B)斜边和一锐角对应相等
(C)斜边和一条直角边对应相等 (D)两个锐角对应相等
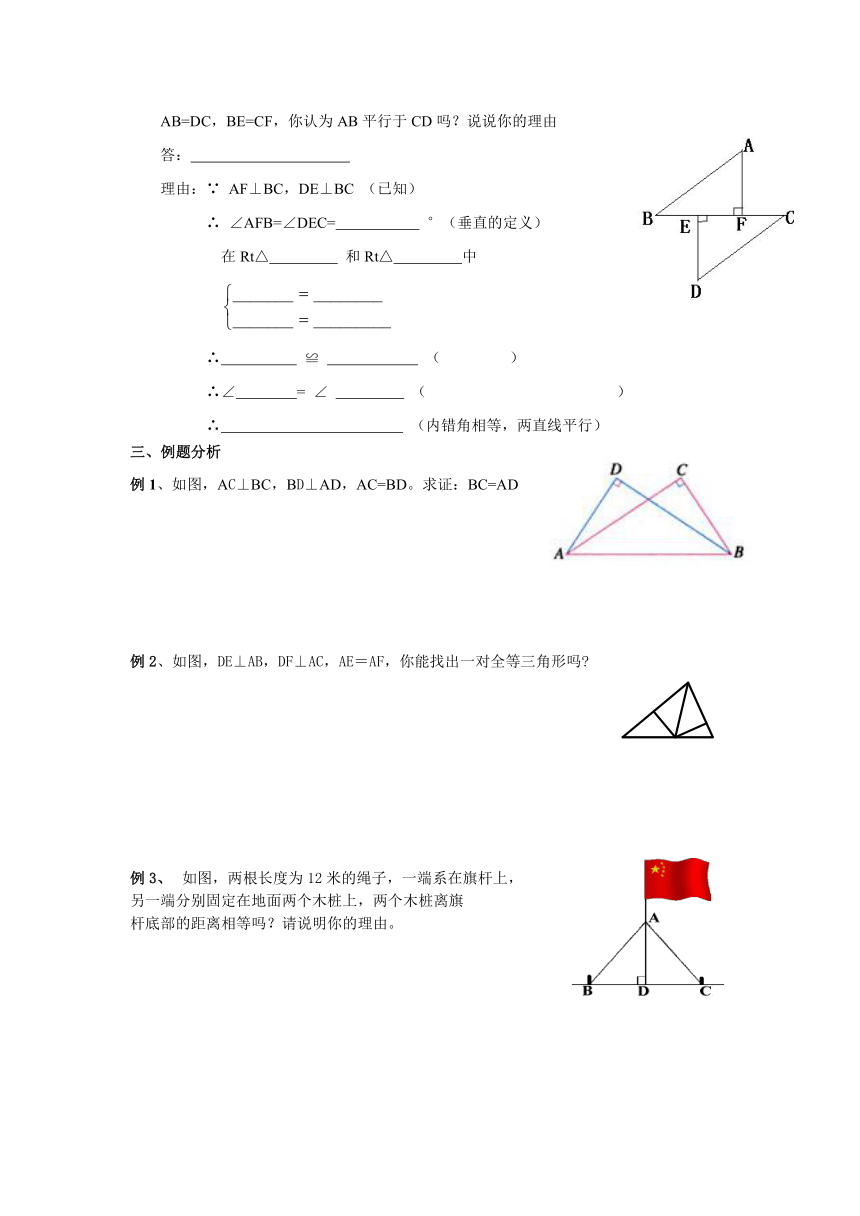
4、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:
理由:∵ AF⊥BC,DE⊥BC (已知)
∴ ∠AFB=∠DEC= °(垂直的定义)
在Rt△ 和Rt△ 中
∴ ≌ ( )
∴∠ = ∠ ( )
∴ (内错角相等,两直线平行)
三、例题分析
例1、如图,AC⊥BC,BD⊥AD,AC=BD。求证:BC=AD
例2、如图,DE⊥AB,DF⊥AC,AE=AF,你能找出一对全等三角形吗
如图,两根长度为12米的绳子,一端系在旗杆上,
另一端分别固定在地面两个木桩上,两个木桩离旗
杆底部的距离相等吗?请说明你的理由。
例4、如图,有两个长度相同的滑梯,左边滑梯的高度AC
与右边滑梯水平方向的长度DF相等,两个滑梯的倾
斜角∠ABC和∠DFE的大小有什么关系?
例5、如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF。
(1)图中有几对全等的三角形?请一一列出;
(2)选择一对你认为全等的三角形进行证明。
四、课后练习
填空题
1.判定两直角三角形全等的“HL”这种特殊方法指的是____ .
2.直角三角形全等的判定方法有_____ (用简写).
3.如图5-1,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌_____,全等的根据是_____.
图5-1
4.判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和这个角的邻边对应相等;( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等. ( )
选择题
5.下列说法正确的是 ( )
A.一直角边对应相等的两个直角三角形全等
B.斜边相等的两个直角三角形全等
C.斜边相等的两个等腰直角三角形全等
D.一边长相等的两等腰直角三角形全等
6.如图5-2,AB=AC,AD⊥ BC于D,E、F为AD上的点,则图中共有( )对全等三角形.
A.3 B.4 C.5 D.6
图5-2
解答题
7.已知:如图5-3,AB⊥BD,CD⊥BD,AD=BC.
求证:(1)AB=DC
(2)AD∥BC.
图5-3
8.已知:如图5-4,AC=BD,AD⊥AC,BC⊥BD.
求证:AD=BC;
图5-4
9.已知:如图5-5,AE⊥AB,BC⊥AB,AE=AB,ED=AC.
求证:ED⊥AC.
图5-5
10.已知:如图5-6,DE⊥AC,BF⊥AC,AD=BC,DE=BF.
求证:AB∥DC.
图5-6
11.用三角板可按下面方法画角平分线:在已知∠AOB的两边上,分别取OM=ON (如图5-7),再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB,请你说出其中的道理.
图5-7
12.(1)已知:如图5-8,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.
求证:BO=DO.
图5-8
(2)若∠AOB为锐角,其他条件不变,请画出图形并判断 (1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
a
c
C
M
N
教学目标
1、经历探索直角三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2、掌握直角三角形全等的条件,并能运用其解决一些实际问题。
3、在探索直角三角形全等条件及其运用的过程中,能够进行有条理的思考并进行简单的推理。
教学重难点
重点:运用直角三角形全等的条件解决一些实际问题。
难点:熟练运用直角三角形全等的条件解决一些实际问题。
教学过程
一.提出问题,复习旧知
1、判定两个三角形全等的方法: 、 、 、
2、如图,Rt△ABC中,直角边是 、 ,斜边是
3、如图,AB⊥BE于B,DE⊥BE于E,
(1)若∠A=∠D,AB=DE,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
(2)若∠A=∠D,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
(3)若AB=DE,BC=EF,
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
(4)若AB=DE,BC=EF,AC=DF
则△ABC与△DEF (填“全等”或“不全等” )
根据 (用简写法)
问题:对于两个直角三角形还有其它的判定方法吗?
二.导入新课
(一)探索练习:(动手操作):
已知线段a ,c (a
1、按步骤作图:
作∠MCN=∠=90°,
在射线 CM上截取线段CB=a,
③以B 为圆心,c为半径画弧,交射线CN于点A,
④连结AB
2、与同桌重叠比较,是否重合?
3、从中你发现了什么?
斜边与一直角边对应相等的两个直角三角形全等.(HL)
小结:你能够用几种方法说明两个直角三角形全等?
直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:SAS、ASA、AAS、SSS,还有直角三角形特殊的判定方法——“HL”.
(二)巩固练习:
1.如图,△ABC中,AB=AC,AD是高,
则△ADB与△ADC (填“全等”或“不全等” )
根据 (用简写法)
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,
(1)若AC//DB,且AC=DB,则△ACE≌△BDF,
根据
(2)若AC//DB,且AE=BF,则△ACE≌△BDF,
根据
(3)若AE=BF,且CE=DF,则△ACE≌△BDF,
根据
(4)若AC=BD,AE=BF,CE=DF。则△ACE≌△BDF,
根据
(5) 若AC=BD,CE=DF(或AE=BF),则△ACE≌△BDF,
根据
3、判断两个直角三角形全等的方法不正确的有( )
两条直角边对应相等 (B)斜边和一锐角对应相等
(C)斜边和一条直角边对应相等 (D)两个锐角对应相等
4、如图,B、E、F、C在同一直线上,AF⊥BC于F,DE⊥BC于E,
AB=DC,BE=CF,你认为AB平行于CD吗?说说你的理由
答:
理由:∵ AF⊥BC,DE⊥BC (已知)
∴ ∠AFB=∠DEC= °(垂直的定义)
在Rt△ 和Rt△ 中
∴ ≌ ( )
∴∠ = ∠ ( )
∴ (内错角相等,两直线平行)
三、例题分析
例1、如图,AC⊥BC,BD⊥AD,AC=BD。求证:BC=AD
例2、如图,DE⊥AB,DF⊥AC,AE=AF,你能找出一对全等三角形吗
如图,两根长度为12米的绳子,一端系在旗杆上,
另一端分别固定在地面两个木桩上,两个木桩离旗
杆底部的距离相等吗?请说明你的理由。
例4、如图,有两个长度相同的滑梯,左边滑梯的高度AC
与右边滑梯水平方向的长度DF相等,两个滑梯的倾
斜角∠ABC和∠DFE的大小有什么关系?
例5、如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E、F,BE=CF。
(1)图中有几对全等的三角形?请一一列出;
(2)选择一对你认为全等的三角形进行证明。
四、课后练习
填空题
1.判定两直角三角形全等的“HL”这种特殊方法指的是____ .
2.直角三角形全等的判定方法有_____ (用简写).
3.如图5-1,E、B、F、C在同一条直线上,若∠D=∠A=90°,EB=FC,AB=DF.则ΔABC≌_____,全等的根据是_____.
图5-1
4.判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和这个角的邻边对应相等;( )
(3)一个锐角和斜边对应相等; ( )
(4)两直角边对应相等; ( )
(5)一条直角边和斜边对应相等. ( )
选择题
5.下列说法正确的是 ( )
A.一直角边对应相等的两个直角三角形全等
B.斜边相等的两个直角三角形全等
C.斜边相等的两个等腰直角三角形全等
D.一边长相等的两等腰直角三角形全等
6.如图5-2,AB=AC,AD⊥ BC于D,E、F为AD上的点,则图中共有( )对全等三角形.
A.3 B.4 C.5 D.6
图5-2
解答题
7.已知:如图5-3,AB⊥BD,CD⊥BD,AD=BC.
求证:(1)AB=DC
(2)AD∥BC.
图5-3
8.已知:如图5-4,AC=BD,AD⊥AC,BC⊥BD.
求证:AD=BC;
图5-4
9.已知:如图5-5,AE⊥AB,BC⊥AB,AE=AB,ED=AC.
求证:ED⊥AC.
图5-5
10.已知:如图5-6,DE⊥AC,BF⊥AC,AD=BC,DE=BF.
求证:AB∥DC.
图5-6
11.用三角板可按下面方法画角平分线:在已知∠AOB的两边上,分别取OM=ON (如图5-7),再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则OP平分∠AOB,请你说出其中的道理.
图5-7
12.(1)已知:如图5-8,线段AC、BD交于O,∠AOB为钝角,AB=CD,BF⊥AC于F,DE⊥AC于E,AE=CF.
求证:BO=DO.
图5-8
(2)若∠AOB为锐角,其他条件不变,请画出图形并判断 (1)中的结论是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
a
c
C
M
N
