人教版九年级数学下27.2.1.3相似三角形判定定理3巩固练习(Word版 含答案)
文档属性
| 名称 | 人教版九年级数学下27.2.1.3相似三角形判定定理3巩固练习(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 349.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 15:24:30 | ||
图片预览


文档简介
27.2.1.3相似三角形判定定理3巩固练习(含答案)
一、选择题
1.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是60°,80°,则这两个三角形
( )
A.一定不相似
B.不一定相似
C.一定相似
D.全等
2.下列各组图形中可能不相似的是( )
A.两个等边三角形
B.各有一个角是45°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
3.在△ABC和△A1B1C1中,∠A=∠A1=90°,添加下列条件不能判定两个三角形相似的是( )
A.∠B=∠B1
B.=
C.=
D.=
4.如图1,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )
图1
A.1对
B.2对
C.3对
D.4对
5.如图2,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则AC的长为( )
图2
A.4
B.4
C.6
D.4
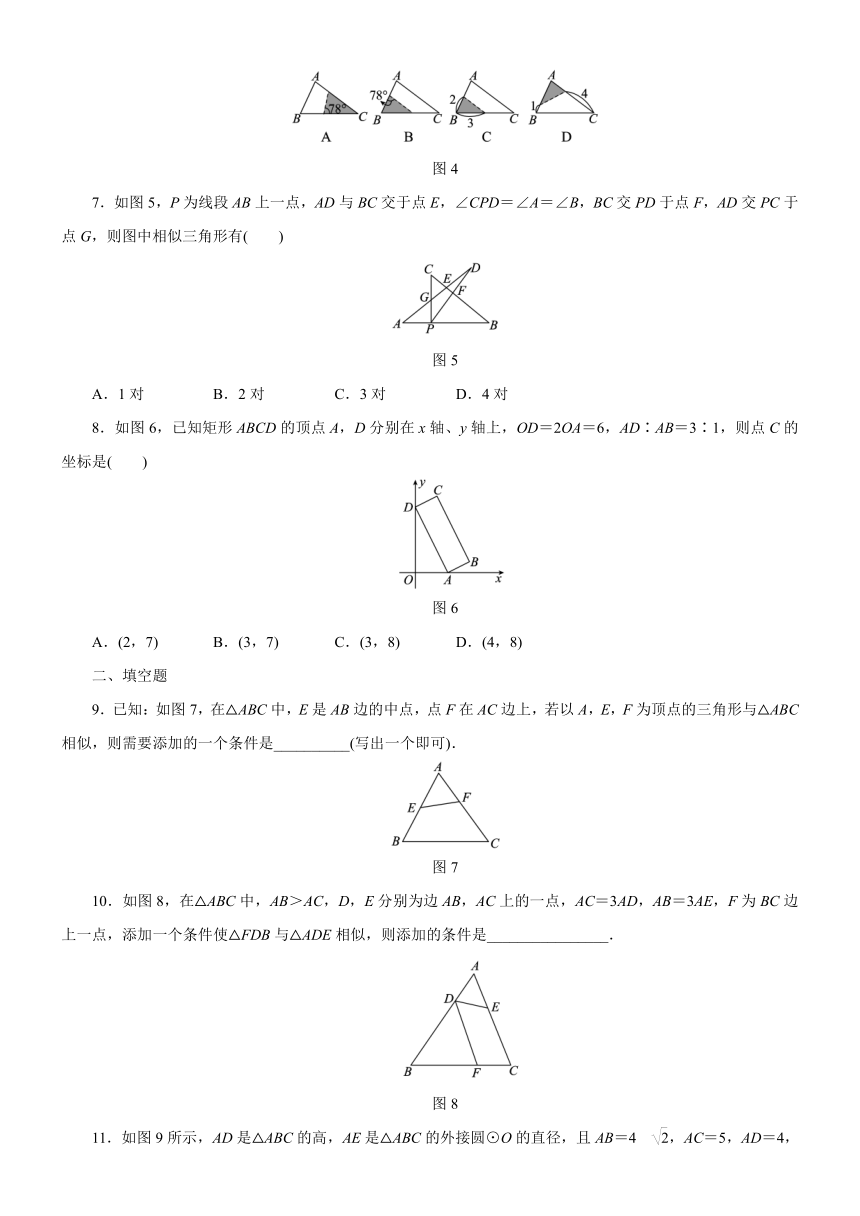
6.如图3,在△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图4中的虚线剪开,则剪下的阴影三角形与原三角形不相似的是
( )
图3
图4
7.如图5,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有( )
图5
A.1对
B.2对
C.3对
D.4对
8.如图6,已知矩形ABCD的顶点A,D分别在x轴、y轴上,OD=2OA=6,AD∶AB=3∶1,则点C的坐标是( )
图6
A.(2,7)
B.(3,7)
C.(3,8)
D.(4,8)
二、填空题
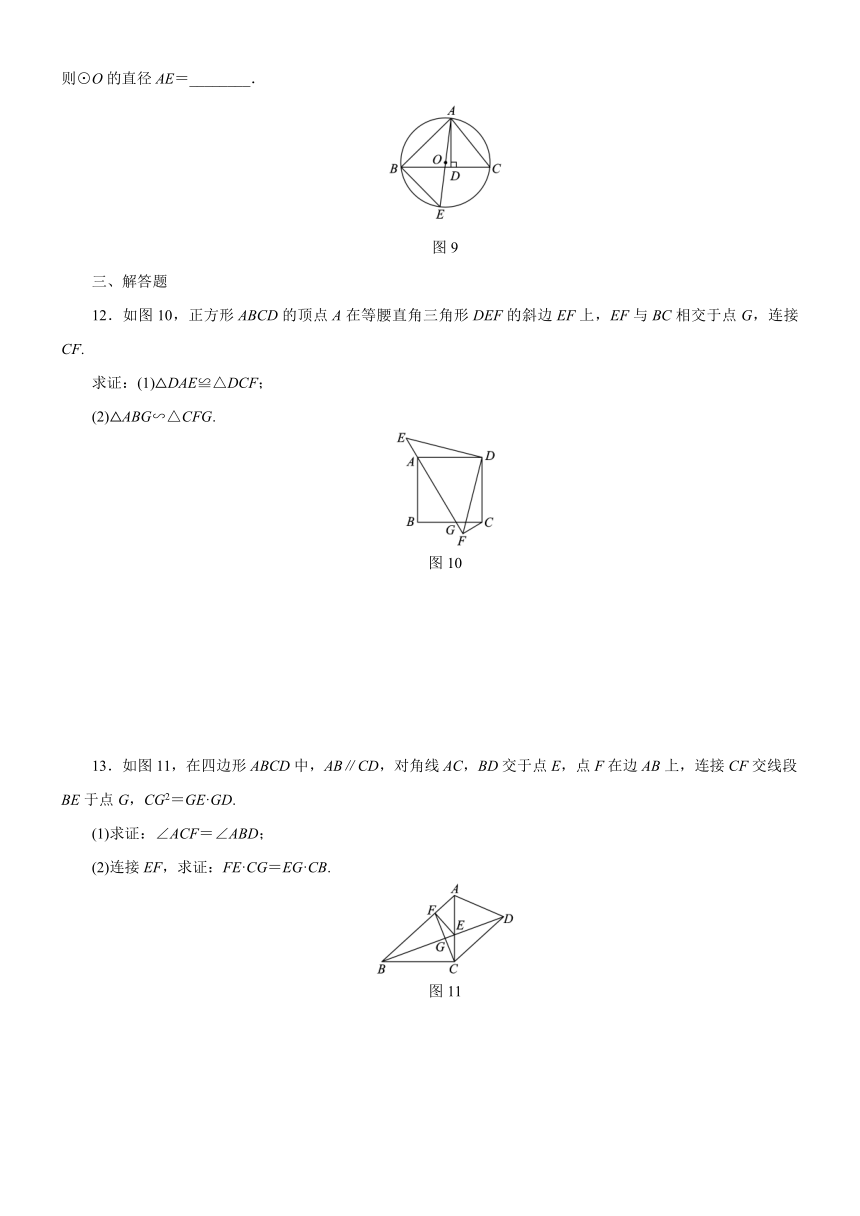
9.已知:如图7,在△ABC中,E是AB边的中点,点F在AC边上,若以A,E,F为顶点的三角形与△ABC相似,则需要添加的一个条件是__________(写出一个即可).
图7
10.如图8,在△ABC中,AB>AC,D,E分别为边AB,AC上的一点,AC=3AD,AB=3AE,F为BC边上一点,添加一个条件使△FDB与△ADE相似,则添加的条件是________________.
图8
11.如图9所示,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4 ,AC=5,AD=4,则⊙O的直径AE=________.
图9
三、解答题
12.如图10,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
求证:(1)△DAE≌△DCF;
(2)△ABG∽△CFG.
图10
13.如图11,在四边形ABCD中,AB∥CD,对角线AC,BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GE·GD.
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:FE·CG=EG·CB.
图11
14.如图12,点D在以AB为直径的⊙O上,AD平分∠BAC,DC⊥AC于点C,过点B作⊙O的切线交AD的延长线于点E.
求证:(1)直线CD是⊙O的切线;
(2)CD·BE=AD·DE.
图12
附加题
逻辑推理如图13,在四边形BFDA中,∠B=90°,DF∥AB,以AD为直径作⊙O,⊙O与BF的一个交点为C,交DF于点E,连接AC,AE,CD,AB=3,BC=4,CF=7.2.
(1)求证:△CDF∽△ACB;
(2)求直径AD的长;
(3)求圆心O到弦ED的距离.
图13
参考答案
1.C [解析]
第一个三角形的第三个内角为180°-40°-60°=80°,所以这两个三角形有两组角对应相等,故它们一定相似.故选C.
2.B [解析]
A选项中,根据三边成比例的两个三角形相似判定这两个三角形相似.B选项中没有指明这个45°的角是顶角还是底角,所以无法判定其相似.C选项中已知一个角为105°,可以判定其为顶角,根据两边成比例且夹角相等的两个三角形相似判定这两个三角形相似.D选项中根据两边成比例且夹角相等的两个三角形相似来判定这两个三角形相似.
3.D
4.C [解析]
由题意可得△ABC∽△ACD,△ACD∽△CBD,△ABC∽△CBD,∴共有3对相似三角形.故选C.
5.B [解析]
∵BC=8,AD是中线,∴DC=4.
在△CBA和△CAD中,∵∠B=∠DAC,∠C=∠C,∴△CBA∽△CAD,∴=,
∴AC2=DC·BC=4×8=32,
∴AC=4
.故选B.
6.C [解析]
A选项,阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意.B选项,阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意.C选项,阴影部分的三角形与原三角形的对应边不成比例,故两三角形不相似,故本选项符合题意.D选项,阴影部分的三角形与原三角形的两边成比例且夹角相等,故两三角形相似,故本选项不符合题意.故选C.
7.C [解析]
△DPG∽△DAP,△CPF∽△CBP,△APG∽△BFP.
8.A [解析]
如图,过点C作CE⊥y轴,垂足为E.
∵OD=2OA=6,∴OA=3.
由题意易得Rt△CED∽Rt△DOA,
∴==.
又∵CD=AB,∴==,
∴CE=2,DE=1,∴OE=7,
∴点C的坐标为(2,7).
9.答案不唯一,如AF=AC或∠AFE=∠B等
10.答案不唯一,如DF∥AC [解析]
∵∠A=∠A,==,
∴△ADE∽△ACB.
当DF∥AC时,△BDF∽△BAC,
∴△BDF∽△EAD.
11.5 [解析]
由圆周角定理可知∠E=∠C.
∵∠ABE=∠ADC=90°,∠E=∠C,
∴△ABE∽△ADC,∴AB?AD=AE?AC.
∵AB=4 ,AC=5,AD=4,
∴4 ?4=AE?5,∴AE=5 .
12.证明:(1)∵△DEF是等腰直角三角形,四边形ABCD是正方形,
∴DE=DF,DA=DC,∠EDF=∠ADC=90°,
∴∠CDF+∠ADF=∠ADE+∠ADF=90°,
∴∠CDF=∠ADE.
在△DAE与△DCF中,
∴△DAE≌△DCF.
(2)∵△DAE≌△DCF,
∴∠DFC=∠DEF=45°.
又∵∠EFD=45°,
∴∠CFG=∠DFC+∠EFD=90°,
∴∠CFG=∠B.
又∵∠CGF=∠AGB,
∴△ABG∽△CFG.
13.证明:(1)∵CG2=GE·GD,
∴=.
又∵∠CGD=∠EGC,
∴△GCD∽△GEC,
∴∠GDC=∠GCE,即∠ACF=∠BDC.
∵AB∥CD,
∴∠ABD=∠BDC,
∴∠ACF=∠ABD.
(2)∵∠ABD=∠ACF,∠BGF=∠CGE,
∴△BGF∽△CGE,
∴=,即=.
又∵∠FGE=∠BGC,
∴△FGE∽△BGC,
∴=,
∴FE·CG=EG·CB.
14.证明:(1)连接OD.
∵AD平分∠BAC,
∴∠CAD=∠BAD.
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∴AC∥OD.
∵CD⊥AC,
∴CD⊥OD.
又∵点D在⊙O上,∴直线CD是⊙O的切线.
(2)连接BD.
∵BE是⊙O的切线,AB为⊙O的直径,
∴∠ABE=∠BDE=90°,
∴∠BAE+∠E=90°.
∵CD⊥AC,∴∠C=90°,
∴∠C=∠BDE,∠CAD+∠ADC=90°.
又∵∠CAD=∠BAE,∴∠ADC=∠E,
∴△ACD∽△BDE,
∴=,
∴CD·BE=AD·DE.
附加题
解:(1)证明:∵∠B=90°,DF∥AB,
∴∠ACB+∠CAB=90°,∠F=90°.
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠ACB+∠DCF=90°,∠B=∠ACD,
∴∠CAB=∠DCF,
∴△CDF∽△ACB.
(2)∵△CDF∽△ACB,
∴=,
即=,
∴DF=9.6.
∵AD是⊙O的直径,
∴∠AED=90°,
∴∠AEF=90°,
∴四边形ABFE是矩形,
∴AE=BF=4+7.2=11.2,EF=AB=3,
∴DE=6.6,
∴AD===13.
(3)过点O作OH⊥DE于点H,
∴OH∥AE.
又∵AO=DO=AD,
∴OH为△AED的中位线,
∴OH=AE=5.6,
即圆心O到弦ED的距离为5.6.
一、选择题
1.已知一个三角形的两个内角分别是40°,60°,另一个三角形的两个内角分别是60°,80°,则这两个三角形
( )
A.一定不相似
B.不一定相似
C.一定相似
D.全等
2.下列各组图形中可能不相似的是( )
A.两个等边三角形
B.各有一个角是45°的两个等腰三角形
C.各有一个角是105°的两个等腰三角形
D.两个等腰直角三角形
3.在△ABC和△A1B1C1中,∠A=∠A1=90°,添加下列条件不能判定两个三角形相似的是( )
A.∠B=∠B1
B.=
C.=
D.=
4.如图1,在△ABC中,∠ACB=90°,CD⊥AB于点D,则图中相似三角形共有( )
图1
A.1对
B.2对
C.3对
D.4对
5.如图2,在△ABC中,AD是中线,BC=8,∠B=∠DAC,则AC的长为( )
图2
A.4
B.4
C.6
D.4
6.如图3,在△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图4中的虚线剪开,则剪下的阴影三角形与原三角形不相似的是
( )
图3
图4
7.如图5,P为线段AB上一点,AD与BC交于点E,∠CPD=∠A=∠B,BC交PD于点F,AD交PC于点G,则图中相似三角形有( )
图5
A.1对
B.2对
C.3对
D.4对
8.如图6,已知矩形ABCD的顶点A,D分别在x轴、y轴上,OD=2OA=6,AD∶AB=3∶1,则点C的坐标是( )
图6
A.(2,7)
B.(3,7)
C.(3,8)
D.(4,8)
二、填空题
9.已知:如图7,在△ABC中,E是AB边的中点,点F在AC边上,若以A,E,F为顶点的三角形与△ABC相似,则需要添加的一个条件是__________(写出一个即可).
图7
10.如图8,在△ABC中,AB>AC,D,E分别为边AB,AC上的一点,AC=3AD,AB=3AE,F为BC边上一点,添加一个条件使△FDB与△ADE相似,则添加的条件是________________.
图8
11.如图9所示,AD是△ABC的高,AE是△ABC的外接圆⊙O的直径,且AB=4 ,AC=5,AD=4,则⊙O的直径AE=________.
图9
三、解答题
12.如图10,正方形ABCD的顶点A在等腰直角三角形DEF的斜边EF上,EF与BC相交于点G,连接CF.
求证:(1)△DAE≌△DCF;
(2)△ABG∽△CFG.
图10
13.如图11,在四边形ABCD中,AB∥CD,对角线AC,BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GE·GD.
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:FE·CG=EG·CB.
图11
14.如图12,点D在以AB为直径的⊙O上,AD平分∠BAC,DC⊥AC于点C,过点B作⊙O的切线交AD的延长线于点E.
求证:(1)直线CD是⊙O的切线;
(2)CD·BE=AD·DE.
图12
附加题
逻辑推理如图13,在四边形BFDA中,∠B=90°,DF∥AB,以AD为直径作⊙O,⊙O与BF的一个交点为C,交DF于点E,连接AC,AE,CD,AB=3,BC=4,CF=7.2.
(1)求证:△CDF∽△ACB;
(2)求直径AD的长;
(3)求圆心O到弦ED的距离.
图13
参考答案
1.C [解析]
第一个三角形的第三个内角为180°-40°-60°=80°,所以这两个三角形有两组角对应相等,故它们一定相似.故选C.
2.B [解析]
A选项中,根据三边成比例的两个三角形相似判定这两个三角形相似.B选项中没有指明这个45°的角是顶角还是底角,所以无法判定其相似.C选项中已知一个角为105°,可以判定其为顶角,根据两边成比例且夹角相等的两个三角形相似判定这两个三角形相似.D选项中根据两边成比例且夹角相等的两个三角形相似来判定这两个三角形相似.
3.D
4.C [解析]
由题意可得△ABC∽△ACD,△ACD∽△CBD,△ABC∽△CBD,∴共有3对相似三角形.故选C.
5.B [解析]
∵BC=8,AD是中线,∴DC=4.
在△CBA和△CAD中,∵∠B=∠DAC,∠C=∠C,∴△CBA∽△CAD,∴=,
∴AC2=DC·BC=4×8=32,
∴AC=4
.故选B.
6.C [解析]
A选项,阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意.B选项,阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意.C选项,阴影部分的三角形与原三角形的对应边不成比例,故两三角形不相似,故本选项符合题意.D选项,阴影部分的三角形与原三角形的两边成比例且夹角相等,故两三角形相似,故本选项不符合题意.故选C.
7.C [解析]
△DPG∽△DAP,△CPF∽△CBP,△APG∽△BFP.
8.A [解析]
如图,过点C作CE⊥y轴,垂足为E.
∵OD=2OA=6,∴OA=3.
由题意易得Rt△CED∽Rt△DOA,
∴==.
又∵CD=AB,∴==,
∴CE=2,DE=1,∴OE=7,
∴点C的坐标为(2,7).
9.答案不唯一,如AF=AC或∠AFE=∠B等
10.答案不唯一,如DF∥AC [解析]
∵∠A=∠A,==,
∴△ADE∽△ACB.
当DF∥AC时,△BDF∽△BAC,
∴△BDF∽△EAD.
11.5 [解析]
由圆周角定理可知∠E=∠C.
∵∠ABE=∠ADC=90°,∠E=∠C,
∴△ABE∽△ADC,∴AB?AD=AE?AC.
∵AB=4 ,AC=5,AD=4,
∴4 ?4=AE?5,∴AE=5 .
12.证明:(1)∵△DEF是等腰直角三角形,四边形ABCD是正方形,
∴DE=DF,DA=DC,∠EDF=∠ADC=90°,
∴∠CDF+∠ADF=∠ADE+∠ADF=90°,
∴∠CDF=∠ADE.
在△DAE与△DCF中,
∴△DAE≌△DCF.
(2)∵△DAE≌△DCF,
∴∠DFC=∠DEF=45°.
又∵∠EFD=45°,
∴∠CFG=∠DFC+∠EFD=90°,
∴∠CFG=∠B.
又∵∠CGF=∠AGB,
∴△ABG∽△CFG.
13.证明:(1)∵CG2=GE·GD,
∴=.
又∵∠CGD=∠EGC,
∴△GCD∽△GEC,
∴∠GDC=∠GCE,即∠ACF=∠BDC.
∵AB∥CD,
∴∠ABD=∠BDC,
∴∠ACF=∠ABD.
(2)∵∠ABD=∠ACF,∠BGF=∠CGE,
∴△BGF∽△CGE,
∴=,即=.
又∵∠FGE=∠BGC,
∴△FGE∽△BGC,
∴=,
∴FE·CG=EG·CB.
14.证明:(1)连接OD.
∵AD平分∠BAC,
∴∠CAD=∠BAD.
∵OA=OD,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∴AC∥OD.
∵CD⊥AC,
∴CD⊥OD.
又∵点D在⊙O上,∴直线CD是⊙O的切线.
(2)连接BD.
∵BE是⊙O的切线,AB为⊙O的直径,
∴∠ABE=∠BDE=90°,
∴∠BAE+∠E=90°.
∵CD⊥AC,∴∠C=90°,
∴∠C=∠BDE,∠CAD+∠ADC=90°.
又∵∠CAD=∠BAE,∴∠ADC=∠E,
∴△ACD∽△BDE,
∴=,
∴CD·BE=AD·DE.
附加题
解:(1)证明:∵∠B=90°,DF∥AB,
∴∠ACB+∠CAB=90°,∠F=90°.
∵AD是⊙O的直径,
∴∠ACD=90°,
∴∠ACB+∠DCF=90°,∠B=∠ACD,
∴∠CAB=∠DCF,
∴△CDF∽△ACB.
(2)∵△CDF∽△ACB,
∴=,
即=,
∴DF=9.6.
∵AD是⊙O的直径,
∴∠AED=90°,
∴∠AEF=90°,
∴四边形ABFE是矩形,
∴AE=BF=4+7.2=11.2,EF=AB=3,
∴DE=6.6,
∴AD===13.
(3)过点O作OH⊥DE于点H,
∴OH∥AE.
又∵AO=DO=AD,
∴OH为△AED的中位线,
∴OH=AE=5.6,
即圆心O到弦ED的距离为5.6.
