长沙市长郡、雅礼、一中 2021届高三年上学期11月份联合编审名校卷 数学(Word含答案解析)
文档属性
| 名称 | 长沙市长郡、雅礼、一中 2021届高三年上学期11月份联合编审名校卷 数学(Word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 699.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-06 19:43:56 | ||
图片预览




文档简介
长郡、雅礼、一中、附中联合编审名校卷
2021届高三月考试卷二(全国卷)
数学(文科)
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求.)
1.已知集合A={x||x|≤2,x∈Z},B={x|x2-x-6<0},则A∩B=
A.{-2,-1,0,1,2,3} B.{-2,-1,0,1,2}
C.{-1,0,1,2} D.{-2,-1,0,1}
2.若z(1+i)=1-i,则z=
A.1-i B.1+i C.-i D.i
3.在等比数列{an}中,已知anan+1=9n,则该数列的公比是
A.-3 B.3 C.±3 D.9
4.已知数据x1,x2,…,x10,2的平均值为2,方差为1,则数据x1,x2,…,x10相对于原数据
A.一样稳定 B.变得比较稳定 C.变得比较不稳定 D.稳定性不可以判断
5.中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹.古代用算筹(一根根同样长短和粗细的小棍子)来进行运算.算筹的摆放有纵式、横式两种(如图所示).当表示一个多位数时,个位、百位、万位数用纵式表示,十位、千位、十万位数用横式表示,以此类推,遇零则置空.例如3266用算筹表示就是,则8771用算筹应表示为
A. B. C. D.
6.过抛物线E:y2=2x焦点的直线交E于A,B两点,线段AB中点M到y轴距离为1,则|AB|=
A.2 B. C.3 D.4
7.如图,在矩形ABCD中,,BC=2,点E为BC的中点,点F在边CD上,若,则的值是
A. B.1 C.2 D.
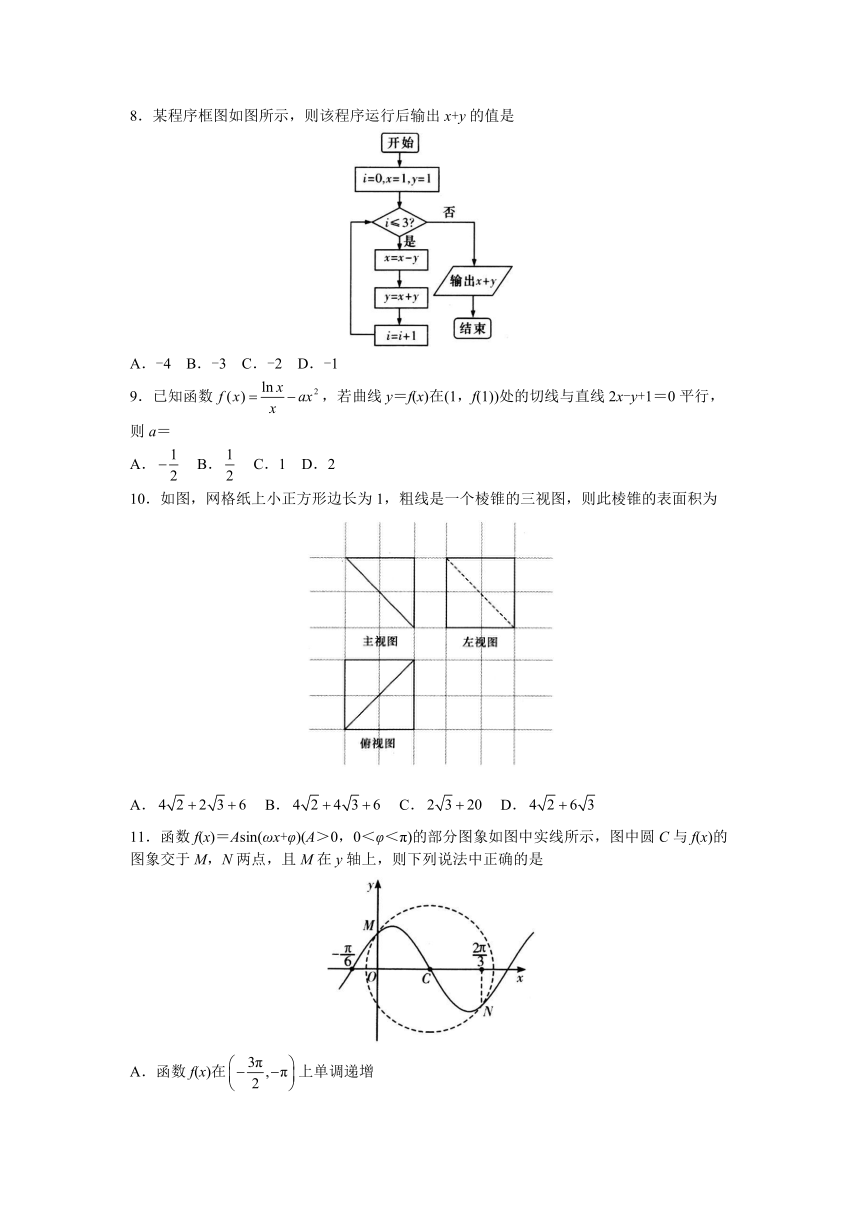
8.某程序框图如图所示,则该程序运行后输出x+y的值是
A.-4 B.-3 C.-2 D.-1
9.已知函数,若曲线y=f(x)在(1,f(1))处的切线与直线2x-y+1=0平行,则a=
A. B. C.1 D.2
10.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的表面积为
A. B. C. D.
11.函数f(x)=Asin(ωx+φ)(A>0,0<φ<π)的部分图象如图中实线所示,图中圆C与f(x)的图象交于M,N两点,且M在y轴上,则下列说法中正确的是
A.函数f(x)在上单调递增
B.函数f(x)的图象关于点成中心对称
C.函数f(x)的图象向右平移个单位后关于直线成轴对称
D.若圆半径为,则函数f(x)的解析式为
12.若0<a<b<c,且abc=1,则下列结论正确的是
①2a+2b>4 ②lg a+lg b<0 ③a+c2>2 ④a2+c>2
A.①② B.②③ C.②④ D.①③
二、填空题
13.若x,y满足约束条件则z=x-2y的最大值为________.
14.设等差数列{an}的前n项和为Sn,S5=23,Sn=360,Sn-5=183,则n=________.
15.过双曲线的下焦点F1作y轴的垂线,交双曲线于A,B两点,若以AB为直径的圆恰好过其上焦点F2,则双曲线的离心率为________.
16.四棱锥P-ABCD的底面ABCD是矩形,侧面PAD⊥平面ABCD,∠APD=120°,AB=PA=PD=2,则该四棱锥P-ABCD外接球的体积为________.
三、解答题(解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.)
(一)必考题
17.已知△ABC的内角A,B,C的对边分别为a,b,c,且,.
(1)求∠C;
(2)求△ABC周长的最大值.
18.如图,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)设点M为线段AB的中点,点N为线段CE的中点.求证:MN∥平面DAE.
19.一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表(单位:辆):
轿车A 轿车B 轿车C
舒适型 100 150 z
标准型 300 450 600
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分x的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数xi(1≤i≤8,i∈N),设样本平均数为,求的概率.
20.设函数f(x)=aex+cos x,其中a∈R.
(1)若a=1,证明:当x>0时,f(x)>2;
(2)若f(x)在区间[0,π]内有两个不同的零点,求a的取值范围.
21.已知点P是圆Q:(x+2)2+y2=32上任意一点,定点R(2,0),线段PR的垂直平分线l与半径PQ相交于M点,当P在圆周上运动时,设点M的运动轨迹为Γ.
(1)求点M的轨迹Γ的方程;
(2)若点N在双曲线(顶点除外)上运动,过点N,R的直线与曲线Γ相交于A,B,过点N,Q的直线与曲线Γ相交于C,D,试探究|AB|+|CD|是否为定值,若为定值请求出这个定值,若不为定值,请说明理由.
(二)选考题:请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,直线l的参数方程为(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2sin θ.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若射线与直线l和曲线C分别交于A,B两点,求|AB|的值.
23.选修4-5:不等式选讲:
已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)若a>0且|x-a|-f(x)≤4恒成立,求实数a的取值范围.
周练(六)
数学(文科)参考答案
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求.)
1.C
2.C 【解析】因为,所以选C.
3.B 【解析】由anan+1=9n>0,∴,∴q2=9,故q=3或q=-3, 当q=-3时,anan+1<0不符合题意.故选B.
4.C 【解析】由题可得:平均值为2, 由,,所以变得不稳定.故选C.
5.C 【解析】由算筹的定义,得,所以8771用算筹应表示为,故选C.
6.C 【解析】设焦点为F,过A,B,M分别作准线的垂线,垂足为A′,B′,M′,则有AA′=AF,BB′=BF,AA′+BB′=2MM′,∵M到y轴距离为1,∴,∴AB=AF+BF=2MM′=3.故选C.
7.D 【解析】据题意,分别以AB、AD所在直线为x,y轴,建立如图所示平面直角坐标系,则:A(0,0),,,设F(x,2);
∴,∴x=1;∴F(1,2),, ;∴.故选D.
8.D
9.A 【解析】函数的导数为,可得曲线y=f(x)在(1,f(1))处的切线的斜率为k=1-2a,由切线与直线2x-y+1=0平行,可得1-2a=2,解得.
10.A 【解析】由已知中的三视图可得:此棱锥的直观图如右图所示:
其底面ABCD为一个底边长是和2的矩形,侧面PBC是边长为的正三角形,侧面ABP,ADP,CDP均是边长为2的等腰直角三角形,其表面积为
,故选A.
11.D 【解析】由图易得点C的横坐标为,所以f(x)的周期T=π,所以ω=2,又,所以,因此.函数f(x)的图象不关于点成中心对称.若圆半径为,则,∴,函数f(x)的解析式为
,故选D.
12.B 【解析】由题意0<a<b<c且abc=1,∴0<a<1,c>1,0<ab<1,bc>1. 2a+2b-4=2a+2b-2abc-2abc=2a(1-2bc)+2b(1-2ac),∵0<a<b<c,∴bc>0,ac>0,2bc>1,2ac>1,所以2a+2b-4<0,所以①错. lg a+lg b=lg ab<0,②正确. ,所以a+c2>2,③正确. 由题意,令b=1,则,,令,(0<a<1),则, 令f′(a)=0,得,所以f(a)在(0,a0)上单调递减,在(a0,1)上单调递增, 所以f(a0)<f(1)=2,所以④错误.故选B.
二、填空题
13.-3 【解析】由x,y满足约束条件作出可行域如图,
化目标函数z=x-2y为, 由图可知,当直线过点A(-1,1)时,直线在y轴上的截距最小,z有最大值为-3.
14.18 【解析】由题意知S5=a1+a2+a3+a4+a5=23, Sn-Sn-5=an+an-1+an-2+an-3+an-4=360-183=177, 两式相加可得:(a1+an)+(a2+an-1)+(a3+an-2)+(a4+an-3)+(a5+an-4)=23+177=200, 所以a1+an=40,,因此n=18.
15. 【解析】过双曲线的下焦点F1作y轴的垂线,交双曲线于A,B两点,则,以AB为直径的圆恰好过其上焦点F2,可得:,∴c2-a2-2ac=0,可得e2-2e-1=0,解得,(舍去).故答案为:.
16. 【解析】取AD的中点E,连接PE,△PAD中,∠APD=120°,PA=PD=2,∴PE=1,,设ABCD的中心为O′,球心为O,则,设O到平面ABCD的距离为d,则R2=d2+22=12+(1+d)2,∴d=1,,∴四棱锥P-ABCD的外接球的体积为.
三、解答题(解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.)
17.【解析】(1)∵, 由正弦定理得:,∵sin A≠0,∴,即, 又0<C<π,∴,故,即;
(2)由(1)可知,, 在△ABC中,由余弦定理得a2+b2-2abcos C=3, 即a2+b2-ab=3,∴,∴,当且仅当a=b时取等号,∴
,即△ABC周长的最大值为.
18.【解析】(1)因为BC⊥平面ABE,AE?平面ABE,所以AE⊥BC, 又BF⊥平面ACE,AE?平面ACE,所以AE⊥BF, 又BF∩BC=B,所以AE⊥平面BCE, 又BE?平面BCE,所以AE⊥BE.
(2)取DE的中点P,连结PA,PN,因为点N为线段CE的中点.
所以PN∥DC,且, 又四边形ABCD是矩形,点M为线段AB的中点,所以AM∥DC,且, 所以PN∥AM,且PN=AM, 故四边形AMNP是平行四边形,所以MN∥AP, 而AP?平面DAE,MN?平面DAE,所以MN∥平面DAE.
19.【解析】(1)设该厂这个月共生产轿车n辆,由题意得,所以n=2000.
则z=2000-(100+300)-(150+450)-600=400.
(2)设所抽样本中有a辆舒适型轿车,由题意,得a=2. 因此抽取的容量为5的样本中,有2辆舒适型轿车,3辆标准型轿车. 用A1,A2表示2辆舒适型轿车,用B1,B2,B3表示3辆标准型轿车,用E表示事件“在该样本中任取2辆,其中至少有1辆舒适型轿车”,则基本事件空间包含的基本事件有: (A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),(B1,B2),(B1,B3),(B2,B3),共10个. 事件E包含的基本事件有:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),共7个. 故,即所求概率为.
(3)样本平均数. 设D表示事件“从样本中任取一数,该数与样本平均数之差的绝对值不超过0.5”,则基本事件空间中有8个基本事件,事件D包括的基本事件有:9.4,8.6,9.2,8.7,9.3,9.0共6个, 所以,即所求概率为.
20.【解析】(1)f′(x)=ex-sin x, 由x>0,得ex>1,sin x∈[-1,1], 则f′(x)=ex-sin x>0,即f(x)在(0,+∞)上为增函数. 故f(x)>f(0)=2,即f(x)>2.
(2)由f(x)=aex+cos x=0,得. 设函数,x∈[0,π], 则
. 令h′(x)=0,得. 则时,h′(x)>0,时,h′(x)<0, 所以h(x)在上单调递增,在上单调递减. 又因为h(0)=-1,h(π)=e-π,, 所以当时,方程在区间[0,π]内有两个不同解, 即所求实数a的取值范围为.
21.【解析】(1)依题意:|MP|=|MR|, 且, 由椭圆定义知点M的轨迹为以R,Q为焦点,长轴长为,焦距为4的椭圆, 即:,c=2,b=2, 故Γ:.
(2)设N(x0,y0),则,x0≠±2,∴直线NR,NQ的斜率都存在,分别设为k1,k2, 则, 将直线NR的方程y=k1(x-2)代入
得, 设A(x1,y1),B(x2,y2),则,
,∴, 同理可得
,∴
.
22.【解析】(1)直线l的参数方程为(t为参数),消去参数可得普通方程:y+x=4(x≠0). 曲线C的极坐标方程为ρ=2sin θ.即ρ2=2ρsin θ,可得普通方程:x2+y2=2y.
(2)射线,即y=x(x>0). 联立解得 联立解得 与直线l和曲线C分别交于A(2,2),B(1,1), .
23.【解析】(1)函数f(x)=|3x+2|,∴不等式f(x)<4-|x-1|化为|3x+2|+|x-1|<4, 当时,不等式化为-3x-2-x+1<4,解得; 当时,3x+2-x+1<4,解得; 当x>1时,3x+2+x-1<4,无解; 综上,不等式的解集为;
(2)令g(x)=|x-a|-f(x), 则 当时,g(x)取得最大值为; 欲使不等式g(x)≤4恒成立,只需,解得; 又因为a>0,所以,即a的取值范围是.
2021届高三月考试卷二(全国卷)
数学(文科)
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求.)
1.已知集合A={x||x|≤2,x∈Z},B={x|x2-x-6<0},则A∩B=
A.{-2,-1,0,1,2,3} B.{-2,-1,0,1,2}
C.{-1,0,1,2} D.{-2,-1,0,1}
2.若z(1+i)=1-i,则z=
A.1-i B.1+i C.-i D.i
3.在等比数列{an}中,已知anan+1=9n,则该数列的公比是
A.-3 B.3 C.±3 D.9
4.已知数据x1,x2,…,x10,2的平均值为2,方差为1,则数据x1,x2,…,x10相对于原数据
A.一样稳定 B.变得比较稳定 C.变得比较不稳定 D.稳定性不可以判断
5.中国有个名句“运筹帷幄之中,决胜千里之外”,其中的“筹”原意是指《孙子算经》中记载的算筹.古代用算筹(一根根同样长短和粗细的小棍子)来进行运算.算筹的摆放有纵式、横式两种(如图所示).当表示一个多位数时,个位、百位、万位数用纵式表示,十位、千位、十万位数用横式表示,以此类推,遇零则置空.例如3266用算筹表示就是,则8771用算筹应表示为
A. B. C. D.
6.过抛物线E:y2=2x焦点的直线交E于A,B两点,线段AB中点M到y轴距离为1,则|AB|=
A.2 B. C.3 D.4
7.如图,在矩形ABCD中,,BC=2,点E为BC的中点,点F在边CD上,若,则的值是
A. B.1 C.2 D.
8.某程序框图如图所示,则该程序运行后输出x+y的值是
A.-4 B.-3 C.-2 D.-1
9.已知函数,若曲线y=f(x)在(1,f(1))处的切线与直线2x-y+1=0平行,则a=
A. B. C.1 D.2
10.如图,网格纸上小正方形边长为1,粗线是一个棱锥的三视图,则此棱锥的表面积为
A. B. C. D.
11.函数f(x)=Asin(ωx+φ)(A>0,0<φ<π)的部分图象如图中实线所示,图中圆C与f(x)的图象交于M,N两点,且M在y轴上,则下列说法中正确的是
A.函数f(x)在上单调递增
B.函数f(x)的图象关于点成中心对称
C.函数f(x)的图象向右平移个单位后关于直线成轴对称
D.若圆半径为,则函数f(x)的解析式为
12.若0<a<b<c,且abc=1,则下列结论正确的是
①2a+2b>4 ②lg a+lg b<0 ③a+c2>2 ④a2+c>2
A.①② B.②③ C.②④ D.①③
二、填空题
13.若x,y满足约束条件则z=x-2y的最大值为________.
14.设等差数列{an}的前n项和为Sn,S5=23,Sn=360,Sn-5=183,则n=________.
15.过双曲线的下焦点F1作y轴的垂线,交双曲线于A,B两点,若以AB为直径的圆恰好过其上焦点F2,则双曲线的离心率为________.
16.四棱锥P-ABCD的底面ABCD是矩形,侧面PAD⊥平面ABCD,∠APD=120°,AB=PA=PD=2,则该四棱锥P-ABCD外接球的体积为________.
三、解答题(解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.)
(一)必考题
17.已知△ABC的内角A,B,C的对边分别为a,b,c,且,.
(1)求∠C;
(2)求△ABC周长的最大值.
18.如图,四边形ABCD为矩形,BC⊥平面ABE,F为CE上的点,且BF⊥平面ACE.
(1)求证:AE⊥BE;
(2)设点M为线段AB的中点,点N为线段CE的中点.求证:MN∥平面DAE.
19.一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如表(单位:辆):
轿车A 轿车B 轿车C
舒适型 100 150 z
标准型 300 450 600
按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分x的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数xi(1≤i≤8,i∈N),设样本平均数为,求的概率.
20.设函数f(x)=aex+cos x,其中a∈R.
(1)若a=1,证明:当x>0时,f(x)>2;
(2)若f(x)在区间[0,π]内有两个不同的零点,求a的取值范围.
21.已知点P是圆Q:(x+2)2+y2=32上任意一点,定点R(2,0),线段PR的垂直平分线l与半径PQ相交于M点,当P在圆周上运动时,设点M的运动轨迹为Γ.
(1)求点M的轨迹Γ的方程;
(2)若点N在双曲线(顶点除外)上运动,过点N,R的直线与曲线Γ相交于A,B,过点N,Q的直线与曲线Γ相交于C,D,试探究|AB|+|CD|是否为定值,若为定值请求出这个定值,若不为定值,请说明理由.
(二)选考题:请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分.
22.选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,直线l的参数方程为(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2sin θ.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若射线与直线l和曲线C分别交于A,B两点,求|AB|的值.
23.选修4-5:不等式选讲:
已知函数f(x)=|3x+2|.
(1)解不等式f(x)<4-|x-1|;
(2)若a>0且|x-a|-f(x)≤4恒成立,求实数a的取值范围.
周练(六)
数学(文科)参考答案
一、选择题(在每小题给出的四个选项中,只有一项是符合题目要求.)
1.C
2.C 【解析】因为,所以选C.
3.B 【解析】由anan+1=9n>0,∴,∴q2=9,故q=3或q=-3, 当q=-3时,anan+1<0不符合题意.故选B.
4.C 【解析】由题可得:平均值为2, 由,,所以变得不稳定.故选C.
5.C 【解析】由算筹的定义,得,所以8771用算筹应表示为,故选C.
6.C 【解析】设焦点为F,过A,B,M分别作准线的垂线,垂足为A′,B′,M′,则有AA′=AF,BB′=BF,AA′+BB′=2MM′,∵M到y轴距离为1,∴,∴AB=AF+BF=2MM′=3.故选C.
7.D 【解析】据题意,分别以AB、AD所在直线为x,y轴,建立如图所示平面直角坐标系,则:A(0,0),,,设F(x,2);
∴,∴x=1;∴F(1,2),, ;∴.故选D.
8.D
9.A 【解析】函数的导数为,可得曲线y=f(x)在(1,f(1))处的切线的斜率为k=1-2a,由切线与直线2x-y+1=0平行,可得1-2a=2,解得.
10.A 【解析】由已知中的三视图可得:此棱锥的直观图如右图所示:
其底面ABCD为一个底边长是和2的矩形,侧面PBC是边长为的正三角形,侧面ABP,ADP,CDP均是边长为2的等腰直角三角形,其表面积为
,故选A.
11.D 【解析】由图易得点C的横坐标为,所以f(x)的周期T=π,所以ω=2,又,所以,因此.函数f(x)的图象不关于点成中心对称.若圆半径为,则,∴,函数f(x)的解析式为
,故选D.
12.B 【解析】由题意0<a<b<c且abc=1,∴0<a<1,c>1,0<ab<1,bc>1. 2a+2b-4=2a+2b-2abc-2abc=2a(1-2bc)+2b(1-2ac),∵0<a<b<c,∴bc>0,ac>0,2bc>1,2ac>1,所以2a+2b-4<0,所以①错. lg a+lg b=lg ab<0,②正确. ,所以a+c2>2,③正确. 由题意,令b=1,则,,令,(0<a<1),则, 令f′(a)=0,得,所以f(a)在(0,a0)上单调递减,在(a0,1)上单调递增, 所以f(a0)<f(1)=2,所以④错误.故选B.
二、填空题
13.-3 【解析】由x,y满足约束条件作出可行域如图,
化目标函数z=x-2y为, 由图可知,当直线过点A(-1,1)时,直线在y轴上的截距最小,z有最大值为-3.
14.18 【解析】由题意知S5=a1+a2+a3+a4+a5=23, Sn-Sn-5=an+an-1+an-2+an-3+an-4=360-183=177, 两式相加可得:(a1+an)+(a2+an-1)+(a3+an-2)+(a4+an-3)+(a5+an-4)=23+177=200, 所以a1+an=40,,因此n=18.
15. 【解析】过双曲线的下焦点F1作y轴的垂线,交双曲线于A,B两点,则,以AB为直径的圆恰好过其上焦点F2,可得:,∴c2-a2-2ac=0,可得e2-2e-1=0,解得,(舍去).故答案为:.
16. 【解析】取AD的中点E,连接PE,△PAD中,∠APD=120°,PA=PD=2,∴PE=1,,设ABCD的中心为O′,球心为O,则,设O到平面ABCD的距离为d,则R2=d2+22=12+(1+d)2,∴d=1,,∴四棱锥P-ABCD的外接球的体积为.
三、解答题(解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.)
17.【解析】(1)∵, 由正弦定理得:,∵sin A≠0,∴,即, 又0<C<π,∴,故,即;
(2)由(1)可知,, 在△ABC中,由余弦定理得a2+b2-2abcos C=3, 即a2+b2-ab=3,∴,∴,当且仅当a=b时取等号,∴
,即△ABC周长的最大值为.
18.【解析】(1)因为BC⊥平面ABE,AE?平面ABE,所以AE⊥BC, 又BF⊥平面ACE,AE?平面ACE,所以AE⊥BF, 又BF∩BC=B,所以AE⊥平面BCE, 又BE?平面BCE,所以AE⊥BE.
(2)取DE的中点P,连结PA,PN,因为点N为线段CE的中点.
所以PN∥DC,且, 又四边形ABCD是矩形,点M为线段AB的中点,所以AM∥DC,且, 所以PN∥AM,且PN=AM, 故四边形AMNP是平行四边形,所以MN∥AP, 而AP?平面DAE,MN?平面DAE,所以MN∥平面DAE.
19.【解析】(1)设该厂这个月共生产轿车n辆,由题意得,所以n=2000.
则z=2000-(100+300)-(150+450)-600=400.
(2)设所抽样本中有a辆舒适型轿车,由题意,得a=2. 因此抽取的容量为5的样本中,有2辆舒适型轿车,3辆标准型轿车. 用A1,A2表示2辆舒适型轿车,用B1,B2,B3表示3辆标准型轿车,用E表示事件“在该样本中任取2辆,其中至少有1辆舒适型轿车”,则基本事件空间包含的基本事件有: (A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),(B1,B2),(B1,B3),(B2,B3),共10个. 事件E包含的基本事件有:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A2,B1),(A2,B2),(A2,B3),共7个. 故,即所求概率为.
(3)样本平均数. 设D表示事件“从样本中任取一数,该数与样本平均数之差的绝对值不超过0.5”,则基本事件空间中有8个基本事件,事件D包括的基本事件有:9.4,8.6,9.2,8.7,9.3,9.0共6个, 所以,即所求概率为.
20.【解析】(1)f′(x)=ex-sin x, 由x>0,得ex>1,sin x∈[-1,1], 则f′(x)=ex-sin x>0,即f(x)在(0,+∞)上为增函数. 故f(x)>f(0)=2,即f(x)>2.
(2)由f(x)=aex+cos x=0,得. 设函数,x∈[0,π], 则
. 令h′(x)=0,得. 则时,h′(x)>0,时,h′(x)<0, 所以h(x)在上单调递增,在上单调递减. 又因为h(0)=-1,h(π)=e-π,, 所以当时,方程在区间[0,π]内有两个不同解, 即所求实数a的取值范围为.
21.【解析】(1)依题意:|MP|=|MR|, 且, 由椭圆定义知点M的轨迹为以R,Q为焦点,长轴长为,焦距为4的椭圆, 即:,c=2,b=2, 故Γ:.
(2)设N(x0,y0),则,x0≠±2,∴直线NR,NQ的斜率都存在,分别设为k1,k2, 则, 将直线NR的方程y=k1(x-2)代入
得, 设A(x1,y1),B(x2,y2),则,
,∴, 同理可得
,∴
.
22.【解析】(1)直线l的参数方程为(t为参数),消去参数可得普通方程:y+x=4(x≠0). 曲线C的极坐标方程为ρ=2sin θ.即ρ2=2ρsin θ,可得普通方程:x2+y2=2y.
(2)射线,即y=x(x>0). 联立解得 联立解得 与直线l和曲线C分别交于A(2,2),B(1,1), .
23.【解析】(1)函数f(x)=|3x+2|,∴不等式f(x)<4-|x-1|化为|3x+2|+|x-1|<4, 当时,不等式化为-3x-2-x+1<4,解得; 当时,3x+2-x+1<4,解得; 当x>1时,3x+2+x-1<4,无解; 综上,不等式的解集为;
(2)令g(x)=|x-a|-f(x), 则 当时,g(x)取得最大值为; 欲使不等式g(x)≤4恒成立,只需,解得; 又因为a>0,所以,即a的取值范围是.
同课章节目录
