4.4.1 对数函数的概念学案
文档属性
| 名称 | 4.4.1 对数函数的概念学案 |  | |
| 格式 | zip | ||
| 文件大小 | 531.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 16:24:56 | ||
图片预览




文档简介
对数函数的概念
一般地,把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自变量,定义域是(0,+∞)
2.对数函数的图像和性质
定义
形如(且)的函数叫做对数函数
定义域
值域
图像
性质
奇偶性
非奇非偶函数
单调性
在上是增函数
上是减函数
范围
当时,;
当时,
当时,;
当时,
定点
题型一
对数函数的概念
注意:判断一个函数是对数函数必须是形如y=logax(a>0且a≠1)的形式,即必须满足以下条件:
(1)系数为1.(2)底数为大于0且不等于1的常数.(3)对数的真数仅有自变量x.
例1
指出下列函数哪些是对数函数?
(1)y=3log2x;(2)y=log6x;(3)y=logx3;(4)y=log2x+1.
[跟踪训练]1(1)对数函数的图象过点M(16,4),则此对数函数的解析式为
(2)若对数函数y=f(x)满足f(4)=2,则该对数函数的解析式为( )
A.y=log2x
B.y=2log4x
C.y=log2x或y=2log4x
D.不确定
题型二 对数型函数的定义域
注意:求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数大于零且不等于1.
例2 求下列函数的定义域.
(1)y=loga(3-x)+loga(3+x);(2)y=log2(16-4x).
[跟踪训练]2
求下列函数的定义域.
(1)y=;(2)y=;
(3)y=;(4)y=log(x+1)(2-x).
题型三 比较对数值的大小
例3
比较下列各组中两个值的大小:
(1)log31.9,log32;
(2)log23,log0.32;
(3)logaπ,loga3.14(a>0,a≠1).
[跟踪训练]1下列不等式成立的是(其中a>0且a≠1)( )
A.loga5.1B.log2.1>log2.2
C.log1.1(a+1)D.log32.9题型四
对数函数的图象
注意:(1)明确图象的分布区域.对数函数的图象在第一、四象限.当x趋近于0时,函数图象会越来越靠近y轴,但永远不会与y轴相交.
(2)建立分类讨论的思想.在画对数函数图象之前要先判断对数的底数a的取值范围是a>1,还是0(3)牢记特殊点.对数函数y=logax(a>0,且a≠1)的图象经过点:(1,0),(a,1)和.
例4 画出函数y=lg|x-1|的图象.
例5
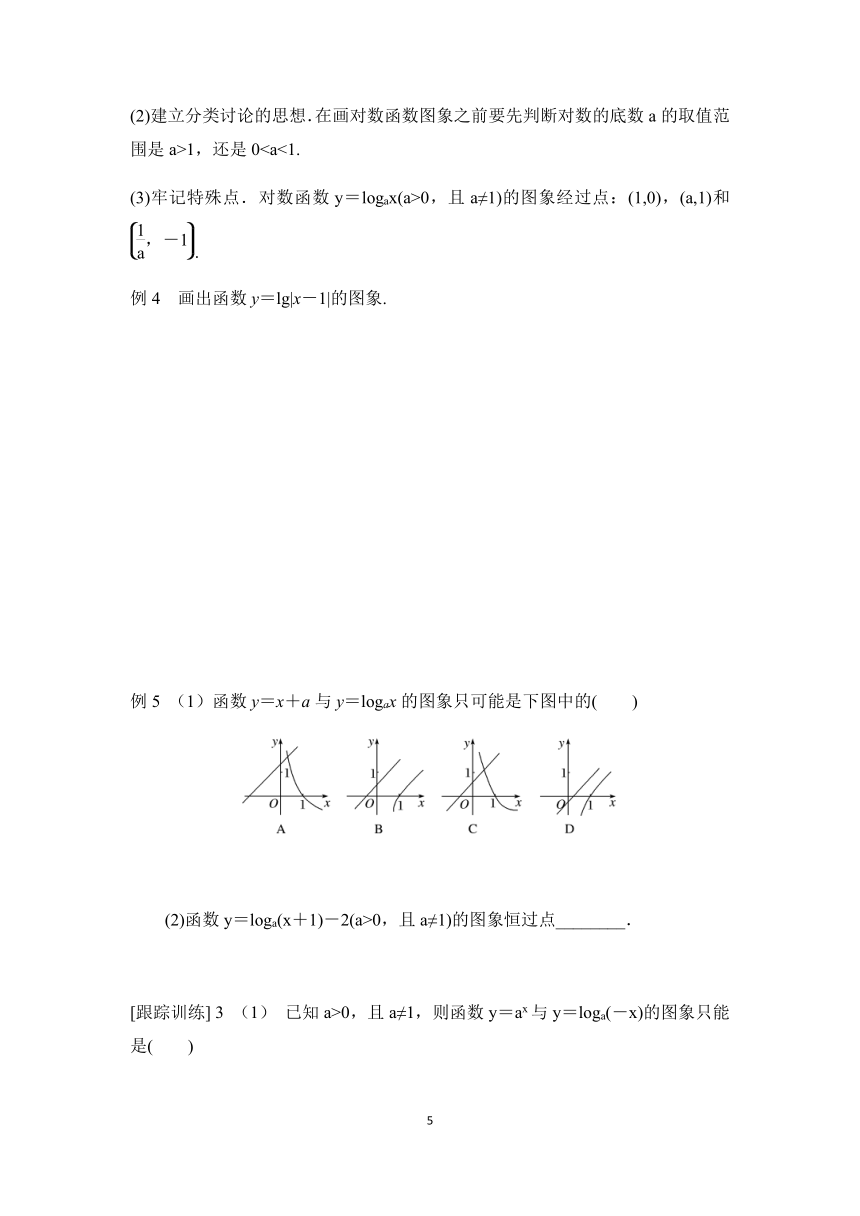
(1)函数y=x+a与y=logax的图象只可能是下图中的( )
(2)函数y=loga(x+1)-2(a>0,且a≠1)的图象恒过点________.
[跟踪训练]
3
(1)
已知a>0,且a≠1,则函数y=ax与y=loga(-x)的图象只能是( )
(2)y=loga+2图象恒过定点坐标是________.
例6.已知函数y=lg(ax2+2ax+1):
(1)若函数的定义域为R,求a的取值范围;
(2)若函数的值域为R,求a的取值范围.
(1)对数函数图像必经过第一、四象限,在第一象限的规律是:
以直线把第一象限分成两个区域,每个区域里对数函数底数都是由左向右逐渐增大,如右图所示,,,,对应,,,,则;
(2)与关于轴对称;
(3)轴是渐进线,即图像向上、下无限延伸;
1.思考辨析
1.下列函数中,是对数函数的是( )
A.y=logxa(x>0且x≠1)
B.y=log2x-1
C.y=2lg8x
D.y=log5x
2.已知对数函数的图象过点M(9,2),则此对数函数的解析式为( )
A.y=log2x
B.y=log3x
C.y=x
D.y=x
3.函数f(x)=+lg(x+1)的定义域为( )
A.[-1,3)
B.(-1,3)
C.(-1,3]
D.[-1,3]
4.已知函数f(x)=log3(x+1),若f(a)=1,则a等于( )
A.0
B.1
C.2
D.3
5.函数y=lg(x+1)的图象大致是( )
6.图中曲线是对数函数的图象,已知取,,,四个值,则相应于,,,的值依次为
A.,,,
B.,,,
C.,,,
D.,,,
7.设则(
)
A.a>b>c
B.a>c>b
C.b>a>c
D.b>c>a
8.满足“对定义域内任意实数x,y,都有f(xy)=f(x)+f(y)”的函数f(x)可以是( )
A.f(x)=x2
B.f(x)=2x
C.f(x)=log2x
D.f(x)=elnx
9.如果函数y=log2x的图象经过点A(4,y0),那么y0=____.
10.函数y=(3x-2)的定义域是____.
11.已知函数y=loga(x-3)-1的图象恒过定点P,则点P的坐标是________.
12.已知函数f(x)=lg(x2+ax+1)的定义域是R,则实数a的取值范围是_______.
13.函数f(x)=的图象如图所示,则a+b+c=___.
14..已知对数函数f(x)=(m2-m-1)log(m+1)x,求f(27).
15.已知f(x)=lg,x∈(-1,1),若f(a)=,求f(-a).
16.求下列各式中x的取值范围:
(1);(2);(3).
17.比较下列各组值的大小:
(1),;(2)log1.51.6,log1.51.4;(3)log0.57,log0.67;(4)log3π,log20.8.
18..已知函数f(x)=(1)求f?的值;(2)若f(a)=,求a的值.
19.若函数的定义域为一切实数,求实数的取值范围.
1.下列函数中,是对数函数的是( )
A.y=logxa(x>0且x≠1)
B.y=log2x-1
C.y=2lg8x
D.y=log5x
2.已知对数函数的图象过点M(9,2),则此对数函数的解析式为(
)
A.y=log2x
B.y=log3x
C.y=x
D.y=x
3.函数f(x)=ln(1-x)的定义域是(
)
A.(0,1)
B.[0,1)
C.(1,+∞)
D.(-∞,1)
4.y=2x与y=log2x的图象关于(
)
A.x轴对称
B.直线y=x对称
C.原点对称
D.y轴对称
5.设a=log32,b=log52,c=log23,则(
D )
A.a>c>b
B.b>c>a
C.c>b>a
D.c>a>b
6.函数y=loga(3x-2)+2(a>0,且a≠1)的图象必过定点(
)
A(1,2)
B
(2,2)
C
(2,3)
D
(,2)
7.
如果函数y=log2x的图象经过点A(4,y0),那么y0=
.
8.设ln
b>ln
a>ln
c,则a,b,c的大小关系为
.
9.若函数f(x)=logax(010.下列给出的函数:①y=log5x+1;
②y=logax2(a>0,且a≠1);③y=lox;
④y=log3x;⑤y=logx(x>0,且x≠1);
⑥y=lox.其中是对数函数的为(
)
A③④⑤
B②④⑥
C①③⑤⑥
D③⑥
11.已知函数f(x)=loga(x+2),若其图象过点(6,3),则f(2)的值为( )
A.-2
B.2
C.
D.-
12.函数y=+lg(2x+1)的定义域( )
A.(,3]
B.(,3)
C.(-,3]
D.(-,3)
13.已知函数f(x)=ln
x,g(x)=lg
x,h(x)=log3x,直线y=a(a<0)与这三个函数的交点的横坐标分别是x1,x2,x3,则x1,x2,x3的大小关系是( )
A.
x2B.
x1C.
x1D.
x314.函数y=log2|x|的图象大致是(
)
15.若loga<1,则a的取值范围为
.
16.若对数函数f(x)=(a2-2a-2)logax,则f(9)=
.
17.求下列函数的定义域:
(1)y=log5(1-x);(2)y=log(3x-1)5;(3)y=.
18.比较下列各组数的大小;
(1)log0.90.8,log0.90.7,log0.80.9;
(2)log32,log23,log4.
题型一
对数函数的概念
注意:判断一个函数是对数函数必须是形如y=logax(a>0且a≠1)的形式,即必须满足以下条件:
(1)系数为1.(2)底数为大于0且不等于1的常数.(3)对数的真数仅有自变量x.
例1
指出下列函数哪些是对数函数?
(1)y=3log2x;(2)y=log6x;
(3)y=logx3;(4)y=log2x+1.
(1)log2x的系数是3,不是1,不是对数函数.
(2)符合对数函数的结构形式,是对数函数.
(3)自变量在底数位置上,不是对数函数.
(4)对数式log2x后又加1,不是对数函数.
[跟踪训练]1(1)对数函数的图象过点M(16,4),则此对数函数的解析式为
(2)若对数函数y=f(x)满足f(4)=2,则该对数函数的解析式为( )
A.y=log2x
B.y=2log4x
C.y=log2x或y=2log4x
D.不确定
(1)
y=log2x
[解析] 设对数函数为y=logax,则4=loga16,∴a4=16,
∴a=2,∴y=log2x.
(2)A
[解析] 设对数函数的解析式为y=logax(a>0,且a≠1),由题意可知loga4=2,
∴a2=4,∴a=2.
∴该对数函数的解析式为y=log2x.
题型二 对数型函数的定义域
注意:求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数大于零且不等于1.
例2 求下列函数的定义域.
(1)y=loga(3-x)+loga(3+x);
(2)y=log2(16-4x).
解 (1)由得-3∴函数的定义域是(-3,3).
(2)由16-4x>0,得4x<16=42,
由指数函数的单调性得x<2,
∴函数y=log2(16-4x)的定义域为(-∞,2).
[跟踪训练]2
求下列函数的定义域.
(1)y=;(2)y=;
(3)y=;(4)y=log(x+1)(2-x).
(1)定义域为(0,+∞).
(2)由解得(3)由解得(4)由解得-1题型三 比较对数值的大小
例3
比较下列各组中两个值的大小:
(1)log31.9,log32;
(2)log23,log0.32;
(3)logaπ,loga3.14(a>0,a≠1).
解 (1)因为y=log3x在(0,+∞)上是增函数,所以log31.9(2)因为log23>log21=0,log0.32log0.32.
(3)当a>1时,函数y=logax在(0,+∞)上是增函数,则有logaπ>loga3.14;
当0综上所得,当a>1时,logaπ>loga3.14;当0[跟踪训练]1下列不等式成立的是(其中a>0且a≠1)( )
A.loga5.1B.log2.1>log2.2
C.log1.1(a+1)D.log32.9对于选项A,因为a和1大小的关系不确定,无法确定指数函数和对数函数的单调性,故A不成立;对于选项B,因为以为底的对数函数是减函数,所以成立;对于选项C,因为以1.1为底的对数函数是增函数,所以不成立;对于选项D,log32.9>0,log0.52.2<0,故不成立,故选B.
题型四
对数函数的图象
注意:(1)明确图象的分布区域.对数函数的图象在第一、四象限.当x趋近于0时,函数图象会越来越靠近y轴,但永远不会与y轴相交.
(2)建立分类讨论的思想.在画对数函数图象之前要先判断对数的底数a的取值范围是a>1,还是0(3)牢记特殊点.对数函数y=logax(a>0,且a≠1)的图象经过点:(1,0),(a,1)和.
例4 画出函数y=lg|x-1|的图象.
解 (1)先画出函数y=lg
x的图象(如图).
(2)再画出函数y=lg|x|的图象(如图).
(3)最后画出函数y=lg|x-1|的图象(如图).
例5
(1)函数y=x+a与y=logax的图象只可能是下图中的( )
(2)函数y=loga(x+1)-2(a>0,且a≠1)的图象恒过点________.
(1) C
(2)(0,-2)
因为函数y=logax
(a>0,且a≠1)的图象恒过点(1,0),则令x+1=1得x=0,此时y=loga(x+1)-2=-2,所以函数y=loga(x+1)-2(a>0,且a≠1)的图象恒过点(0,-2).
[跟踪训练]
3
(1)
已知a>0,且a≠1,则函数y=ax与y=loga(-x)的图象只能是( )
(2)y=loga+2图象恒过定点坐标是________.
(1)
B
若01,则函数y=ax的图象上升且过点(0,1),而函数y=loga(-x)的图象下降且过点(-1,0),只有B中图象符合.
(2)(-2,2)
[解析] 令=1,得x=-2,此时y=2,∴函数y=loga+2过定点(-2,2).
例6.已知函数y=lg(ax2+2ax+1):
(1)若函数的定义域为R,求a的取值范围;
(2)若函数的值域为R,求a的取值范围.
【分析】(1)由于函数的定义域为R,可得ax2+2ax+1>0恒成立.当a=0时,显然成立,当a≠0时,应有a>0且△=4a2﹣4a<0,由此求得a的取值范围.
(2)若函数的值域为R,则ax2+2ax+1能取遍所有的正整数,故有
a>0且△=4a2﹣4a≥0,由此求得a的取值范围.
【解答】解:(1)∵函数的定义域为R,∴ax2+2ax+1>0恒成立.当a=0时,显然成立.
当a≠0时,应有a>0且△=4a2﹣4a<0,解得
a<1.
故a的取值范围为[0,1).
(2)若函数的值域为R,则ax2+2ax+1能取遍所有的正整数,∴a>0且△=4a2﹣4a≥0.
解得
a≥1,故a的取值范围为[1,+∞).
(1)对数函数图像必经过第一、四象限,在第一象限的规律是:
以直线把第一象限分成两个区域,每个区域里对数函数底数都是由左向右逐渐增大,如右图所示,,,,对应,,,,则;
(2)与关于轴对称;
(3)轴是渐进线,即图像向上、下无限延伸;
1.思考辨析
1.下列函数中,是对数函数的是( D )
A.y=logxa(x>0且x≠1)
B.y=log2x-1
C.y=2lg8x
D.y=log5x
[解析] A、B、C都不符合对数函数的定义,故选D.
2.已知对数函数的图象过点M(9,2),则此对数函数的解析式为( B )
A.y=log2x
B.y=log3x
C.y=x
D.y=x
[解析] 设对数函数为y=logax,则2=loga9,
∴a2=9,∴a=3,∴y=log3x,故选B.
3.函数f(x)=+lg(x+1)的定义域为( )C
A.[-1,3)
B.(-1,3)
C.(-1,3]
D.[-1,3]
4.已知函数f(x)=log3(x+1),若f(a)=1,则a等于( )C
A.0
B.1
C.2
D.3
5.函数y=lg(x+1)的图象大致是( )C
6.图中曲线是对数函数的图象,已知取,,,四个值,则相应于,,,的值依次为
A.,,,
B.,,,
C.,,,
D.,,,
【答案】A
【解析】
由已知中曲线是对数函数的图象,
由对数函数的图象和性质,可得,,,的值从小到大依次为:,,,,
由取,,,四个值,
故,,,的值依次为,,,,
故选:.
7.设则(
)
A.a>b>c
B.a>c>b
C.b>a>c
D.b>c>a
【答案】A
【解析】
,
.
故选:A.
8.满足“对定义域内任意实数x,y,都有f(xy)=f(x)+f(y)”的函数f(x)可以是( C )
A.f(x)=x2
B.f(x)=2x
C.f(x)=log2x
D.f(x)=elnx
[解析] ∵对数运算律中有logaM+logaN=loga(MN),
∴f(x)=log2x满足题目要求.
9.如果函数y=log2x的图象经过点A(4,y0),那么y0=__2__.
[解析] 将A(4,y0)代入y=log2x得log24=y0,∴y0=2.
10.函数y=(3x-2)的定义域是__(,+∞)__.
[解析] 由3x-2>0得x>,所以函数的定义域为(,+∞).
11.已知函数y=loga(x-3)-1的图象恒过定点P,则点P的坐标是________.
(4,-1)
[解析] y=logax的图象恒过点(1,0),令x-3=1,得x=4,则y=-1.
12.已知函数f(x)=lg(x2+ax+1)的定义域是R,则实数a的取值范围是__(-2,2)__.
[解析] 由题意知x2+ax+1>0恒成立,所以Δ=a2-4<0,即-213.函数f(x)=的图象如图所示,则a+b+c=____.
[解析] 由题图可求得直线的方程为y=2x+2,即a=2,b=2,又函数y=logc的图象过点(0,2),将其坐标代入可得c=,所以a+b+c=2+2+=.
14..已知对数函数f(x)=(m2-m-1)log(m+1)x,求f(27).
[解析] ∵f(x)是对数函数,∴,
解得m=2.
∴f(x)=log3x,∴f(27)=log327=3.
15.已知f(x)=lg,x∈(-1,1),若f(a)=,求f(-a).
[解析] 解法一:∵f(-x)=lg=lg()-1=-f(x),∴f(-a)=-f(a)=-.
解法二:f(a)=lg,
f(-a)=lg=lg()-1=-lg=-.
16.求下列各式中x的取值范围:
(1);
(2);
(3).
(1),,解得:或,
的取值范围是.
(2)
,解得:,
的取值范围是.
(3)
,解得:,
的取值范围是.
17.比较下列各组值的大小:
(1),;
(2)log1.51.6,log1.51.4;
(3)log0.57,log0.67;
(4)log3π,log20.8.
18..已知函数f(x)=(1)求f?的值;(2)若f(a)=,求a的值.
解 (1)∵f?=log3=-3,∴f?=f(-3)=2-3=.
(2)当a>0时,由f(a)=,得log3a=.∴a==.
当a≤0时,由f(a)=,得2a=,∴a=-1,
综上所述a的值为-1或.
19.若函数的定义域为一切实数,求实数的取值范围.
解析:因为函数的定义域为一切,
等价于,对任意的实数恒成立.
当时,,符合条件.
当时,.
综上.
故答案为:
1.下列函数中,是对数函数的是( )
A.y=logxa(x>0且x≠1)
B.y=log2x-1
C.y=2lg8x
D.y=log5x
2.已知对数函数的图象过点M(9,2),则此对数函数的解析式为(
)
A.y=log2x
B.y=log3x
C.y=x
D.y=x
3.函数f(x)=ln(1-x)的定义域是(
)
A.(0,1)
B.[0,1)
C.(1,+∞)
D.(-∞,1)
4.y=2x与y=log2x的图象关于(
)
A.x轴对称
B.直线y=x对称
C.原点对称
D.y轴对称
5.设a=log32,b=log52,c=log23,则(
D )
A.a>c>b
B.b>c>a
C.c>b>a
D.c>a>b
6.函数y=loga(3x-2)+2(a>0,且a≠1)的图象必过定点(
)
A(1,2)
B
(2,2)
C
(2,3)
D
(,2)
7.
如果函数y=log2x的图象经过点A(4,y0),那么y0=
.
8.设ln
b>ln
a>ln
c,则a,b,c的大小关系为
.
9.若函数f(x)=logax(010.下列给出的函数:①y=log5x+1;
②y=logax2(a>0,且a≠1);③y=lox;
④y=log3x;⑤y=logx(x>0,且x≠1);
⑥y=lox.其中是对数函数的为(
)
A③④⑤
B②④⑥
C①③⑤⑥
D③⑥
11.已知函数f(x)=loga(x+2),若其图象过点(6,3),则f(2)的值为( )
A.-2
B.2
C.
D.-
12.函数y=+lg(2x+1)的定义域( )
A.(,3]
B.(,3)
C.(-,3]
D.(-,3)
13.已知函数f(x)=ln
x,g(x)=lg
x,h(x)=log3x,直线y=a(a<0)与这三个函数的交点的横坐标分别是x1,x2,x3,则x1,x2,x3的大小关系是( )
A.
x2B.
x1C.
x1D.
x314.函数y=log2|x|的图象大致是(
)
15.若loga<1,则a的取值范围为
.
16.若对数函数f(x)=(a2-2a-2)logax,则f(9)=
.
17.求下列函数的定义域:
(1)y=log5(1-x);
(2)y=log(3x-1)5;
(3)y=.
18.比较下列各组数的大小;
(1)log0.90.8,log0.90.7,log0.80.9;
(2)log32,log23,log4.
【参考答案】
1.
D
[解析]
A、B、C都不符合对数函数的定义,故选D.
2.
B
[解析]设对数函数为y=logax,则2=loga9,∴a2=9,∴a=3,∴y=log3x,故选B.
3.
D
[解析]由1-x>0得x<1,故选D.
4.
B
解析]函数y=2x与函数y=log2x是互为反函数,故它们的图象关于直线y=x对称.
5.
D
解析]
a=log32log22=1,由对数函数的性质知log526.
A
解析:令3x-2=1,得x=1,又loga(3×1-2)+2=2,故定点为(1,2),选A.
7.
2
[解析] 将A(4,y0)代入y=log2x得log24=y0,∴y0=2.
8.
b>a>c
解析:由对数函数的图象与性质可知,函数y=ln
x在(0,+∞)上为单调递增函数,因为ln
b>ln
a>ln
c,所以b>a>c.
9.[解析] 由题意得f(x)max=logaa=1,f(x)min=loga(2a)=1+loga2,∴1=3×(1+loga2),∴a=.
10.
D
解析:①②④不满足对数函数解析式特征,⑤中真数是常数,故只有③⑥是对数函数.选D.
11.
B
[解析] 由题意得3=loga8,∴a3=8,∴a=2.∴f(x)=log2(x+2),∴f(2)=log24=2.
12.
D
[解析] 由题意得,∴-13.A
解析:令a=-1,得ln
x1=-1,lg
x2=-1,log3x3=-1,故x1=,x2=,x3=,则x1>x3>x2.选A.
14.
A
解析:函数y=log2|x|为偶函数,且x>0时,y=log2x,故选A.
15.
0<a<或a>1
解析 loga<1即loga<logaa,当a>1时,函数y=logax在定义域内是增函数,所以loga<logaa总成立;
当0<a<1时,函数y=logax在定义域内是减函数,由loga<logaa,得a<,故0<a<.
故a的取值范围为0<a<或a>1.
解析:由对数函数定义知故a=3或a=-1(舍去),则f(x)=log3x,故f(9)=log39=2.
17 (1)要使函数式有意义,需1-x>0,解得x<1,
所以函数y=log5(1-x)的定义域是{x|x<1}.
(2)要使函数式有意义,需
解得x>,且x≠,
所以函数y=log(3x-1)5的定义域是.
(3)要使函数式有意义,需
解得x<4,且x≠3,
所以函数y=的定义域是{x|x<4,且x≠3}.
18.(1)log0.80.9<log0.90.8<log0.90.7;(2)log4<log32<log23
【解析】(1)因为y=log0.9x在(0,+∞)上是减函数,且0.9>0.8>0.7,所以1<log0.90.8<log0.90.7.
又因为log0.80.9<log0.80.8=1,所以log0.80.9<log0.90.8<log0.90.7.
(2)由log31<log32<log33,得0<log32<1.
又因为log23>log22=1,log4<log41=0,所以log4<log32<log23.
一般地,把函数y=logax(a>0,且a≠1)叫做对数函数,其中x是自变量,定义域是(0,+∞)
2.对数函数的图像和性质
定义
形如(且)的函数叫做对数函数
定义域
值域
图像
性质
奇偶性
非奇非偶函数
单调性
在上是增函数
上是减函数
范围
当时,;
当时,
当时,;
当时,
定点
题型一
对数函数的概念
注意:判断一个函数是对数函数必须是形如y=logax(a>0且a≠1)的形式,即必须满足以下条件:
(1)系数为1.(2)底数为大于0且不等于1的常数.(3)对数的真数仅有自变量x.
例1
指出下列函数哪些是对数函数?
(1)y=3log2x;(2)y=log6x;(3)y=logx3;(4)y=log2x+1.
[跟踪训练]1(1)对数函数的图象过点M(16,4),则此对数函数的解析式为
(2)若对数函数y=f(x)满足f(4)=2,则该对数函数的解析式为( )
A.y=log2x
B.y=2log4x
C.y=log2x或y=2log4x
D.不确定
题型二 对数型函数的定义域
注意:求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数大于零且不等于1.
例2 求下列函数的定义域.
(1)y=loga(3-x)+loga(3+x);(2)y=log2(16-4x).
[跟踪训练]2
求下列函数的定义域.
(1)y=;(2)y=;
(3)y=;(4)y=log(x+1)(2-x).
题型三 比较对数值的大小
例3
比较下列各组中两个值的大小:
(1)log31.9,log32;
(2)log23,log0.32;
(3)logaπ,loga3.14(a>0,a≠1).
[跟踪训练]1下列不等式成立的是(其中a>0且a≠1)( )
A.loga5.1
C.log1.1(a+1)
对数函数的图象
注意:(1)明确图象的分布区域.对数函数的图象在第一、四象限.当x趋近于0时,函数图象会越来越靠近y轴,但永远不会与y轴相交.
(2)建立分类讨论的思想.在画对数函数图象之前要先判断对数的底数a的取值范围是a>1,还是0
例4 画出函数y=lg|x-1|的图象.
例5
(1)函数y=x+a与y=logax的图象只可能是下图中的( )
(2)函数y=loga(x+1)-2(a>0,且a≠1)的图象恒过点________.
[跟踪训练]
3
(1)
已知a>0,且a≠1,则函数y=ax与y=loga(-x)的图象只能是( )
(2)y=loga+2图象恒过定点坐标是________.
例6.已知函数y=lg(ax2+2ax+1):
(1)若函数的定义域为R,求a的取值范围;
(2)若函数的值域为R,求a的取值范围.
(1)对数函数图像必经过第一、四象限,在第一象限的规律是:
以直线把第一象限分成两个区域,每个区域里对数函数底数都是由左向右逐渐增大,如右图所示,,,,对应,,,,则;
(2)与关于轴对称;
(3)轴是渐进线,即图像向上、下无限延伸;
1.思考辨析
1.下列函数中,是对数函数的是( )
A.y=logxa(x>0且x≠1)
B.y=log2x-1
C.y=2lg8x
D.y=log5x
2.已知对数函数的图象过点M(9,2),则此对数函数的解析式为( )
A.y=log2x
B.y=log3x
C.y=x
D.y=x
3.函数f(x)=+lg(x+1)的定义域为( )
A.[-1,3)
B.(-1,3)
C.(-1,3]
D.[-1,3]
4.已知函数f(x)=log3(x+1),若f(a)=1,则a等于( )
A.0
B.1
C.2
D.3
5.函数y=lg(x+1)的图象大致是( )
6.图中曲线是对数函数的图象,已知取,,,四个值,则相应于,,,的值依次为
A.,,,
B.,,,
C.,,,
D.,,,
7.设则(
)
A.a>b>c
B.a>c>b
C.b>a>c
D.b>c>a
8.满足“对定义域内任意实数x,y,都有f(xy)=f(x)+f(y)”的函数f(x)可以是( )
A.f(x)=x2
B.f(x)=2x
C.f(x)=log2x
D.f(x)=elnx
9.如果函数y=log2x的图象经过点A(4,y0),那么y0=____.
10.函数y=(3x-2)的定义域是____.
11.已知函数y=loga(x-3)-1的图象恒过定点P,则点P的坐标是________.
12.已知函数f(x)=lg(x2+ax+1)的定义域是R,则实数a的取值范围是_______.
13.函数f(x)=的图象如图所示,则a+b+c=___.
14..已知对数函数f(x)=(m2-m-1)log(m+1)x,求f(27).
15.已知f(x)=lg,x∈(-1,1),若f(a)=,求f(-a).
16.求下列各式中x的取值范围:
(1);(2);(3).
17.比较下列各组值的大小:
(1),;(2)log1.51.6,log1.51.4;(3)log0.57,log0.67;(4)log3π,log20.8.
18..已知函数f(x)=(1)求f?的值;(2)若f(a)=,求a的值.
19.若函数的定义域为一切实数,求实数的取值范围.
1.下列函数中,是对数函数的是( )
A.y=logxa(x>0且x≠1)
B.y=log2x-1
C.y=2lg8x
D.y=log5x
2.已知对数函数的图象过点M(9,2),则此对数函数的解析式为(
)
A.y=log2x
B.y=log3x
C.y=x
D.y=x
3.函数f(x)=ln(1-x)的定义域是(
)
A.(0,1)
B.[0,1)
C.(1,+∞)
D.(-∞,1)
4.y=2x与y=log2x的图象关于(
)
A.x轴对称
B.直线y=x对称
C.原点对称
D.y轴对称
5.设a=log32,b=log52,c=log23,则(
D )
A.a>c>b
B.b>c>a
C.c>b>a
D.c>a>b
6.函数y=loga(3x-2)+2(a>0,且a≠1)的图象必过定点(
)
A(1,2)
B
(2,2)
C
(2,3)
D
(,2)
7.
如果函数y=log2x的图象经过点A(4,y0),那么y0=
.
8.设ln
b>ln
a>ln
c,则a,b,c的大小关系为
.
9.若函数f(x)=logax(0
②y=logax2(a>0,且a≠1);③y=lox;
④y=log3x;⑤y=logx(x>0,且x≠1);
⑥y=lox.其中是对数函数的为(
)
A③④⑤
B②④⑥
C①③⑤⑥
D③⑥
11.已知函数f(x)=loga(x+2),若其图象过点(6,3),则f(2)的值为( )
A.-2
B.2
C.
D.-
12.函数y=+lg(2x+1)的定义域( )
A.(,3]
B.(,3)
C.(-,3]
D.(-,3)
13.已知函数f(x)=ln
x,g(x)=lg
x,h(x)=log3x,直线y=a(a<0)与这三个函数的交点的横坐标分别是x1,x2,x3,则x1,x2,x3的大小关系是( )
A.
x2
x1
x1
x3
)
15.若loga<1,则a的取值范围为
.
16.若对数函数f(x)=(a2-2a-2)logax,则f(9)=
.
17.求下列函数的定义域:
(1)y=log5(1-x);(2)y=log(3x-1)5;(3)y=.
18.比较下列各组数的大小;
(1)log0.90.8,log0.90.7,log0.80.9;
(2)log32,log23,log4.
题型一
对数函数的概念
注意:判断一个函数是对数函数必须是形如y=logax(a>0且a≠1)的形式,即必须满足以下条件:
(1)系数为1.(2)底数为大于0且不等于1的常数.(3)对数的真数仅有自变量x.
例1
指出下列函数哪些是对数函数?
(1)y=3log2x;(2)y=log6x;
(3)y=logx3;(4)y=log2x+1.
(1)log2x的系数是3,不是1,不是对数函数.
(2)符合对数函数的结构形式,是对数函数.
(3)自变量在底数位置上,不是对数函数.
(4)对数式log2x后又加1,不是对数函数.
[跟踪训练]1(1)对数函数的图象过点M(16,4),则此对数函数的解析式为
(2)若对数函数y=f(x)满足f(4)=2,则该对数函数的解析式为( )
A.y=log2x
B.y=2log4x
C.y=log2x或y=2log4x
D.不确定
(1)
y=log2x
[解析] 设对数函数为y=logax,则4=loga16,∴a4=16,
∴a=2,∴y=log2x.
(2)A
[解析] 设对数函数的解析式为y=logax(a>0,且a≠1),由题意可知loga4=2,
∴a2=4,∴a=2.
∴该对数函数的解析式为y=log2x.
题型二 对数型函数的定义域
注意:求与对数函数有关的函数定义域时,除遵循前面已学习过的求函数定义域的方法外,还要对这种函数自身有如下要求:一是要特别注意真数大于零;二是要注意对数的底数大于零且不等于1.
例2 求下列函数的定义域.
(1)y=loga(3-x)+loga(3+x);
(2)y=log2(16-4x).
解 (1)由得-3
(2)由16-4x>0,得4x<16=42,
由指数函数的单调性得x<2,
∴函数y=log2(16-4x)的定义域为(-∞,2).
[跟踪训练]2
求下列函数的定义域.
(1)y=;(2)y=;
(3)y=;(4)y=log(x+1)(2-x).
(1)定义域为(0,+∞).
(2)由解得
例3
比较下列各组中两个值的大小:
(1)log31.9,log32;
(2)log23,log0.32;
(3)logaπ,loga3.14(a>0,a≠1).
解 (1)因为y=log3x在(0,+∞)上是增函数,所以log31.9
(3)当a>1时,函数y=logax在(0,+∞)上是增函数,则有logaπ>loga3.14;
当0
A.loga5.1
C.log1.1(a+1)
题型四
对数函数的图象
注意:(1)明确图象的分布区域.对数函数的图象在第一、四象限.当x趋近于0时,函数图象会越来越靠近y轴,但永远不会与y轴相交.
(2)建立分类讨论的思想.在画对数函数图象之前要先判断对数的底数a的取值范围是a>1,还是0
例4 画出函数y=lg|x-1|的图象.
解 (1)先画出函数y=lg
x的图象(如图).
(2)再画出函数y=lg|x|的图象(如图).
(3)最后画出函数y=lg|x-1|的图象(如图).
例5
(1)函数y=x+a与y=logax的图象只可能是下图中的( )
(2)函数y=loga(x+1)-2(a>0,且a≠1)的图象恒过点________.
(1) C
(2)(0,-2)
因为函数y=logax
(a>0,且a≠1)的图象恒过点(1,0),则令x+1=1得x=0,此时y=loga(x+1)-2=-2,所以函数y=loga(x+1)-2(a>0,且a≠1)的图象恒过点(0,-2).
[跟踪训练]
3
(1)
已知a>0,且a≠1,则函数y=ax与y=loga(-x)的图象只能是( )
(2)y=loga+2图象恒过定点坐标是________.
(1)
B
若0
(2)(-2,2)
[解析] 令=1,得x=-2,此时y=2,∴函数y=loga+2过定点(-2,2).
例6.已知函数y=lg(ax2+2ax+1):
(1)若函数的定义域为R,求a的取值范围;
(2)若函数的值域为R,求a的取值范围.
【分析】(1)由于函数的定义域为R,可得ax2+2ax+1>0恒成立.当a=0时,显然成立,当a≠0时,应有a>0且△=4a2﹣4a<0,由此求得a的取值范围.
(2)若函数的值域为R,则ax2+2ax+1能取遍所有的正整数,故有
a>0且△=4a2﹣4a≥0,由此求得a的取值范围.
【解答】解:(1)∵函数的定义域为R,∴ax2+2ax+1>0恒成立.当a=0时,显然成立.
当a≠0时,应有a>0且△=4a2﹣4a<0,解得
a<1.
故a的取值范围为[0,1).
(2)若函数的值域为R,则ax2+2ax+1能取遍所有的正整数,∴a>0且△=4a2﹣4a≥0.
解得
a≥1,故a的取值范围为[1,+∞).
(1)对数函数图像必经过第一、四象限,在第一象限的规律是:
以直线把第一象限分成两个区域,每个区域里对数函数底数都是由左向右逐渐增大,如右图所示,,,,对应,,,,则;
(2)与关于轴对称;
(3)轴是渐进线,即图像向上、下无限延伸;
1.思考辨析
1.下列函数中,是对数函数的是( D )
A.y=logxa(x>0且x≠1)
B.y=log2x-1
C.y=2lg8x
D.y=log5x
[解析] A、B、C都不符合对数函数的定义,故选D.
2.已知对数函数的图象过点M(9,2),则此对数函数的解析式为( B )
A.y=log2x
B.y=log3x
C.y=x
D.y=x
[解析] 设对数函数为y=logax,则2=loga9,
∴a2=9,∴a=3,∴y=log3x,故选B.
3.函数f(x)=+lg(x+1)的定义域为( )C
A.[-1,3)
B.(-1,3)
C.(-1,3]
D.[-1,3]
4.已知函数f(x)=log3(x+1),若f(a)=1,则a等于( )C
A.0
B.1
C.2
D.3
5.函数y=lg(x+1)的图象大致是( )C
6.图中曲线是对数函数的图象,已知取,,,四个值,则相应于,,,的值依次为
A.,,,
B.,,,
C.,,,
D.,,,
【答案】A
【解析】
由已知中曲线是对数函数的图象,
由对数函数的图象和性质,可得,,,的值从小到大依次为:,,,,
由取,,,四个值,
故,,,的值依次为,,,,
故选:.
7.设则(
)
A.a>b>c
B.a>c>b
C.b>a>c
D.b>c>a
【答案】A
【解析】
,
.
故选:A.
8.满足“对定义域内任意实数x,y,都有f(xy)=f(x)+f(y)”的函数f(x)可以是( C )
A.f(x)=x2
B.f(x)=2x
C.f(x)=log2x
D.f(x)=elnx
[解析] ∵对数运算律中有logaM+logaN=loga(MN),
∴f(x)=log2x满足题目要求.
9.如果函数y=log2x的图象经过点A(4,y0),那么y0=__2__.
[解析] 将A(4,y0)代入y=log2x得log24=y0,∴y0=2.
10.函数y=(3x-2)的定义域是__(,+∞)__.
[解析] 由3x-2>0得x>,所以函数的定义域为(,+∞).
11.已知函数y=loga(x-3)-1的图象恒过定点P,则点P的坐标是________.
(4,-1)
[解析] y=logax的图象恒过点(1,0),令x-3=1,得x=4,则y=-1.
12.已知函数f(x)=lg(x2+ax+1)的定义域是R,则实数a的取值范围是__(-2,2)__.
[解析] 由题意知x2+ax+1>0恒成立,所以Δ=a2-4<0,即-2
[解析] 由题图可求得直线的方程为y=2x+2,即a=2,b=2,又函数y=logc的图象过点(0,2),将其坐标代入可得c=,所以a+b+c=2+2+=.
14..已知对数函数f(x)=(m2-m-1)log(m+1)x,求f(27).
[解析] ∵f(x)是对数函数,∴,
解得m=2.
∴f(x)=log3x,∴f(27)=log327=3.
15.已知f(x)=lg,x∈(-1,1),若f(a)=,求f(-a).
[解析] 解法一:∵f(-x)=lg=lg()-1=-f(x),∴f(-a)=-f(a)=-.
解法二:f(a)=lg,
f(-a)=lg=lg()-1=-lg=-.
16.求下列各式中x的取值范围:
(1);
(2);
(3).
(1),,解得:或,
的取值范围是.
(2)
,解得:,
的取值范围是.
(3)
,解得:,
的取值范围是.
17.比较下列各组值的大小:
(1),;
(2)log1.51.6,log1.51.4;
(3)log0.57,log0.67;
(4)log3π,log20.8.
18..已知函数f(x)=(1)求f?的值;(2)若f(a)=,求a的值.
解 (1)∵f?=log3=-3,∴f?=f(-3)=2-3=.
(2)当a>0时,由f(a)=,得log3a=.∴a==.
当a≤0时,由f(a)=,得2a=,∴a=-1,
综上所述a的值为-1或.
19.若函数的定义域为一切实数,求实数的取值范围.
解析:因为函数的定义域为一切,
等价于,对任意的实数恒成立.
当时,,符合条件.
当时,.
综上.
故答案为:
1.下列函数中,是对数函数的是( )
A.y=logxa(x>0且x≠1)
B.y=log2x-1
C.y=2lg8x
D.y=log5x
2.已知对数函数的图象过点M(9,2),则此对数函数的解析式为(
)
A.y=log2x
B.y=log3x
C.y=x
D.y=x
3.函数f(x)=ln(1-x)的定义域是(
)
A.(0,1)
B.[0,1)
C.(1,+∞)
D.(-∞,1)
4.y=2x与y=log2x的图象关于(
)
A.x轴对称
B.直线y=x对称
C.原点对称
D.y轴对称
5.设a=log32,b=log52,c=log23,则(
D )
A.a>c>b
B.b>c>a
C.c>b>a
D.c>a>b
6.函数y=loga(3x-2)+2(a>0,且a≠1)的图象必过定点(
)
A(1,2)
B
(2,2)
C
(2,3)
D
(,2)
7.
如果函数y=log2x的图象经过点A(4,y0),那么y0=
.
8.设ln
b>ln
a>ln
c,则a,b,c的大小关系为
.
9.若函数f(x)=logax(0
②y=logax2(a>0,且a≠1);③y=lox;
④y=log3x;⑤y=logx(x>0,且x≠1);
⑥y=lox.其中是对数函数的为(
)
A③④⑤
B②④⑥
C①③⑤⑥
D③⑥
11.已知函数f(x)=loga(x+2),若其图象过点(6,3),则f(2)的值为( )
A.-2
B.2
C.
D.-
12.函数y=+lg(2x+1)的定义域( )
A.(,3]
B.(,3)
C.(-,3]
D.(-,3)
13.已知函数f(x)=ln
x,g(x)=lg
x,h(x)=log3x,直线y=a(a<0)与这三个函数的交点的横坐标分别是x1,x2,x3,则x1,x2,x3的大小关系是( )
A.
x2
x1
x1
x3
)
15.若loga<1,则a的取值范围为
.
16.若对数函数f(x)=(a2-2a-2)logax,则f(9)=
.
17.求下列函数的定义域:
(1)y=log5(1-x);
(2)y=log(3x-1)5;
(3)y=.
18.比较下列各组数的大小;
(1)log0.90.8,log0.90.7,log0.80.9;
(2)log32,log23,log4.
【参考答案】
1.
D
[解析]
A、B、C都不符合对数函数的定义,故选D.
2.
B
[解析]设对数函数为y=logax,则2=loga9,∴a2=9,∴a=3,∴y=log3x,故选B.
3.
D
[解析]由1-x>0得x<1,故选D.
4.
B
解析]函数y=2x与函数y=log2x是互为反函数,故它们的图象关于直线y=x对称.
5.
D
解析]
a=log32
A
解析:令3x-2=1,得x=1,又loga(3×1-2)+2=2,故定点为(1,2),选A.
7.
2
[解析] 将A(4,y0)代入y=log2x得log24=y0,∴y0=2.
8.
b>a>c
解析:由对数函数的图象与性质可知,函数y=ln
x在(0,+∞)上为单调递增函数,因为ln
b>ln
a>ln
c,所以b>a>c.
9.[解析] 由题意得f(x)max=logaa=1,f(x)min=loga(2a)=1+loga2,∴1=3×(1+loga2),∴a=.
10.
D
解析:①②④不满足对数函数解析式特征,⑤中真数是常数,故只有③⑥是对数函数.选D.
11.
B
[解析] 由题意得3=loga8,∴a3=8,∴a=2.∴f(x)=log2(x+2),∴f(2)=log24=2.
12.
D
[解析] 由题意得,∴-
解析:令a=-1,得ln
x1=-1,lg
x2=-1,log3x3=-1,故x1=,x2=,x3=,则x1>x3>x2.选A.
14.
A
解析:函数y=log2|x|为偶函数,且x>0时,y=log2x,故选A.
15.
0<a<或a>1
解析 loga<1即loga<logaa,当a>1时,函数y=logax在定义域内是增函数,所以loga<logaa总成立;
当0<a<1时,函数y=logax在定义域内是减函数,由loga<logaa,得a<,故0<a<.
故a的取值范围为0<a<或a>1.
解析:由对数函数定义知故a=3或a=-1(舍去),则f(x)=log3x,故f(9)=log39=2.
17 (1)要使函数式有意义,需1-x>0,解得x<1,
所以函数y=log5(1-x)的定义域是{x|x<1}.
(2)要使函数式有意义,需
解得x>,且x≠,
所以函数y=log(3x-1)5的定义域是.
(3)要使函数式有意义,需
解得x<4,且x≠3,
所以函数y=的定义域是{x|x<4,且x≠3}.
18.(1)log0.80.9<log0.90.8<log0.90.7;(2)log4<log32<log23
【解析】(1)因为y=log0.9x在(0,+∞)上是减函数,且0.9>0.8>0.7,所以1<log0.90.8<log0.90.7.
又因为log0.80.9<log0.80.8=1,所以log0.80.9<log0.90.8<log0.90.7.
(2)由log31<log32<log33,得0<log32<1.
又因为log23>log22=1,log4<log41=0,所以log4<log32<log23.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
