4.3 对数学案

1、对数的定义
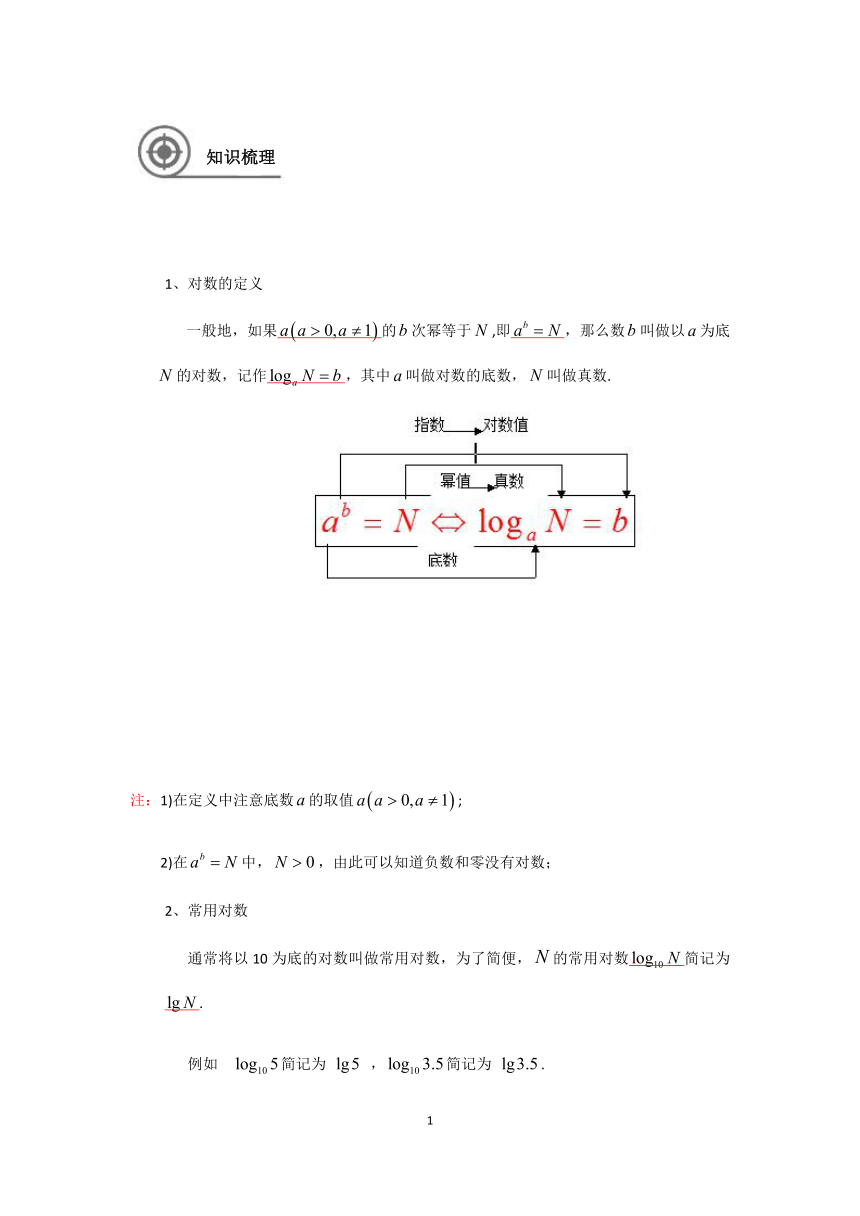
一般地，如果的次幂等于,即，那么数叫做以为底的对数，记作，其中叫做对数的底数，叫做真数.
注：1)在定义中注意底数的取值;
2)在中，，由此可以知道负数和零没有对数；
2、常用对数
通常将以10为底的对数叫做常用对数，为了简便，的常用对数简记为.
例如
简记为
，简记为
.
3、自然对数
在科学技术中常常使用无理数为底的对数，以为底的对数叫做自然对数，为了简便，的常用对数简记为.
对数计算公式
（1）基本公式：
运算性质：
如果且，，那么
1、；
积的对数
=
对数的和
2、；
商的对数=对数的差
3、．
一个数次方的对数=这个数对数的倍
4.
（3）公式延伸
1、
（换底公式）
2、
3、
题型一　指数式与对数式的互化
(1)指数式化为对数式：将指数式的幂作为真数，指数作为对数，底数不变，写出对数式.
(2)对数式化为指数式：将对数式的真数作为幂，对数作为指数，底数不变，写出指数式.
例1　根据对数定义，将下列指数式写成对数式：
①3x＝；　　　　
②x＝64；
③log16＝－；
④ln
10＝x.
[跟踪训练]1
将下列指数式化为对数式，对数式化为指数式：
(1)43＝64；(2)ln
a＝b；(3)＝n；(4)lg
1000＝3.
题型二　利用指数式与对数式的互化求变量的值
方法:①将对数式化为指数式，构建方程转化为指数问题.
②利用幂的运算性质和指数的性质计算.
例2
利用指数式、对数式的互化求下列各式中x的值.
(1)log2x＝－；(2)logx25＝2；(3)log5x2＝2.
[跟踪训练]
2
(1)求下列各式的值.
①log981＝________.②log0.41＝________.③ln
e2＝________.
(2)求下列各式中x的值.
①log64x＝－；②logx8＝6；
③lg
100＝x；④－ln
e2＝x.
题型三　对数基本性质的应用
利用对数性质求值的方法：
(1)性质
loga1＝0
logaa＝1
(a>0，且a≠1).
(2)求多重对数式的值的解题方法是由内到外，如求loga(logbc)的值，先求logbc的值，再求loga(logbc)的值．
例3
求下列式子值。
(1)2log23＋2log31－3log77＋3ln
1＝________.
(2)9＝________；
[跟踪训练]
3化简求值　
(1)71－log75；(2)100；(3)alogab·logbc(a，b为不等于1的正数，c>0).
例4　求下列各式中的x的值．
(1)log2(log3x)＝0；
(2)log5(log2x)＝1；
[跟踪训练]
4　求下列各式中的x的值．
log8[log7(log2x)]＝0；
(2)log2[log3(log2x)]＝1.
题型四
数值计算
例5．
计算（1），
（2），
（3），
（4）
例6．计算：(1)
(2)
(3)
题型五
含字母的对数计算
例7．
用，，表示下列各式：
．
[跟踪训练]
5.若a>0且a≠1，x>0，n∈N
，则下列各式正确的是(　　)
A．logax＝－loga
B．(logax)n＝nlogax
C．(logax)n＝logaxn
D．logax＝loga
题型六
换底公式灵活应用
例8
(1)求的值；
计算的值
例9
(1)设3x＝4y＝36，求＋的值
(2)已知，求
(3)已知2x＝3y＝5z，且＋＋＝1，求x，y，z.
利用对数运算性质化简与求值的原则和方法
(1)基本原则：
①正用或逆用公式，对真数进行处理，②选哪种策略化简，取决于问题的实际情况，一般本着便于真数化简的原则进行.
(2)两种常用的方法：
①“收”，将同底的两对数的和(差)收成积(商)的对数；
②“拆”，将积(商)的对数拆成同底的两对数的和(差).
一、单选题
1．如果，则有（
）
A．
B．
C．
D．
2．log5＋log53等于（
）
A．0
B．1
C．－1
D．log5
3．方程的解是（
）
A．
B．
C．x＝1
D．x＝2
4．若实数a，b满足，则（
）
A．
B．
C．
D．1
5．在N＝log(5－b)(b－2)中，实数b的取值范围是(　　)
A．b<2或b>5
B．2C．4D．26．若，则x＋y＋z的值为(　　)
A．9
B．8
C．7
D．6
7．设a，b，c均为不等于1的正实数，则下列等式中恒成立的是（
）
A．logab·logcb＝logca
B．logab·logca＝logcb
C．loga(bc)＝logab·logac
D．loga(b＋c)＝logab＋logac
8．化简的结果是（
）
A．
B．1
C．2
D．4
9．2等于(　　)
A．2＋
B．2
C．2＋
D．1＋
10．设，且，则
(
)
A．
B．10
C．20
D．100
二、多选题
11．下列等式不成立的是(
)
A．
B．
C．
D．
E.
12．已知，均为正实数，若，，则（
）
A．
B．
C．
D．2
13．若，，则（
）
A．
B．
C．
D．
三、填空题
14.若，则________.
15.已知实数满足，且，且_____.
16.若，则________.
17.___________，______.
18.已知，则______；_______.
19.计算：__________，_________.
四、解答题
20.计算下列各式：
（1）；
（2）；
（3）；
（4）lg(＋).
21.（1）证明对数换底公式：（其中且，且，）
（2）已知，试用表示.
22.设3x＝4y＝6z＝t>1，求证：－＝.
1．log5＋log53等于（
）
A．0
B．1
C．－1
D．log5
2．设a，b，c均为不等于1的正实数，则下列等式中恒成立的是（
）
A．logab·logcb＝logca
B．logab·logca＝logcb
C．loga(bc)＝logab·logac
D．loga(b＋c)＝logab＋logac
3．logbN＝a(b>0，b≠1，N>0)对应的指数式是（
）
A．ab＝N
B．ba＝N
C．aN＝b
D．bN＝a
4．若，则等于（
）．
A．
B．
C．
D．
5．设，则实数的值为（
）
A．
B．
C．
D．
6.(多选)若，，则（
）
A．
B．
C．
D．
7.若，则________.
8.若，则的值是
．
9.十六、十七世纪之交，随着天文、航海、工程、贸易及军事的发展，改进数字计算方法成了当务之急，约翰·纳皮尔正是在研究天文学的过程中，为了简化其中的计算而发明了对数，后来天才数学家欧拉发现了对数与指数的关系，即．现已知，则________，________
10.计算：（1）.
（2）.
11.已知，求证：.
12.已知（1）求的值；（2）求的值.
题型一　指数式与对数式的互化
(1)指数式化为对数式：将指数式的幂作为真数，指数作为对数，底数不变，写出对数式.
(2)对数式化为指数式：将对数式的真数作为幂，对数作为指数，底数不变，写出指数式.
例1　根据对数定义，将下列指数式写成对数式：
①3x＝；　　　　
②x＝64；
③log16＝－；
④ln
10＝x.
(1)①log3＝x；②log64＝x；③16＝；④ex＝10.
[跟踪训练]1
将下列指数式化为对数式，对数式化为指数式：
(1)43＝64；(2)ln
a＝b；(3)＝n；(4)lg
1000＝3.
解　(1)因为43＝64，所以log464＝3；
(2)因为ln
a＝b，所以eb＝a；
(3)因为＝n，所以logn＝m；
(4)因为lg
1
000＝3，所以103＝1
000.
题型二　利用指数式与对数式的互化求变量的值
方法:①将对数式化为指数式，构建方程转化为指数问题.
②利用幂的运算性质和指数的性质计算.
例2
利用指数式、对数式的互化求下列各式中x的值.
(1)log2x＝－；(2)logx25＝2；(3)log5x2＝2.
解　(1)由log2x＝－，得2－＝x，∴x＝.
(2)由logx25＝2，得x2＝25.∵x＞0，且x≠1，∴x＝5.
(3)由log5x2＝2，得x2＝52，∴x＝±5.∵52＝25＞0，(－5)2＝25＞0，∴x＝5或x＝－5.
[跟踪训练]
2
(1)求下列各式的值.
①log981＝________.②log0.41＝________.③ln
e2＝________.
(1)①2　②0　③2
解析　①设log981＝x，所以9x＝81＝92，故x＝2，即log981＝2；②设log0.41＝x，所以0.4x＝1＝0.40，故x＝0，即log0.41＝0；③设ln
e2＝x，所以ex＝e2，故x＝2，即ln
e2＝2.
(2)求下列各式中x的值.
①log64x＝－；②logx8＝6；
③lg
100＝x；④－ln
e2＝x.
解　①由log64x＝－得x＝64－＝43×(－)＝4－2＝；
②由logx8＝6，得x6＝8，又x>0，即x＝8＝23×＝；
③由lg
100＝x，得10x＝100＝102，即x＝2；
④由－ln
e2＝x，得ln
e2＝－x，所以e－x＝e2，所以－x＝2，即x＝－2.
题型三　对数基本性质的应用
利用对数性质求值的方法：
(1)性质
loga1＝0
logaa＝1
(a>0，且a≠1).
(2)求多重对数式的值的解题方法是由内到外，如求loga(logbc)的值，先求logbc的值，再求loga(logbc)的值．
例3
求下列式子值。
(1)2log23＋2log31－3log77＋3ln
1＝________.
(2)9＝________；
(1)
0
解析　原式＝3＋2×0－3×1＋3×0＝0.
(2)4
解析
9＝(9)＝3＝4.
[跟踪训练]
3化简求值　
(1)71－log75；(2)100；
(3)alogab·logbc(a，b为不等于1的正数，c>0).
解　(1)原式＝7×7－log75＝＝.
(2)原式＝100lg
9×100－lg
2＝10lg
9×＝9×＝9×＝.
(3)原式＝(alogab)logbc＝blogbc＝c.
例4　求下列各式中的x的值．
(1)log2(log3x)＝0；
(2)log5(log2x)＝1；
解析　(1)因为log2(log3x)＝0，所以log3x＝1，所以x＝3.
(2)因为log5(log2x)＝1，所以log2x＝5，所以x＝25＝32.
[跟踪训练]
4
[跟踪训练]
4　求下列各式中的x的值．
(1)log8[log7(log2x)]＝0；
(2)log2[log3(log2x)]＝1.
解析：(1)由log8[log7(log2x)]＝0得log7(log2x)＝1，所以log2x＝7，所以x＝27＝128.
(2)由log2[log3(log2x)]＝1得log3(log2x)＝2，所以log2x＝32，所以x＝29＝512.
题型四
数值计算
例5．
计算
（1），
（2），
（3），
（4）
解：（1）25=
=2
（2）1=0．
（3）（×25）=
+
=
+
=
2×7+5=19．
（4）lg=．
例6．计算：
(1)
(2)
(3)
解：(1)
＝＝
＝＝＝1；
(2)
＝＝＝2；
(3)解法一：lg14-2lg+lg7-lg18
=lg(2×7)-2(lg7-lg3)+lg7-lg(×2)
=lg2+lg7-2lg7+2lg3+lg7-2lg3-lg2=0．?
解法二：lg14-2lg+lg7-lg18
=lg14-lg+lg7-lg18
=
评述：此例题体现对数运算性质的综合运用，应注意掌握变形技巧，如(3)题各部分变形要化到最简形式，同时注意分子、分母的联系.(2)题要避免错用对数运算性质.
题型五
含字母的对数计算
例7．
用，，表示下列各式：
．
解：（1）=（xy）-z=x+y-
z
（2）=（
=
+=2x+．
[跟踪训练]
5.若a>0且a≠1，x>0，n∈N
，则下列各式正确的是(　　)
A．logax＝－loga
B．(logax)n＝nlogax
C．(logax)n＝logaxn
D．logax＝loga
答案　A
题型六
换底公式灵活应用
例8
(1)求的值；
分析：利用换底公式统一底数；
解法（1）：原式=
解法（2）：原式=
(2)计算的值
分析：先利用对数运算性质法则和换底公式进行化简，然后再求值；
解：原式=
例9
(1)设3x＝4y＝36，求＋的值
(1)由已知分别求出x和y.
∵3x＝36,4y＝36，
∴x＝log336，y＝log436，
由换底公式得：
x＝＝，y＝＝，
∴＝log363，＝log364，
∴＋＝2log363＋log364
（2）已知，求
∵log189＝a,18b＝5，∴log185＝b.
∴log3645＝＝
＝＝＝.
(3)已知2x＝3y＝5z，且＋＋＝1，求x，y，z.
令2x＝3y＝5z＝k(k>0)，
∴x＝log2k，y＝log3k，z＝log5k，
∴＝logk2，＝logk3，＝logk5，
由＋＋＝1，得logk2＋logk3＋logk5＝logk30＝1，
∴k＝30，
∴x＝log230＝1＋log215，y＝log330＝1＋log310，z＝log530＝1＋log56.
利用对数运算性质化简与求值的原则和方法
(1)基本原则：
①正用或逆用公式，对真数进行处理，②选哪种策略化简，取决于问题的实际情况，一般本着便于真数化简的原则进行.
(2)两种常用的方法：
①“收”，将同底的两对数的和(差)收成积(商)的对数；
②“拆”，将积(商)的对数拆成同底的两对数的和(差).
一、单选题
1．如果，则有（
）
A．
B．
C．
D．
【答案】C
【解析】
利用指数化对数得可，
故选：C．
2．log5＋log53等于（
）
A．0
B．1
C．－1
D．log5
【答案】A
【解析】
因为.
故选：A.
3．方程的解是（
）
A．
B．
C．x＝1
D．x＝2
【答案】B
【解析】
因为，所以，
所以，所以.
故选：B.
4．若实数a，b满足，则（
）
A．
B．
C．
D．1
【答案】D
【解析】
因为，所以，
．
故选：D．
5．在N＝log(5－b)(b－2)中，实数b的取值范围是(　　)
A．b<2或b>5
B．2C．4D．2【答案】D
【解析】
由对数的意义得，解得且。
所以实数b的取值范围是且。选D。
6．若，则x＋y＋z的值为(　　)
A．9
B．8
C．7
D．6
【答案】A
【解析】
∵log2(log3x)＝0，
∴log3x＝1.
∴x＝3.
同理y＝4，z＝2.
∴x＋y＋z＝9.
故选A．
7．设a，b，c均为不等于1的正实数，则下列等式中恒成立的是（
）
A．logab·logcb＝logca
B．logab·logca＝logcb
C．loga(bc)＝logab·logac
D．loga(b＋c)＝logab＋logac
【答案】B
【解析】
由logab·logcb＝·≠logca，故A错；
由logab·logca＝·＝＝logcb.故正确；
对选项，，由对数的运算法则，容易知，其显然不成立.
故选：.
8．化简的结果是（
）
A．
B．1
C．2
D．4
【答案】C
【解析】
原式.
故选：C.
9．2等于(　　)
A．2＋
B．2
C．2＋
D．1＋
【答案】B
【解析】
.
故选B.
10．设，且，则
(
)
A．
B．10
C．20
D．100
【答案】A
【解析】
由得，所以，，故选A.
二、多选题
11．下列等式不成立的是(
)
A．
B．
C．
D．
E.
【答案】DE
【解析】
根据对数式的运算,可得,,故A?B成立;
由根式与指数式的互化可得,故C成立;
取,,发现D不成立;,故E不成立.
故选：DE
12．已知，均为正实数，若，，则（
）
A．
B．
C．
D．2
【答案】AD
【解析】
令，
则，
，，
或，
或
或
，代入得
或
，或，
．或
故选：AD.
13．若，，则（
）
A．
B．
C．
D．
【答案】ACD
【解析】
由，，得，，则
，
，
，
故正确的有：
故选：.
三、填空题
14.若，则________.
【答案】
【解析】
【分析】
设，则，结合对数的运算性质，即可求解.
【详解】
设，则，所以.
故答案为：.
15.已知实数满足，且，且_____.
【答案】
【解析】
，解得
故答案为：
16.若，则________.
【答案】
【解析】
由对数的换底公式，可得，
所以，所以.
故答案为：.
17.___________，______.
【答案】
【解析】
由对数的运算性质得，
由对数的换底公式可得.
故答案为：；.
18.已知，则______；_______.
【答案】
．
【解析】
，∴，故，
可化为，也就是，所以，
故，所以，解得.
故答案为：．
19.计算：__________，_________.
【答案】2
2
【解析】
，
，
，
.
.
故答案为：①2；②2.
四、解答题
20.计算下列各式：
（1）；
（2）；
（3）；
（4）lg(＋).
【答案】（1）；（2）－1；（3）1；（4）.
【解析】
（1）原式＝；
（2）原式＝；
（3）原式＝.
（4）原式＝＋＝＝＝.
21.（1）证明对数换底公式：（其中且，且，）
（2）已知，试用表示.
【答案】（1）证明见解析；（2）.
【解析】
（1）设，写成指数式.
两边取以为底的对数，得.
因为，，，因此上式两边可除以，得.
所以，.
（2）.
22.设3x＝4y＝6z＝t>1，求证：－＝.
证明　∵3x＝4y＝6z＝t，
∴x＝log3t，y＝log4t，z＝log6t，
∴＝logt3，＝logt4，＝logt6，
∴－＝logt6－logt3＝logt2.
又＝logt4＝2logt2，即＝logt2，
∴－＝.
1．log5＋log53等于（
）
A．0
B．1
C．－1
D．log5
【答案】A
【解析】因为.故选：A.
2．设a，b，c均为不等于1的正实数，则下列等式中恒成立的是（
）
A．logab·logcb＝logca
B．logab·logca＝logcb
C．loga(bc)＝logab·logac
D．loga(b＋c)＝logab＋logac
【答案】B
【解析】由logab·logcb＝·≠logca，故A错；
由logab·logca＝·＝＝logcb.故正确；
对选项，，由对数的运算法则，容易知，其显然不成立.故选：.
3．logbN＝a(b>0，b≠1，N>0)对应的指数式是（
）
A．ab＝N
B．ba＝N
C．aN＝b
D．bN＝a
【答案】B
【解析】由logbN＝a(b>0，b≠1，N>0)，则ba＝N故选：B
4．若，则等于（
）．
A．
B．
C．
D．
【答案】D
【解析】由，则.
故选：D
5．设，则实数的值为（
）
A．
B．
C．
D．
【答案】B
【解析】由题可知，故选：B
6.若，，则（
）
A．
B．
C．
D．
【答案】ACD
【解析】由，，得，，则
，，
，
故正确的有：。故选.
7.若，则________.
【答案】
【解析】，故.
故答案为：
8.若，则的值是
．
【答案】
【解析】∵，∴，则，故答案为．
9.十六、十七世纪之交，随着天文、航海、工程、贸易及军事的发展，改进数字计算方法成了当务之急，约翰·纳皮尔正是在研究天文学的过程中，为了简化其中的计算而发明了对数，后来天才数学家欧拉发现了对数与指数的关系，即．现已知，则________，________
【答案】
1
【解析】，，
；.
故答案为：；1
10.计算：（1）.
（2）.
【答案】（1）4；（2）.
【解析】（1）.
（2）
.
11.已知，求证：.
【答案】证明见解析；
【解析】令，
则，，，
所以.
12.已知
（1）求的值；
（2）求的值.
【答案】（1）-1（2）
【解析】由得，.
所以
；
由得，
所以.