人教版数学八年级上册 12.2三角形全等的判定同步测试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学八年级上册 12.2三角形全等的判定同步测试题(一)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 211.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 00:00:00 | ||
图片预览


文档简介
三角形全等的判定同步测试题(一)
一.选择题
1.给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,AC=EF,∠B=∠E;
③∠B=∠E,AB=DF,∠C=∠F;
④AB=DE,AC=DF,∠B=∠E.
其中,能确定△ABC和△DEF全等的条件共有( )
A.1组 B.2组 C.3组 D.4组
2.下列各组条件中,不能判定△ABC≌△DEF全等的是( )
A.AC=DF,AB=DE,BC=EF B.∠A=∠D,AC=DF,AB=DE
C.∠B=∠E,∠C=∠F,BC=EF D.∠A=∠D,BC=DF,∠B=∠E
3.如图,∠ABD=∠EBC,BC=BD,再添加一个条件,使得△ABC≌△EBD,所添加的条件不正确的是( )
A.∠A=∠E B.BA=BE C.∠C=∠D D.AC=DE
4.已知,在△ABC与△ADC中,AB=AD,那么添加一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.△ADC与△ABC的周长相等
5.根据下列已知条件,不能唯一画出△ABC的是( )
A.AB=5,BC=3,AC=6 B.AB=4,BC=3,∠A=50°
C.∠A=50°,∠B=60°,AB=4 D.AB=10,BC=20,∠B=80°
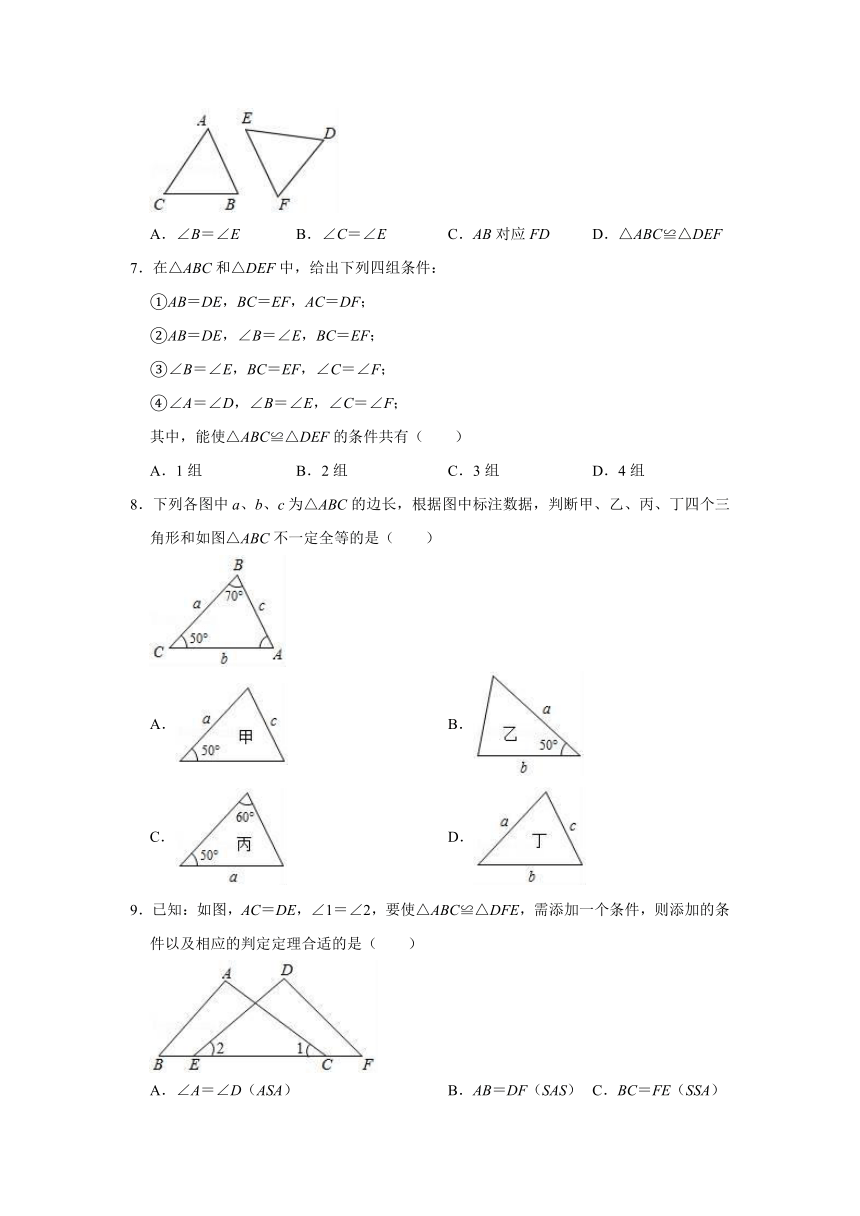
6.如图,两个三角形全等,且∠A=∠D,BC对应FE.则( )
A.∠B=∠E B.∠C=∠E C.AB对应FD D.△ABC≌△DEF
7.在△ABC和△DEF中,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④∠A=∠D,∠B=∠E,∠C=∠F;
其中,能使△ABC≌△DEF的条件共有( )
A.1组 B.2组 C.3组 D.4组
8.下列各图中a、b、c为△ABC的边长,根据图中标注数据,判断甲、乙、丙、丁四个三角形和如图△ABC不一定全等的是( )
A. B.
C. D.
9.已知:如图,AC=DE,∠1=∠2,要使△ABC≌△DFE,需添加一个条件,则添加的条件以及相应的判定定理合适的是( )
A.∠A=∠D(ASA) B.AB=DF(SAS) C.BC=FE(SSA) D.∠B=∠F(ASA)
10.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到△ABC≌△DEC,理由是( )
A.SSS B.AAS C.ASA D.SAS
二.填空题
11.已知平面直角坐标系中A(﹣2,1)、B(﹣2,﹣2)、C(4,﹣2),以 A、B、P为顶点的三角形与△ABC全等,写出所有符合条件的点P的坐标 .(点P不与点C重合)
12.如图,AB=AD,只要再添加一个条件: ,就可以通过“SSS”判定△ABC≌△ADC.
13.如图,已知:AD与BC交于O点,OA=OB,要使△AOC≌△BOD,添加一个你认为合适的条件为 .
14.如图,已知CB⊥AD,AE⊥CD,垂足分别为B,E,AE,BC相交于点F,AB=BC.若AB=8,CF=2,则BD= .
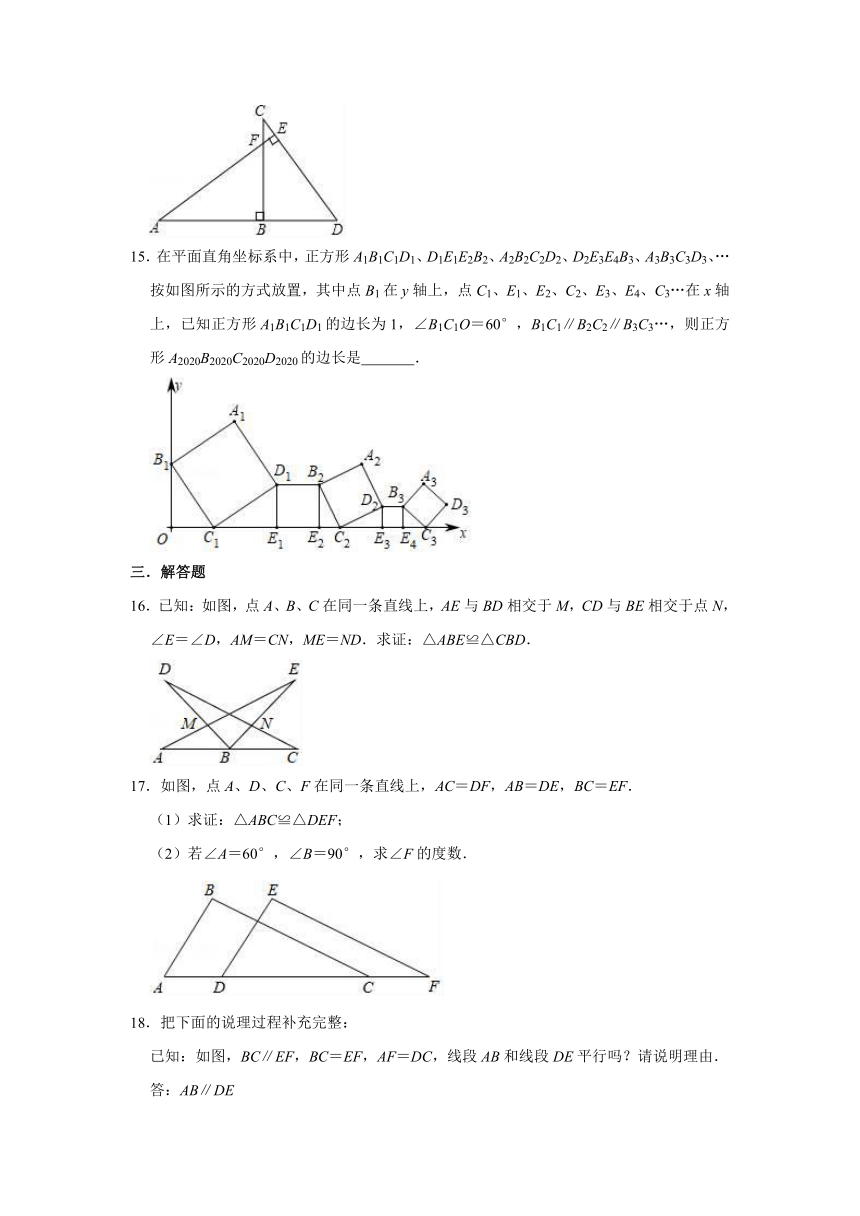
15.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3、…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2020B2020C2020D2020的边长是 .
三.解答题
16.已知:如图,点A、B、C在同一条直线上,AE与BD相交于M,CD与BE相交于点N,∠E=∠D,AM=CN,ME=ND.求证:△ABE≌△CBD.
17.如图,点A、D、C、F在同一条直线上,AC=DF,AB=DE,BC=EF.
(1)求证:△ABC≌△DEF;
(2)若∠A=60°,∠B=90°,求∠F的度数.
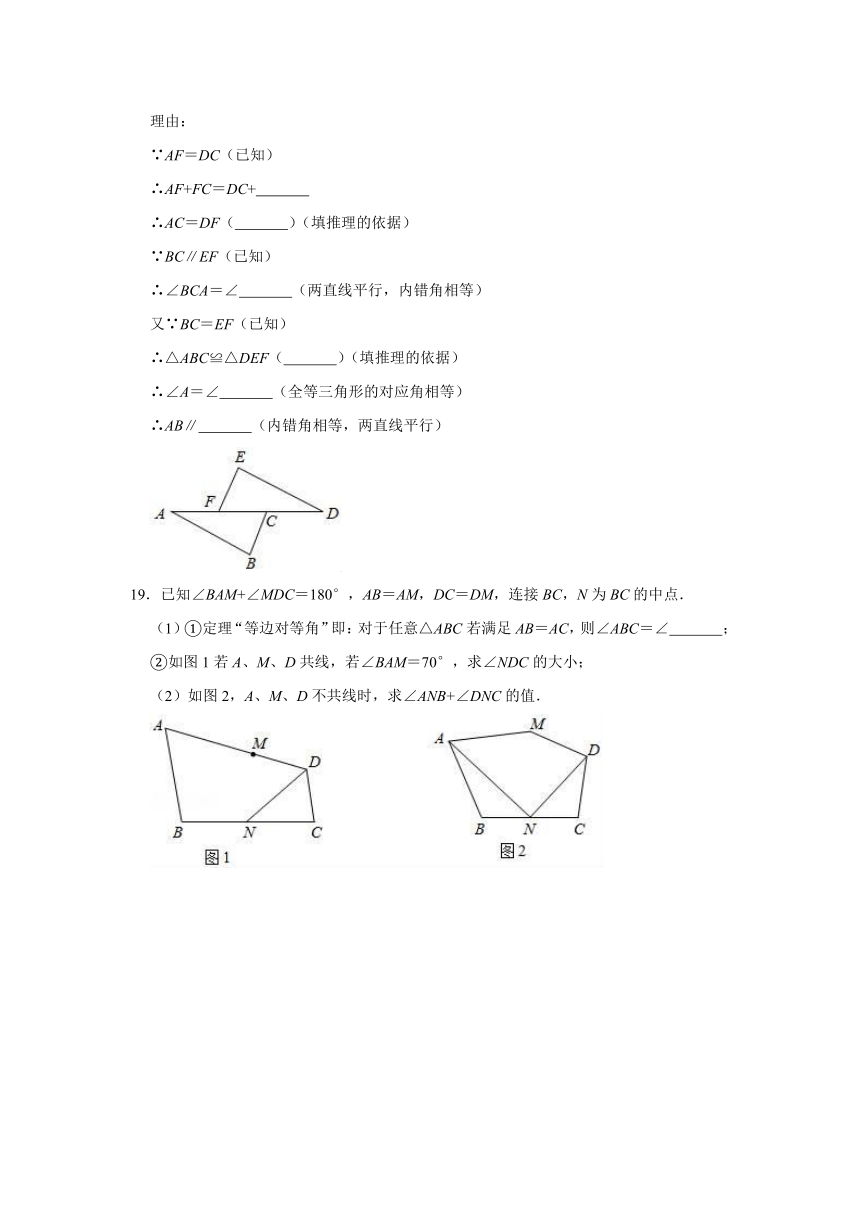
18.把下面的说理过程补充完整:
已知:如图,BC∥EF,BC=EF,AF=DC,线段AB和线段DE平行吗?请说明理由.
答:AB∥DE
理由:
∵AF=DC(已知)
∴AF+FC=DC+
∴AC=DF( )(填推理的依据)
∵BC∥EF(已知)
∴∠BCA=∠ (两直线平行,内错角相等)
又∵BC=EF(已知)
∴△ABC≌△DEF( )(填推理的依据)
∴∠A=∠ (全等三角形的对应角相等)
∴AB∥ (内错角相等,两直线平行)
19.已知∠BAM+∠MDC=180°,AB=AM,DC=DM,连接BC,N为BC的中点.
(1)①定理“等边对等角”即:对于任意△ABC若满足AB=AC,则∠ABC=∠ ;
②如图1若A、M、D共线,若∠BAM=70°,求∠NDC的大小;
(2)如图2,A、M、D不共线时,求∠ANB+∠DNC的值.
参考答案与试题解析
一.选择题
1.【解答】解:①AB=DE,BC=EF,AC=DF,可根据SSS判定△ABC≌△DEF;
②AB=DE,AC=EF,∠B=∠E,不能判定△ABC≌△DEF;
③∠B=∠E,AB=DF,∠C=∠F,不能判定△ABC≌△DEF;
④AB=DE,AC=DF,∠B=∠E,不能判定△ABC≌△DEF;
故选:A.
2.【解答】解:A、∵AC=DF,AB=DE,BC=EF,
∴利用SSS能推出△ABC≌△DEF,故本选项不符合题意;
B、∵∠A=∠D,AC=DF,AB=DE,
∴利用SAS能推出△ABC≌△DEF,故本选项不符合题意;
C、∵∠B=∠E,∠C=∠F,BC=EF,
∴利用ASA能推出△ABC≌△DEF,故本选项不符合题意;
D、∵∠A=∠D,BC=DF,∠B=∠E,BC和DF不是对应边,
∴不能推出△ABC≌△DEF,故本选项符合题意.
故选:D.
3.【解答】解:∵∠ABC=∠EBD,BC=BD,
∴当添加BA=BE时,可根据“SAS”判断△ABC≌△EBD;
当添加∠C=∠D时,可根据“ASA”判断△ABC≌△EBD;
当添加∠A=∠E时,可根据“AAS”判断△ABC≌△EBD.
故选:D.
4.【解答】解:A、∵在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),故本选项不合题意;
B、∵在△ABC和△ADC中,
,
∴△ABC≌△ADC(SAS),故本选项不合题意;
C、根据AB=AD,AC=AC,∠BCA=∠DCA不能推出△ABC≌△ADC,故本选项符合题意;
D、∵△ADC与△ABC的周长相等,AB=AD,AC=AC,
∴CB=CD,
由选项A可知△ABC≌△ADC,本选项不符合题意.
故选:C.
5.【解答】解:A、已知三边,且AB与BC两边之和AC,故能作出三角形,且能唯一画出△ABC;
B、∠A不是AB,BC的夹角,故不能唯一画出△ABC;
C、AB是∠A,∠B的夹边,故可唯一画出△ABC;
D、∠B是AB,BC的夹角,故不能唯一画出△ABC;
故选:B.
6.【解答】解:∵两个三角形全等,且∠A=∠D,BC对应FE,
按照规范的书写顺序:对应点写在对应位置上,
∴∠B=∠F,∠C=∠E,AB对应DF,△ABC≌△DFE,
故选:B.
7.【解答】解:①AB=DE,BC=EF,AC=DF,可根据SSS判定△ABC≌△DEF;
②AB=DE,∠B=∠E,BC=EF,可根据SAS判定△ABC≌△DEF;
③∠B=∠E,BC=EF,∠C=∠F,可根据ASA判定△ABC≌△DEF;
④∠A=∠D,∠B=∠E,∠C=∠F,不能判定△ABC≌△DEF;
故选:C.
8.【解答】解:∵∠B=70°,∠C=50°,
∴∠A=180°﹣70°﹣50°=60°,
根据“SAS”判断图乙中的三角形与△ABC全等;
根据“AAS”判断图丙中的三角形与△ABC全等;
根据“SSS”判断图丙中的三角形与△ABC全等.
根据“SSA”无法判断图甲中的三角形与△ABC全等.
故选:A.
9.【解答】解:A、添加条件∠A=∠D判定△ABC≌△DFE用的判定方法是ASA,故原题说法正确;
B、添加条件AB=DF不能判定△ABC≌△DFE,故原题说法错误;
C、添加条件BC=FE判定△ABC≌△DFE用的判定方法是SAS,故原题说法错误;
D、添加条件∠B=∠F判定△ABC≌△DFE用的判定方法是AAS,故原题说法错误;
故选:A.
10.【解答】证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS).
故选:D.
二.填空题
11.【解答】解:如右图所示,
∵以 A、B、P为顶点的三角形与△ABC全等,A(﹣2,1)、B(﹣2,﹣2)、C(4,﹣2),
∴点P的坐标为(4,1),(﹣8,1)或(﹣8,﹣2),
故答案为:(4,1),(﹣8,1)或(﹣8,﹣2).
12.【解答】解:∵AB=AD,AC=AC,
∴只要条件条件BC=DC,即可通过“SSS”判定△ABC≌△ADC,
故答案为:BC=DC,
13.【解答】解:OC=OD,
理由是:∵在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
故答案为:OC=OD或∠A=∠B或∠C=∠D.
14.【解答】证明:∵CB⊥AD,AE⊥CD,
∴∠ABF=∠CBD=∠AED=90°,
∴∠A+∠D=∠C+∠D=90°,
∴∠A=∠C,
在△ABF和△CBD中,,
∴△ABF≌△CBD(ASA),
∴BF=BD,
∵BC=AB=8,BF=BC﹣CF=8﹣2=6,
∴BD=BF=6;
故答案为:6.
15.【解答】解:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,
∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,
∴D1E1=C1D1sin30°=,
则B2C2=====()1,
同理可得:B3C3==()2,
∴正方形AnBn?nDn的边长是:()n﹣1,
则正方形A2020B2020C2020D2020的边长为:()2019,
故答案为:()2019.
三.解答题(共4小题)
16.【解答】证明:在△BME和△BND中,
,
∴△BME≌△BND(AAS),
∴BE=BD,
∵AM=CN,ME=DN,
∴AE=CD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS).
17.【解答】(1)证明:在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);
(2)解:由(1)可知,△ABC≌△DEF,
∴∠F=∠ACB,
∵∠A=60°,∠B=90°,
∴∠ACB=180°﹣(∠A+∠B)=180°﹣(60°+90°)=30°,
∴∠F=∠ACB=30°.
18.【解答】解:AB∥DE,
理由如下:
∵AF=DC,
∴AF+FC=DC+FC,
∴AC=DF( 等式性质),
∵BC∥EF,
∴∠BCA=∠EFD(两直线平行,内错角相等),
又∵BC=EF,
∴△ABC≌△DEF(SAS),
∴∠A=∠D(全等三角形的对应角相等),
∴AB∥DE(内错角相等,两直线平行),
故答案为:FC,等式的性质,EFD,SAS,D,DE.
19.【解答】解:(1)∵在△ABC中,AB=AC,
∴∠ABC=∠ACB,
故答案为:ACB;
(2)如图1,连接AN,并延长交DC的延长线于H,
∵∠BAM+∠MDC=180°,
∴AB∥CD,∠ADC=180°﹣∠BAM=110°,
∴∠BAN=∠CHN,
在△ABN和△HCN中,
,
∴△ABN≌△HCN(AAS),
∴AB=CH,AN=HN,
∵AB=AM,DC=DM,
∴AM+MD=CH+DC,
即AD=DH,
又∵AN=NH,
∴∠ADN=∠HDN==55°;
(3)如图2,延长DN至I使,NI=DN,连接AI,AD,
在△DNC和△INB中,
,
∴△DNC≌△INB(SAS),
∴DC=IB=MD,∠C=∠IBN,IN=DN,
∵∠BAM+∠MDC=180°,∠M+∠BAM+∠MDC+∠C+∠ABC=540°,
∴∠M+∠ABC+∠C=360°,
又∵∠ABC+∠IBN+∠ABI=360°,
∴∠M=∠ABI,
又∵AB=AM,MD=CD=BI,
∴△AMD≌△ABI(SAS),
∴AI=AD,
又∵NI=DN,
∴∠AND=∠ANI=90°
一.选择题
1.给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,AC=EF,∠B=∠E;
③∠B=∠E,AB=DF,∠C=∠F;
④AB=DE,AC=DF,∠B=∠E.
其中,能确定△ABC和△DEF全等的条件共有( )
A.1组 B.2组 C.3组 D.4组
2.下列各组条件中,不能判定△ABC≌△DEF全等的是( )
A.AC=DF,AB=DE,BC=EF B.∠A=∠D,AC=DF,AB=DE
C.∠B=∠E,∠C=∠F,BC=EF D.∠A=∠D,BC=DF,∠B=∠E
3.如图,∠ABD=∠EBC,BC=BD,再添加一个条件,使得△ABC≌△EBD,所添加的条件不正确的是( )
A.∠A=∠E B.BA=BE C.∠C=∠D D.AC=DE
4.已知,在△ABC与△ADC中,AB=AD,那么添加一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.△ADC与△ABC的周长相等
5.根据下列已知条件,不能唯一画出△ABC的是( )
A.AB=5,BC=3,AC=6 B.AB=4,BC=3,∠A=50°
C.∠A=50°,∠B=60°,AB=4 D.AB=10,BC=20,∠B=80°
6.如图,两个三角形全等,且∠A=∠D,BC对应FE.则( )
A.∠B=∠E B.∠C=∠E C.AB对应FD D.△ABC≌△DEF
7.在△ABC和△DEF中,给出下列四组条件:
①AB=DE,BC=EF,AC=DF;
②AB=DE,∠B=∠E,BC=EF;
③∠B=∠E,BC=EF,∠C=∠F;
④∠A=∠D,∠B=∠E,∠C=∠F;
其中,能使△ABC≌△DEF的条件共有( )
A.1组 B.2组 C.3组 D.4组
8.下列各图中a、b、c为△ABC的边长,根据图中标注数据,判断甲、乙、丙、丁四个三角形和如图△ABC不一定全等的是( )
A. B.
C. D.
9.已知:如图,AC=DE,∠1=∠2,要使△ABC≌△DFE,需添加一个条件,则添加的条件以及相应的判定定理合适的是( )
A.∠A=∠D(ASA) B.AB=DF(SAS) C.BC=FE(SSA) D.∠B=∠F(ASA)
10.如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A,B间的距离,但绳子不够长,一位同学帮他想了一个主意:先在地上取一个可以直接到达A,B的点C,连接AC并延长到点D,使CD=CA,连接BC并延长到点E,使CE=CB,连接DE并且测出DE的长即为A,B间的距离,这样实际上可以得到△ABC≌△DEC,理由是( )
A.SSS B.AAS C.ASA D.SAS
二.填空题
11.已知平面直角坐标系中A(﹣2,1)、B(﹣2,﹣2)、C(4,﹣2),以 A、B、P为顶点的三角形与△ABC全等,写出所有符合条件的点P的坐标 .(点P不与点C重合)
12.如图,AB=AD,只要再添加一个条件: ,就可以通过“SSS”判定△ABC≌△ADC.
13.如图,已知:AD与BC交于O点,OA=OB,要使△AOC≌△BOD,添加一个你认为合适的条件为 .
14.如图,已知CB⊥AD,AE⊥CD,垂足分别为B,E,AE,BC相交于点F,AB=BC.若AB=8,CF=2,则BD= .
15.在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3、…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2020B2020C2020D2020的边长是 .
三.解答题
16.已知:如图,点A、B、C在同一条直线上,AE与BD相交于M,CD与BE相交于点N,∠E=∠D,AM=CN,ME=ND.求证:△ABE≌△CBD.
17.如图,点A、D、C、F在同一条直线上,AC=DF,AB=DE,BC=EF.
(1)求证:△ABC≌△DEF;
(2)若∠A=60°,∠B=90°,求∠F的度数.
18.把下面的说理过程补充完整:
已知:如图,BC∥EF,BC=EF,AF=DC,线段AB和线段DE平行吗?请说明理由.
答:AB∥DE
理由:
∵AF=DC(已知)
∴AF+FC=DC+
∴AC=DF( )(填推理的依据)
∵BC∥EF(已知)
∴∠BCA=∠ (两直线平行,内错角相等)
又∵BC=EF(已知)
∴△ABC≌△DEF( )(填推理的依据)
∴∠A=∠ (全等三角形的对应角相等)
∴AB∥ (内错角相等,两直线平行)
19.已知∠BAM+∠MDC=180°,AB=AM,DC=DM,连接BC,N为BC的中点.
(1)①定理“等边对等角”即:对于任意△ABC若满足AB=AC,则∠ABC=∠ ;
②如图1若A、M、D共线,若∠BAM=70°,求∠NDC的大小;
(2)如图2,A、M、D不共线时,求∠ANB+∠DNC的值.
参考答案与试题解析
一.选择题
1.【解答】解:①AB=DE,BC=EF,AC=DF,可根据SSS判定△ABC≌△DEF;
②AB=DE,AC=EF,∠B=∠E,不能判定△ABC≌△DEF;
③∠B=∠E,AB=DF,∠C=∠F,不能判定△ABC≌△DEF;
④AB=DE,AC=DF,∠B=∠E,不能判定△ABC≌△DEF;
故选:A.
2.【解答】解:A、∵AC=DF,AB=DE,BC=EF,
∴利用SSS能推出△ABC≌△DEF,故本选项不符合题意;
B、∵∠A=∠D,AC=DF,AB=DE,
∴利用SAS能推出△ABC≌△DEF,故本选项不符合题意;
C、∵∠B=∠E,∠C=∠F,BC=EF,
∴利用ASA能推出△ABC≌△DEF,故本选项不符合题意;
D、∵∠A=∠D,BC=DF,∠B=∠E,BC和DF不是对应边,
∴不能推出△ABC≌△DEF,故本选项符合题意.
故选:D.
3.【解答】解:∵∠ABC=∠EBD,BC=BD,
∴当添加BA=BE时,可根据“SAS”判断△ABC≌△EBD;
当添加∠C=∠D时,可根据“ASA”判断△ABC≌△EBD;
当添加∠A=∠E时,可根据“AAS”判断△ABC≌△EBD.
故选:D.
4.【解答】解:A、∵在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),故本选项不合题意;
B、∵在△ABC和△ADC中,
,
∴△ABC≌△ADC(SAS),故本选项不合题意;
C、根据AB=AD,AC=AC,∠BCA=∠DCA不能推出△ABC≌△ADC,故本选项符合题意;
D、∵△ADC与△ABC的周长相等,AB=AD,AC=AC,
∴CB=CD,
由选项A可知△ABC≌△ADC,本选项不符合题意.
故选:C.
5.【解答】解:A、已知三边,且AB与BC两边之和AC,故能作出三角形,且能唯一画出△ABC;
B、∠A不是AB,BC的夹角,故不能唯一画出△ABC;
C、AB是∠A,∠B的夹边,故可唯一画出△ABC;
D、∠B是AB,BC的夹角,故不能唯一画出△ABC;
故选:B.
6.【解答】解:∵两个三角形全等,且∠A=∠D,BC对应FE,
按照规范的书写顺序:对应点写在对应位置上,
∴∠B=∠F,∠C=∠E,AB对应DF,△ABC≌△DFE,
故选:B.
7.【解答】解:①AB=DE,BC=EF,AC=DF,可根据SSS判定△ABC≌△DEF;
②AB=DE,∠B=∠E,BC=EF,可根据SAS判定△ABC≌△DEF;
③∠B=∠E,BC=EF,∠C=∠F,可根据ASA判定△ABC≌△DEF;
④∠A=∠D,∠B=∠E,∠C=∠F,不能判定△ABC≌△DEF;
故选:C.
8.【解答】解:∵∠B=70°,∠C=50°,
∴∠A=180°﹣70°﹣50°=60°,
根据“SAS”判断图乙中的三角形与△ABC全等;
根据“AAS”判断图丙中的三角形与△ABC全等;
根据“SSS”判断图丙中的三角形与△ABC全等.
根据“SSA”无法判断图甲中的三角形与△ABC全等.
故选:A.
9.【解答】解:A、添加条件∠A=∠D判定△ABC≌△DFE用的判定方法是ASA,故原题说法正确;
B、添加条件AB=DF不能判定△ABC≌△DFE,故原题说法错误;
C、添加条件BC=FE判定△ABC≌△DFE用的判定方法是SAS,故原题说法错误;
D、添加条件∠B=∠F判定△ABC≌△DFE用的判定方法是AAS,故原题说法错误;
故选:A.
10.【解答】证明:在△ABC和△DEC中,
∴△ABC≌△DEC(SAS).
故选:D.
二.填空题
11.【解答】解:如右图所示,
∵以 A、B、P为顶点的三角形与△ABC全等,A(﹣2,1)、B(﹣2,﹣2)、C(4,﹣2),
∴点P的坐标为(4,1),(﹣8,1)或(﹣8,﹣2),
故答案为:(4,1),(﹣8,1)或(﹣8,﹣2).
12.【解答】解:∵AB=AD,AC=AC,
∴只要条件条件BC=DC,即可通过“SSS”判定△ABC≌△ADC,
故答案为:BC=DC,
13.【解答】解:OC=OD,
理由是:∵在△AOC和△BOD中,
,
∴△AOC≌△BOD(SAS),
故答案为:OC=OD或∠A=∠B或∠C=∠D.
14.【解答】证明:∵CB⊥AD,AE⊥CD,
∴∠ABF=∠CBD=∠AED=90°,
∴∠A+∠D=∠C+∠D=90°,
∴∠A=∠C,
在△ABF和△CBD中,,
∴△ABF≌△CBD(ASA),
∴BF=BD,
∵BC=AB=8,BF=BC﹣CF=8﹣2=6,
∴BD=BF=6;
故答案为:6.
15.【解答】解:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,
∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,
∴D1E1=C1D1sin30°=,
则B2C2=====()1,
同理可得:B3C3==()2,
∴正方形AnBn?nDn的边长是:()n﹣1,
则正方形A2020B2020C2020D2020的边长为:()2019,
故答案为:()2019.
三.解答题(共4小题)
16.【解答】证明:在△BME和△BND中,
,
∴△BME≌△BND(AAS),
∴BE=BD,
∵AM=CN,ME=DN,
∴AE=CD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS).
17.【解答】(1)证明:在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);
(2)解:由(1)可知,△ABC≌△DEF,
∴∠F=∠ACB,
∵∠A=60°,∠B=90°,
∴∠ACB=180°﹣(∠A+∠B)=180°﹣(60°+90°)=30°,
∴∠F=∠ACB=30°.
18.【解答】解:AB∥DE,
理由如下:
∵AF=DC,
∴AF+FC=DC+FC,
∴AC=DF( 等式性质),
∵BC∥EF,
∴∠BCA=∠EFD(两直线平行,内错角相等),
又∵BC=EF,
∴△ABC≌△DEF(SAS),
∴∠A=∠D(全等三角形的对应角相等),
∴AB∥DE(内错角相等,两直线平行),
故答案为:FC,等式的性质,EFD,SAS,D,DE.
19.【解答】解:(1)∵在△ABC中,AB=AC,
∴∠ABC=∠ACB,
故答案为:ACB;
(2)如图1,连接AN,并延长交DC的延长线于H,
∵∠BAM+∠MDC=180°,
∴AB∥CD,∠ADC=180°﹣∠BAM=110°,
∴∠BAN=∠CHN,
在△ABN和△HCN中,
,
∴△ABN≌△HCN(AAS),
∴AB=CH,AN=HN,
∵AB=AM,DC=DM,
∴AM+MD=CH+DC,
即AD=DH,
又∵AN=NH,
∴∠ADN=∠HDN==55°;
(3)如图2,延长DN至I使,NI=DN,连接AI,AD,
在△DNC和△INB中,
,
∴△DNC≌△INB(SAS),
∴DC=IB=MD,∠C=∠IBN,IN=DN,
∵∠BAM+∠MDC=180°,∠M+∠BAM+∠MDC+∠C+∠ABC=540°,
∴∠M+∠ABC+∠C=360°,
又∵∠ABC+∠IBN+∠ABI=360°,
∴∠M=∠ABI,
又∵AB=AM,MD=CD=BI,
∴△AMD≌△ABI(SAS),
∴AI=AD,
又∵NI=DN,
∴∠AND=∠ANI=90°
