初中数学鲁教版八年级上册4.3中心对称练习题(Word版 含解析)
文档属性
| 名称 | 初中数学鲁教版八年级上册4.3中心对称练习题(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 259.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 00:00:00 | ||
图片预览




文档简介
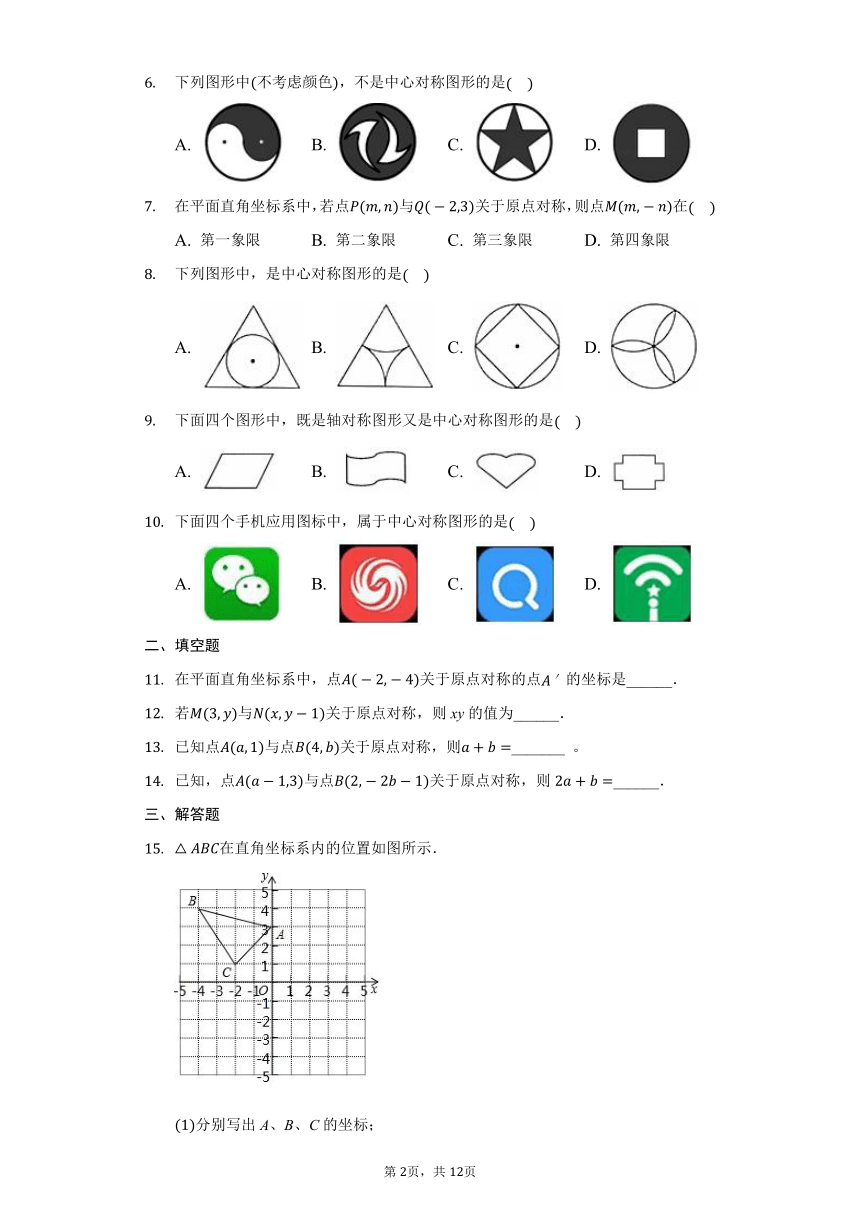
初中数学鲁教版八年级上册第四章3中心对称练习题
一、选择题
下列图形中,是中心对称图形的是
A.
B.
C.
D.
下列图形中,既是轴对称图形,又是中心对称图形的是
A.
B.
C.
D.
在天气预报图上,有各种各样表示天气的符号,下列表示天气符号的图形中,既是中心对称图形又是轴对称图形的是
A.
?晴
B.
冰雹
C.
?雷阵雨
D.
大雪
下列图形是我国国产品牌汽车的标识,这些汽车标识中,是中心对称图形的是
A.
B.
C.
D.
下列各图中,不是中心对称图形的为
A.
B.
C.
D.
下列图形中不考虑颜色,不是中心对称图形的是
A.
B.
C.
D.
在平面直角坐标系中,若点与关于原点对称,则点在
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
下列图形中,是中心对称图形的是
A.
B.
C.
D.
下面四个图形中,既是轴对称图形又是中心对称图形的是
A.
B.
C.
D.
下面四个手机应用图标中,属于中心对称图形的是
A.
B.
C.
D.
二、填空题
在平面直角坐标系中,点关于原点对称的点的坐标是______.
若与关于原点对称,则xy的值为______.
已知点与点关于原点对称,则_______
。
已知,点与点关于原点对称,则______.
三、解答题
在直角坐标系内的位置如图所示.
分别写出A、B、C的坐标;
请在这个坐标系内画出,使与关于y轴对称;
请在这个坐标系内画出,使与关于原点对称,并写出的坐标.
已知点与点关于x轴对称,点与点D关于原点对称.
求点A、B、C、D的坐标;
顺次联结点A、D、B、C,求所得图形的面积.
如图,线段CD是线段AB经过某种变换得到的图形.
若点A与点C,点B与点D是对应点,第一象限内的点M的坐标为,在这种变换下,点M的对应点N的坐标为______用含m、n的式子表示;
若点A与点D、点B与点C是对应点,第一象限内的点M的坐标为,在这种变换下,点M的对应点N的坐标为______用含m、n的式子表示;
连接BD、AC,直接写出四边形ABDC的面积为______.
如图,中,,D、E分别是边BC、AC的中点.将绕点E旋转180度,得.
判断四边形ABDF的形状,并证明;
已知,,求四边形ABDF的面积S.
答案和解析
1.【答案】D
【解析】解:A、不是中心对称图形,故本选项错误;
B、不是中心对称图形,故本选项错误;
C、不是中心对称图形,故本选项错误;
D、是中心对称图形,故本选项正确.
故选:D.
根据中心对称图形的概念对各选项分析判断即可得解.
本题考查了中心对称图形的概念.中心对称图形是要寻找对称中心,旋转180度后两部分重合.
2.【答案】A
【解析】解:A、是中心对称图形,也是轴对称图形,符合题意;
B、不是中心对称图形,是轴对称图形,不符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、不是轴对称图形,也不是中心对称图形,不符合题意.
故选:A.
根据轴对称图形、中心对称图形的定义即可判断.
此题主要考查了中心对称图形与轴对称图形的概念,正确掌握相关定义是解题关键.
3.【答案】A
【解析】
【分析】
此题主要考查了好中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.根据轴对称图形与中心对称图形的概念求解.
【解答】
解:A、是轴对称图形,也是中心对称图形,故此选项正确;
B、是轴对称图形,不是中心对称图形,故此选项错误;
C、不是轴对称图形,是中心对称图形,故此选项错误;
D、是轴对称图形,不是中心对称图形,故此选项错误.
故选:A.
4.【答案】D
【解析】解:A、不是中心对称图形,故此选项错误;
B、不是中心对称图形,故此选项错误;
C、不是中心对称图形,故此选项错误;
D、是中心对称图形,故此选项正确;
故选:D.
根据把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心进行分析.
此题主要考查了中心对称图形,关键是掌握中心对称图形的定义.
5.【答案】A
【解析】解:正五边形是轴对称图形,不是中心对称图形,故本选项符合题意;
B.矩形既是轴对称图形又是中心对称图形,故本选项不合题意;
C.平行四边形不是轴对称图形,是中心对称图形形,故本选项不合题意;
D.圆既是轴对称图形又是中心对称图形,故本选项不合题意;
故选:A.
根据轴对称图形与中心对称图形的概念求解.
此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
6.【答案】C
【解析】解:A、是中心对称图形,故此选项不合题意;
B、是中心对称图形,故此选项不合题意;
C、不是中心对称图形,是轴对称图形,故此选项符合题意;
D、是中心对称图形,故此选项不合题意;
故选:C.
直接利用中心对称图形的定义得出答案.
此题主要考查了中心对称图形,正确把握定义是解题关键.
7.【答案】A
【解析】解:点与点关于原点对称,
,则点坐标为:.
故选:A.
根据关于原点对称的点的坐标特点:两个点关于原点对称时,它们的坐标符号相反,即点关于原点O的对称点是确定m、n的值,即可得出答案.
本题考查了平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,该题比较简单.
8.【答案】C
【解析】解:A、不是中心对称图形,故本选项不符合题意;
B、不是中心对称图形,故本选项不符合题意;
C、是中心对称图形,故本选项符合题意;
D、不是中心对称图形,故本选项不符合题意.
故选:C.
根据中心对称图形的定义逐个判断即可.
本题考查了对中心对称图形的定义,能熟知中心对称图形的定义是解此题的关键.
9.【答案】D
【解析】解:A、不是轴对称图形,是中心对称图形,故此选项错误;
B、不是轴对称图形,不是中心对称图形,故此选项错误;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、是轴对称图形,也是中心对称图形,故此选项正确.
故选:D.
根据轴对称图形与中心对称图形的概念求解.
此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
10.【答案】B
【解析】解:A、图形不是中心对称图形;
B、图形是中心对称图形;
C、图形不是中心对称图形;
D、图形不是中心对称图形,
故选:B.
根据中心对称图形的概念进行判断即可.
本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后能与自身重合.
11.【答案】
【解析】解:点关于原点对称的点的坐标是.
故答案为:.
直接利用关于原点对称点的性质得出答案.
此题主要考查了关于原点对称点的性质,正确掌握对称点坐标特点是解题关键.
12.【答案】
【解析】解:与关于原点对称,
,,
解得:,,
,
故答案为:.
根据关于原点对称点的性质可得,,解出y的值,然后可得答案.
此题主要考查了关于原点对称的点的坐标,关键是掌握两个点关于原点对称时,它们的坐标符号相反.
13.【答案】
【解析】解:点与点关于原点对称,
、b的值分别为,.
所以,
故答案为:
根据“两点关于原点对称,则两点的横、纵坐标都是互为相反数”解答.
本题考查了关于原点对称的点的坐标:两点关于原点对称,则两点的横、纵坐标都是互为相反数.
14.【答案】
【解析】解:点与点关于原点对称,
,,
解得:,,
,
故答案为:.
根据关于原点对称点的坐标特点可得,,解出a、b的值,然后可得答案.
此题主要考查了关于原点对称点的坐标,关键是掌握两个点关于原点对称时,它们的坐标符号相反.
15.【答案】解:;;;
如图:
?
如图:.
【解析】本题考查了轴对称变换与关于原点对称的图形的性质.
观察平面直角坐标系,根据点与坐标系的关系,即可求得A、B、C的坐标;
根据关于y轴对称的图形的特点,首先求得各对称点的坐标,继而画出;
根据关于原点对称的图形的特点,首先求得各对称点的坐标,继而画出,写出坐标;
16.【答案】解:点与点关于x轴对称,
,,
解得,,
点,,,
点与点D关于原点对称,
点;
如图所示:
四边形ADBC的面积为:.
【解析】本题考查的是作图轴对称变换,熟知关于x、y轴对称的点的坐标特点是解答此题的关键.
根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,分别求出a,b的值,进而求出点A、B、C的坐标,再根据关于原点的对称点,横纵坐标都变成相反数求出点D的坐标;
把这些点按顺次连接起来,再根据三角形的面积公式计算其面积即可.
17.【答案】?
?
10
【解析】解:点A向左平移5个单位长度,再向下平移5个单位长度点C,
点M的对应点N的坐标为;
点A与点D关于原点对称,
点M的对应点N的坐标为;
如图所示:
四边形ABDC的面积;
故答案为:;;
根据对应点的坐标利用平移的性质解答;
根据中心对称的性质写出坐标即可;
根据四边形的面积公式解答即可.
本题考查了利用平移变换作图,关键是根据中心对称的性质,三角形的面积求解.
18.【答案】解:结论:四边形ABDF是菱形.
,,
,,
由旋转的性质可知,,
,,
四边形ABDF是平行四边形,
,,
,
四边形ABDF是菱形.
连接BF,AD交于点O.
四边形ABDF是菱形,
,,,设,,
则有,
,
,
,
.
【解析】结论:四边形ABDF是菱形.根据邻边相等的平行四边形是菱形证明即可.
设,,构建方程组求出2xy即可解决问题.
本题考查中心对称,三角形的面积,三角形的中位线定理,菱形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
第2页,共2页
第1页,共1页
一、选择题
下列图形中,是中心对称图形的是
A.
B.
C.
D.
下列图形中,既是轴对称图形,又是中心对称图形的是
A.
B.
C.
D.
在天气预报图上,有各种各样表示天气的符号,下列表示天气符号的图形中,既是中心对称图形又是轴对称图形的是
A.
?晴
B.
冰雹
C.
?雷阵雨
D.
大雪
下列图形是我国国产品牌汽车的标识,这些汽车标识中,是中心对称图形的是
A.
B.
C.
D.
下列各图中,不是中心对称图形的为
A.
B.
C.
D.
下列图形中不考虑颜色,不是中心对称图形的是
A.
B.
C.
D.
在平面直角坐标系中,若点与关于原点对称,则点在
A.
第一象限
B.
第二象限
C.
第三象限
D.
第四象限
下列图形中,是中心对称图形的是
A.
B.
C.
D.
下面四个图形中,既是轴对称图形又是中心对称图形的是
A.
B.
C.
D.
下面四个手机应用图标中,属于中心对称图形的是
A.
B.
C.
D.
二、填空题
在平面直角坐标系中,点关于原点对称的点的坐标是______.
若与关于原点对称,则xy的值为______.
已知点与点关于原点对称,则_______
。
已知,点与点关于原点对称,则______.
三、解答题
在直角坐标系内的位置如图所示.
分别写出A、B、C的坐标;
请在这个坐标系内画出,使与关于y轴对称;
请在这个坐标系内画出,使与关于原点对称,并写出的坐标.
已知点与点关于x轴对称,点与点D关于原点对称.
求点A、B、C、D的坐标;
顺次联结点A、D、B、C,求所得图形的面积.
如图,线段CD是线段AB经过某种变换得到的图形.
若点A与点C,点B与点D是对应点,第一象限内的点M的坐标为,在这种变换下,点M的对应点N的坐标为______用含m、n的式子表示;
若点A与点D、点B与点C是对应点,第一象限内的点M的坐标为,在这种变换下,点M的对应点N的坐标为______用含m、n的式子表示;
连接BD、AC,直接写出四边形ABDC的面积为______.
如图,中,,D、E分别是边BC、AC的中点.将绕点E旋转180度,得.
判断四边形ABDF的形状,并证明;
已知,,求四边形ABDF的面积S.
答案和解析
1.【答案】D
【解析】解:A、不是中心对称图形,故本选项错误;
B、不是中心对称图形,故本选项错误;
C、不是中心对称图形,故本选项错误;
D、是中心对称图形,故本选项正确.
故选:D.
根据中心对称图形的概念对各选项分析判断即可得解.
本题考查了中心对称图形的概念.中心对称图形是要寻找对称中心,旋转180度后两部分重合.
2.【答案】A
【解析】解:A、是中心对称图形,也是轴对称图形,符合题意;
B、不是中心对称图形,是轴对称图形,不符合题意;
C、不是轴对称图形,是中心对称图形,不符合题意;
D、不是轴对称图形,也不是中心对称图形,不符合题意.
故选:A.
根据轴对称图形、中心对称图形的定义即可判断.
此题主要考查了中心对称图形与轴对称图形的概念,正确掌握相关定义是解题关键.
3.【答案】A
【解析】
【分析】
此题主要考查了好中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.根据轴对称图形与中心对称图形的概念求解.
【解答】
解:A、是轴对称图形,也是中心对称图形,故此选项正确;
B、是轴对称图形,不是中心对称图形,故此选项错误;
C、不是轴对称图形,是中心对称图形,故此选项错误;
D、是轴对称图形,不是中心对称图形,故此选项错误.
故选:A.
4.【答案】D
【解析】解:A、不是中心对称图形,故此选项错误;
B、不是中心对称图形,故此选项错误;
C、不是中心对称图形,故此选项错误;
D、是中心对称图形,故此选项正确;
故选:D.
根据把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心进行分析.
此题主要考查了中心对称图形,关键是掌握中心对称图形的定义.
5.【答案】A
【解析】解:正五边形是轴对称图形,不是中心对称图形,故本选项符合题意;
B.矩形既是轴对称图形又是中心对称图形,故本选项不合题意;
C.平行四边形不是轴对称图形,是中心对称图形形,故本选项不合题意;
D.圆既是轴对称图形又是中心对称图形,故本选项不合题意;
故选:A.
根据轴对称图形与中心对称图形的概念求解.
此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
6.【答案】C
【解析】解:A、是中心对称图形,故此选项不合题意;
B、是中心对称图形,故此选项不合题意;
C、不是中心对称图形,是轴对称图形,故此选项符合题意;
D、是中心对称图形,故此选项不合题意;
故选:C.
直接利用中心对称图形的定义得出答案.
此题主要考查了中心对称图形,正确把握定义是解题关键.
7.【答案】A
【解析】解:点与点关于原点对称,
,则点坐标为:.
故选:A.
根据关于原点对称的点的坐标特点:两个点关于原点对称时,它们的坐标符号相反,即点关于原点O的对称点是确定m、n的值,即可得出答案.
本题考查了平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,该题比较简单.
8.【答案】C
【解析】解:A、不是中心对称图形,故本选项不符合题意;
B、不是中心对称图形,故本选项不符合题意;
C、是中心对称图形,故本选项符合题意;
D、不是中心对称图形,故本选项不符合题意.
故选:C.
根据中心对称图形的定义逐个判断即可.
本题考查了对中心对称图形的定义,能熟知中心对称图形的定义是解此题的关键.
9.【答案】D
【解析】解:A、不是轴对称图形,是中心对称图形,故此选项错误;
B、不是轴对称图形,不是中心对称图形,故此选项错误;
C、是轴对称图形,不是中心对称图形,故此选项错误;
D、是轴对称图形,也是中心对称图形,故此选项正确.
故选:D.
根据轴对称图形与中心对称图形的概念求解.
此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.
10.【答案】B
【解析】解:A、图形不是中心对称图形;
B、图形是中心对称图形;
C、图形不是中心对称图形;
D、图形不是中心对称图形,
故选:B.
根据中心对称图形的概念进行判断即可.
本题考查的是中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后能与自身重合.
11.【答案】
【解析】解:点关于原点对称的点的坐标是.
故答案为:.
直接利用关于原点对称点的性质得出答案.
此题主要考查了关于原点对称点的性质,正确掌握对称点坐标特点是解题关键.
12.【答案】
【解析】解:与关于原点对称,
,,
解得:,,
,
故答案为:.
根据关于原点对称点的性质可得,,解出y的值,然后可得答案.
此题主要考查了关于原点对称的点的坐标,关键是掌握两个点关于原点对称时,它们的坐标符号相反.
13.【答案】
【解析】解:点与点关于原点对称,
、b的值分别为,.
所以,
故答案为:
根据“两点关于原点对称,则两点的横、纵坐标都是互为相反数”解答.
本题考查了关于原点对称的点的坐标:两点关于原点对称,则两点的横、纵坐标都是互为相反数.
14.【答案】
【解析】解:点与点关于原点对称,
,,
解得:,,
,
故答案为:.
根据关于原点对称点的坐标特点可得,,解出a、b的值,然后可得答案.
此题主要考查了关于原点对称点的坐标,关键是掌握两个点关于原点对称时,它们的坐标符号相反.
15.【答案】解:;;;
如图:
?
如图:.
【解析】本题考查了轴对称变换与关于原点对称的图形的性质.
观察平面直角坐标系,根据点与坐标系的关系,即可求得A、B、C的坐标;
根据关于y轴对称的图形的特点,首先求得各对称点的坐标,继而画出;
根据关于原点对称的图形的特点,首先求得各对称点的坐标,继而画出,写出坐标;
16.【答案】解:点与点关于x轴对称,
,,
解得,,
点,,,
点与点D关于原点对称,
点;
如图所示:
四边形ADBC的面积为:.
【解析】本题考查的是作图轴对称变换,熟知关于x、y轴对称的点的坐标特点是解答此题的关键.
根据关于x轴对称的点的坐标规律:横坐标相同,纵坐标互为相反数,分别求出a,b的值,进而求出点A、B、C的坐标,再根据关于原点的对称点,横纵坐标都变成相反数求出点D的坐标;
把这些点按顺次连接起来,再根据三角形的面积公式计算其面积即可.
17.【答案】?
?
10
【解析】解:点A向左平移5个单位长度,再向下平移5个单位长度点C,
点M的对应点N的坐标为;
点A与点D关于原点对称,
点M的对应点N的坐标为;
如图所示:
四边形ABDC的面积;
故答案为:;;
根据对应点的坐标利用平移的性质解答;
根据中心对称的性质写出坐标即可;
根据四边形的面积公式解答即可.
本题考查了利用平移变换作图,关键是根据中心对称的性质,三角形的面积求解.
18.【答案】解:结论:四边形ABDF是菱形.
,,
,,
由旋转的性质可知,,
,,
四边形ABDF是平行四边形,
,,
,
四边形ABDF是菱形.
连接BF,AD交于点O.
四边形ABDF是菱形,
,,,设,,
则有,
,
,
,
.
【解析】结论:四边形ABDF是菱形.根据邻边相等的平行四边形是菱形证明即可.
设,,构建方程组求出2xy即可解决问题.
本题考查中心对称,三角形的面积,三角形的中位线定理,菱形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
第2页,共2页
第1页,共1页
