23.2 解直角三角形及其应用 第1课时 解直角三角形 课件(共21张PPT)
文档属性
| 名称 | 23.2 解直角三角形及其应用 第1课时 解直角三角形 课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 16:31:44 | ||
图片预览




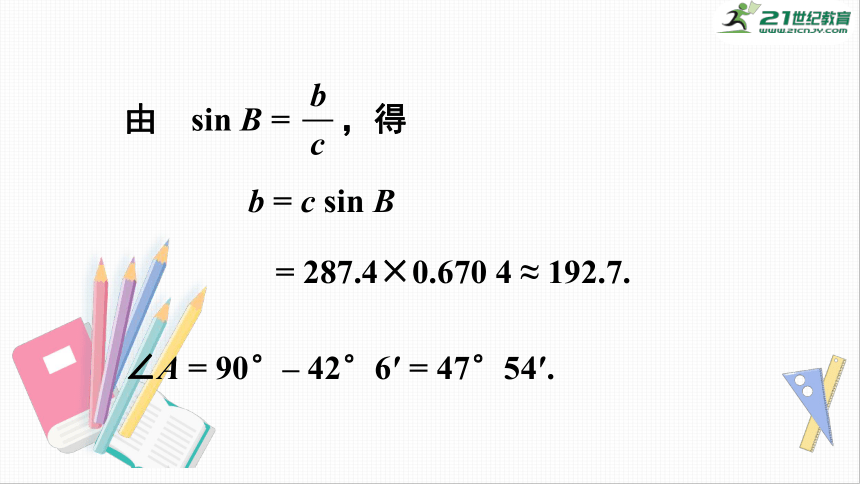

文档简介
(共21张PPT)
第1课时
解直角三角形
23.2
解直角三角形及其应用
沪科版
九年级数学上册
教学课件
学习目标
【知识与技能】
使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.
【过程与方法】
通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.
【情感态度】
渗透数形结合的数学思想,培养学生良好的学习习惯.
【教学重点】
直角三角形的解法.
【教学难点】
三角函数在解直角三角形中的灵活运用.
新课导入
A
C
B
a
b
c
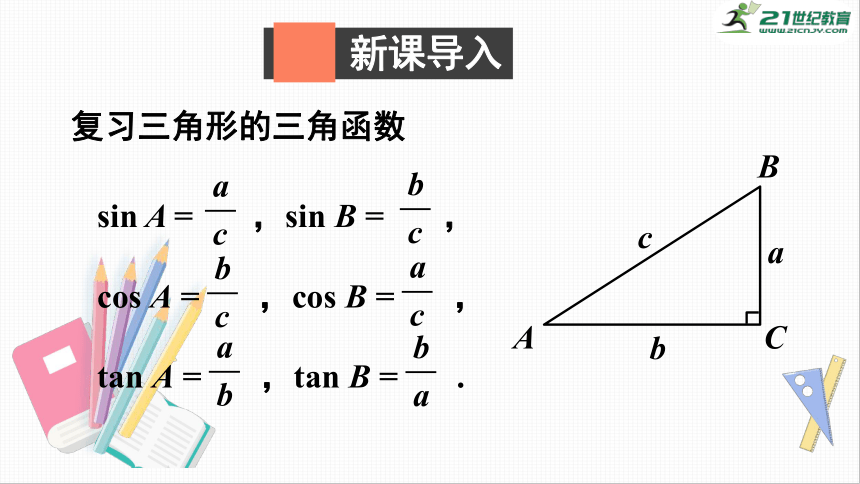
复习三角形的三角函数
sin
A
=
,sin
B
=
,
cos
A
=
,cos
B
=
,
tan
A
=
,tan
B
=
.
a
c
a
b
b
c
b
a
b
c
a
c
新课探究
观察
A
C
B
a
b
c
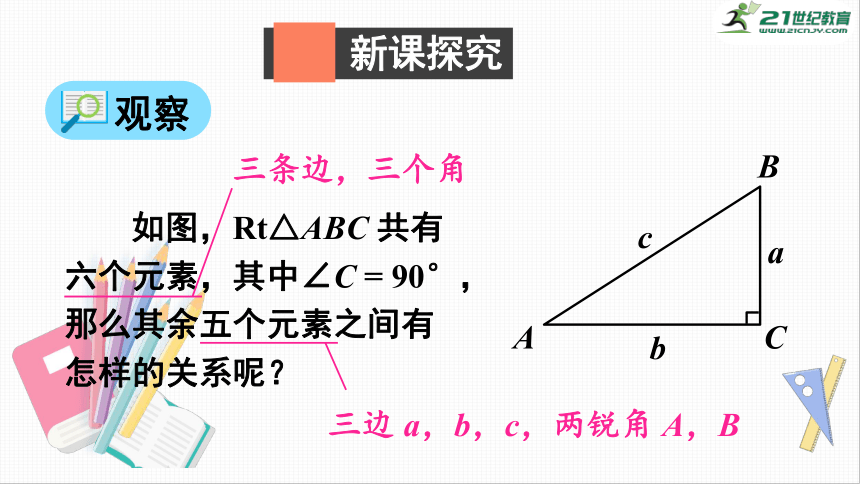
如图,Rt△ABC
共有六个元素,其中∠C
=
90°,那么其余五个元素之间有怎样的关系呢?
三条边,三个角
三边
a,b,c,两锐角
A,B
A
C
B
a
b
c
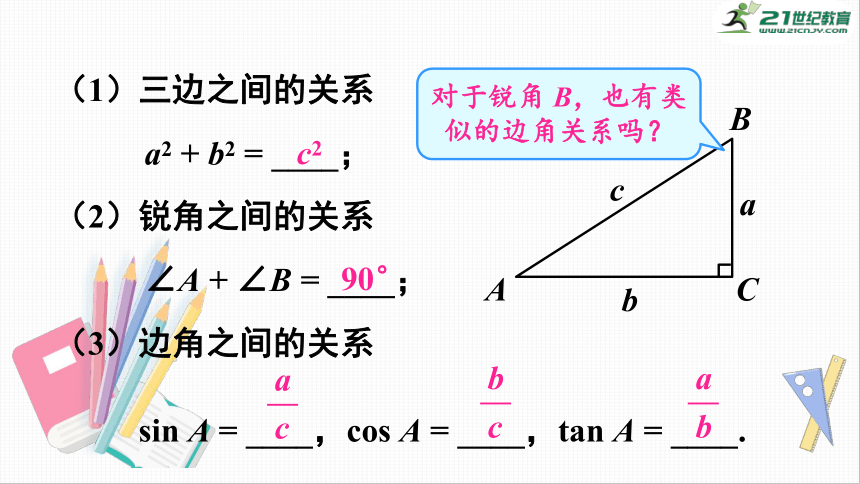
(1)三边之间的关系
a2
+
b2
=
____;
(2)锐角之间的关系
∠A
+
∠B
=
____;
(3)边角之间的关系
sin
A
=
____,cos
A
=
____,tan
A
=
____.
c2
90°
a
c
b
c
a
b
对于锐角
B,也有类似的边角关系吗?
有了以上关系,如果知道了五个元素中的两个元素(至少有一个元素是边),就可以求出其余的三个元素.
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形.
例
1
在
Rt△ABC
中,∠C
=
90°,∠B
=
42°6′,c
=
287.4,解这个直角三角形(精确到
0.1).
解
由
cos
B
=
,得
a
c
a
=
c
cos
B
=
287.4×0.742
0
≈
213.3.
由
sin
B
=
,得
b
c
b
=
c
sin
B
=
287.4×0.670
4
≈
192.7.
∠A
=
90°–
42°6′
=
47°54′.
练习
根据下列条件,解直角三角形.
在
Rt△ABC
中,∠C
=
90°,a
=
30,∠B
=
80°.
解
由
cos
B
=
,得
a
c
c
=
=
≈
172.8
a
cos
B
30
0.173
6
由
tan
B
=
,得
b
a
b
=
a
tan
B
=
30×5.671
3
≈
170.1
例
2
在Rt△
ABC
中,∠A
=
55°,b
=
20
cm,c
=
30
cm,求三角形的面积
S△ABC(精确到
0.1
cm2).
A
B
C
55°
c
b
解
如图,作
AB
上的高
CD,
在Rt△ACD
中,
∵
CD
=
AC
·
sin
A
=
b
sin
A,
∴
S△ABC
=
AB
·
CD
=
bc
sin
A.
D
A
B
C
55°
c
b
当∠A
=
55°,b
=
20
cm,c
=
30
cm
时,有
S△ABC
=
bc
sin
A
=
×20×30
sin
55°
=
×20×30
×0.819
2
≈
245.8(cm2)
练习
在四边形
ABCD
中,AB∥CD,AB
=
4,CD
=
8,AD
=
6,∠D
=
43°,求四边形的面积(精确到0.01).
B
A
C
D
E
解
如图,作
CD
上的高
AE,
43°
∴AE
=
AD
·
sin
43°=
6
sin
43°
B
A
C
D
E
43°
S四边形ABCD
=
(AB
+
CD)×AE
=
(4
+
8)×6
sin
43°
=
×12×6×0.682
0
≈
24.6
随堂演练
1.
在
Rt△ABC
中,∠C
=
90°,BC
=
,AC
=
,则∠A
=
(
).
A.
90°
B.
60°
C.
45°
D.
30°
D
2.
在△ABC
中,∠C
为直角,∠A、∠B、∠C
所对的边分别为
a,b,c,且
a
=
,b
=
3,解这个三角形.
解
c
=
=
tan
B
=
=
=
b
a
∴
∠B
=
60°
∠A
=
90°–
60°=
30°.
3.
如图,在△ABC
中,∠A
=
60°,AB
=
6,AC
=
5
,求
S△ABC
.
A
B
C
60°
6
5
解
如图,作
AB
上的高
CD,
在Rt△ACD
中,
CD
=
AC
·
sin
A
,
∴
S△ABC
=
AB
·
CD
=
×5×6
sin
A
≈
13.0
.
D
4.
在
Rt△ABC
中,∠C
=
90°,∠B
=
30°,AD
是
△ABC
的角平分线,若
AC
=
,求线段AD
的长.
A
C
B
D
30°
解
∵∠B
=
30°,∴∠BAC
=
90°–
30°=
60°,因为
AD
是∠BAC
的角平分线,
∴∠DAC
=
30°.
由
cos
∠DAC
=
,得
AD
=
=
2.
课堂小结
在直角三角形中,如果知道了五个元素中的两个元素(至少有一个元素是边),就可以求出其余的三个元素.
这就是解直角三角形.
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第1课时
解直角三角形
23.2
解直角三角形及其应用
沪科版
九年级数学上册
教学课件
学习目标
【知识与技能】
使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形.
【过程与方法】
通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.
【情感态度】
渗透数形结合的数学思想,培养学生良好的学习习惯.
【教学重点】
直角三角形的解法.
【教学难点】
三角函数在解直角三角形中的灵活运用.
新课导入
A
C
B
a
b
c
复习三角形的三角函数
sin
A
=
,sin
B
=
,
cos
A
=
,cos
B
=
,
tan
A
=
,tan
B
=
.
a
c
a
b
b
c
b
a
b
c
a
c
新课探究
观察
A
C
B
a
b
c
如图,Rt△ABC
共有六个元素,其中∠C
=
90°,那么其余五个元素之间有怎样的关系呢?
三条边,三个角
三边
a,b,c,两锐角
A,B
A
C
B
a
b
c
(1)三边之间的关系
a2
+
b2
=
____;
(2)锐角之间的关系
∠A
+
∠B
=
____;
(3)边角之间的关系
sin
A
=
____,cos
A
=
____,tan
A
=
____.
c2
90°
a
c
b
c
a
b
对于锐角
B,也有类似的边角关系吗?
有了以上关系,如果知道了五个元素中的两个元素(至少有一个元素是边),就可以求出其余的三个元素.
在直角三角形中,除直角外,由已知元素求出未知元素的过程,叫做解直角三角形.
例
1
在
Rt△ABC
中,∠C
=
90°,∠B
=
42°6′,c
=
287.4,解这个直角三角形(精确到
0.1).
解
由
cos
B
=
,得
a
c
a
=
c
cos
B
=
287.4×0.742
0
≈
213.3.
由
sin
B
=
,得
b
c
b
=
c
sin
B
=
287.4×0.670
4
≈
192.7.
∠A
=
90°–
42°6′
=
47°54′.
练习
根据下列条件,解直角三角形.
在
Rt△ABC
中,∠C
=
90°,a
=
30,∠B
=
80°.
解
由
cos
B
=
,得
a
c
c
=
=
≈
172.8
a
cos
B
30
0.173
6
由
tan
B
=
,得
b
a
b
=
a
tan
B
=
30×5.671
3
≈
170.1
例
2
在Rt△
ABC
中,∠A
=
55°,b
=
20
cm,c
=
30
cm,求三角形的面积
S△ABC(精确到
0.1
cm2).
A
B
C
55°
c
b
解
如图,作
AB
上的高
CD,
在Rt△ACD
中,
∵
CD
=
AC
·
sin
A
=
b
sin
A,
∴
S△ABC
=
AB
·
CD
=
bc
sin
A.
D
A
B
C
55°
c
b
当∠A
=
55°,b
=
20
cm,c
=
30
cm
时,有
S△ABC
=
bc
sin
A
=
×20×30
sin
55°
=
×20×30
×0.819
2
≈
245.8(cm2)
练习
在四边形
ABCD
中,AB∥CD,AB
=
4,CD
=
8,AD
=
6,∠D
=
43°,求四边形的面积(精确到0.01).
B
A
C
D
E
解
如图,作
CD
上的高
AE,
43°
∴AE
=
AD
·
sin
43°=
6
sin
43°
B
A
C
D
E
43°
S四边形ABCD
=
(AB
+
CD)×AE
=
(4
+
8)×6
sin
43°
=
×12×6×0.682
0
≈
24.6
随堂演练
1.
在
Rt△ABC
中,∠C
=
90°,BC
=
,AC
=
,则∠A
=
(
).
A.
90°
B.
60°
C.
45°
D.
30°
D
2.
在△ABC
中,∠C
为直角,∠A、∠B、∠C
所对的边分别为
a,b,c,且
a
=
,b
=
3,解这个三角形.
解
c
=
=
tan
B
=
=
=
b
a
∴
∠B
=
60°
∠A
=
90°–
60°=
30°.
3.
如图,在△ABC
中,∠A
=
60°,AB
=
6,AC
=
5
,求
S△ABC
.
A
B
C
60°
6
5
解
如图,作
AB
上的高
CD,
在Rt△ACD
中,
CD
=
AC
·
sin
A
,
∴
S△ABC
=
AB
·
CD
=
×5×6
sin
A
≈
13.0
.
D
4.
在
Rt△ABC
中,∠C
=
90°,∠B
=
30°,AD
是
△ABC
的角平分线,若
AC
=
,求线段AD
的长.
A
C
B
D
30°
解
∵∠B
=
30°,∴∠BAC
=
90°–
30°=
60°,因为
AD
是∠BAC
的角平分线,
∴∠DAC
=
30°.
由
cos
∠DAC
=
,得
AD
=
=
2.
课堂小结
在直角三角形中,如果知道了五个元素中的两个元素(至少有一个元素是边),就可以求出其余的三个元素.
这就是解直角三角形.
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
