23.2 解直角三角形及其应用 第2课时 解决单一直角三角形问题 课件(共18张PPT)
文档属性
| 名称 | 23.2 解直角三角形及其应用 第2课时 解决单一直角三角形问题 课件(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 16:30:51 | ||
图片预览




文档简介
(共18张PPT)
第2课时
解决单一直角三角形问题
23.2
解直角三角形及其应用
沪科版
九年级数学上册
教学课件
学习目标
【知识与技能】
比较熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
【过程与方法】
通过学习进一步掌握解直角三角形的方法.
【情感态度】
培养学生把实际问题转化为数学问题的能力.
【教学重点】
应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
【教学难点】
选用恰当的直角三角形,解题思路分析.
新课导入
A
C
B
a
b
c
直角三角形的边角数量关系有哪些?
a2
+
b2
=
c2
∠A
+
∠B
=
90°
sin
A
=
,sin
B
=
,
cos
A
=
,cos
B
=
,
tan
A
=
,tan
B
=
.
a
c
a
b
b
c
b
a
b
c
a
c
新课探究
解直角三角形在实际问题中有着广泛的应用.
例
3
如图,一学生要测量校园内一棵水杉树的高度.
他站在距离水杉树
8
m
的
E
处,测得树顶的仰角∠ACD
=
52°,已知测角器的架高
CE
=
1.6
m,问树高
AB
为多少米?(精确到0.1m)
E
B
D
C
A
52°
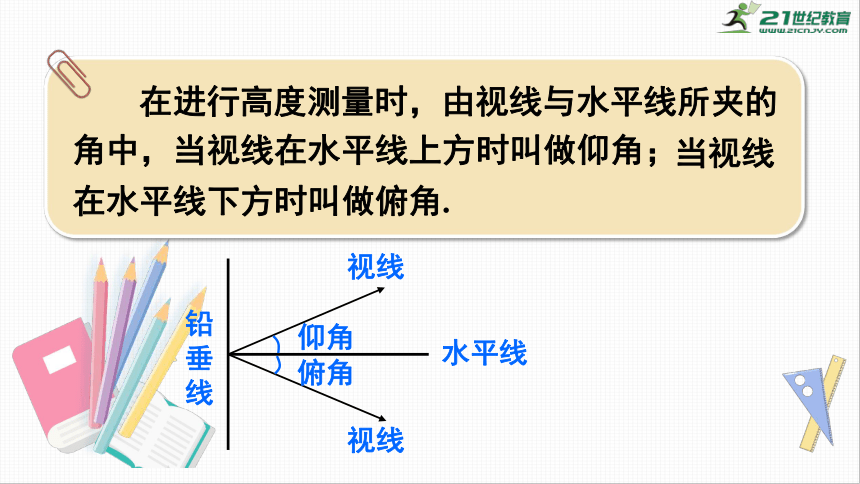
在进行高度测量时,由视线与水平线所夹的角中,当视线在水平线上方时叫做仰角;
当视线在水平线下方时叫做俯角.
铅垂线
水平线
仰角
俯角
视线
视线
E
B
D
C
A
52°
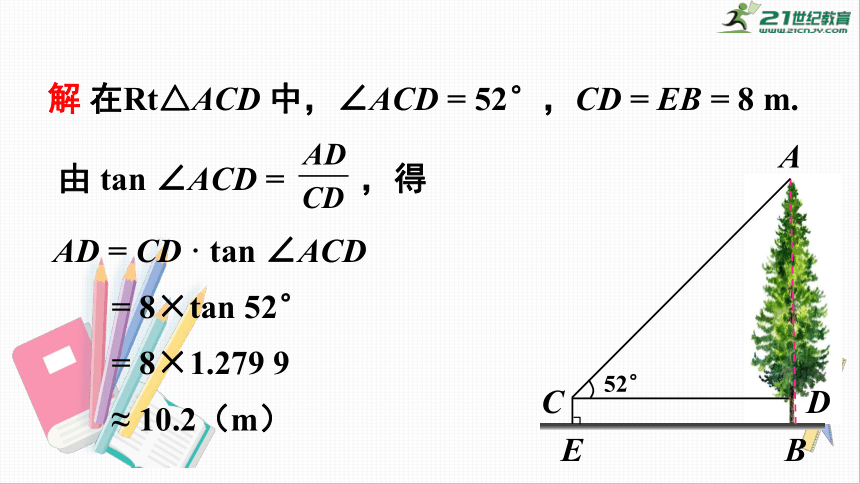
解
在Rt△ACD
中,∠ACD
=
52°,CD
=
EB
=
8
m.
由
tan
∠ACD
=
,得
AD
=
CD
·
tan
∠ACD
=
8×tan
52°
=
8×1.279
9
≈
10.2(m)
E
B
D
C
A
52°
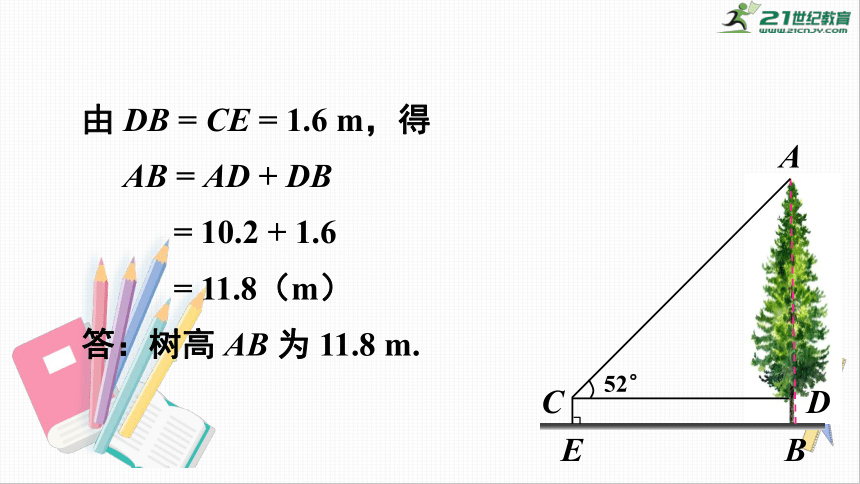
由
DB
=
CE
=
1.6
m,得
AB
=
AD
+
DB
=
10.2
+
1.6
=
11.8(m)
答:树高
AB
为
11.8
m.
练习
如图,飞机的飞行高度
AB
=
1
000
m.
从飞机上测得到地面着陆点
C
的俯角为18°,求飞机到着陆点的距离
AC
的值(精确到
1
m).
A
B
C
18°
解
由题意得∠C
=
18°,
sin
C
=
∴AC
=
A
B
C
18°
=
≈
3236(m)
随堂演练
1.
如图,在电线杆上离地面
6
米处用拉线固定电线杆,拉线和地面之间的夹角为
60°
,求拉线AC
的长和拉线下端点
A
与线杆底部
D
的距离(精确到
0.1
米).
6
米
A
D
C
60°
B
6
米
A
D
C
B
60°
解
由
sin
A
=
,得
AC
=
=
≈
6.9(米)
由
tan
A
=
,得
AD
=
=
≈
3.5(米)
2.
如图,沿
AC
方向开山修路,为了加快施工进度,要在小山另一侧的
E
处同时施工.
如果从
AC
上取一点
B,使∠ABD
=
140°,
BD
=
520
m,∠D
=
50°,那么开挖点
E
离
点D
多远,才能使点
A,C,E
正好在一条直线上?(精确到1
m)
140°
50°
A
B
E
D
C
140°
50°
A
B
E
D
C
解
连接
CE.
∵∠ABD
=
140°,
∴∠DBE
=
180°–
140°=
40°.
∴∠E
=
180°–
40°–
50°=
90°
由
cos
D
=
,得
DE
=
BD
·
cos
D
=
520×cos
50°≈
334(m)
3.
如图,一架梯子斜靠在墙上,梯子顶端到地面的距离
BC
=
3.2
米,底端到墙根的距离
AC
=
2.4
米.
(1)求梯子的长度和梯子与地面
所成角的大小(精确到
1′);
(2)如果把梯子的底端到墙角的
距离减少
0.4
米,那么梯子与地面所
成的角是多少?
A
C
B
A
C
B
解(1)梯子的长度
=
=
4(米)
sin
A
=
=
=
0.8
∴∠A
≈
53°8′
(2)如图
DE
是梯子的底端向墙角移动
0.4
米之后的情形,则
DC
=
2.4
–
0.4
=
2
米.
则
cos
D
=
=
=
0.5
∴∠D
=
60°
D
E
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第2课时
解决单一直角三角形问题
23.2
解直角三角形及其应用
沪科版
九年级数学上册
教学课件
学习目标
【知识与技能】
比较熟练的应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
【过程与方法】
通过学习进一步掌握解直角三角形的方法.
【情感态度】
培养学生把实际问题转化为数学问题的能力.
【教学重点】
应用解直角三角形的知识解决与仰角、俯角有关的实际问题.
【教学难点】
选用恰当的直角三角形,解题思路分析.
新课导入
A
C
B
a
b
c
直角三角形的边角数量关系有哪些?
a2
+
b2
=
c2
∠A
+
∠B
=
90°
sin
A
=
,sin
B
=
,
cos
A
=
,cos
B
=
,
tan
A
=
,tan
B
=
.
a
c
a
b
b
c
b
a
b
c
a
c
新课探究
解直角三角形在实际问题中有着广泛的应用.
例
3
如图,一学生要测量校园内一棵水杉树的高度.
他站在距离水杉树
8
m
的
E
处,测得树顶的仰角∠ACD
=
52°,已知测角器的架高
CE
=
1.6
m,问树高
AB
为多少米?(精确到0.1m)
E
B
D
C
A
52°
在进行高度测量时,由视线与水平线所夹的角中,当视线在水平线上方时叫做仰角;
当视线在水平线下方时叫做俯角.
铅垂线
水平线
仰角
俯角
视线
视线
E
B
D
C
A
52°
解
在Rt△ACD
中,∠ACD
=
52°,CD
=
EB
=
8
m.
由
tan
∠ACD
=
,得
AD
=
CD
·
tan
∠ACD
=
8×tan
52°
=
8×1.279
9
≈
10.2(m)
E
B
D
C
A
52°
由
DB
=
CE
=
1.6
m,得
AB
=
AD
+
DB
=
10.2
+
1.6
=
11.8(m)
答:树高
AB
为
11.8
m.
练习
如图,飞机的飞行高度
AB
=
1
000
m.
从飞机上测得到地面着陆点
C
的俯角为18°,求飞机到着陆点的距离
AC
的值(精确到
1
m).
A
B
C
18°
解
由题意得∠C
=
18°,
sin
C
=
∴AC
=
A
B
C
18°
=
≈
3236(m)
随堂演练
1.
如图,在电线杆上离地面
6
米处用拉线固定电线杆,拉线和地面之间的夹角为
60°
,求拉线AC
的长和拉线下端点
A
与线杆底部
D
的距离(精确到
0.1
米).
6
米
A
D
C
60°
B
6
米
A
D
C
B
60°
解
由
sin
A
=
,得
AC
=
=
≈
6.9(米)
由
tan
A
=
,得
AD
=
=
≈
3.5(米)
2.
如图,沿
AC
方向开山修路,为了加快施工进度,要在小山另一侧的
E
处同时施工.
如果从
AC
上取一点
B,使∠ABD
=
140°,
BD
=
520
m,∠D
=
50°,那么开挖点
E
离
点D
多远,才能使点
A,C,E
正好在一条直线上?(精确到1
m)
140°
50°
A
B
E
D
C
140°
50°
A
B
E
D
C
解
连接
CE.
∵∠ABD
=
140°,
∴∠DBE
=
180°–
140°=
40°.
∴∠E
=
180°–
40°–
50°=
90°
由
cos
D
=
,得
DE
=
BD
·
cos
D
=
520×cos
50°≈
334(m)
3.
如图,一架梯子斜靠在墙上,梯子顶端到地面的距离
BC
=
3.2
米,底端到墙根的距离
AC
=
2.4
米.
(1)求梯子的长度和梯子与地面
所成角的大小(精确到
1′);
(2)如果把梯子的底端到墙角的
距离减少
0.4
米,那么梯子与地面所
成的角是多少?
A
C
B
A
C
B
解(1)梯子的长度
=
=
4(米)
sin
A
=
=
=
0.8
∴∠A
≈
53°8′
(2)如图
DE
是梯子的底端向墙角移动
0.4
米之后的情形,则
DC
=
2.4
–
0.4
=
2
米.
则
cos
D
=
=
=
0.5
∴∠D
=
60°
D
E
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
