2020-2021学年度人教版八年级数学上册 11.2.1 三角形的内角课时练习(含解析)
文档属性
| 名称 | 2020-2021学年度人教版八年级数学上册 11.2.1 三角形的内角课时练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 781.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 19:46:27 | ||
图片预览




文档简介
2020-2021学年度人教版八年级数学上册11.2.1三角形的内角课时练习
一、选择题
1.将一副三角尺按如图所示的方式摆放(两条直角边在同一条直线上),连接另外两个锐角顶点,并测得false,则false的度数为( )
A.false B.false C.false D.false
2.如图,已知false为false三边垂直平分线的交点,且false,则false的度数为( )
A.false B.false C.false D.false
3.下列命题中:
①内错角相等;
②两点之间线段最短;
③直角三角形两锐角互余;
④两条平行线被第三条直线所截,所得的一组内错角的角平分线互相平行.
属于真命题的有( )
A.1个 B.2个 C.3个 D.4个
4.在一个三角形的三个外角中,钝角的个数最多有( )
A.3个 B.2个 C.1个 D.0个
5.如图,false,false,则false的度数是( ).
A.35° B.55° C.65° D.75°
6.在false中,false,点false在false边上,连接false,若false是直角三角形,则false的度数是( )
A.false B.false C.false D.false或false
7.一副三角板如图摆放(直角顶点false重合),边false与false交于点false,则false( )
A.false B.false C.false D.false
8.已知:如图,AB⊥CD于O,EF为经过点O的一条直线,那么∠1与∠2的关系是( )
A.互为对顶角 B.互补 C.互余 D.相等
9.如图,在Rt△ABC中,过顶点C作l∥AB,若∠1=25°,则∠2的度数为( )
A.35° B.45° C.55° D.65°
10.如图,在四边形ABCD中,∠ABC与∠BCD的平分线的交点E恰好在AD边上,则∠BEC=( )
A.∠A+∠D﹣45° B.false(∠A+∠D)+45°
C.180°﹣(∠A+∠D) D.false∠A+false∠D
二、填空题
11.如图,在△ABC中,∠A=20°,∠ABC与∠ACB的平分线交于点D1,∠ABD1与∠ACD1的平分线交于点D2,以此类推,∠ABD2与∠ACD2的平分线交于点D,则∠BDC的度数是__.
12.如图,在false中,false度,false与false的平分线交于点false,则false______度;false与false的平分线交于点false,得false;…false与false的平分线交于点false,得false.则false______度.
13.在false中,false,若false,则false的度数是________.
14.如图,BE、CF是△ABC的角平分线,∠BAC=80°,BE、CF相交于D,则∠BDC的度数是_______.
15.已知在false中,false,false是false的高,false,则false_________.
16.△ABC 中,BD 是 AC 边上的高,∠A=30°,∠DBC=40°,则∠ABC=_____度.
17.在△ABC中,∠A=60°,∠B=40°,则∠C的度数是_____.
18.如图,AB∥CD,FE⊥DB,垂足为点E,∠2=40°,则∠1的度数是______.
19.如图,在△ABC中,D,E分别是边AB,AC上一点,将△ABC沿DE折叠,使点A的对称点A'落在边BC上,若∠A=50°,则∠1+∠2+∠3+∠4=______.
20.将一副直角三角尺按如图所示摆放,则图中false的度数是______.
三、解答题
21.如图,四边形false中,作点false,设false分别与false、false交于点false、false.若false平分false,且false,求证:false.
完成下面的证明过程:
证明:false (已知) .
false(垂直的定义).
false平分false (已知)
false ( )
false (已知)
false (等量代换)
falsefalse ( )
false false(两直线平行,内错角相等)
false(直角三角形的两个锐角互余)
同理由false,
可得false
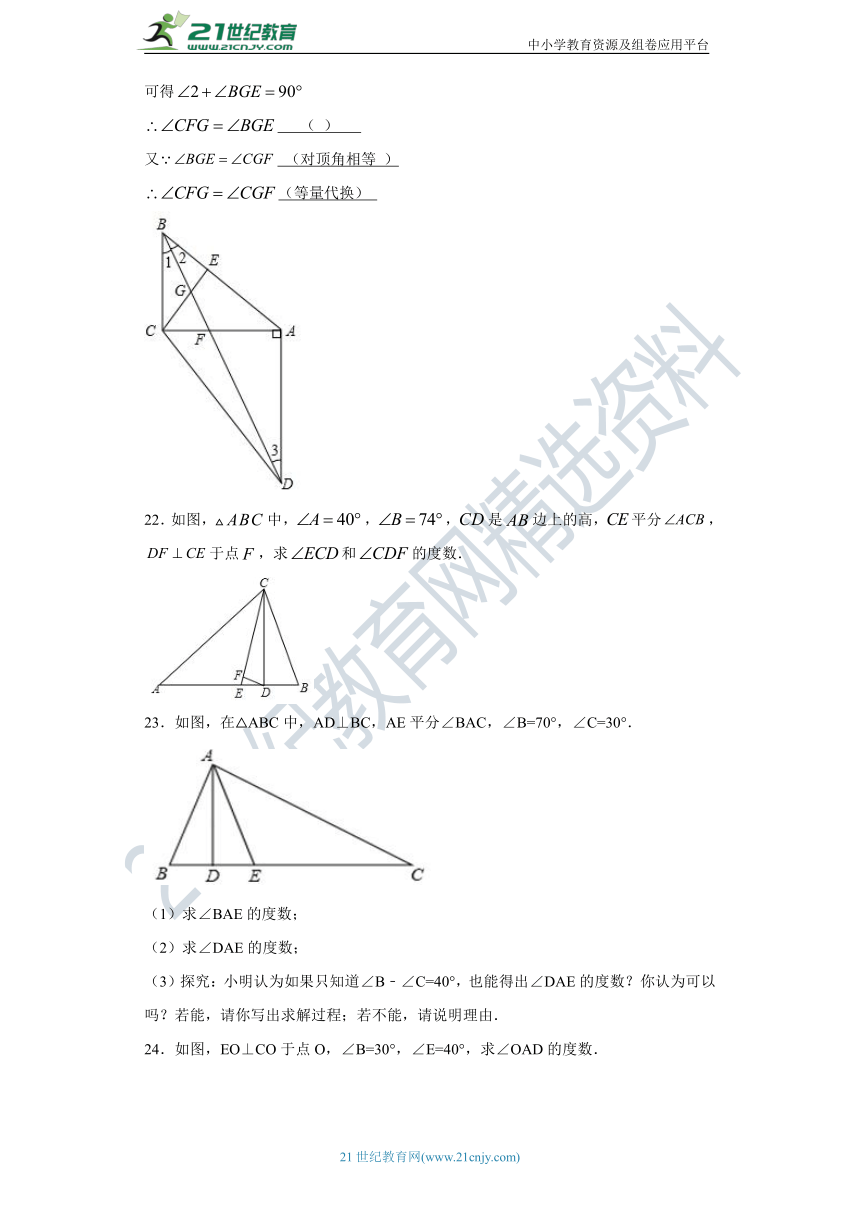
false ( )
又false (对顶角相等 )
false(等量代换)
22.如图,false中,false,false,false是false边上的高,false平分false,false于点false,求false和false的度数.
23.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.
(1)求∠BAE的度数;
(2)求∠DAE的度数;
(3)探究:小明认为如果只知道∠B﹣∠C=40°,也能得出∠DAE的度数?你认为可以吗?若能,请你写出求解过程;若不能,请说明理由.
24.如图,EO⊥CO于点O,∠B=30°,∠E=40°,求∠OAD的度数.
25.如图所示,有一块直角三角板false(足够大),其中false,把直角三角板false放置在锐角false上,三角板false的两边false恰好分别经过false.
(1)若false,则false °,false °,
false °.
(2)若false则false °.
(3)请你猜想一下false与false所满足的数量关系 .
26.问题情景:如图1,在同一平面内,点false和点false分别位于一块直角三角板false的两条直角边false,false上,点false与点false在直线false的同侧,若点false在false内部,试问false,false与false的大小是否满足某种确定的数量关系?
(1)特殊探究:若false,则false_________度,false________度,false_________度;
(2)类比探索:请猜想false与false的关系,并说明理由;
(3)类比延伸:改变点false的位置,使点false在false外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出false,false与false满足的数量关系式.
27.求出下列图形中的x的值:
28.如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.
29.如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若=60°,∠BED=70°.求∠ABC和∠BAC的度数.
30.如图,已知:在Rt△ABC中,∠C=90°,BD平分∠ABC且交AC于D.
(1)若∠BAC=30°,求证:AD=BD;
(2)若AP平分∠BAC且交BD于P,求∠BPA的度数
参考答案
1.D
【解析】
【分析】
如图,先根据三角板的各角的度数和平角可求出∠ACE,再根据三角形的内角和180°即可解答.
【详解】
∵∠ACB=60°,∠DCE=45°,
∴∠ACE=180°-60°-45°=75°,
∵∠1=45°,
∴∠2=180°-45°-75°=60°,
故选:D.
【点睛】
本题考查直角三角板的角度计算、三角形的内角和定理,熟知三角板的各角度数,掌握三角形的内角和为180°是解答的关键.
2.B
【解析】
【分析】
延长AO交BC于D,根据垂直平分线的性质可得到AO=BO=CO,再根据等边对等角的性质得到∠OAB=∠OBA,∠OAC=∠OCA,再由三角形的外角性质可求得∠BOD=∠OAB+∠OBA,∠COD=∠OAC+∠OCA,从而不难求得∠BOC的度数.
【详解】
延长AO交BC于D.
∵点O在AB的垂直平分线上.
∴AO=BO.
同理:AO=CO.
∴∠OAB=∠OBA,∠OAC=∠OCA.
∵∠BOD=∠OAB+∠OBA,∠COD=∠OAC+∠OCA.
∴∠BOD=2∠OAB,∠COD=2∠OAC.
∴∠BOC=∠BOD+∠COD=2∠OAB+2∠OAC=2(∠OAB+∠OAC)=2∠BAC.
∵∠A=50°.
∴∠BOC=100°.
故选:B.
【点睛】
此题主要考查:(1)线段垂直平分线的性质:垂直平分线上任意一点,到线段两端点的距离相等.(2)三角形的外角性质:三角形的一个外角等于和它不相邻的两个内角的和.
3.C
【解析】
【分析】
根据平行线的性质、直角三角形的性质判断即可.
【详解】
解:①两直线平行,内错角相等,本说法是假命题;
②两点之间线段最短,本说法是真命题;
③直角三角形两锐角互余,本说法是真命题;
④两条平行线被第三条直线所截,所得的一组内错角的角平分线互相平行,本说法是真命题;
故选:C.
【点睛】
本题主要考查证明与命题、平行线的性质及直角三角形的性质,关键是熟记概念进行判断.
4.A
【解析】
【分析】
在锐角三角形的外角中,有三个钝角;在直角三角形外角中,有两个钝角;在钝角三角形外角中,有两个钝角.综上可知,在三角形的三个外角中,钝角的个数最多有3个.
【详解】
解:根据三角形的内角和是180度可知:三角形的三个内角中最多可有3个锐角,
所以对应的在三角形的三个外角中,钝角的个数最多有3个.
故选A.
【点睛】
本题主要考查了三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和.(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.
5.A
【解析】
【分析】
根据题意及三角形内角和可得∠D=∠A,故问题得解.
【详解】
解:false∠AOB=∠DOC,false,
falsefalse,
falsefalse,
falsefalse,
falsefalse;
故选A.
【点睛】
本题主要考查三角形内角和,熟练掌握三角形的内角和是解题的关键.
6.D
【解析】
【分析】
分两种情况讨论:当false或false时,分别画出相应图形,结合三角形内角和180°解题即可.
【详解】
分两种情况讨论:
(1)如图1,当false时,
false
false;
(2)如图2,当false时,
false
false
false
综上所述,false的度数为60°或15°
故选:D
【点睛】
本题考查三角形内角和定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.
7.A
【解析】
【分析】
由题意知图中是一个等腰直角三角形和一个含false角的直角三角形,故false,false,由平行线的性质可知false,由三角形内角和定理可求出false的度数.
【详解】
由题意知false,false,
∵false,
∴false,
在false中,
falsefalse,
故选A.
【点睛】
本题考查了特殊直角三角形的性质,平行线的性质,三角形内角和定理等,解题关键是要搞清楚一副三角板是指一个等腰直角三角形和一个含false角的直角三角形.
8.C
【解析】
【分析】
根据垂线的定义得出∠BOD=90°;然后由平角的定义来求∠1与∠2的关系.
【详解】
解:∵AB⊥CD,
∴∠BOD=90°.
又∵EF为过点O的一条直线,
∴∠1+∠2=180°﹣∠BOD=90°,
即:∠1与∠2互余,
故选:C.
【点睛】
本题考查了垂线的定义、平角的定义、角的互余关系;熟练掌握垂线的定义和平角的定义是解题的关键.
9.D
【解析】
【分析】
由三角形是直角三角形,得∠2+∠A=90?,而l∥AB ,可求∠A,再计算可求.
【详解】
∵l∥AB,
∴∠A=∠1(两直线平行,内错角相等),
∵∠1=25°,
∴∠A=25°,
在Rt△ACB中,∠ACB=90°,
∴∠2=180°﹣∠ACB﹣∠A=180°﹣90°﹣25°=65°,
故选择:D.
【点睛】
本题考查求角度问题,关键抓住直角三角形两锐角互余,两直线平行,内错角相等.
10.D
【解析】
【分析】
根据四边形的内角和, ∠ABC+∠BCD=360°﹣(∠A+∠D),根据角平分线的定义可得false 再根据三角形的内角和定理可得false 然后整理即可得解;
【详解】
∵四边形的内角和=360°,
∴∠ABC+∠BCD=360°﹣(∠A+∠D),
∵∠ABC与∠BCD的平分线的交点E恰好在AD边上,
∴false
∴
false
∴∠BEC=180°﹣(∠EBC+∠ECB)
false
false
故选D.
【点睛】
考查四边形的内角和,三角形的内角和以及角平分线的性质,掌握角平分线的性质是解题的关键.
11.40°.
【解析】
【分析】
根据题意可得∠ABC+∠ACB=160°,BD1,CD1,CD2,BD2…BDn,CDn是角平分线,可得∠ABDn+∠ACDn=160×(false)n,可求∠BCDn+∠CBDn的值,再根据三角形内角和定理可求结果.
【详解】
∵∠A=20°,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=160°,
∵BD1平分∠ABC,CD1平分∠ACB,
∴∠ABD1=false∠ABC,∠ACD1=false∠ACD,
∵BD2平分∠ABD1,CD2平分∠ACD1,
∴∠ABD2=false∠ABD1=false∠ABC,∠ACD2=false∠ACD1=false∠ACB,
同理可得∠ABD=false∠ABC,∠ACD=false∠ACB,
∴∠ABD+∠ACD=160°×false=20°,
∴∠BCD+∠CBD=140°
∴∠BDC=180﹣∠BCD﹣∠CBD=40°
故答案为40°.
【点睛】
本题考查了三角形内角和定理,角平分线,关键是找出其中的规律,利用规律解决问题.
12.falseβ, falseβ
【解析】
【分析】
已知∠A,求∠A1,利用外角定理可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,把∠ACD利用角平分线转成2∠A1CD,∠ABC转成2∠A1BC,消去∠A1BC,∠A1CD即可,再用类似的办法求∠A2,以此类推即可
【详解】
∵BA1平分∠ABC,CA1平分∠A1CD,
∴∠AB A1=∠A1BC=false∠ABC,∠AC A1=∠A1CD=false∠ACD,
由三角形的外角得
∴∠A1CD=∠A1+∠A1BC,
∴∠A1CD=∠A1+∠A1BC①
∴2∠A1CD=∠A+2∠A1BC②
把①代入②得∠A1=false∠A=falseβ
CA2平分∠A2CD,
∠A2C A1=∠A2CD=false∠A1CD,
由三角形的外角得
∴∠A1CD=∠A1+∠A1BC,
∴∠A2CD=∠A2+∠A2BC③
∴2∠A2CD=∠A1+2∠A2BC④
解得∠A2=false∠A1,
∠A2=false∠A1false∠A=falseβ=falseβ
同理
∠A3=false∠A2=false∠A=falseβ=falseβ
…
∠A2019= falseβ
故答案为:①falseβ,②falseβ
【点睛】
本题考查(第二内角的)外角平分线与(第一)内角平分线所夹的角问题,找到两平分线的夹角与第三个角的关系是解决问题关键
13.25°
【解析】
【分析】
根据三角形的内角和即可求解.
【详解】
∵在false中,false, false,
∴∠A=180°-∠C-∠B=25°
故答案为:25°.
【点睛】
此题主要考查三角形的角度求解,解题的关键是熟知三角形的内角和为180°.
14.false
【解析】
【分析】
由false、false是false的角平分线,∠BAC=80°,根据三角形内角和定理,可求得false,根据角平分线的定义,可得false,进而解答即可.
【详解】
解:false
false
false、false是false的角平分线,
false,false,
false
false.
故答案为:false.
【点睛】
此题考查了三角形内角和定理以及角平分线的定义.此题难度不大,注意掌握数形结合思想和整体思想的应用.
15.80或100
【解析】
【分析】
根据题意画出图形,当△ABC为锐角三角形或钝角三角形两种情况解答,结合已知条件即可得出∠ABC的度数.
【详解】
(1)如图,当△ABC为锐角三角形时,
∠ACB=∠BCD=80°;
(2)如图,当△ABC为钝角三角形时,
∠ACB=180°-∠BCD=100°.
故答案为:80°或100.
【点睛】
本题考查了三角形内角和定理的应用,关键在于根据题意画出图形,分别进行讨论解答.
16.100或20
【解析】
【分析】
根据BD的不同位置,分两种情况进行讨论:BD在△ABC内部,BD在△ABC外部,分别进行画图计算即可.
【详解】
如图,当BD在△ABC内部时,
∠ABC=∠ABD+∠DBC=90°-∠A +∠DBC=60°+40°=100°;
如图,当BD在△ABC外部时,
∠ABC=∠ABD-∠DBC=90°-∠A -∠DBC =60°-40°=20°;
故答案为:100或20.
【点睛】
本题主要考查了三角形的内角和定理,解决问题的关键是掌握三角形的内角和等于180°,解题时注意分类思想的运用.
17.80°
【解析】
【分析】
三角形内角和是180°,根据三角形内角和定理计算即可.
【详解】
由三角形内角和定理得:
∠C=180°-∠A-∠B=80°,
故答案为80°.
【点睛】
本题考查的是三角形内角和定理的应用,掌握三角形内角和等于180°是解题的关键.
18.50°
【解析】
【分析】
根据平行线的性质求出∠EDF=∠2=40°,根据垂直求出∠FED=90°,根据三角形内角和定理求出即可.
【详解】
解:∵AB∥CD,∠2=40°,
∴∠EDF=∠2=40°,
∵FE⊥DB,
∴∠FED=90°,
∠1=180°-∠FED-∠EDF=180°-90°-40°=50°,
故答案为50°.
【点睛】
本题考查了三角形内角和定理,垂直定义,平行线的性质等知识点,能根据平行线的性质求出∠EDF的度数是解此题的关键.
19.230°
【解析】
【分析】
依据三角形内角和定理,可得△ABC中,∠B+∠C=130°,再根据∠1+∠2+∠B=180°,∠3+∠4+∠C=180°,即可得出∠1+∠2+∠3+∠4=360°﹣(∠B+∠C)=230°.
【详解】
解:∵∠A=50°,
∴△ABC中,∠B+∠C=130°,
又∵∠1+∠2+∠B=180°,∠3+∠4+∠C=180°,
∴∠1+∠2+∠3+∠4=360°﹣(∠B+∠C)=360°﹣130°=230°,
故答案为:230°.
【点睛】
本题主要考查三角形内角和,熟练掌握三角形内角和及角之间的等量关系是解题的关键.
20.false
【解析】
【分析】
根据直角三角板false,false,false,再根据角的和差关系可得false的度数,再利用三角形内角和为false计算出false的度数.
【详解】
解:根据直角三角板false,false,false,
false,
false,
false,
故答案为false.
【点睛】
此题主要考查了三角形内角和定理,以及角的计算,关键是掌握三角形内角和为false,正确计算出false的度数.
21.角平分线定义;false;内错角相等,两直线平行;false;等角的余角相等
【解析】
【分析】
根据垂直的定义可得false,然后根据角平分线定义可得false,根据等量代换可得false∠3,再根据内错角相等,两直线平行可证false,从而得出∠ACB false,再根据等角的余角相等可得false,最后根据对顶角相等和等量代换即可证出结论.
【详解】
证明:false (已知) .
false(垂直的定义).
false平分false (已知)
false(角平分线定义)
false (已知)
false∠3(等量代换)
falsefalse(内错角相等,两直线平行)
false ∠ACB false(两直线平行,内错角相等)
false(直角三角形的两个锐角互余)
同理由false,
可得false
false(等角的余角相等)
又false (对顶角相等 )
false(等量代换)
故答案为: 角平分线定义;false;内错角相等,两直线平行;false;等角的余角相等.
【点睛】
此题考查的是垂直定义、角平分线的定义、直角三角形的性质和平行线的判定及性质,掌握垂直定义、角平分线的定义、直角三角形的性质和平行线的判定及性质是解题关键.
22.∠ECD=17°,∠CDF=73°.
【解析】
【分析】
根据三角形内角和定理求出∠ACB,根据角平分线定义求出∠BCE即可,根据直角三角形两锐角互余求出∠BCD,进而求出∠ECD,再根据直角三角形两锐角互余求出∠CDF即可.
【详解】
解:∵∠A+∠B+∠ACB=180°,∠A=40°,∠B=74°,
∴∠ACB=66°.
∵CE平分∠ACB,
∴∠BCEfalse∠ACBfalse66°=33°.
∵CD⊥AB,
∴∠CDB=90°.
∴∠BCD=90°﹣74°=16°,
∴∠ECD=∠BCE﹣∠BCD=17°.
∵DF⊥CE,
∴∠CFD=90°,
∴∠CDF=90°﹣∠ECD=73°,
即∠ECD=17°,∠CDF=73°.
【点睛】
本题考查了三角形的内角和定理,直角三角形两锐角互余,垂直定义,角平分线定义等知识点,关键是求出各个角的度数.
23.(1)false;(2)false;(3)可以,见解析
【解析】
【分析】
(1)false平分false,可知∠BAE=∠CAE,由三角形内角和可求∠BAC即可,
(2)由AD⊥BC,可求false,由角和差知∠DAE=∠BAE-∠BAD即可,
(3)先求出∠BAC=180゜-∠B-∠C,再求其一半∠BAE,由△ABD,∠BAD=90゜-∠B,作差∠BAE-∠BAD计算即可.
【详解】
解:(1)∵false,
∴false,
∵false平分false
∴false,
(2)∵false于点false,
∴false
∴false,
∴false,
(3)可以.理由如下:
∵false平分false
∴false,
∵false于点false
∴false
∴false,
∴false,
∵false,
∴false.
【点睛】
本题考查角度的规律求法问题,掌握三角形的内角和,角平分线,直角三角形两锐角互余知识是解题关键.
24.20°
【解析】
试题分析:利用三角形外角性质可以得到∠ODB的度数,再利用三角形内角和定理得到∠OAD的度数.
试题解析:
∵∠B=30°,∠E=40°,
∴∠ADO=∠B +∠E =30°+40°=70°,
∵EO⊥CO于点O,
∴∠O=90°,
∴∠OAD=180°-∠O-∠ADO
=180°-90°-70°
=20°.
25.(1)140,90,50;(2)35;(3)false
【解析】
【分析】
(1)根据三角形内角和定理可得∠ABC+∠ACB=180°-∠A=140°,∠DBC+∠DCB=180°-∠DBC=90°,进而可求出∠ABD+∠ACD的度数;
(2)根据三角形内角和定理可得∠ABC+∠ACB=180°-∠A=130°,∠DBC+∠DCB=180°-∠DBC=90°,进而可求出∠ABD+∠ACD的度数;
(3)根据三角形内角和定义有90°+(∠ABD+∠ACD)+∠A=180°,则∠ABD+∠ACD=90°-∠A.
【详解】
解:(1)在△ABC中,∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°,
在△DBC中,∵∠BDC=90°,
∴∠DBC+∠DCB=180°-90°=90°,
∴∠ABD+∠ACD=140°-90°=50°;
故答案为:140;90;50.
(2)在△ABC中,∵∠A=55°,
∴∠ABC+∠ACB=180°-55°=125°,
在△DBC中,∵∠BDC=90°,
∴∠DBC+∠DCB=180°-90°=90°,
∴∠ABD+∠ACD=125°-90°=35°,
故答案为:35;
(3)∠ABD+∠ACD与∠A之间的数量关系为:∠ABD+∠ACD=90°-∠A.证明如下:
在△ABC中,∠ABC+∠ACB=180°-∠A.
在△DBC中,∠DBC+∠DCB=90°.
∴∠ABC+∠ACB-(∠DBC+∠DCB)=180°-∠A-90°.
∴∠ABD+∠ACD=90°-∠A,
故答案为:∠ABD+∠ACD=90°-∠A.
【点睛】
本题考查了三角形的内角和定理,熟练掌握三角形的内角和定理是解答的关键.
26.(1)125,90,35;(2)∠ABP+∠ACP=90°-∠A,证明见解析;(3)结论不成立.∠ABP-∠ACP=90°-∠A,∠ABP+∠ACP=∠A-90°或∠ACP - ∠ABP =90°-∠A.
【解析】
【分析】
(1)根据三角形内角和即可得出∠ABC+∠ACB,∠PBC+∠PCB,然后即可得出∠ABP+∠ACP;
(2)根据三角形内角和定理进行等量转换,即可得出∠ABP+∠ACP=90°-∠A;
(3)按照(2)中同样的方法进行等量转换,求解即可判定.
【详解】
(1)∠ABC+∠ACB=180°-∠A=180°-55°=125度,∠PBC+∠PCB=180°-∠P=180°-90°=90度,
∠ABP+∠ACP=∠ABC+∠ACB -(∠PBC+∠PCB)=125°-90°=35度;
(2)猜想:∠ABP+∠ACP=90°-∠A;
证明:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵∠ABC=∠ABP+∠PBC,∠ACB=∠ACP+∠PCB,
∴(∠ABP+∠PBC)+(∠ACP+∠PCB)=180°-∠A,
∴(∠ABP+∠ACP)+(∠PBC+∠PCB)=180°-∠A,
又∵在Rt△PBC中,∠P=90°,
∴∠PBC+∠PCB=90°,
∴(∠ABP+∠ACP)+90°=180°-∠A,
∴∠ABP+∠ACP=90°-∠A.
(3)判断:(2)中的结论不成立.
证明:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵∠ABC=∠PBC-∠ABP,∠ACB=∠PCB-∠ACP,
∴(∠PBC+∠PCB)-(∠ABP+∠ACP)=180°-∠A,
又∵在Rt△PBC中,∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABP-∠ACP=90°-∠A,∠ABP+∠ACP=∠A-90°
或∠ACP - ∠ABP =90°-∠A.
【点睛】
此题主要考查利用三角形内角和定理进行等角转换,熟练掌握,即可解题.
27.40;50
【解析】
【分析】
根据三角形内角和定理求解.
【详解】
解:在△ABC中,∠A+∠B+∠C=180°,
∵∠B=40°, ∠C=70°,
∴∠A=180°-∠B-∠C=180°-40°-70°=70°,
∴x=40;
在△ABC中,∠A+∠B+∠C=180°,
∵∠A=80°,
∴80°+x°+x° =180°,
∴x=50.
【点睛】
本题考查三角形的内角和定理,应用内角和定理求角的大小是解答此题的重要途径.
28.83°
【解析】
【分析】
根据对顶角相等,三角形内角和定理解答.
【详解】
解:∵DF⊥AB,
∴∠AFE=90°,
∴∠AEF=90°?∠A=90°?35°=55°,
∴∠CED=∠AEF=55°,
∴∠ACD=180°?∠CED?∠D=180°?55°?42°=83°.
【点睛】
本题考查对顶角的性质,三角形内角和定理:三角形的三个内角和为180°.
29.40°;80°
【解析】
分析:先根据AD是△ABC的高得出∠ADB=90°,再由三角形内角和定理及三角形外角的性质可知∠DBE+∠ADB+∠BED=180°,故∠DBE=180°-∠ADB-∠BED=20°.根据BE平分∠ABC得出∠ABC=2∠DBE=40°.?根据∠BAC+∠ABC+∠C=180°,∠C=60°即可得出结论.
详解:∵AD是△ABC的高,
∴∠ADB=90°.
又∵∠DBE+∠ADB+∠BED=180°,∠BED=70°,
∴∠DBE=180°-∠ADB-∠BED=20°.
∵BE平分∠ABC,
∴∠ABC=2∠DBE=40°.?
又∵∠BAC+∠ABC+∠C=180°,∠C=60°,
∴∠BAC=180°-∠ABC-∠C=80°.
点睛:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
30.(1)见解析
(2)135°
【解析】
【分析】
(1)根据直角三角形两锐角互余和角平分线的定义,可以得到角相等,进而得到两边相等;
(2)由三角形的外角性质和内角和定理即可求解.
【详解】
(1)证明:false
又因为BD平分∠ABC,所以false
(2)解:false
一、选择题
1.将一副三角尺按如图所示的方式摆放(两条直角边在同一条直线上),连接另外两个锐角顶点,并测得false,则false的度数为( )
A.false B.false C.false D.false
2.如图,已知false为false三边垂直平分线的交点,且false,则false的度数为( )
A.false B.false C.false D.false
3.下列命题中:
①内错角相等;
②两点之间线段最短;
③直角三角形两锐角互余;
④两条平行线被第三条直线所截,所得的一组内错角的角平分线互相平行.
属于真命题的有( )
A.1个 B.2个 C.3个 D.4个
4.在一个三角形的三个外角中,钝角的个数最多有( )
A.3个 B.2个 C.1个 D.0个
5.如图,false,false,则false的度数是( ).
A.35° B.55° C.65° D.75°
6.在false中,false,点false在false边上,连接false,若false是直角三角形,则false的度数是( )
A.false B.false C.false D.false或false
7.一副三角板如图摆放(直角顶点false重合),边false与false交于点false,则false( )
A.false B.false C.false D.false
8.已知:如图,AB⊥CD于O,EF为经过点O的一条直线,那么∠1与∠2的关系是( )
A.互为对顶角 B.互补 C.互余 D.相等
9.如图,在Rt△ABC中,过顶点C作l∥AB,若∠1=25°,则∠2的度数为( )
A.35° B.45° C.55° D.65°
10.如图,在四边形ABCD中,∠ABC与∠BCD的平分线的交点E恰好在AD边上,则∠BEC=( )
A.∠A+∠D﹣45° B.false(∠A+∠D)+45°
C.180°﹣(∠A+∠D) D.false∠A+false∠D
二、填空题
11.如图,在△ABC中,∠A=20°,∠ABC与∠ACB的平分线交于点D1,∠ABD1与∠ACD1的平分线交于点D2,以此类推,∠ABD2与∠ACD2的平分线交于点D,则∠BDC的度数是__.
12.如图,在false中,false度,false与false的平分线交于点false,则false______度;false与false的平分线交于点false,得false;…false与false的平分线交于点false,得false.则false______度.
13.在false中,false,若false,则false的度数是________.
14.如图,BE、CF是△ABC的角平分线,∠BAC=80°,BE、CF相交于D,则∠BDC的度数是_______.
15.已知在false中,false,false是false的高,false,则false_________.
16.△ABC 中,BD 是 AC 边上的高,∠A=30°,∠DBC=40°,则∠ABC=_____度.
17.在△ABC中,∠A=60°,∠B=40°,则∠C的度数是_____.
18.如图,AB∥CD,FE⊥DB,垂足为点E,∠2=40°,则∠1的度数是______.
19.如图,在△ABC中,D,E分别是边AB,AC上一点,将△ABC沿DE折叠,使点A的对称点A'落在边BC上,若∠A=50°,则∠1+∠2+∠3+∠4=______.
20.将一副直角三角尺按如图所示摆放,则图中false的度数是______.
三、解答题
21.如图,四边形false中,作点false,设false分别与false、false交于点false、false.若false平分false,且false,求证:false.
完成下面的证明过程:
证明:false (已知) .
false(垂直的定义).
false平分false (已知)
false ( )
false (已知)
false (等量代换)
falsefalse ( )
false false(两直线平行,内错角相等)
false(直角三角形的两个锐角互余)
同理由false,
可得false
false ( )
又false (对顶角相等 )
false(等量代换)
22.如图,false中,false,false,false是false边上的高,false平分false,false于点false,求false和false的度数.
23.如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.
(1)求∠BAE的度数;
(2)求∠DAE的度数;
(3)探究:小明认为如果只知道∠B﹣∠C=40°,也能得出∠DAE的度数?你认为可以吗?若能,请你写出求解过程;若不能,请说明理由.
24.如图,EO⊥CO于点O,∠B=30°,∠E=40°,求∠OAD的度数.
25.如图所示,有一块直角三角板false(足够大),其中false,把直角三角板false放置在锐角false上,三角板false的两边false恰好分别经过false.
(1)若false,则false °,false °,
false °.
(2)若false则false °.
(3)请你猜想一下false与false所满足的数量关系 .
26.问题情景:如图1,在同一平面内,点false和点false分别位于一块直角三角板false的两条直角边false,false上,点false与点false在直线false的同侧,若点false在false内部,试问false,false与false的大小是否满足某种确定的数量关系?
(1)特殊探究:若false,则false_________度,false________度,false_________度;
(2)类比探索:请猜想false与false的关系,并说明理由;
(3)类比延伸:改变点false的位置,使点false在false外,其它条件都不变,判断(2)中的结论是否仍然成立?若成立,请说明理由;若不成立,请直接写出false,false与false满足的数量关系式.
27.求出下列图形中的x的值:
28.如图,已知D为△ABC边BC延长线上一点,DF⊥AB于F交AC于E,∠A=35°,∠D=42°,求∠ACD的度数.
29.如图,AD是△ABC边BC上的高,BE平分∠ABC交AD于点E.若=60°,∠BED=70°.求∠ABC和∠BAC的度数.
30.如图,已知:在Rt△ABC中,∠C=90°,BD平分∠ABC且交AC于D.
(1)若∠BAC=30°,求证:AD=BD;
(2)若AP平分∠BAC且交BD于P,求∠BPA的度数
参考答案
1.D
【解析】
【分析】
如图,先根据三角板的各角的度数和平角可求出∠ACE,再根据三角形的内角和180°即可解答.
【详解】
∵∠ACB=60°,∠DCE=45°,
∴∠ACE=180°-60°-45°=75°,
∵∠1=45°,
∴∠2=180°-45°-75°=60°,
故选:D.
【点睛】
本题考查直角三角板的角度计算、三角形的内角和定理,熟知三角板的各角度数,掌握三角形的内角和为180°是解答的关键.
2.B
【解析】
【分析】
延长AO交BC于D,根据垂直平分线的性质可得到AO=BO=CO,再根据等边对等角的性质得到∠OAB=∠OBA,∠OAC=∠OCA,再由三角形的外角性质可求得∠BOD=∠OAB+∠OBA,∠COD=∠OAC+∠OCA,从而不难求得∠BOC的度数.
【详解】
延长AO交BC于D.
∵点O在AB的垂直平分线上.
∴AO=BO.
同理:AO=CO.
∴∠OAB=∠OBA,∠OAC=∠OCA.
∵∠BOD=∠OAB+∠OBA,∠COD=∠OAC+∠OCA.
∴∠BOD=2∠OAB,∠COD=2∠OAC.
∴∠BOC=∠BOD+∠COD=2∠OAB+2∠OAC=2(∠OAB+∠OAC)=2∠BAC.
∵∠A=50°.
∴∠BOC=100°.
故选:B.
【点睛】
此题主要考查:(1)线段垂直平分线的性质:垂直平分线上任意一点,到线段两端点的距离相等.(2)三角形的外角性质:三角形的一个外角等于和它不相邻的两个内角的和.
3.C
【解析】
【分析】
根据平行线的性质、直角三角形的性质判断即可.
【详解】
解:①两直线平行,内错角相等,本说法是假命题;
②两点之间线段最短,本说法是真命题;
③直角三角形两锐角互余,本说法是真命题;
④两条平行线被第三条直线所截,所得的一组内错角的角平分线互相平行,本说法是真命题;
故选:C.
【点睛】
本题主要考查证明与命题、平行线的性质及直角三角形的性质,关键是熟记概念进行判断.
4.A
【解析】
【分析】
在锐角三角形的外角中,有三个钝角;在直角三角形外角中,有两个钝角;在钝角三角形外角中,有两个钝角.综上可知,在三角形的三个外角中,钝角的个数最多有3个.
【详解】
解:根据三角形的内角和是180度可知:三角形的三个内角中最多可有3个锐角,
所以对应的在三角形的三个外角中,钝角的个数最多有3个.
故选A.
【点睛】
本题主要考查了三角形的内角和外角之间的关系.(1)三角形的外角等于与它不相邻的两个内角和.(2)三角形的内角和是180度.求角的度数常常要用到“三角形的内角和是180°这一隐含的条件.
5.A
【解析】
【分析】
根据题意及三角形内角和可得∠D=∠A,故问题得解.
【详解】
解:false∠AOB=∠DOC,false,
falsefalse,
falsefalse,
falsefalse,
falsefalse;
故选A.
【点睛】
本题主要考查三角形内角和,熟练掌握三角形的内角和是解题的关键.
6.D
【解析】
【分析】
分两种情况讨论:当false或false时,分别画出相应图形,结合三角形内角和180°解题即可.
【详解】
分两种情况讨论:
(1)如图1,当false时,
false
false;
(2)如图2,当false时,
false
false
false
综上所述,false的度数为60°或15°
故选:D
【点睛】
本题考查三角形内角和定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.
7.A
【解析】
【分析】
由题意知图中是一个等腰直角三角形和一个含false角的直角三角形,故false,false,由平行线的性质可知false,由三角形内角和定理可求出false的度数.
【详解】
由题意知false,false,
∵false,
∴false,
在false中,
falsefalse,
故选A.
【点睛】
本题考查了特殊直角三角形的性质,平行线的性质,三角形内角和定理等,解题关键是要搞清楚一副三角板是指一个等腰直角三角形和一个含false角的直角三角形.
8.C
【解析】
【分析】
根据垂线的定义得出∠BOD=90°;然后由平角的定义来求∠1与∠2的关系.
【详解】
解:∵AB⊥CD,
∴∠BOD=90°.
又∵EF为过点O的一条直线,
∴∠1+∠2=180°﹣∠BOD=90°,
即:∠1与∠2互余,
故选:C.
【点睛】
本题考查了垂线的定义、平角的定义、角的互余关系;熟练掌握垂线的定义和平角的定义是解题的关键.
9.D
【解析】
【分析】
由三角形是直角三角形,得∠2+∠A=90?,而l∥AB ,可求∠A,再计算可求.
【详解】
∵l∥AB,
∴∠A=∠1(两直线平行,内错角相等),
∵∠1=25°,
∴∠A=25°,
在Rt△ACB中,∠ACB=90°,
∴∠2=180°﹣∠ACB﹣∠A=180°﹣90°﹣25°=65°,
故选择:D.
【点睛】
本题考查求角度问题,关键抓住直角三角形两锐角互余,两直线平行,内错角相等.
10.D
【解析】
【分析】
根据四边形的内角和, ∠ABC+∠BCD=360°﹣(∠A+∠D),根据角平分线的定义可得false 再根据三角形的内角和定理可得false 然后整理即可得解;
【详解】
∵四边形的内角和=360°,
∴∠ABC+∠BCD=360°﹣(∠A+∠D),
∵∠ABC与∠BCD的平分线的交点E恰好在AD边上,
∴false
∴
false
∴∠BEC=180°﹣(∠EBC+∠ECB)
false
false
故选D.
【点睛】
考查四边形的内角和,三角形的内角和以及角平分线的性质,掌握角平分线的性质是解题的关键.
11.40°.
【解析】
【分析】
根据题意可得∠ABC+∠ACB=160°,BD1,CD1,CD2,BD2…BDn,CDn是角平分线,可得∠ABDn+∠ACDn=160×(false)n,可求∠BCDn+∠CBDn的值,再根据三角形内角和定理可求结果.
【详解】
∵∠A=20°,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=160°,
∵BD1平分∠ABC,CD1平分∠ACB,
∴∠ABD1=false∠ABC,∠ACD1=false∠ACD,
∵BD2平分∠ABD1,CD2平分∠ACD1,
∴∠ABD2=false∠ABD1=false∠ABC,∠ACD2=false∠ACD1=false∠ACB,
同理可得∠ABD=false∠ABC,∠ACD=false∠ACB,
∴∠ABD+∠ACD=160°×false=20°,
∴∠BCD+∠CBD=140°
∴∠BDC=180﹣∠BCD﹣∠CBD=40°
故答案为40°.
【点睛】
本题考查了三角形内角和定理,角平分线,关键是找出其中的规律,利用规律解决问题.
12.falseβ, falseβ
【解析】
【分析】
已知∠A,求∠A1,利用外角定理可得∠ACD=∠A+∠ABC,∠A1CD=∠A1+∠A1BC,把∠ACD利用角平分线转成2∠A1CD,∠ABC转成2∠A1BC,消去∠A1BC,∠A1CD即可,再用类似的办法求∠A2,以此类推即可
【详解】
∵BA1平分∠ABC,CA1平分∠A1CD,
∴∠AB A1=∠A1BC=false∠ABC,∠AC A1=∠A1CD=false∠ACD,
由三角形的外角得
∴∠A1CD=∠A1+∠A1BC,
∴∠A1CD=∠A1+∠A1BC①
∴2∠A1CD=∠A+2∠A1BC②
把①代入②得∠A1=false∠A=falseβ
CA2平分∠A2CD,
∠A2C A1=∠A2CD=false∠A1CD,
由三角形的外角得
∴∠A1CD=∠A1+∠A1BC,
∴∠A2CD=∠A2+∠A2BC③
∴2∠A2CD=∠A1+2∠A2BC④
解得∠A2=false∠A1,
∠A2=false∠A1false∠A=falseβ=falseβ
同理
∠A3=false∠A2=false∠A=falseβ=falseβ
…
∠A2019= falseβ
故答案为:①falseβ,②falseβ
【点睛】
本题考查(第二内角的)外角平分线与(第一)内角平分线所夹的角问题,找到两平分线的夹角与第三个角的关系是解决问题关键
13.25°
【解析】
【分析】
根据三角形的内角和即可求解.
【详解】
∵在false中,false, false,
∴∠A=180°-∠C-∠B=25°
故答案为:25°.
【点睛】
此题主要考查三角形的角度求解,解题的关键是熟知三角形的内角和为180°.
14.false
【解析】
【分析】
由false、false是false的角平分线,∠BAC=80°,根据三角形内角和定理,可求得false,根据角平分线的定义,可得false,进而解答即可.
【详解】
解:false
false
false、false是false的角平分线,
false,false,
false
false.
故答案为:false.
【点睛】
此题考查了三角形内角和定理以及角平分线的定义.此题难度不大,注意掌握数形结合思想和整体思想的应用.
15.80或100
【解析】
【分析】
根据题意画出图形,当△ABC为锐角三角形或钝角三角形两种情况解答,结合已知条件即可得出∠ABC的度数.
【详解】
(1)如图,当△ABC为锐角三角形时,
∠ACB=∠BCD=80°;
(2)如图,当△ABC为钝角三角形时,
∠ACB=180°-∠BCD=100°.
故答案为:80°或100.
【点睛】
本题考查了三角形内角和定理的应用,关键在于根据题意画出图形,分别进行讨论解答.
16.100或20
【解析】
【分析】
根据BD的不同位置,分两种情况进行讨论:BD在△ABC内部,BD在△ABC外部,分别进行画图计算即可.
【详解】
如图,当BD在△ABC内部时,
∠ABC=∠ABD+∠DBC=90°-∠A +∠DBC=60°+40°=100°;
如图,当BD在△ABC外部时,
∠ABC=∠ABD-∠DBC=90°-∠A -∠DBC =60°-40°=20°;
故答案为:100或20.
【点睛】
本题主要考查了三角形的内角和定理,解决问题的关键是掌握三角形的内角和等于180°,解题时注意分类思想的运用.
17.80°
【解析】
【分析】
三角形内角和是180°,根据三角形内角和定理计算即可.
【详解】
由三角形内角和定理得:
∠C=180°-∠A-∠B=80°,
故答案为80°.
【点睛】
本题考查的是三角形内角和定理的应用,掌握三角形内角和等于180°是解题的关键.
18.50°
【解析】
【分析】
根据平行线的性质求出∠EDF=∠2=40°,根据垂直求出∠FED=90°,根据三角形内角和定理求出即可.
【详解】
解:∵AB∥CD,∠2=40°,
∴∠EDF=∠2=40°,
∵FE⊥DB,
∴∠FED=90°,
∠1=180°-∠FED-∠EDF=180°-90°-40°=50°,
故答案为50°.
【点睛】
本题考查了三角形内角和定理,垂直定义,平行线的性质等知识点,能根据平行线的性质求出∠EDF的度数是解此题的关键.
19.230°
【解析】
【分析】
依据三角形内角和定理,可得△ABC中,∠B+∠C=130°,再根据∠1+∠2+∠B=180°,∠3+∠4+∠C=180°,即可得出∠1+∠2+∠3+∠4=360°﹣(∠B+∠C)=230°.
【详解】
解:∵∠A=50°,
∴△ABC中,∠B+∠C=130°,
又∵∠1+∠2+∠B=180°,∠3+∠4+∠C=180°,
∴∠1+∠2+∠3+∠4=360°﹣(∠B+∠C)=360°﹣130°=230°,
故答案为:230°.
【点睛】
本题主要考查三角形内角和,熟练掌握三角形内角和及角之间的等量关系是解题的关键.
20.false
【解析】
【分析】
根据直角三角板false,false,false,再根据角的和差关系可得false的度数,再利用三角形内角和为false计算出false的度数.
【详解】
解:根据直角三角板false,false,false,
false,
false,
false,
故答案为false.
【点睛】
此题主要考查了三角形内角和定理,以及角的计算,关键是掌握三角形内角和为false,正确计算出false的度数.
21.角平分线定义;false;内错角相等,两直线平行;false;等角的余角相等
【解析】
【分析】
根据垂直的定义可得false,然后根据角平分线定义可得false,根据等量代换可得false∠3,再根据内错角相等,两直线平行可证false,从而得出∠ACB false,再根据等角的余角相等可得false,最后根据对顶角相等和等量代换即可证出结论.
【详解】
证明:false (已知) .
false(垂直的定义).
false平分false (已知)
false(角平分线定义)
false (已知)
false∠3(等量代换)
falsefalse(内错角相等,两直线平行)
false ∠ACB false(两直线平行,内错角相等)
false(直角三角形的两个锐角互余)
同理由false,
可得false
false(等角的余角相等)
又false (对顶角相等 )
false(等量代换)
故答案为: 角平分线定义;false;内错角相等,两直线平行;false;等角的余角相等.
【点睛】
此题考查的是垂直定义、角平分线的定义、直角三角形的性质和平行线的判定及性质,掌握垂直定义、角平分线的定义、直角三角形的性质和平行线的判定及性质是解题关键.
22.∠ECD=17°,∠CDF=73°.
【解析】
【分析】
根据三角形内角和定理求出∠ACB,根据角平分线定义求出∠BCE即可,根据直角三角形两锐角互余求出∠BCD,进而求出∠ECD,再根据直角三角形两锐角互余求出∠CDF即可.
【详解】
解:∵∠A+∠B+∠ACB=180°,∠A=40°,∠B=74°,
∴∠ACB=66°.
∵CE平分∠ACB,
∴∠BCEfalse∠ACBfalse66°=33°.
∵CD⊥AB,
∴∠CDB=90°.
∴∠BCD=90°﹣74°=16°,
∴∠ECD=∠BCE﹣∠BCD=17°.
∵DF⊥CE,
∴∠CFD=90°,
∴∠CDF=90°﹣∠ECD=73°,
即∠ECD=17°,∠CDF=73°.
【点睛】
本题考查了三角形的内角和定理,直角三角形两锐角互余,垂直定义,角平分线定义等知识点,关键是求出各个角的度数.
23.(1)false;(2)false;(3)可以,见解析
【解析】
【分析】
(1)false平分false,可知∠BAE=∠CAE,由三角形内角和可求∠BAC即可,
(2)由AD⊥BC,可求false,由角和差知∠DAE=∠BAE-∠BAD即可,
(3)先求出∠BAC=180゜-∠B-∠C,再求其一半∠BAE,由△ABD,∠BAD=90゜-∠B,作差∠BAE-∠BAD计算即可.
【详解】
解:(1)∵false,
∴false,
∵false平分false
∴false,
(2)∵false于点false,
∴false
∴false,
∴false,
(3)可以.理由如下:
∵false平分false
∴false,
∵false于点false
∴false
∴false,
∴false,
∵false,
∴false.
【点睛】
本题考查角度的规律求法问题,掌握三角形的内角和,角平分线,直角三角形两锐角互余知识是解题关键.
24.20°
【解析】
试题分析:利用三角形外角性质可以得到∠ODB的度数,再利用三角形内角和定理得到∠OAD的度数.
试题解析:
∵∠B=30°,∠E=40°,
∴∠ADO=∠B +∠E =30°+40°=70°,
∵EO⊥CO于点O,
∴∠O=90°,
∴∠OAD=180°-∠O-∠ADO
=180°-90°-70°
=20°.
25.(1)140,90,50;(2)35;(3)false
【解析】
【分析】
(1)根据三角形内角和定理可得∠ABC+∠ACB=180°-∠A=140°,∠DBC+∠DCB=180°-∠DBC=90°,进而可求出∠ABD+∠ACD的度数;
(2)根据三角形内角和定理可得∠ABC+∠ACB=180°-∠A=130°,∠DBC+∠DCB=180°-∠DBC=90°,进而可求出∠ABD+∠ACD的度数;
(3)根据三角形内角和定义有90°+(∠ABD+∠ACD)+∠A=180°,则∠ABD+∠ACD=90°-∠A.
【详解】
解:(1)在△ABC中,∵∠A=40°,
∴∠ABC+∠ACB=180°-40°=140°,
在△DBC中,∵∠BDC=90°,
∴∠DBC+∠DCB=180°-90°=90°,
∴∠ABD+∠ACD=140°-90°=50°;
故答案为:140;90;50.
(2)在△ABC中,∵∠A=55°,
∴∠ABC+∠ACB=180°-55°=125°,
在△DBC中,∵∠BDC=90°,
∴∠DBC+∠DCB=180°-90°=90°,
∴∠ABD+∠ACD=125°-90°=35°,
故答案为:35;
(3)∠ABD+∠ACD与∠A之间的数量关系为:∠ABD+∠ACD=90°-∠A.证明如下:
在△ABC中,∠ABC+∠ACB=180°-∠A.
在△DBC中,∠DBC+∠DCB=90°.
∴∠ABC+∠ACB-(∠DBC+∠DCB)=180°-∠A-90°.
∴∠ABD+∠ACD=90°-∠A,
故答案为:∠ABD+∠ACD=90°-∠A.
【点睛】
本题考查了三角形的内角和定理,熟练掌握三角形的内角和定理是解答的关键.
26.(1)125,90,35;(2)∠ABP+∠ACP=90°-∠A,证明见解析;(3)结论不成立.∠ABP-∠ACP=90°-∠A,∠ABP+∠ACP=∠A-90°或∠ACP - ∠ABP =90°-∠A.
【解析】
【分析】
(1)根据三角形内角和即可得出∠ABC+∠ACB,∠PBC+∠PCB,然后即可得出∠ABP+∠ACP;
(2)根据三角形内角和定理进行等量转换,即可得出∠ABP+∠ACP=90°-∠A;
(3)按照(2)中同样的方法进行等量转换,求解即可判定.
【详解】
(1)∠ABC+∠ACB=180°-∠A=180°-55°=125度,∠PBC+∠PCB=180°-∠P=180°-90°=90度,
∠ABP+∠ACP=∠ABC+∠ACB -(∠PBC+∠PCB)=125°-90°=35度;
(2)猜想:∠ABP+∠ACP=90°-∠A;
证明:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵∠ABC=∠ABP+∠PBC,∠ACB=∠ACP+∠PCB,
∴(∠ABP+∠PBC)+(∠ACP+∠PCB)=180°-∠A,
∴(∠ABP+∠ACP)+(∠PBC+∠PCB)=180°-∠A,
又∵在Rt△PBC中,∠P=90°,
∴∠PBC+∠PCB=90°,
∴(∠ABP+∠ACP)+90°=180°-∠A,
∴∠ABP+∠ACP=90°-∠A.
(3)判断:(2)中的结论不成立.
证明:在△ABC中,∠ABC+∠ACB=180°-∠A,
∵∠ABC=∠PBC-∠ABP,∠ACB=∠PCB-∠ACP,
∴(∠PBC+∠PCB)-(∠ABP+∠ACP)=180°-∠A,
又∵在Rt△PBC中,∠P=90°,
∴∠PBC+∠PCB=90°,
∴∠ABP-∠ACP=90°-∠A,∠ABP+∠ACP=∠A-90°
或∠ACP - ∠ABP =90°-∠A.
【点睛】
此题主要考查利用三角形内角和定理进行等角转换,熟练掌握,即可解题.
27.40;50
【解析】
【分析】
根据三角形内角和定理求解.
【详解】
解:在△ABC中,∠A+∠B+∠C=180°,
∵∠B=40°, ∠C=70°,
∴∠A=180°-∠B-∠C=180°-40°-70°=70°,
∴x=40;
在△ABC中,∠A+∠B+∠C=180°,
∵∠A=80°,
∴80°+x°+x° =180°,
∴x=50.
【点睛】
本题考查三角形的内角和定理,应用内角和定理求角的大小是解答此题的重要途径.
28.83°
【解析】
【分析】
根据对顶角相等,三角形内角和定理解答.
【详解】
解:∵DF⊥AB,
∴∠AFE=90°,
∴∠AEF=90°?∠A=90°?35°=55°,
∴∠CED=∠AEF=55°,
∴∠ACD=180°?∠CED?∠D=180°?55°?42°=83°.
【点睛】
本题考查对顶角的性质,三角形内角和定理:三角形的三个内角和为180°.
29.40°;80°
【解析】
分析:先根据AD是△ABC的高得出∠ADB=90°,再由三角形内角和定理及三角形外角的性质可知∠DBE+∠ADB+∠BED=180°,故∠DBE=180°-∠ADB-∠BED=20°.根据BE平分∠ABC得出∠ABC=2∠DBE=40°.?根据∠BAC+∠ABC+∠C=180°,∠C=60°即可得出结论.
详解:∵AD是△ABC的高,
∴∠ADB=90°.
又∵∠DBE+∠ADB+∠BED=180°,∠BED=70°,
∴∠DBE=180°-∠ADB-∠BED=20°.
∵BE平分∠ABC,
∴∠ABC=2∠DBE=40°.?
又∵∠BAC+∠ABC+∠C=180°,∠C=60°,
∴∠BAC=180°-∠ABC-∠C=80°.
点睛:本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.
30.(1)见解析
(2)135°
【解析】
【分析】
(1)根据直角三角形两锐角互余和角平分线的定义,可以得到角相等,进而得到两边相等;
(2)由三角形的外角性质和内角和定理即可求解.
【详解】
(1)证明:false
又因为BD平分∠ABC,所以false
(2)解:false
