高中数学人教A版必修5第三章3.3.1二元一次不等式与平面区域 课件(14张PPT)
文档属性
| 名称 | 高中数学人教A版必修5第三章3.3.1二元一次不等式与平面区域 课件(14张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-09 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
x
y
o
3.3.1
二元一次不等式(组)与平面区域
会东县和文中学
刘世坤
高2019级7班
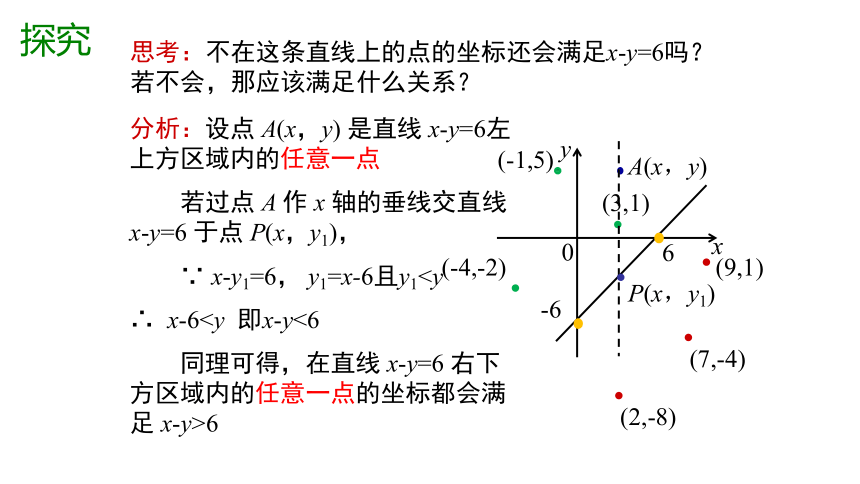
紧扣高考
2020年普通高等学校招生全国统一考试理科数学(三卷)
2020年普通高等学校招生全国统一考试理科数学(一卷)
二元一次不等式(组)的解集与平面区域关系
1.理解二元一次不等式(组)的相关概念;
2.掌握二元一次不等式(组)与平面区域的关系及表示方法;
3.自己能画出二元一次不等式(组)对应的平面区域。
正确画出二元一次不等式(组)对应的平面区域。
【重、难点】
【学习目标】
(1)二元一次不等式:
含有
未知数,并且未知数的最高次数是
的不等式;
(2)二元一次不等式组:
由
二元一次不等式组成的不等式组
(3)二元一次不等式(组)的解集:
满足二元一次不等式(组)的x和y的取值构成
,所有这样的
构成的集合称为二元一次不等式(组)的解集。
二元一次不等式(组)的解集
平面直角坐标系内点构成的集合
两个
1
几个
有序数对(x,y)
有序数对(x,y)
自学导引
x
y
0
-6
6
思考:在直角坐标系内,二元一次不等式(组)的
解集表示什么图形?
如不等式
x-y<6
和x-y>6又表示怎样的图形呢?
x-y=6
思考:在平面直角坐标系内,二元一次方程的解集
表示什么图形?
如方程
x-y=6
表示怎样的图像呢?
分析:设点
A(x,y)
是直线
x-y=6左上方区域内的任意一点
若过点
A
作
x
轴的垂线交直线
x-y=6
于点
P(x,y1),
∵
x-y1=6,
y1=x-6且y1∴
x-6即x-y<6
同理可得,在直线
x-y=6
右下方区域内的任意一点的坐标都会满足
x-y>6
思考:不在这条直线上的点的坐标还会满足x-y=6吗?
若不会,那应该满足什么关系?
x
y
0
-6
6
(3,1)
(-4,-2)
(-1,5)
(2,-8)
(9,1)
(7,-4)
A(x,y)
P(x,y1)
探究
O
x
y
x
–
y
=
6
左上方区域
右下方区域
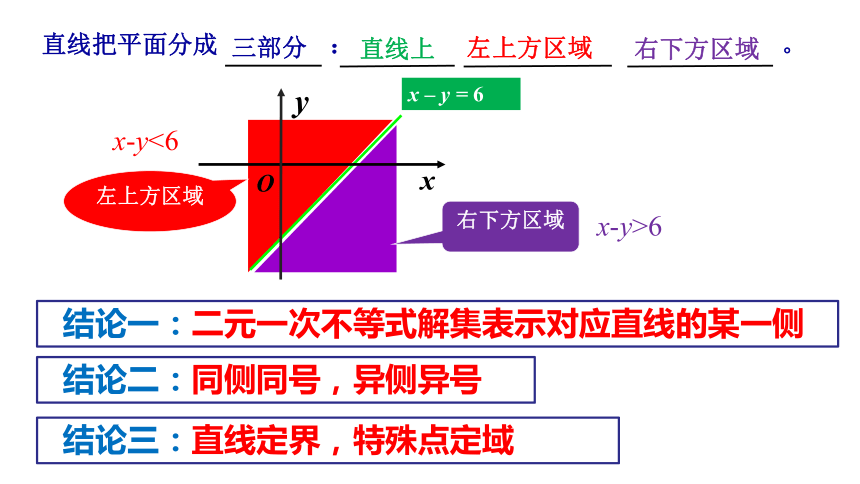
直线把平面分成
:
。
结论二:同侧同号,异侧异号
x-y<6
x-y>6
三部分
直线上
左上方区域
右下方区域
结论一:二元一次不等式解集表示对应直线的某一侧
结论三:直线定界,特殊点定域
例1、画出不等式x+4y<4表示的平面区域。
步骤:
1、先画出对应直线x+4y-4=0.
x
y
o
4
1
又因为这条线上的点都不满足x+4y<4,所以画成虚线.
2、选定一个特殊的点(x0,y0)代入x+4y<4,判断其是否满足,并确定不等式表示的区域.
3、用阴影部分表示不等式的区域.
若直线不经过原点,则常用原点来确定区域
二、例题分析
注意:所画直线一定要在相应的位置标出对应的方程
作图要精准
1、画出下列不等式表示的平面区域:
(1)x-y+1<0;
(2)2x≥
-3y+6
(3)x+y≥0
o
X
Y
-1
O
X
Y
2
学生当堂练习
O
X
Y
(4)x+1<0;
o
X
Y
1
-1
x+1=0
(5)y-2≥0
O
X
Y
3
2
x
y
o
4
8
1612
8
4
解:不等式3x+y-12<0表示
不等式x-2y<0表示
分析:不等式组表示的平面区域是各不等式所表示的平面点集的交集,即各个不等式表示的平面区域的公共部分。
取两区域重叠的部分。
直线3x+y-12=0下方的区域,
直线x-2y=0上方的区域。
二、例题分析
画平面区域的步骤是:
(1)画线:画出不等式所对应的方程所表示的直线(如果原不等式中带等号,则画成实线,否则,画成虚线);
(2)定侧:将某个区域位置明显的一个特殊点的坐标代入不等式,根据“直线定界、特殊点定域”的规律确定不等式所表示的平面区域在直线的哪一侧;常用的特殊点为(0,0)、(±1,0)、(0,±1).
(3)求“交”——如果平面区域是由不等式组决定的,则在确定了各个不等式所表示的区域后,再取这些区域的公共部分,这个公共部分就是不等式组所表示的平面区域.
(4)表示:最后用阴影把公共部分表示出来。
二元一次不等式组表示平面区域的画法(准确作图)
x
y
O
2
4
-2
-4
9
6
3
-3
画出下面的不等式组表示的平面区域
6x+y-6=0
x+y+3=0
学生当堂练习
⑴
二元一次不等式表示平面区域:
直线某一侧所有点组成的平面区域。
⑵
判定方法:
直线定界,特殊点定域,同侧同号,异侧异号。
小结:
⑶
二元一次不等式组表示平面区域:
各个不等式所表示平面区域的公共部分。
知识点
作业:必修五课时作业(99页)
二元一次不等式(组)与平面区域
x
y
o
3.3.1
二元一次不等式(组)与平面区域
会东县和文中学
刘世坤
高2019级7班
紧扣高考
2020年普通高等学校招生全国统一考试理科数学(三卷)
2020年普通高等学校招生全国统一考试理科数学(一卷)
二元一次不等式(组)的解集与平面区域关系
1.理解二元一次不等式(组)的相关概念;
2.掌握二元一次不等式(组)与平面区域的关系及表示方法;
3.自己能画出二元一次不等式(组)对应的平面区域。
正确画出二元一次不等式(组)对应的平面区域。
【重、难点】
【学习目标】
(1)二元一次不等式:
含有
未知数,并且未知数的最高次数是
的不等式;
(2)二元一次不等式组:
由
二元一次不等式组成的不等式组
(3)二元一次不等式(组)的解集:
满足二元一次不等式(组)的x和y的取值构成
,所有这样的
构成的集合称为二元一次不等式(组)的解集。
二元一次不等式(组)的解集
平面直角坐标系内点构成的集合
两个
1
几个
有序数对(x,y)
有序数对(x,y)
自学导引
x
y
0
-6
6
思考:在直角坐标系内,二元一次不等式(组)的
解集表示什么图形?
如不等式
x-y<6
和x-y>6又表示怎样的图形呢?
x-y=6
思考:在平面直角坐标系内,二元一次方程的解集
表示什么图形?
如方程
x-y=6
表示怎样的图像呢?
分析:设点
A(x,y)
是直线
x-y=6左上方区域内的任意一点
若过点
A
作
x
轴的垂线交直线
x-y=6
于点
P(x,y1),
∵
x-y1=6,
y1=x-6且y1
x-6
同理可得,在直线
x-y=6
右下方区域内的任意一点的坐标都会满足
x-y>6
思考:不在这条直线上的点的坐标还会满足x-y=6吗?
若不会,那应该满足什么关系?
x
y
0
-6
6
(3,1)
(-4,-2)
(-1,5)
(2,-8)
(9,1)
(7,-4)
A(x,y)
P(x,y1)
探究
O
x
y
x
–
y
=
6
左上方区域
右下方区域
直线把平面分成
:
。
结论二:同侧同号,异侧异号
x-y<6
x-y>6
三部分
直线上
左上方区域
右下方区域
结论一:二元一次不等式解集表示对应直线的某一侧
结论三:直线定界,特殊点定域
例1、画出不等式x+4y<4表示的平面区域。
步骤:
1、先画出对应直线x+4y-4=0.
x
y
o
4
1
又因为这条线上的点都不满足x+4y<4,所以画成虚线.
2、选定一个特殊的点(x0,y0)代入x+4y<4,判断其是否满足,并确定不等式表示的区域.
3、用阴影部分表示不等式的区域.
若直线不经过原点,则常用原点来确定区域
二、例题分析
注意:所画直线一定要在相应的位置标出对应的方程
作图要精准
1、画出下列不等式表示的平面区域:
(1)x-y+1<0;
(2)2x≥
-3y+6
(3)x+y≥0
o
X
Y
-1
O
X
Y
2
学生当堂练习
O
X
Y
(4)x+1<0;
o
X
Y
1
-1
x+1=0
(5)y-2≥0
O
X
Y
3
2
x
y
o
4
8
1612
8
4
解:不等式3x+y-12<0表示
不等式x-2y<0表示
分析:不等式组表示的平面区域是各不等式所表示的平面点集的交集,即各个不等式表示的平面区域的公共部分。
取两区域重叠的部分。
直线3x+y-12=0下方的区域,
直线x-2y=0上方的区域。
二、例题分析
画平面区域的步骤是:
(1)画线:画出不等式所对应的方程所表示的直线(如果原不等式中带等号,则画成实线,否则,画成虚线);
(2)定侧:将某个区域位置明显的一个特殊点的坐标代入不等式,根据“直线定界、特殊点定域”的规律确定不等式所表示的平面区域在直线的哪一侧;常用的特殊点为(0,0)、(±1,0)、(0,±1).
(3)求“交”——如果平面区域是由不等式组决定的,则在确定了各个不等式所表示的区域后,再取这些区域的公共部分,这个公共部分就是不等式组所表示的平面区域.
(4)表示:最后用阴影把公共部分表示出来。
二元一次不等式组表示平面区域的画法(准确作图)
x
y
O
2
4
-2
-4
9
6
3
-3
画出下面的不等式组表示的平面区域
6x+y-6=0
x+y+3=0
学生当堂练习
⑴
二元一次不等式表示平面区域:
直线某一侧所有点组成的平面区域。
⑵
判定方法:
直线定界,特殊点定域,同侧同号,异侧异号。
小结:
⑶
二元一次不等式组表示平面区域:
各个不等式所表示平面区域的公共部分。
知识点
作业:必修五课时作业(99页)
二元一次不等式(组)与平面区域
