2020-2021学年度人教版七年级数学上册 2.1 整式课时练习(含解析)
文档属性
| 名称 | 2020-2021学年度人教版七年级数学上册 2.1 整式课时练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 562.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 21:03:25 | ||
图片预览




文档简介
2020-2021学年度人教版七年级数学上册2.1整式课时练习
一、选择题
1.用相同大小的等边三角形纸片玩叠纸游戏,可将纸片按如图所示的规律叠放,其中第①个图案有3个60°的角,第②个图案有7个60°的角,第③个图案有10个60°的角,第④个图案有14个60°的角,…,按此规律排列下去,则第⑦个图案中60°的角的个数为( ).
A.21 B.24 C.28 D.31
2.如图,图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,按此规律,则第(n)个图形中面积为1的正方形的个数为( )
A.false B.false C.false D.false
3.代数式 0,false,false,false,false,false,false,false中,多项式有( )
A.1个 B.2个 C.3个 D.4个
4.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,用你所发现的规律得出22017+22018的末位数字是( )
A.2 B.4 C.8 D.6
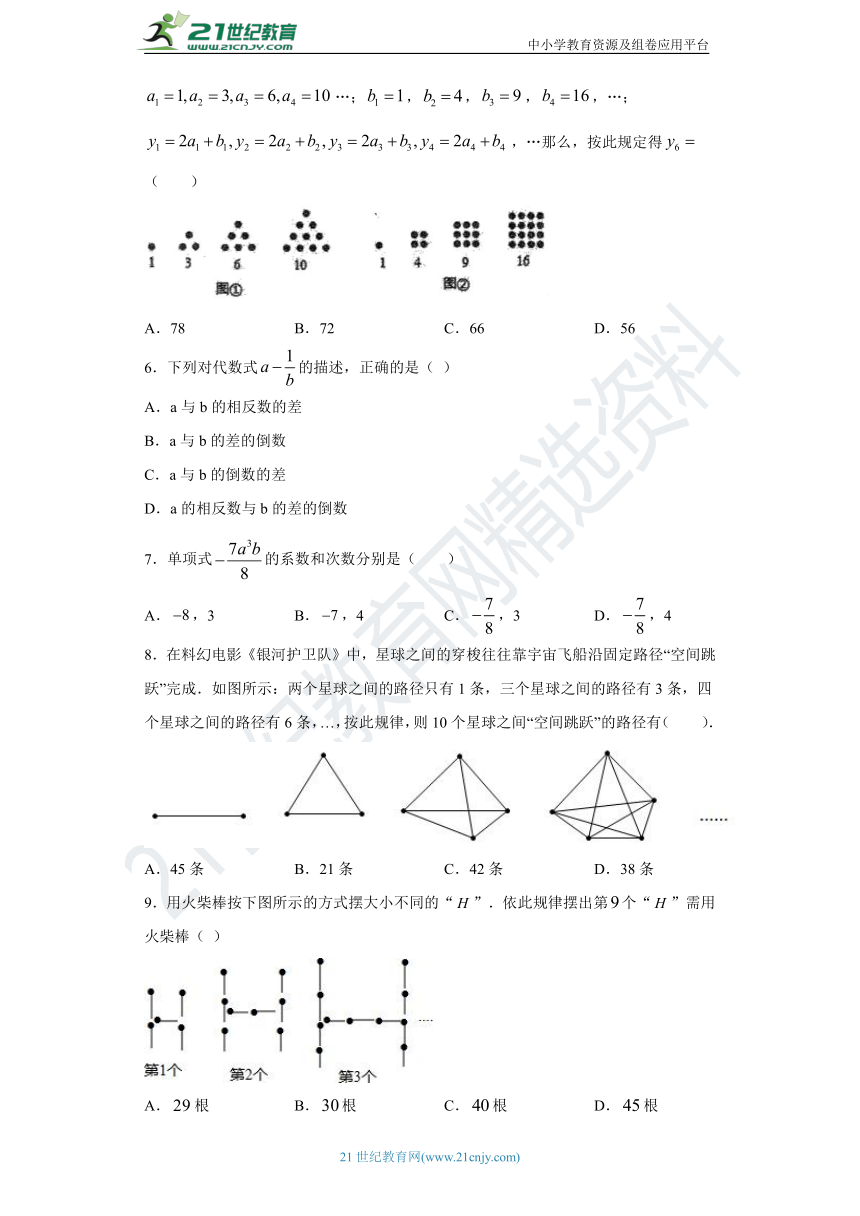
5.古希腊著名的毕达哥拉斯学派把1,3, 6,10,…这样的数称为 “三角形数”(如图①),而把1, 4, 9, 16, ..这样的数称为“正方形数”(如图②).如果规定false…;false,false,false,false,…;false,…那么,按此规定得false( )
A.78 B.72 C.66 D.56
6.下列对代数式false的描述,正确的是( )
A.a与b的相反数的差
B.a与b的差的倒数
C.a与b的倒数的差
D.a的相反数与b的差的倒数
7.单项式false的系数和次数分别是( )
A.false,3 B.false,4 C.false,3 D.false,4
8.在料幻电影《银河护卫队》中,星球之间的穿梭往往靠宇宙飞船沿固定路径“空间跳跃”完成.如图所示:两个星球之间的路径只有1条,三个星球之间的路径有3条,四个星球之间的路径有6条,…,按此规律,则10个星球之间“空间跳跃”的路径有( ).
A.45条 B.21条 C.42条 D.38条
9.用火柴棒按下图所示的方式摆大小不同的“false”.依此规律摆出第false个“false”需用火柴棒( )
A.false根 B.false根 C.false根 D.false根
10.下列整式中,单项式是( )
A.false B.false C.false D.false
二、填空题
11.如图所示,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下图:
则第n个图形中需用黑色瓷砖______________________块(用含n的代数式表示).
12.把多项式false按字母false的降幂排列是______.
13.单项式false的系数是____________,次数是_________.
14.用代数式表示:false与false的差的平方__________.
15.观察算式:false;false;false;false;false;false;…….则false的个位数字是_____.
16.把所有的正整数按如图所示的规律排成数表,若正整数8对应的位置记为false,则false对应的正整数是______.
第1列
第2列
第3列
第4列
第1行
1
2
5
10
第2行
4
3
6
11
第3行
9
8
7
12
第4行
16
15
14
13
17.如果两个关于false的多项式false与false相等,则false___.
18.单项式false的次数是____.
19.1885年瑞士中学数学老师巴尔末(J.J.Balmer)成功地从光谱数据false,false,false,false中得到巴尔末公式,从而打开了光谱奥妙的大门,请你按这种规律写出第false个数据__________.
20.代数式false的系数是________,次数是________.
三、解答题
21.一个多位数false乘11,得到一个新的数,我们把新数去掉首位和末位上的数字剩下的数叫做这个多位数N的“C位数”.如果两个多位数的“C位数”的数字之和相同,我们就称这两个多位数是“黄金搭档”.
例如:∵23×11=253,78×11=858,
∴23和78是黄金搭档,
∵43×11=473,98×11=1078,
∴43和98是黄金搭档.
(1)35的“C位数”是 ,35和99 (是/不是)黄金搭档;
(2)已知一个两位数M,十位数字为a,个位数字为b,满足false,求不大于110的自然数中有多少个数M的“黄金搭档”?
22.观察下列三组数:
第一组:false,false,false,false,false,…;
第二组:1,8,27,64,125,…;
第三组:false,false,false,false,false,….
(1)分别写出三组数中的第7个数.(直接写结果)
(2)取每组数的第10个数,计算这三个数的和.(列式计算)
23.发现:小明经过计算总结出两位数乘11的速算方法:头尾一拉,中间相加,满十进一
例1.计算:false.
方法:32头尾拉开,中间相加,即3+2=5,满十进一,计算结果为352.
例2.计算:false
方法:57头尾拉开,中间相加,即5+7=12,满十进一,计算结果为627
尝试:(1)false .
(2)false .
(3)false .
探究:一个两位数,十位上的数字是m,个位上的数字是n,这个两位数乘11.
(1)若false,计算结果的百位、十位、个位上的数字分别是什么?请通过计算加以证明
(2)若false,直接写出计算结果中十位上的数字.
24.用棋子摆成的“false”字形图如图所示:
(1)填写下表:
图形序号
1
2
3
4
……
15
每个图案中棋子个数
5
8
……
(2)写出第false个“false”字形图案中棋子的个数(用含false的代数式表示)
(3)第30个“false”字形图案共有棋子多少个?
(4)计算出前30个“false”字形图案中棋子的总个数.
25.某销售办公用品的商店推出两种优惠方案:
①购买1个书包,赠送1支水性笔.②书包和水性笔一律按九折优惠.
已知每个书包定价为20元,每支水性笔定价为5元.
(1)小丽和同学需买6个书包,false支水性笔(不少于6支),请用含false的代数式表示两种优惠方案,各需多少元.
(2)若两种方案只能选一种,当false时,采用哪种方案更划算?
26.已知多项式false
(1)把这个多项式按x的降幕重新排列;
(2)请指出该多项式的次数,并写出它的二次项和常数项.
27.已知false、false互为相反数,false、false互为倒数,false的绝对值是false,
求:false的值.
28.观察下列单项式:false,false,false,false,…,false,false,…写出第false个单项式.为解决这个问题,特提供下面的解题思路:通过观察单项式的结构特征,分三步确定:先确定符号,再确定系数的绝对值,最后确定次数.
(1)这组单项式系数的符号规律是________系数的绝对值规律是________;
(2)这组单项式的次数的规律是________;第六个单项式是________;
(3)根据上面的归纳,可以猜想第false个单项式是________;
(4)请你根据猜想,写出第2019个单项式.
29.观察以下等式:
第1个等式:false,
第2个等式:false,
第3个等式:false,
第4个等式:false,
第5个等式:false,
……
按照以上规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第n个等式: (用含n的等式表示)
30.观察下列各式:
false;
false;
false;
false;
......
(1)请写出第5个等式;
(2)利用上述规律,尝试计算false的值.
参考答案
1.B
【解析】
【分析】
观察题目规律,3,7=3+4,10=3+4+3,14=3+4+3+4false依此规律,分n为奇数与n为偶数两种情况讨论.
【详解】
第①个图案有3个60°的角,第②个图案有7个60°的角,第③个图案有10个60°的角,第④个图案有14个60°的角,…,按此规律排列下去,由图可以看出,第n个图案(n为奇数时)是在第n-1个图案上增加了3个60°角;(n为偶数时)是在第n-1个图案上增加了4个60°角,则第⑦个图案中60°的角的个数为3+4+3+4+3+4+3=24(个).
故选:B
【点睛】
本题考查规律型:图形的变化类,是常见考点,难度较易,掌握相关知识是解题关键.
2.C
【解析】
【分析】
由图形可知:第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的图象有2+3=5个,第(3)个图形中面积为1的正方形有2+3+4=9个,…,按此规律,第n个图形中面积为1的正方形有2+3+4+…+n+1=false.
【详解】
第(1)个图形中面积为1的正方形有2个,
第(2)个图形中面积为1的图象有2+3=5个,
第(3)个图形中面积为1的正方形有2+3+4=9个,
…,
按此规律,
第n个图形中面积为1的正方形有2+3+4+…+(n+1)= false个.
【点睛】
本题考查了规律的知识点,解题的关键是根据图形的变化找出规律.
3.C
【解析】
【分析】
直接利用多项式的定义,几个单项式的和叫做多项式,进而得出答案.
【详解】
解:代数式 0,false,false,false,false,false,false,false中,
多项式有false,false,false,共3个,
故选C.
【点睛】
此题主要考查了多项式的定义,正确把握多项式定义是解题关键.
4.D
【解析】
【分析】
因为21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,观察发现:2n的个位数字是2,4,8,6四个一循环,所以根据2017÷4=504…1,2018÷4=504…2,得出22017的个位数字与21的个位数字相同是2,22018的个位数字与22的个位数字相同是4,进一步求解即可.
【详解】
解:∵21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,….
2017÷4=504…1,
2018÷4=504…2,
∴22017的个位数字与21的个位数字相同是2,
22018的个位数字与22的个位数字相同是4,
2+4=6.
故22017+22018的末位数字是6.
故选:D.
【点睛】
本题考查了尾数特征的应用,关键是能根据题意得出规律,利用规律解决问题.
5.A
【解析】
【分析】
根据题中给出的数据可得a6=1+2+3+…+6,b6=62,把相关数值代入y6的代数式计算即可.
【详解】
∵a1=1,a2=1+2=3,a3=1+2+3=6,a4=1+2+3+4=10,…;
b1=12,b2=22=4,b3=32=9,b4=42=16,
∴a6=1+2+3+…+6,b6=62,
∴y6=2a6+b6=2×21+36=78.
故选:A.
【点睛】
本题考查图形的变化规律,根据题意得出得到an,bn的计算方法是解决本题的关键.
6.C
【解析】
【分析】
根据代数式的意义逐项判断即可.
【详解】
解:A. a与b的相反数的差:false,该选项错误;
B. a与b的差的倒数:false,该选项错误;
C. a与b的倒数的差:false;该选项正确;
D. a的相反数与b的差的倒数:false,该选项错误.
故选:C.
【点睛】
此题主要考查列代数式,注意掌握代数式的意义.
7.D
【解析】
【分析】
单项式中的数字因数是单项式的系数,单项式中所有的字母的指数和是单项式的次数,由概念可得答案.
【详解】
解:false的系数是false 次数是false
故选D.
【点睛】
本题考查的是单项式的系数与次数,掌握单项式的系数与次数的含义是解题的关键.
8.A
【解析】
【分析】
观察图形可知,两个星球之间,它们的路径只有1条;三个星球之间的路径有2+1=3条,四个星球之间路径有3+2+1=6条,…,按此规律,可得10个星球之间“空间跳跃”的路径的条数.
【详解】
解:由图形可知,
两个星球之间,它们的路径只有1条;
三个星球之间的路径有2+1=3条,
四个星球之间路径有3+2+1=6条,
……,
按此规律,10个星球之间“空间跳跃”的路径有9+8+7+6+5+4+3+2+1=45条.
故选:A.
【点睛】
本题是图形类规律探求问题,探寻规律时要认真观察、仔细思考,善用联想来解决这类问题.
9.A
【解析】
【分析】
由图可知,第一个“H”用5根火柴,后一个“H”始终比前一个“H”多用3根火.
【详解】
由图可知,第一个“H”用5根火柴,第二个“H”比第一个“H”多用3根火柴,第三个“H”比第二个“H”多用3根火柴,…,以此类推,后一个“H”始终比前一个“H”多用3根火柴,所以,第九个“H”需用火柴:5+3×(9-1)=29根.
故选:A.
【点睛】
本题主要考查规律探索,解题的关键是解读题意并根据图形找出其中的规律.
10.C
【解析】
【分析】
数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式,结合选项即可得出答案.
【详解】
A、不符合单项式的定义,不是单项式,故A选项错误;
B、不符合单项式的定义,不是单项式,故B选项错误;
C、符合单项式的定义,是单项式,故C选项正确;
D、不符合单项式的定义,不是单项式,故D选项错误;
故选:C.
【点睛】
此题考查了单项式的定义,属于基础题,解答本题的关键是掌握单项式的定义.
11.4n+8
【解析】
【分析】
分别清点题目给出的三个图形中的白瓷砖和黑瓷砖的块数,然后通过分析,找出白瓷砖和黑瓷砖的块数与图形数之间的规律,即可解答此题.
【详解】
解:第1个图中有黑色瓷砖的块数为:4×1+8=12块;
第2个图中有黑色瓷砖的块数为:4×2+8=16块;
第3个图中有黑色瓷砖的块数为:4×3+8=20块;
…在第n个图形中有黑色瓷砖的块数为:4n+8.
故答案为:4n+8.
【点睛】
本题考查了图形规律,在处理这类问题时,我们要注意:从具体的、个别的情况分析起,从中进行归纳.
12.false
【解析】
【分析】
先分清各项,然后按降幂排列的定义解答.
【详解】
解:多项式false的各项是false,false,false,false
按x降幂排列为false
故答案为:false.
【点睛】
此题考查的多项式的次数排列,本题降幂排即从x的最高次幂排到最低次幂.
13.false 5
【解析】
【分析】
根据单项式的系数和次数的定义得出即可.
【详解】
解:false?的系数是?false,次数是5,
故答案为:false,5.
【点睛】
本题考查了单项式的系数和次数,能熟记定义的内容是解此题的关键,单项式的数字因数,叫单项式的系数,单项式中所有字母的指数的和,叫单项式的次数.
14.false
【解析】
【分析】
根据a、b的关系分别列式即可
【详解】
解:false与false的差的平方为(a-b)2.
故答案为false.
【点睛】
本题考查了列代数式,是基础题,读懂题目信息,准确把文字语言转化为数学语言是解题的关键.
15.6.
【解析】
【分析】
首先找出31,32,33,34,35,36?32019的末位数字的规律,再求出32019+2019的末位数字即可.
【详解】
∵31=3,32=9,33=27,34=81,35=243,36=729?
∴末位数字分别是3,9,7,1,每四组一个循环,
∵2019÷4=504?3,
∴32019的末位数字是7,
因此,32019+2019的末位数字是6.
故答案为6.
【点睛】
本题考查了数学的变化规律,知道末位数字每四组一循环是解题的关键.
16.75
【解析】
【分析】
先观察出求false对应的数为第9行第7列的数,然后发现第n行第n列的数为n2-(n-1),则可先求得第9行第9列的数,然后可以发现,再同一行中在对角线的左侧,每靠近左侧一列比原数大1即可解答.
【详解】
解:观察可得false对应的数为第9行第7列的数
又观察发现第n行第n列的数为n2-(n-1),则第9行第9列的数为92-(9-1)=73
再观察法则再同一行中在对角线的左侧,每靠近左侧一列比原数大1
则第9行第7列的数73+2=75.
故答案为75.
【点睛】
本题考查了数字类规律,通过观察法则数字的排布规律是解答本题的关键.
17.10
【解析】
【分析】
将两个多项式的各项系数进行比较,即可得a、b、c的值.
【详解】
由题意得:false=false,
∴a=4,b=-2,c=-3,
∴a+bc=4+6=10,
故答案为:10.
【点睛】
此题主要考查了整式的加减??化简求值,关键是正确把式子进行化简.
18.3
【解析】
【分析】
单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.
【详解】
单项式false的次数是:2+1=3,
故填:3.
【点睛】
本题考查了单项式次数的定义,确定单项式的次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式次数的关键.
19.false
【解析】
【分析】
由前四个数可知,分子是序数与2和的平方,分母比分子小4,可得第n个数据.
【详解】
解:∵第1个数:false,
第2个数:false,
第3个数:false,
第4个数:false,
…
∴第n个数据是:false,
故答案为:false.
【点睛】
本题主要考查数字的变化规律,解题的切入点在分子这一平方数,据此容易得到第n个数据.
20.false false
【解析】
【分析】
根据单项式的次数、系数的定义解答.
【详解】
代数式false的系数是false,次数是2.
故答案是:false;2
【点睛】
本题考查单项式,解题关键是熟练掌握单项式的定义.
21.(1)8,是;(2)不大于110的自然数中数15的“黄金搭档”有9个
【解析】
【分析】
(1)根据“false位数”的定义即可求得35的“false位数”;再根据黄金搭档的定义即可求解;
(2)先根据false,由整数的性质得到false,false,可得两位数false为15,其“false位数”为6,进一步得到不大于110的自然数中数15的“黄金搭档”.
【详解】
解:(1)35×11=385,
99×11=1089.
故35的“C位数”是8,35和99是黄金搭档;
(2)3a+2b=13(a≤b),
∵a,b都是非负整数,
∴a=1,b=5,
两位数M为15,
15×11=165,“C位数”是6,
不大于110的自然数中数15的“黄金搭档”有24,33,42,51,60,79,88,97,105,一共9个.
【点睛】
本题考查了规律型:数字的变化类,读懂题意弄明白“false位数”和“黄金搭档”的概念是解题的关键.
22.(1)false,false,false;(2)false
【解析】
【分析】
(1)第一组的数是正整数的平方的相反数,第二组的数是正整数的立方,第三组的数是第二组数的false倍的相反数,从而可得每组的第false个数;
(2)由(1)中的规律分别写出第false个数,再把它们相加即可得到答案.
【详解】
解:(1)第一组的数可依次记为:false
所以第false个数为:false
第二组的数可依次记为:false
所以第false个数为:false
第三组的数可依次记为:false
所以第false个数为:false
(2)由(1)得:三组数的第false个数分别为:false
所以:false
【点睛】
本题考查的是探究数字的规律,列代数式,有理数的加减运算,有理数的乘方运算,掌握由具体到一般的探究规律的方法是解题的关键.
23.尝试(1)473;(2)759;(3)-1078;探究(1)m,m+n,n;过程见解析;(2)m+n-10
【解析】
【分析】
尝试:(1)和(2)根据题目中总结的方法进行计算;
(3)得到的结果是负数,方法不变;
探究:(1)先根据上面的规律猜想,再将这个两位数写成false,用整式的运算进行验证;
(2)根据满十进一的规律得到结果.
【详解】
解:尝试:(1)false;
(2)false;
(3)false;
故答案是:473,759,-1078;
探究:(1)m,m+n,n,
这个两位数是false,
false,
若false,
百位、十位、个位上的数字分别是:m,m+n,n,
(2)同上这个两位数是false,
false,
若false,根据满十进一,
false,
结果的十位上的数应该是false.
【点睛】
本题考查运算找规律,解题的关键是能够总结出题目中的运算规律,并用来计算.
24.(1)11,14,47;(2)false;(3)第30个图案需92个棋子;(4)前30个“T”字形图形案中棋子的总个数为1455个
【解析】
【分析】
(1)通过观察已知图形可得:每个图形都比其前一个图形多3枚棋子,得出摆成第③④⑩个图形需要的棋子数;
(2)由(1)得出规律为摆成第n个图形需要(3n+2)个棋子;
(3)将n=30代入(2)中规律计算即可求解;
(4)由(2)中规律求解即可.
【详解】
(1)首先观察图形,得到前面三个图形的具体个数,发现:在5的基础上依次多3枚.
那么当n=3时,则有11枚;当n=4时,则有14枚;当n=15时,则有47枚;
填表如下:
图形序号
1
2
2
4
…
15
每个图案中棋子个数
5
8
11
14
…
47
故答案为:11,14,47;
(2)因为第①个图案有5枚棋子,
第②个图案有(5+3×1)枚棋子,
第③个图案有(5+3×2)枚棋子,
依此规律可得第n个图案需false枚棋子;
(3)第30个“T”字形图案共有棋子3×30+2=92(个).
即第30个图案需92个棋子;
(4)前30个“T”字形图案中棋子的总个数为:
falsefalsefalse1455(个).
故前30个“T”字形图形案中棋子的总个数为1455个.
【点睛】
本题考查了图形的变化规律,找出图形之间的联系,得出数字的运算规律,利用规律解决问题.
25.(1)方案①需(false)元, 方案②需(false)元;(2)采用方案①更划算
【解析】
【分析】
(1)根据两种优惠方案列式子即可;
(2)将x=32分别代入(1)中的两个式子中,比较大小即可.
【详解】
(1)购1个书包,赠送1支水性笔,
方案①:买6个书包,由此得到还要买(false)支水性笔,
所以得到false;
方案②:购书包和水性笔一律按9折优惠,
所以得到false;
答:按方案①需(false)元, 按方案②需(false)元;
(2)当false时,
方案①:false(元),
方案②:false(元),
∵false,
故采用方案①更划算.
【点睛】
本题考查了列代数式和求代数式的值,搞清数量之间的关系是解题的关键.
26.(1)false;(2)5,xy,false
【解析】
【分析】
(1)按false的降幂排列:即按照false的指数由高到低进行排列即可得到答案;
(2)由多项式中的最高次项的次数是多项式的次数,结合二次项及常数项的概念可得答案.
【详解】
解:(1)按x的降幂排列是:false
(2)由最高次项为:false,所以多项式的次数是5,
它的二次项是xy,常数项是false.
【点睛】
本题考查的是多项式的降幂排列,多项式的二次项,常数项,掌握以上知识是解题的关键.
27.false.
【解析】
【分析】
由相反数,倒数,绝对值的含义求解false的值,再整体代入即可得到答案.
【详解】
解:false false、false互为相反数,
false false,
false false、false互为倒数,
false false,
false false的绝对值是false,
false false,false
false.
【点睛】
本题考查的是相反数,倒数,绝对值的含义,代数式的求值,掌握以上知识及整体代入求代数式的值是解题的关键.
28.(1)(-1)n,2n-1;(2)从1开始的连续自然数,11x6;(3)(-1)n(2n-1)xn;(4)-4037x2019
【解析】
【分析】
(1)根据已知数据得出单项式的系数的符号规律和系数的绝对值规律;
(2)根据已知数据次数得出变化规律;
(3)根据(1)(2)中数据规律得出即可;
(4)利用(3)中所求即可得出答案.
【详解】
解:(1)根据各项系数的符号以及系数的值得出:
这组单项式的系数的符号规律是(-1)n,系数的绝对值规律是2n-1.
故答案为:(-1)n,2n-1;
(2)这组单项式的次数的规律是从1开始的连续自然数.第6个单项式为:11x6
故答案为:从1开始的连续自然数,11x6.
(3)第n个单项式是:(-1)n(2n-1)xn.
故答案为:(-1)n(2n-1)xn;
(4)第2019个单项式是-4037x2019.
故答案为:-4037x2019.
【点睛】
此题主要考查了单项式变化规律,得出次数与系数的变化规律是解题关键.
29.(1)false;(2)false
【解析】
【分析】
(1)根据题目已知给出的式子的规律解答即可;
(2)第n个等式的左边第一项的分母是n,分子是1;第二项的分母是(n+1),分子是(n-1);第三项的第一个式子同第一项,第二个式子同第二项;等式的右边是1,据此解答即可.
【详解】
解:(1)第6个等式为:false;
故答案为:false;
(2)第n个等式为:false;
故答案为:false.
【点睛】
本题考查了数字类规律探索,属于常考题型,找准规律、正确用含n的代数式表示每一项是解题的关键.
30.(1)false;(2)6084
【解析】
【分析】
(1)观察图形可知等式左边各项幂的底数和等于右边幂的底数;
(2)根据(1)的规律即可求解,等式右侧的底数为false.
【详解】
(1)因为false;false;false;
false;
所以false,
即第5个等式为false
(2)由(1)中规律可得,false
【点睛】
本题考查了有理数的乘方运算,此题的关键是找规律,本题的规律为等式左边各项幂的底数和等于右边幂的底数.
一、选择题
1.用相同大小的等边三角形纸片玩叠纸游戏,可将纸片按如图所示的规律叠放,其中第①个图案有3个60°的角,第②个图案有7个60°的角,第③个图案有10个60°的角,第④个图案有14个60°的角,…,按此规律排列下去,则第⑦个图案中60°的角的个数为( ).
A.21 B.24 C.28 D.31
2.如图,图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,按此规律,则第(n)个图形中面积为1的正方形的个数为( )
A.false B.false C.false D.false
3.代数式 0,false,false,false,false,false,false,false中,多项式有( )
A.1个 B.2个 C.3个 D.4个
4.观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,用你所发现的规律得出22017+22018的末位数字是( )
A.2 B.4 C.8 D.6
5.古希腊著名的毕达哥拉斯学派把1,3, 6,10,…这样的数称为 “三角形数”(如图①),而把1, 4, 9, 16, ..这样的数称为“正方形数”(如图②).如果规定false…;false,false,false,false,…;false,…那么,按此规定得false( )
A.78 B.72 C.66 D.56
6.下列对代数式false的描述,正确的是( )
A.a与b的相反数的差
B.a与b的差的倒数
C.a与b的倒数的差
D.a的相反数与b的差的倒数
7.单项式false的系数和次数分别是( )
A.false,3 B.false,4 C.false,3 D.false,4
8.在料幻电影《银河护卫队》中,星球之间的穿梭往往靠宇宙飞船沿固定路径“空间跳跃”完成.如图所示:两个星球之间的路径只有1条,三个星球之间的路径有3条,四个星球之间的路径有6条,…,按此规律,则10个星球之间“空间跳跃”的路径有( ).
A.45条 B.21条 C.42条 D.38条
9.用火柴棒按下图所示的方式摆大小不同的“false”.依此规律摆出第false个“false”需用火柴棒( )
A.false根 B.false根 C.false根 D.false根
10.下列整式中,单项式是( )
A.false B.false C.false D.false
二、填空题
11.如图所示,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下图:
则第n个图形中需用黑色瓷砖______________________块(用含n的代数式表示).
12.把多项式false按字母false的降幂排列是______.
13.单项式false的系数是____________,次数是_________.
14.用代数式表示:false与false的差的平方__________.
15.观察算式:false;false;false;false;false;false;…….则false的个位数字是_____.
16.把所有的正整数按如图所示的规律排成数表,若正整数8对应的位置记为false,则false对应的正整数是______.
第1列
第2列
第3列
第4列
第1行
1
2
5
10
第2行
4
3
6
11
第3行
9
8
7
12
第4行
16
15
14
13
17.如果两个关于false的多项式false与false相等,则false___.
18.单项式false的次数是____.
19.1885年瑞士中学数学老师巴尔末(J.J.Balmer)成功地从光谱数据false,false,false,false中得到巴尔末公式,从而打开了光谱奥妙的大门,请你按这种规律写出第false个数据__________.
20.代数式false的系数是________,次数是________.
三、解答题
21.一个多位数false乘11,得到一个新的数,我们把新数去掉首位和末位上的数字剩下的数叫做这个多位数N的“C位数”.如果两个多位数的“C位数”的数字之和相同,我们就称这两个多位数是“黄金搭档”.
例如:∵23×11=253,78×11=858,
∴23和78是黄金搭档,
∵43×11=473,98×11=1078,
∴43和98是黄金搭档.
(1)35的“C位数”是 ,35和99 (是/不是)黄金搭档;
(2)已知一个两位数M,十位数字为a,个位数字为b,满足false,求不大于110的自然数中有多少个数M的“黄金搭档”?
22.观察下列三组数:
第一组:false,false,false,false,false,…;
第二组:1,8,27,64,125,…;
第三组:false,false,false,false,false,….
(1)分别写出三组数中的第7个数.(直接写结果)
(2)取每组数的第10个数,计算这三个数的和.(列式计算)
23.发现:小明经过计算总结出两位数乘11的速算方法:头尾一拉,中间相加,满十进一
例1.计算:false.
方法:32头尾拉开,中间相加,即3+2=5,满十进一,计算结果为352.
例2.计算:false
方法:57头尾拉开,中间相加,即5+7=12,满十进一,计算结果为627
尝试:(1)false .
(2)false .
(3)false .
探究:一个两位数,十位上的数字是m,个位上的数字是n,这个两位数乘11.
(1)若false,计算结果的百位、十位、个位上的数字分别是什么?请通过计算加以证明
(2)若false,直接写出计算结果中十位上的数字.
24.用棋子摆成的“false”字形图如图所示:
(1)填写下表:
图形序号
1
2
3
4
……
15
每个图案中棋子个数
5
8
……
(2)写出第false个“false”字形图案中棋子的个数(用含false的代数式表示)
(3)第30个“false”字形图案共有棋子多少个?
(4)计算出前30个“false”字形图案中棋子的总个数.
25.某销售办公用品的商店推出两种优惠方案:
①购买1个书包,赠送1支水性笔.②书包和水性笔一律按九折优惠.
已知每个书包定价为20元,每支水性笔定价为5元.
(1)小丽和同学需买6个书包,false支水性笔(不少于6支),请用含false的代数式表示两种优惠方案,各需多少元.
(2)若两种方案只能选一种,当false时,采用哪种方案更划算?
26.已知多项式false
(1)把这个多项式按x的降幕重新排列;
(2)请指出该多项式的次数,并写出它的二次项和常数项.
27.已知false、false互为相反数,false、false互为倒数,false的绝对值是false,
求:false的值.
28.观察下列单项式:false,false,false,false,…,false,false,…写出第false个单项式.为解决这个问题,特提供下面的解题思路:通过观察单项式的结构特征,分三步确定:先确定符号,再确定系数的绝对值,最后确定次数.
(1)这组单项式系数的符号规律是________系数的绝对值规律是________;
(2)这组单项式的次数的规律是________;第六个单项式是________;
(3)根据上面的归纳,可以猜想第false个单项式是________;
(4)请你根据猜想,写出第2019个单项式.
29.观察以下等式:
第1个等式:false,
第2个等式:false,
第3个等式:false,
第4个等式:false,
第5个等式:false,
……
按照以上规律,解决下列问题:
(1)写出第6个等式: ;
(2)写出你猜想的第n个等式: (用含n的等式表示)
30.观察下列各式:
false;
false;
false;
false;
......
(1)请写出第5个等式;
(2)利用上述规律,尝试计算false的值.
参考答案
1.B
【解析】
【分析】
观察题目规律,3,7=3+4,10=3+4+3,14=3+4+3+4false依此规律,分n为奇数与n为偶数两种情况讨论.
【详解】
第①个图案有3个60°的角,第②个图案有7个60°的角,第③个图案有10个60°的角,第④个图案有14个60°的角,…,按此规律排列下去,由图可以看出,第n个图案(n为奇数时)是在第n-1个图案上增加了3个60°角;(n为偶数时)是在第n-1个图案上增加了4个60°角,则第⑦个图案中60°的角的个数为3+4+3+4+3+4+3=24(个).
故选:B
【点睛】
本题考查规律型:图形的变化类,是常见考点,难度较易,掌握相关知识是解题关键.
2.C
【解析】
【分析】
由图形可知:第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的图象有2+3=5个,第(3)个图形中面积为1的正方形有2+3+4=9个,…,按此规律,第n个图形中面积为1的正方形有2+3+4+…+n+1=false.
【详解】
第(1)个图形中面积为1的正方形有2个,
第(2)个图形中面积为1的图象有2+3=5个,
第(3)个图形中面积为1的正方形有2+3+4=9个,
…,
按此规律,
第n个图形中面积为1的正方形有2+3+4+…+(n+1)= false个.
【点睛】
本题考查了规律的知识点,解题的关键是根据图形的变化找出规律.
3.C
【解析】
【分析】
直接利用多项式的定义,几个单项式的和叫做多项式,进而得出答案.
【详解】
解:代数式 0,false,false,false,false,false,false,false中,
多项式有false,false,false,共3个,
故选C.
【点睛】
此题主要考查了多项式的定义,正确把握多项式定义是解题关键.
4.D
【解析】
【分析】
因为21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,观察发现:2n的个位数字是2,4,8,6四个一循环,所以根据2017÷4=504…1,2018÷4=504…2,得出22017的个位数字与21的个位数字相同是2,22018的个位数字与22的个位数字相同是4,进一步求解即可.
【详解】
解:∵21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,….
2017÷4=504…1,
2018÷4=504…2,
∴22017的个位数字与21的个位数字相同是2,
22018的个位数字与22的个位数字相同是4,
2+4=6.
故22017+22018的末位数字是6.
故选:D.
【点睛】
本题考查了尾数特征的应用,关键是能根据题意得出规律,利用规律解决问题.
5.A
【解析】
【分析】
根据题中给出的数据可得a6=1+2+3+…+6,b6=62,把相关数值代入y6的代数式计算即可.
【详解】
∵a1=1,a2=1+2=3,a3=1+2+3=6,a4=1+2+3+4=10,…;
b1=12,b2=22=4,b3=32=9,b4=42=16,
∴a6=1+2+3+…+6,b6=62,
∴y6=2a6+b6=2×21+36=78.
故选:A.
【点睛】
本题考查图形的变化规律,根据题意得出得到an,bn的计算方法是解决本题的关键.
6.C
【解析】
【分析】
根据代数式的意义逐项判断即可.
【详解】
解:A. a与b的相反数的差:false,该选项错误;
B. a与b的差的倒数:false,该选项错误;
C. a与b的倒数的差:false;该选项正确;
D. a的相反数与b的差的倒数:false,该选项错误.
故选:C.
【点睛】
此题主要考查列代数式,注意掌握代数式的意义.
7.D
【解析】
【分析】
单项式中的数字因数是单项式的系数,单项式中所有的字母的指数和是单项式的次数,由概念可得答案.
【详解】
解:false的系数是false 次数是false
故选D.
【点睛】
本题考查的是单项式的系数与次数,掌握单项式的系数与次数的含义是解题的关键.
8.A
【解析】
【分析】
观察图形可知,两个星球之间,它们的路径只有1条;三个星球之间的路径有2+1=3条,四个星球之间路径有3+2+1=6条,…,按此规律,可得10个星球之间“空间跳跃”的路径的条数.
【详解】
解:由图形可知,
两个星球之间,它们的路径只有1条;
三个星球之间的路径有2+1=3条,
四个星球之间路径有3+2+1=6条,
……,
按此规律,10个星球之间“空间跳跃”的路径有9+8+7+6+5+4+3+2+1=45条.
故选:A.
【点睛】
本题是图形类规律探求问题,探寻规律时要认真观察、仔细思考,善用联想来解决这类问题.
9.A
【解析】
【分析】
由图可知,第一个“H”用5根火柴,后一个“H”始终比前一个“H”多用3根火.
【详解】
由图可知,第一个“H”用5根火柴,第二个“H”比第一个“H”多用3根火柴,第三个“H”比第二个“H”多用3根火柴,…,以此类推,后一个“H”始终比前一个“H”多用3根火柴,所以,第九个“H”需用火柴:5+3×(9-1)=29根.
故选:A.
【点睛】
本题主要考查规律探索,解题的关键是解读题意并根据图形找出其中的规律.
10.C
【解析】
【分析】
数或字母的积组成的式子叫做单项式,单独的一个数或字母也是单项式,结合选项即可得出答案.
【详解】
A、不符合单项式的定义,不是单项式,故A选项错误;
B、不符合单项式的定义,不是单项式,故B选项错误;
C、符合单项式的定义,是单项式,故C选项正确;
D、不符合单项式的定义,不是单项式,故D选项错误;
故选:C.
【点睛】
此题考查了单项式的定义,属于基础题,解答本题的关键是掌握单项式的定义.
11.4n+8
【解析】
【分析】
分别清点题目给出的三个图形中的白瓷砖和黑瓷砖的块数,然后通过分析,找出白瓷砖和黑瓷砖的块数与图形数之间的规律,即可解答此题.
【详解】
解:第1个图中有黑色瓷砖的块数为:4×1+8=12块;
第2个图中有黑色瓷砖的块数为:4×2+8=16块;
第3个图中有黑色瓷砖的块数为:4×3+8=20块;
…在第n个图形中有黑色瓷砖的块数为:4n+8.
故答案为:4n+8.
【点睛】
本题考查了图形规律,在处理这类问题时,我们要注意:从具体的、个别的情况分析起,从中进行归纳.
12.false
【解析】
【分析】
先分清各项,然后按降幂排列的定义解答.
【详解】
解:多项式false的各项是false,false,false,false
按x降幂排列为false
故答案为:false.
【点睛】
此题考查的多项式的次数排列,本题降幂排即从x的最高次幂排到最低次幂.
13.false 5
【解析】
【分析】
根据单项式的系数和次数的定义得出即可.
【详解】
解:false?的系数是?false,次数是5,
故答案为:false,5.
【点睛】
本题考查了单项式的系数和次数,能熟记定义的内容是解此题的关键,单项式的数字因数,叫单项式的系数,单项式中所有字母的指数的和,叫单项式的次数.
14.false
【解析】
【分析】
根据a、b的关系分别列式即可
【详解】
解:false与false的差的平方为(a-b)2.
故答案为false.
【点睛】
本题考查了列代数式,是基础题,读懂题目信息,准确把文字语言转化为数学语言是解题的关键.
15.6.
【解析】
【分析】
首先找出31,32,33,34,35,36?32019的末位数字的规律,再求出32019+2019的末位数字即可.
【详解】
∵31=3,32=9,33=27,34=81,35=243,36=729?
∴末位数字分别是3,9,7,1,每四组一个循环,
∵2019÷4=504?3,
∴32019的末位数字是7,
因此,32019+2019的末位数字是6.
故答案为6.
【点睛】
本题考查了数学的变化规律,知道末位数字每四组一循环是解题的关键.
16.75
【解析】
【分析】
先观察出求false对应的数为第9行第7列的数,然后发现第n行第n列的数为n2-(n-1),则可先求得第9行第9列的数,然后可以发现,再同一行中在对角线的左侧,每靠近左侧一列比原数大1即可解答.
【详解】
解:观察可得false对应的数为第9行第7列的数
又观察发现第n行第n列的数为n2-(n-1),则第9行第9列的数为92-(9-1)=73
再观察法则再同一行中在对角线的左侧,每靠近左侧一列比原数大1
则第9行第7列的数73+2=75.
故答案为75.
【点睛】
本题考查了数字类规律,通过观察法则数字的排布规律是解答本题的关键.
17.10
【解析】
【分析】
将两个多项式的各项系数进行比较,即可得a、b、c的值.
【详解】
由题意得:false=false,
∴a=4,b=-2,c=-3,
∴a+bc=4+6=10,
故答案为:10.
【点睛】
此题主要考查了整式的加减??化简求值,关键是正确把式子进行化简.
18.3
【解析】
【分析】
单项式中数字因数叫做单项式的系数,所有字母的指数和叫做这个单项式的次数.
【详解】
单项式false的次数是:2+1=3,
故填:3.
【点睛】
本题考查了单项式次数的定义,确定单项式的次数时,把一个单项式分解成数字因数和字母因式的积,是找准单项式次数的关键.
19.false
【解析】
【分析】
由前四个数可知,分子是序数与2和的平方,分母比分子小4,可得第n个数据.
【详解】
解:∵第1个数:false,
第2个数:false,
第3个数:false,
第4个数:false,
…
∴第n个数据是:false,
故答案为:false.
【点睛】
本题主要考查数字的变化规律,解题的切入点在分子这一平方数,据此容易得到第n个数据.
20.false false
【解析】
【分析】
根据单项式的次数、系数的定义解答.
【详解】
代数式false的系数是false,次数是2.
故答案是:false;2
【点睛】
本题考查单项式,解题关键是熟练掌握单项式的定义.
21.(1)8,是;(2)不大于110的自然数中数15的“黄金搭档”有9个
【解析】
【分析】
(1)根据“false位数”的定义即可求得35的“false位数”;再根据黄金搭档的定义即可求解;
(2)先根据false,由整数的性质得到false,false,可得两位数false为15,其“false位数”为6,进一步得到不大于110的自然数中数15的“黄金搭档”.
【详解】
解:(1)35×11=385,
99×11=1089.
故35的“C位数”是8,35和99是黄金搭档;
(2)3a+2b=13(a≤b),
∵a,b都是非负整数,
∴a=1,b=5,
两位数M为15,
15×11=165,“C位数”是6,
不大于110的自然数中数15的“黄金搭档”有24,33,42,51,60,79,88,97,105,一共9个.
【点睛】
本题考查了规律型:数字的变化类,读懂题意弄明白“false位数”和“黄金搭档”的概念是解题的关键.
22.(1)false,false,false;(2)false
【解析】
【分析】
(1)第一组的数是正整数的平方的相反数,第二组的数是正整数的立方,第三组的数是第二组数的false倍的相反数,从而可得每组的第false个数;
(2)由(1)中的规律分别写出第false个数,再把它们相加即可得到答案.
【详解】
解:(1)第一组的数可依次记为:false
所以第false个数为:false
第二组的数可依次记为:false
所以第false个数为:false
第三组的数可依次记为:false
所以第false个数为:false
(2)由(1)得:三组数的第false个数分别为:false
所以:false
【点睛】
本题考查的是探究数字的规律,列代数式,有理数的加减运算,有理数的乘方运算,掌握由具体到一般的探究规律的方法是解题的关键.
23.尝试(1)473;(2)759;(3)-1078;探究(1)m,m+n,n;过程见解析;(2)m+n-10
【解析】
【分析】
尝试:(1)和(2)根据题目中总结的方法进行计算;
(3)得到的结果是负数,方法不变;
探究:(1)先根据上面的规律猜想,再将这个两位数写成false,用整式的运算进行验证;
(2)根据满十进一的规律得到结果.
【详解】
解:尝试:(1)false;
(2)false;
(3)false;
故答案是:473,759,-1078;
探究:(1)m,m+n,n,
这个两位数是false,
false,
若false,
百位、十位、个位上的数字分别是:m,m+n,n,
(2)同上这个两位数是false,
false,
若false,根据满十进一,
false,
结果的十位上的数应该是false.
【点睛】
本题考查运算找规律,解题的关键是能够总结出题目中的运算规律,并用来计算.
24.(1)11,14,47;(2)false;(3)第30个图案需92个棋子;(4)前30个“T”字形图形案中棋子的总个数为1455个
【解析】
【分析】
(1)通过观察已知图形可得:每个图形都比其前一个图形多3枚棋子,得出摆成第③④⑩个图形需要的棋子数;
(2)由(1)得出规律为摆成第n个图形需要(3n+2)个棋子;
(3)将n=30代入(2)中规律计算即可求解;
(4)由(2)中规律求解即可.
【详解】
(1)首先观察图形,得到前面三个图形的具体个数,发现:在5的基础上依次多3枚.
那么当n=3时,则有11枚;当n=4时,则有14枚;当n=15时,则有47枚;
填表如下:
图形序号
1
2
2
4
…
15
每个图案中棋子个数
5
8
11
14
…
47
故答案为:11,14,47;
(2)因为第①个图案有5枚棋子,
第②个图案有(5+3×1)枚棋子,
第③个图案有(5+3×2)枚棋子,
依此规律可得第n个图案需false枚棋子;
(3)第30个“T”字形图案共有棋子3×30+2=92(个).
即第30个图案需92个棋子;
(4)前30个“T”字形图案中棋子的总个数为:
falsefalsefalse1455(个).
故前30个“T”字形图形案中棋子的总个数为1455个.
【点睛】
本题考查了图形的变化规律,找出图形之间的联系,得出数字的运算规律,利用规律解决问题.
25.(1)方案①需(false)元, 方案②需(false)元;(2)采用方案①更划算
【解析】
【分析】
(1)根据两种优惠方案列式子即可;
(2)将x=32分别代入(1)中的两个式子中,比较大小即可.
【详解】
(1)购1个书包,赠送1支水性笔,
方案①:买6个书包,由此得到还要买(false)支水性笔,
所以得到false;
方案②:购书包和水性笔一律按9折优惠,
所以得到false;
答:按方案①需(false)元, 按方案②需(false)元;
(2)当false时,
方案①:false(元),
方案②:false(元),
∵false,
故采用方案①更划算.
【点睛】
本题考查了列代数式和求代数式的值,搞清数量之间的关系是解题的关键.
26.(1)false;(2)5,xy,false
【解析】
【分析】
(1)按false的降幂排列:即按照false的指数由高到低进行排列即可得到答案;
(2)由多项式中的最高次项的次数是多项式的次数,结合二次项及常数项的概念可得答案.
【详解】
解:(1)按x的降幂排列是:false
(2)由最高次项为:false,所以多项式的次数是5,
它的二次项是xy,常数项是false.
【点睛】
本题考查的是多项式的降幂排列,多项式的二次项,常数项,掌握以上知识是解题的关键.
27.false.
【解析】
【分析】
由相反数,倒数,绝对值的含义求解false的值,再整体代入即可得到答案.
【详解】
解:false false、false互为相反数,
false false,
false false、false互为倒数,
false false,
false false的绝对值是false,
false false,false
false.
【点睛】
本题考查的是相反数,倒数,绝对值的含义,代数式的求值,掌握以上知识及整体代入求代数式的值是解题的关键.
28.(1)(-1)n,2n-1;(2)从1开始的连续自然数,11x6;(3)(-1)n(2n-1)xn;(4)-4037x2019
【解析】
【分析】
(1)根据已知数据得出单项式的系数的符号规律和系数的绝对值规律;
(2)根据已知数据次数得出变化规律;
(3)根据(1)(2)中数据规律得出即可;
(4)利用(3)中所求即可得出答案.
【详解】
解:(1)根据各项系数的符号以及系数的值得出:
这组单项式的系数的符号规律是(-1)n,系数的绝对值规律是2n-1.
故答案为:(-1)n,2n-1;
(2)这组单项式的次数的规律是从1开始的连续自然数.第6个单项式为:11x6
故答案为:从1开始的连续自然数,11x6.
(3)第n个单项式是:(-1)n(2n-1)xn.
故答案为:(-1)n(2n-1)xn;
(4)第2019个单项式是-4037x2019.
故答案为:-4037x2019.
【点睛】
此题主要考查了单项式变化规律,得出次数与系数的变化规律是解题关键.
29.(1)false;(2)false
【解析】
【分析】
(1)根据题目已知给出的式子的规律解答即可;
(2)第n个等式的左边第一项的分母是n,分子是1;第二项的分母是(n+1),分子是(n-1);第三项的第一个式子同第一项,第二个式子同第二项;等式的右边是1,据此解答即可.
【详解】
解:(1)第6个等式为:false;
故答案为:false;
(2)第n个等式为:false;
故答案为:false.
【点睛】
本题考查了数字类规律探索,属于常考题型,找准规律、正确用含n的代数式表示每一项是解题的关键.
30.(1)false;(2)6084
【解析】
【分析】
(1)观察图形可知等式左边各项幂的底数和等于右边幂的底数;
(2)根据(1)的规律即可求解,等式右侧的底数为false.
【详解】
(1)因为false;false;false;
false;
所以false,
即第5个等式为false
(2)由(1)中规律可得,false
【点睛】
本题考查了有理数的乘方运算,此题的关键是找规律,本题的规律为等式左边各项幂的底数和等于右边幂的底数.
