人教版数学九年级上册25.1.1随机事件课件(共24张PPT)
文档属性
| 名称 | 人教版数学九年级上册25.1.1随机事件课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 09:31:36 | ||
图片预览







文档简介
②明天,地球还会转动
③煮熟的鸭子,飞了
④00C以下,这些雪融化
下列现象哪些是必然发生的,哪些是不可能发生的?
①木柴燃烧,产生热量
打开电视正在播刘翔夺冠的体育片
这两人各买1张彩票,她们中奖了
25.1.1随机事件
第二十五章概率初步
学习目标
1、 知道必然事件、不可能事件、随机事件的概念和特点。
2、会根据事件的特点判断一个简单事件是属于必然事件、不可能事件还是随机事件。
3、在解答问题的过程中,体验从事物的表象到本质的探究历程,感受数学的科学性及生活中丰富的数学现象。
在一定条件下:
必然会发生的事件叫必然事件;
必然不会发生的事件叫不可能事件;
可能会发生,也可能不发生的事件叫随机事件.
要记住我哦!
自学交流
(1)抽到的序号有几种可能的结果?
5名同学参加演讲比赛,以抽签方式决定每个人的出场顺序。签筒中有5根形状大小相同的纸签,上面分别标有出场的序号1,2,3,4,5。小军首先抽签,他在看不到的纸签上的数字的情况从签筒中随机(任意)地取一根纸签。
(2)抽到的序号小于6;
(3)抽到的序号是0;
(4)抽到的序号是1;
思考:下列哪些事件是必然事件,
哪些事件是不可能事件?
5种
必然事件
不可能事件
随机事件
认识事件
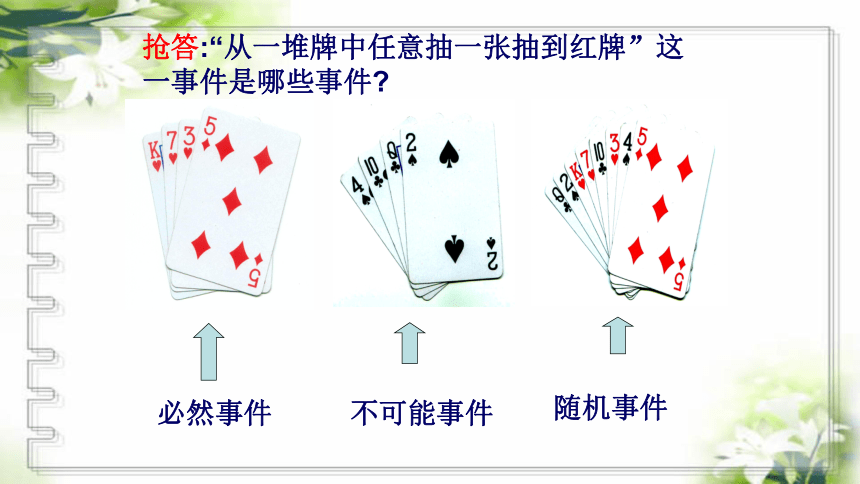
抢答:“从一堆牌中任意抽一张抽到红牌”这一事件是哪些事件?
随机事件
必然事件
不可能事件
三人每次都能摸到红球吗?
②明天,地球还会转动
③煮熟的鸭子,飞了
④00C以下,这些雪融化
下列现象哪些是必然事件,哪些是不可能事件?
①木柴燃烧,产生热量
打开电视正在播刘翔夺冠的体育片
这两人各买1张彩票,她们中奖了
(5)经过城市中某一有交通信号灯的路口,
遇到红灯;
(4)度量三角形的内角和,结果是360°;
(3)掷一枚骰子,向上的一面是6点;
(2)篮球队员在罚线上投篮一次,未投中;
二、下列事件中,哪些是必然发生的,哪些是不可能
发生的,哪些是随机事件。
(1)通常加热到100℃时,水沸腾;
必然事件
随机事件
随机事件
不可能发生
随机事件
世界是你们的,你说我听
(6)汽车累积行驶1万公里,从未出现故障。
随机事件
(7)抛一枚硬币,正面向上。
随机事件
合作交流:
必然事件
不可能事件
不确定事件
事件
确定事件
必然事件、不可能事件、随机事件各有什么特征?
随机事件
⑴度量三角形内角和,结果是360°.
⑵正常情况下水加热到100°C,就会沸腾.
⑶掷一个正面体的骰子,向上一面点数为6.
⑷经过城市中某一有交通信号灯的路口,遇到红灯.
(5)某射击运动员射击一次,命中靶心.
(不可能事件)
(必然事件)
(随机事件)
(随机事件)
(随机事件)
练一练:
指出下列事件中哪些事件是必然事件,哪些事件是不可以事件,哪些事件是随机事件.
牛刀小试
(6)同一枚骰子连续掷两次,朝上一面出现点数之和为14.
(7)任意四边形的内角和都等于360°.
(8)一辆小汽车从面前经过,它的车牌号码为偶数.
(9)从一副完整扑克牌中任抽一张,它是草花.
(必然事件)
(不可能事件)
(随机事件)
(随机事件)
合作交流:
说说你身边的事件,让同桌判断是哪些事件?
1. 指出下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件?
(1)同旁内角互补,两直线平行。 (2)石河子明天下大雨。 (3)1+1=3。
(4)掷一次骰子,向上一面是6点。 (5)11个人中,至少有两个人出生的月份相同。
(6)中国足球队夺得世界杯冠军。 (7)在装有3个红球的布袋里摸出绿球。
(8)对顶角相等。 (9)太阳从西边下山。 (10)数学测试你得满分。
必然事件是 。不可能事件是: 。随机事件是: 。(写出序号即可)
当堂检测:
中考链接:
1. “a是实数,|a|≥0”这一事件是 ( )
A. 必然事件 B. 不确定事件
C. 不可能事件 D. 随机事件
2. 下列说法中正确的是( )
A.“打开电视,正在播放《新闻联播》”是必然事件;
B.某次抽奖活动中奖的机会为1/100,说明每买100张奖券,一定有一次中奖;
C.数据1,1,2,2,3的众数是3;
D.想了解某市城镇居民人均年收入水平,宜采用抽样调查。
3. 下列事件中,是确定事件的是( )
A.打雷后会下雨 B.明天是睛天
C. 1小时等于60分钟 D.下雨后有彩虹
4.下列事件是必然事件的是( )
A.通常加热到100℃,水沸腾;
B.抛一枚硬币,正面朝上;
C.明天会下雨;
D.经过城市中某一有交通信号灯的路口,恰好遇到红灯。
中考链接:
欣赏
学到了什么:
必然发生的事件
不可能发生的事件
随机事件
事件
确定事件
定义:在一定条件下,有可能发生也有可能不发生称为随机事件
特征:事先不能预料即具有不确定性。
课后作业:
必做题:
1、课本:P131习题25.1 第1题
2、预习课本 P127-128的知识
嘿嘿,这次非让你死不可!
生死签的传说
相传古代有个王国,国王非常阴险而多疑,一位正直的大臣得罪了国王,被判死刑。这个国家世代沿袭着一条奇特的法规:凡是死囚,在临刑前都要抽一次“生死签”(写着“生”和“死”的两张纸条),犯人当众抽签,若抽到“死”签,则立即处死,若抽到“生”签,则当场赦免。
国王一心想处死大臣,与几个心腹密谋,想出一条毒计:暗中让执行官把“生死签”上都写成“死”,两死抽一,必死无疑。
然而在断头台前,聪明的大臣迅速抽出一张签纸塞进嘴里,等到执行官反应过来,签纸早已吞下,大臣故作叹息说:“我听天意,将苦果吞下,只要看剩下的签是什么字就清楚了。”剩下的当然写着“死”字,国王怕犯众怒,只好当众释放了大臣。
国王“机关算尽”,想让大臣死,反而搬起石头砸自己脚,让机智的大臣死里逃生。
嘿嘿,这次非让你死不可!
老臣自有妙计!
思考:
(1)在国王的阴谋中,大臣被处死是什么事件?
(2)在大臣的计策中,大臣被处死是什么事件?
一定条件
必然事件
不可能事件
摸球试验:袋中装有4个黄球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球。
(1)这个球是白球还是黄球?
(2)如果两种球都有可能被摸出,那么摸出黄球和摸出白球的可能性一样大吗?
归纳:一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同。
思考:能否通过改变袋子中某种颜色的球的数量,使“摸出黄球”和“摸出白球”的可能性大小相同?
③煮熟的鸭子,飞了
④00C以下,这些雪融化
下列现象哪些是必然发生的,哪些是不可能发生的?
①木柴燃烧,产生热量
打开电视正在播刘翔夺冠的体育片
这两人各买1张彩票,她们中奖了
25.1.1随机事件
第二十五章概率初步
学习目标
1、 知道必然事件、不可能事件、随机事件的概念和特点。
2、会根据事件的特点判断一个简单事件是属于必然事件、不可能事件还是随机事件。
3、在解答问题的过程中,体验从事物的表象到本质的探究历程,感受数学的科学性及生活中丰富的数学现象。
在一定条件下:
必然会发生的事件叫必然事件;
必然不会发生的事件叫不可能事件;
可能会发生,也可能不发生的事件叫随机事件.
要记住我哦!
自学交流
(1)抽到的序号有几种可能的结果?
5名同学参加演讲比赛,以抽签方式决定每个人的出场顺序。签筒中有5根形状大小相同的纸签,上面分别标有出场的序号1,2,3,4,5。小军首先抽签,他在看不到的纸签上的数字的情况从签筒中随机(任意)地取一根纸签。
(2)抽到的序号小于6;
(3)抽到的序号是0;
(4)抽到的序号是1;
思考:下列哪些事件是必然事件,
哪些事件是不可能事件?
5种
必然事件
不可能事件
随机事件
认识事件
抢答:“从一堆牌中任意抽一张抽到红牌”这一事件是哪些事件?
随机事件
必然事件
不可能事件
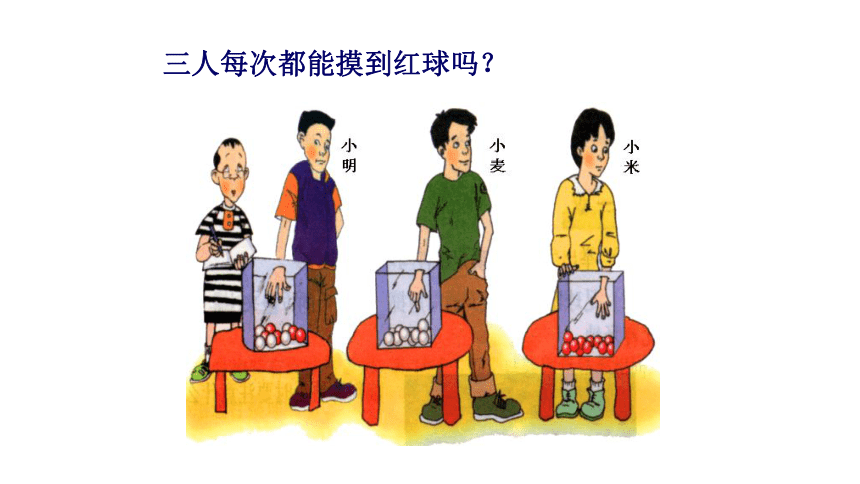
三人每次都能摸到红球吗?
②明天,地球还会转动
③煮熟的鸭子,飞了
④00C以下,这些雪融化
下列现象哪些是必然事件,哪些是不可能事件?
①木柴燃烧,产生热量
打开电视正在播刘翔夺冠的体育片
这两人各买1张彩票,她们中奖了
(5)经过城市中某一有交通信号灯的路口,
遇到红灯;
(4)度量三角形的内角和,结果是360°;
(3)掷一枚骰子,向上的一面是6点;
(2)篮球队员在罚线上投篮一次,未投中;
二、下列事件中,哪些是必然发生的,哪些是不可能
发生的,哪些是随机事件。
(1)通常加热到100℃时,水沸腾;
必然事件
随机事件
随机事件
不可能发生
随机事件
世界是你们的,你说我听
(6)汽车累积行驶1万公里,从未出现故障。
随机事件
(7)抛一枚硬币,正面向上。
随机事件
合作交流:
必然事件
不可能事件
不确定事件
事件
确定事件
必然事件、不可能事件、随机事件各有什么特征?
随机事件
⑴度量三角形内角和,结果是360°.
⑵正常情况下水加热到100°C,就会沸腾.
⑶掷一个正面体的骰子,向上一面点数为6.
⑷经过城市中某一有交通信号灯的路口,遇到红灯.
(5)某射击运动员射击一次,命中靶心.
(不可能事件)
(必然事件)
(随机事件)
(随机事件)
(随机事件)
练一练:
指出下列事件中哪些事件是必然事件,哪些事件是不可以事件,哪些事件是随机事件.
牛刀小试
(6)同一枚骰子连续掷两次,朝上一面出现点数之和为14.
(7)任意四边形的内角和都等于360°.
(8)一辆小汽车从面前经过,它的车牌号码为偶数.
(9)从一副完整扑克牌中任抽一张,它是草花.
(必然事件)
(不可能事件)
(随机事件)
(随机事件)
合作交流:
说说你身边的事件,让同桌判断是哪些事件?
1. 指出下列事件中,哪些是必然事件,哪些是不可能事件,哪些是随机事件?
(1)同旁内角互补,两直线平行。 (2)石河子明天下大雨。 (3)1+1=3。
(4)掷一次骰子,向上一面是6点。 (5)11个人中,至少有两个人出生的月份相同。
(6)中国足球队夺得世界杯冠军。 (7)在装有3个红球的布袋里摸出绿球。
(8)对顶角相等。 (9)太阳从西边下山。 (10)数学测试你得满分。
必然事件是 。不可能事件是: 。随机事件是: 。(写出序号即可)
当堂检测:
中考链接:
1. “a是实数,|a|≥0”这一事件是 ( )
A. 必然事件 B. 不确定事件
C. 不可能事件 D. 随机事件
2. 下列说法中正确的是( )
A.“打开电视,正在播放《新闻联播》”是必然事件;
B.某次抽奖活动中奖的机会为1/100,说明每买100张奖券,一定有一次中奖;
C.数据1,1,2,2,3的众数是3;
D.想了解某市城镇居民人均年收入水平,宜采用抽样调查。
3. 下列事件中,是确定事件的是( )
A.打雷后会下雨 B.明天是睛天
C. 1小时等于60分钟 D.下雨后有彩虹
4.下列事件是必然事件的是( )
A.通常加热到100℃,水沸腾;
B.抛一枚硬币,正面朝上;
C.明天会下雨;
D.经过城市中某一有交通信号灯的路口,恰好遇到红灯。
中考链接:
欣赏
学到了什么:
必然发生的事件
不可能发生的事件
随机事件
事件
确定事件
定义:在一定条件下,有可能发生也有可能不发生称为随机事件
特征:事先不能预料即具有不确定性。
课后作业:
必做题:
1、课本:P131习题25.1 第1题
2、预习课本 P127-128的知识
嘿嘿,这次非让你死不可!
生死签的传说
相传古代有个王国,国王非常阴险而多疑,一位正直的大臣得罪了国王,被判死刑。这个国家世代沿袭着一条奇特的法规:凡是死囚,在临刑前都要抽一次“生死签”(写着“生”和“死”的两张纸条),犯人当众抽签,若抽到“死”签,则立即处死,若抽到“生”签,则当场赦免。
国王一心想处死大臣,与几个心腹密谋,想出一条毒计:暗中让执行官把“生死签”上都写成“死”,两死抽一,必死无疑。
然而在断头台前,聪明的大臣迅速抽出一张签纸塞进嘴里,等到执行官反应过来,签纸早已吞下,大臣故作叹息说:“我听天意,将苦果吞下,只要看剩下的签是什么字就清楚了。”剩下的当然写着“死”字,国王怕犯众怒,只好当众释放了大臣。
国王“机关算尽”,想让大臣死,反而搬起石头砸自己脚,让机智的大臣死里逃生。
嘿嘿,这次非让你死不可!
老臣自有妙计!
思考:
(1)在国王的阴谋中,大臣被处死是什么事件?
(2)在大臣的计策中,大臣被处死是什么事件?
一定条件
必然事件
不可能事件
摸球试验:袋中装有4个黄球,2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出一个球。
(1)这个球是白球还是黄球?
(2)如果两种球都有可能被摸出,那么摸出黄球和摸出白球的可能性一样大吗?
归纳:一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同。
思考:能否通过改变袋子中某种颜色的球的数量,使“摸出黄球”和“摸出白球”的可能性大小相同?
同课章节目录
