人教版数学九年级上册:22.3实际问题与二次函数 课件(共28张PPT)
文档属性
| 名称 | 人教版数学九年级上册:22.3实际问题与二次函数 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 298.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 14:45:44 | ||
图片预览


文档简介
§22.3实际问题与二次函数
——如何巧建平面直角坐标系
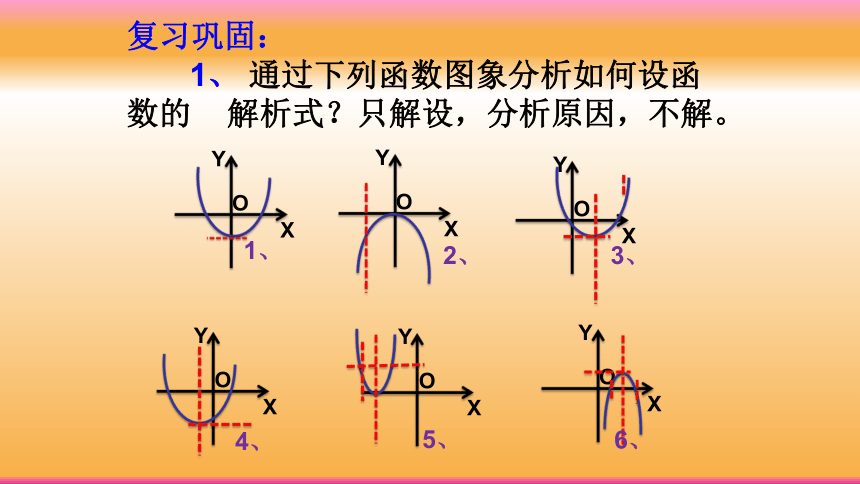
复习巩固:
1、 通过下列函数图象分析如何设函数的 解析式?只解设,分析原因,不解。
O
X
Y
O
X
Y
O
X
Y
O
X
Y
O
X
Y
O
X
Y
1、
2、
3、
4、
5、
6、
2、已知二次函数的图象与X轴
A(-1,0),B(2,0)与
Y轴交于点C(0,2)
(1)求该二次函数的解析式;
(2)写出抛物线的对称轴及顶
点坐标。
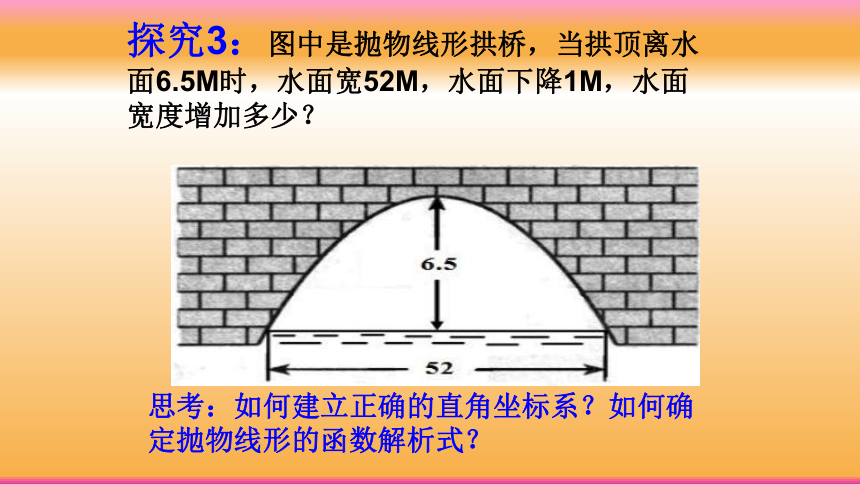
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
思考:如何建立正确的直角坐标系?如何确定抛物线形的函数解析式?
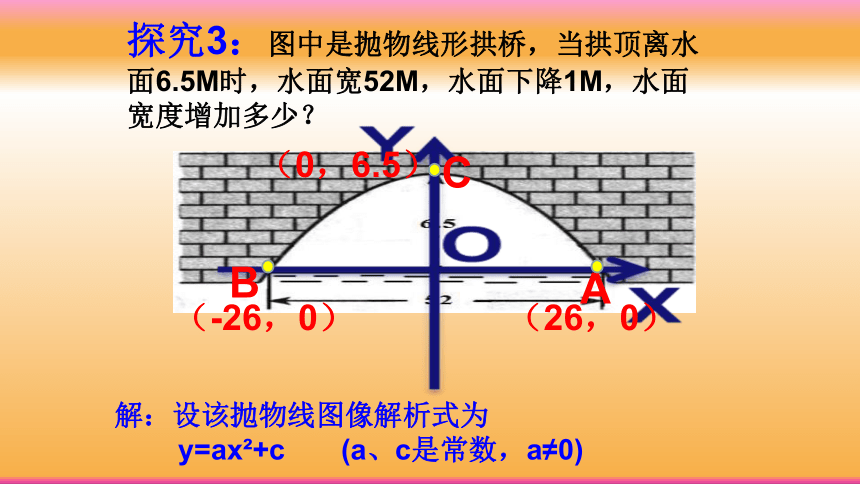
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
C
(26,0)
(0,6.5)
(-26,0)
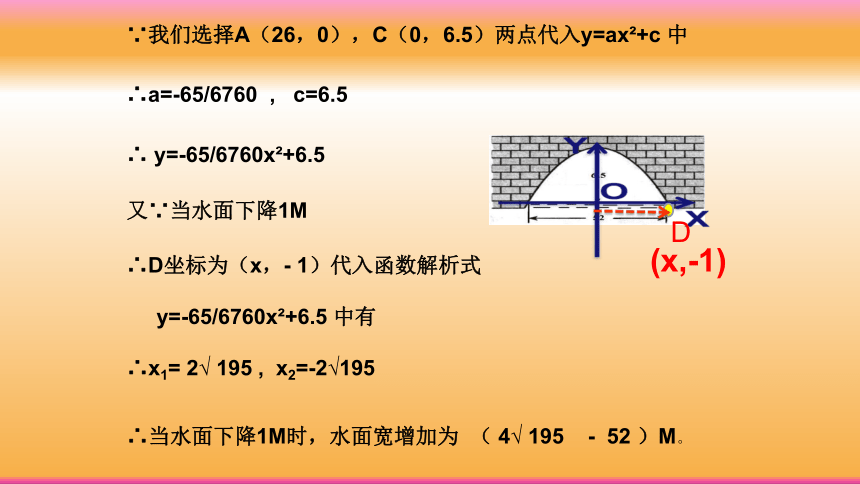
解:设该抛物线图像解析式为
y=ax?+c (a、c是常数,a≠0)
∵我们选择A(26,0),C(0,6.5)两点代入y=ax?+c 中
∴a=-65/6760 , c=6.5
∴ y=-65/6760x?+6.5
又∵当水面下降1M
∴D坐标为(x,- 1)代入函数解析式
y=-65/6760x?+6.5 中有
∴x1= 2√ 195 , x2=-2√195
D
(x,-1)
∴当水面下降1M时,水面宽增加为 ( 4√ 195 - 52 )M。
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
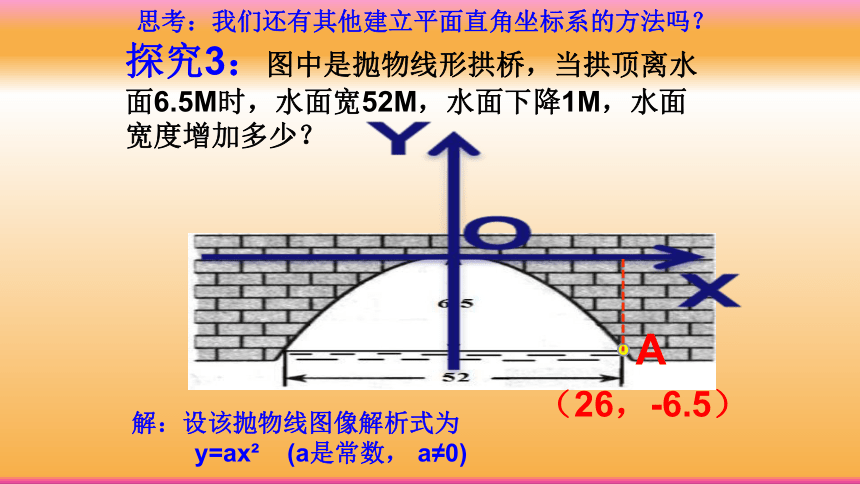
A
(26,-6.5)
解:设该抛物线图像解析式为
y=ax? (a是常数, a≠0)
思考:我们还有其他建立平面直角坐标系的方法吗?
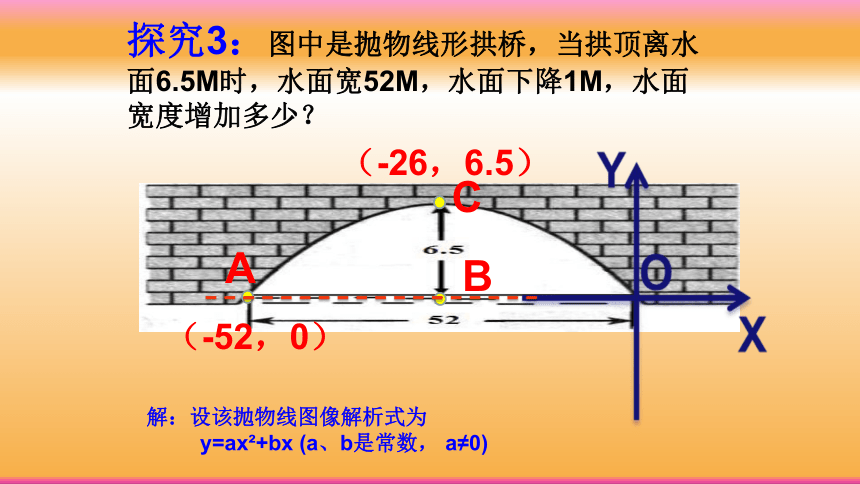
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
(-26,6.5)
(-52,0)
解:设该抛物线图像解析式为
y=ax?+bx (a、b是常数, a≠0)
C
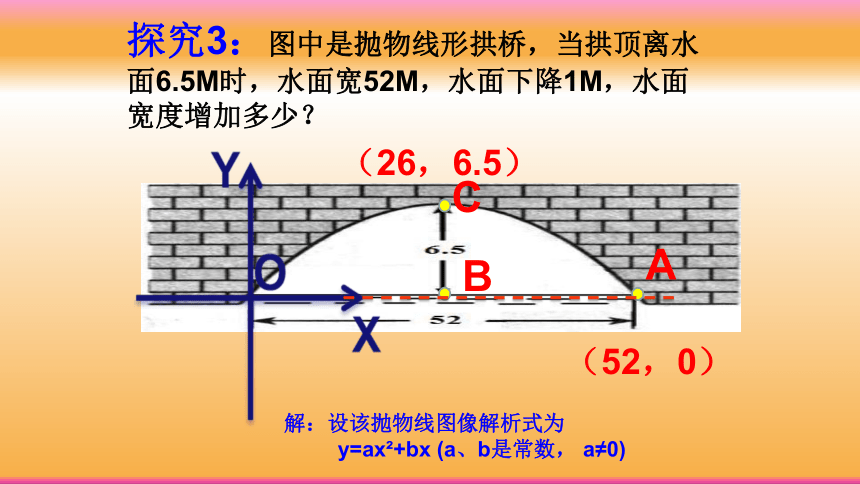
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
(26,6.5)
(52,0)
解:设该抛物线图像解析式为
y=ax?+bx (a、b是常数, a≠0)
C
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
(26,0)
(0,-6.5)
(方法一)
解:设该抛物线图像解析式为
y=a(x+ b/2a)?+(4ac-b2)/4a
(a、b、c是常 数,a≠0)
(方法二)
解:设该抛物线图像解析式为
y=a(x-x1)(x-x2) (a是常
数,a≠0)
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
(-26,0)
(0,-6.5)
(方法一)
解:设该抛物线图像解析式为
y=a(x+ b/2a)?+(4ac-b2)/4a
(a、b、c是常 数,a≠0)
(方法二)
解:设该抛物线图像解析式为
y=a(x-x1)(x-x2) (a是常
数,a≠0)
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
C
(?,0)
(?,6.5)
(?,0)
思考:如果我们解设该抛物线图像解析式为y=ax?+bx+c
(a、b、c是常数,a不等于0),能解吗?为什么?
练 习 (只设函数解析式,分析已知 点坐标,不解函数)
右图是一个工厂的抛物线形水泥建筑大门,大门的地面宽度为4m,两侧距地面3m高处各有一个壁灯,壁灯之间的水平距离为2m ,则工厂门的高为?
4m
3m
2m
练 习 (只设函数解析式,分析已知 点坐标,不解函数)
右图是一个工厂的抛物线形水泥建筑大门,大门的地面宽度为4m,两侧距地面3m高处各有一个壁灯,壁灯之间的水平距离为2m ,则工厂门的高为?
4m
3m
2m
练 习 (只设函数解析式,分析已知 点坐标,不解函数)
右图是一个工厂的抛物线形水泥建筑大门,大门的地面宽度为4m,两侧距地面3m高处各有一个壁灯,壁灯之间的水平距离为2m ,则工厂门的高为?
4m
3m
2m
练 习 (只设函数解析式,分析已知 点坐标,不解函数)
右图是一个工厂的抛物线形水泥建筑大门,大门的地面宽度为4m,两侧距地面3m高处各有一个壁灯,壁灯之间的水平距离为2m ,则工厂门的高为?
4m
3m
2m
练 习 (只设函数解析式,分析已知 点坐标,不解函数)
右图是一个工厂的抛物线形水泥建筑大门,大门的地面宽度为4m,两侧距地面3m高处各有一个壁灯,壁灯之间的水平距离为2m ,则工厂门的高为?
4m
3m
2m
思考:这时能求出吗?
试一试 如图,小明的父亲在相距2M的两棵树间拴了一根绳子,给做了一个简易的秋千。拴绳子的地方距地面高都是2.5M,绳子自然下垂呈抛物线状,身高1M的小明距较近的那棵树0.5M时,头部刚好接触到绳子,则绳子的最低点距地面的距离为?
2M
2.5M
0.5M
1M
试一试 如图,小明的父亲在相距2M的两棵树间拴了一根绳子,给做了一个简易的秋千。拴绳子的地方距地面高都是2.5M,绳子自然下垂呈抛物线状,身高1M的小明距较近的那棵树0.5M时,头部刚好接触到绳子,则绳子的最低点距地面的距离为?
2M
2.5M
0.5M
1M
试一试 如图,小明的父亲在相距2M的两棵树间拴了一根绳子,给做了一个简易的秋千。拴绳子的地方距地面高都是2.5M,绳子自然下垂呈抛物线状,身高1M的小明距较近的那棵树0.5M时,头部刚好接触到绳子,则绳子的最低点距地面的距离为?
2M
2.5M
0.5M
1M
试一试 如图,小明的父亲在相距2M的两棵树间拴了一根绳子,给做了一个简易的秋千。拴绳子的地方距地面高都是2.5M,绳子自然下垂呈抛物线状,身高1M的小明距较近的那棵树0.5M时,头部刚好接触到绳子,则绳子的最低点距地面的距离为?
2M
2.5M
0.5M
1M
试一试 如图,小明的父亲在相距2M的两棵树间拴了一根绳子,给做了一个简易的秋千。拴绳子的地方距地面高都是2.5M,绳子自然下垂呈抛物线状,身高1M的小明距较近的那棵树0.5M时,头部刚好接触到绳子,则绳子的最低点距地面的距离为?
2M
2.5M
0.5M
1M
能力提升:某工厂的大门是一抛物线形水泥建筑物,如图22?10,大门地面宽AB=4米,顶部C离地面的高度为4.4米,现在一辆装满货物的汽车欲通过大门,货物顶部离地面的高度为2.8米,装货宽度为2.4米,请通过计算,判断这辆汽车能否顺利通过大门?
能力提升:某工厂的大门是一抛物线形水泥建筑物,如图22?10,大门地面宽AB=4米,顶部C离地面的高度为4.4米,现在一辆装满货物的汽车欲通过大门,货物顶部离地面的高度为2.8米,装货宽度为2.4米,请通过计算,判断这辆汽车能否顺利通过大门?
能力提升:某工厂的大门是一抛物线形水泥建筑物,如图22?10,大门地面宽AB=4米,顶部C离地面的高度为4.4米,现在一辆装满货物的汽车欲通过大门,货物顶部离地面的高度为2.8米,装货宽度为2.4米,请通过计算,判断这辆汽车能否顺利通过大门?
能力提升:某工厂的大门是一抛物线形水泥建筑物,如图22?10,大门地面宽AB=4米,顶部C离地面的高度为4.4米,现在一辆装满货物的汽车欲通过大门,货物顶部离地面的高度为2.8米,装货宽度为2.4米,请通过计算,判断这辆汽车能否顺利通过大门?
1、分析实际问题,关键是如何巧建立 平面直角坐标系!
2、根据建立的平面直角坐标系,分析函数图像特征,确定已知点的个数,正确列出恰当的函数解析式(关系式);
3、由题中已知找出点的坐标,用“待定系数法”求出未知的系数(参数),确定函数的解析式;
小 结
课后练习
小练习册P27,2
P28,5
大练习册P46,3
P47,4
——如何巧建平面直角坐标系
复习巩固:
1、 通过下列函数图象分析如何设函数的 解析式?只解设,分析原因,不解。
O
X
Y
O
X
Y
O
X
Y
O
X
Y
O
X
Y
O
X
Y
1、
2、
3、
4、
5、
6、
2、已知二次函数的图象与X轴
A(-1,0),B(2,0)与
Y轴交于点C(0,2)
(1)求该二次函数的解析式;
(2)写出抛物线的对称轴及顶
点坐标。
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
思考:如何建立正确的直角坐标系?如何确定抛物线形的函数解析式?
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
C
(26,0)
(0,6.5)
(-26,0)
解:设该抛物线图像解析式为
y=ax?+c (a、c是常数,a≠0)
∵我们选择A(26,0),C(0,6.5)两点代入y=ax?+c 中
∴a=-65/6760 , c=6.5
∴ y=-65/6760x?+6.5
又∵当水面下降1M
∴D坐标为(x,- 1)代入函数解析式
y=-65/6760x?+6.5 中有
∴x1= 2√ 195 , x2=-2√195
D
(x,-1)
∴当水面下降1M时,水面宽增加为 ( 4√ 195 - 52 )M。
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
(26,-6.5)
解:设该抛物线图像解析式为
y=ax? (a是常数, a≠0)
思考:我们还有其他建立平面直角坐标系的方法吗?
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
(-26,6.5)
(-52,0)
解:设该抛物线图像解析式为
y=ax?+bx (a、b是常数, a≠0)
C
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
(26,6.5)
(52,0)
解:设该抛物线图像解析式为
y=ax?+bx (a、b是常数, a≠0)
C
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
(26,0)
(0,-6.5)
(方法一)
解:设该抛物线图像解析式为
y=a(x+ b/2a)?+(4ac-b2)/4a
(a、b、c是常 数,a≠0)
(方法二)
解:设该抛物线图像解析式为
y=a(x-x1)(x-x2) (a是常
数,a≠0)
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
(-26,0)
(0,-6.5)
(方法一)
解:设该抛物线图像解析式为
y=a(x+ b/2a)?+(4ac-b2)/4a
(a、b、c是常 数,a≠0)
(方法二)
解:设该抛物线图像解析式为
y=a(x-x1)(x-x2) (a是常
数,a≠0)
探究3:图中是抛物线形拱桥,当拱顶离水面6.5M时,水面宽52M,水面下降1M,水面宽度增加多少?
A
B
C
(?,0)
(?,6.5)
(?,0)
思考:如果我们解设该抛物线图像解析式为y=ax?+bx+c
(a、b、c是常数,a不等于0),能解吗?为什么?
练 习 (只设函数解析式,分析已知 点坐标,不解函数)
右图是一个工厂的抛物线形水泥建筑大门,大门的地面宽度为4m,两侧距地面3m高处各有一个壁灯,壁灯之间的水平距离为2m ,则工厂门的高为?
4m
3m
2m
练 习 (只设函数解析式,分析已知 点坐标,不解函数)
右图是一个工厂的抛物线形水泥建筑大门,大门的地面宽度为4m,两侧距地面3m高处各有一个壁灯,壁灯之间的水平距离为2m ,则工厂门的高为?
4m
3m
2m
练 习 (只设函数解析式,分析已知 点坐标,不解函数)
右图是一个工厂的抛物线形水泥建筑大门,大门的地面宽度为4m,两侧距地面3m高处各有一个壁灯,壁灯之间的水平距离为2m ,则工厂门的高为?
4m
3m
2m
练 习 (只设函数解析式,分析已知 点坐标,不解函数)
右图是一个工厂的抛物线形水泥建筑大门,大门的地面宽度为4m,两侧距地面3m高处各有一个壁灯,壁灯之间的水平距离为2m ,则工厂门的高为?
4m
3m
2m
练 习 (只设函数解析式,分析已知 点坐标,不解函数)
右图是一个工厂的抛物线形水泥建筑大门,大门的地面宽度为4m,两侧距地面3m高处各有一个壁灯,壁灯之间的水平距离为2m ,则工厂门的高为?
4m
3m
2m
思考:这时能求出吗?
试一试 如图,小明的父亲在相距2M的两棵树间拴了一根绳子,给做了一个简易的秋千。拴绳子的地方距地面高都是2.5M,绳子自然下垂呈抛物线状,身高1M的小明距较近的那棵树0.5M时,头部刚好接触到绳子,则绳子的最低点距地面的距离为?
2M
2.5M
0.5M
1M
试一试 如图,小明的父亲在相距2M的两棵树间拴了一根绳子,给做了一个简易的秋千。拴绳子的地方距地面高都是2.5M,绳子自然下垂呈抛物线状,身高1M的小明距较近的那棵树0.5M时,头部刚好接触到绳子,则绳子的最低点距地面的距离为?
2M
2.5M
0.5M
1M
试一试 如图,小明的父亲在相距2M的两棵树间拴了一根绳子,给做了一个简易的秋千。拴绳子的地方距地面高都是2.5M,绳子自然下垂呈抛物线状,身高1M的小明距较近的那棵树0.5M时,头部刚好接触到绳子,则绳子的最低点距地面的距离为?
2M
2.5M
0.5M
1M
试一试 如图,小明的父亲在相距2M的两棵树间拴了一根绳子,给做了一个简易的秋千。拴绳子的地方距地面高都是2.5M,绳子自然下垂呈抛物线状,身高1M的小明距较近的那棵树0.5M时,头部刚好接触到绳子,则绳子的最低点距地面的距离为?
2M
2.5M
0.5M
1M
试一试 如图,小明的父亲在相距2M的两棵树间拴了一根绳子,给做了一个简易的秋千。拴绳子的地方距地面高都是2.5M,绳子自然下垂呈抛物线状,身高1M的小明距较近的那棵树0.5M时,头部刚好接触到绳子,则绳子的最低点距地面的距离为?
2M
2.5M
0.5M
1M
能力提升:某工厂的大门是一抛物线形水泥建筑物,如图22?10,大门地面宽AB=4米,顶部C离地面的高度为4.4米,现在一辆装满货物的汽车欲通过大门,货物顶部离地面的高度为2.8米,装货宽度为2.4米,请通过计算,判断这辆汽车能否顺利通过大门?
能力提升:某工厂的大门是一抛物线形水泥建筑物,如图22?10,大门地面宽AB=4米,顶部C离地面的高度为4.4米,现在一辆装满货物的汽车欲通过大门,货物顶部离地面的高度为2.8米,装货宽度为2.4米,请通过计算,判断这辆汽车能否顺利通过大门?
能力提升:某工厂的大门是一抛物线形水泥建筑物,如图22?10,大门地面宽AB=4米,顶部C离地面的高度为4.4米,现在一辆装满货物的汽车欲通过大门,货物顶部离地面的高度为2.8米,装货宽度为2.4米,请通过计算,判断这辆汽车能否顺利通过大门?
能力提升:某工厂的大门是一抛物线形水泥建筑物,如图22?10,大门地面宽AB=4米,顶部C离地面的高度为4.4米,现在一辆装满货物的汽车欲通过大门,货物顶部离地面的高度为2.8米,装货宽度为2.4米,请通过计算,判断这辆汽车能否顺利通过大门?
1、分析实际问题,关键是如何巧建立 平面直角坐标系!
2、根据建立的平面直角坐标系,分析函数图像特征,确定已知点的个数,正确列出恰当的函数解析式(关系式);
3、由题中已知找出点的坐标,用“待定系数法”求出未知的系数(参数),确定函数的解析式;
小 结
课后练习
小练习册P27,2
P28,5
大练习册P46,3
P47,4
同课章节目录
