人教版数学九年级上册:22.2二次函数与一元二次方程课件(共19张PPT)
文档属性
| 名称 | 人教版数学九年级上册:22.2二次函数与一元二次方程课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 15:26:16 | ||
图片预览


文档简介
22.2 二次函数与一元二次方程
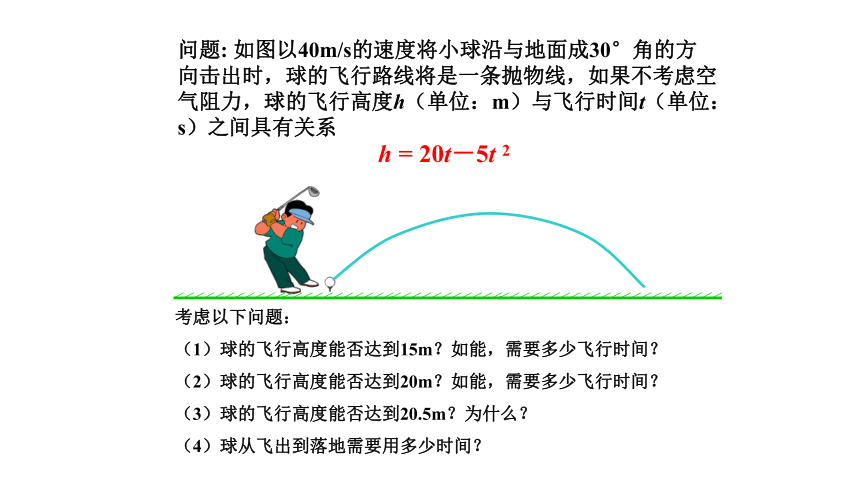
问题: 如图以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系
h = 20t-5t 2
考虑以下问题:
(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?
(2)球的飞行高度能否达到20m?如能,需要多少飞行时间?
(3)球的飞行高度能否达到20.5m?为什么?
(4)球从飞出到落地需要用多少时间?
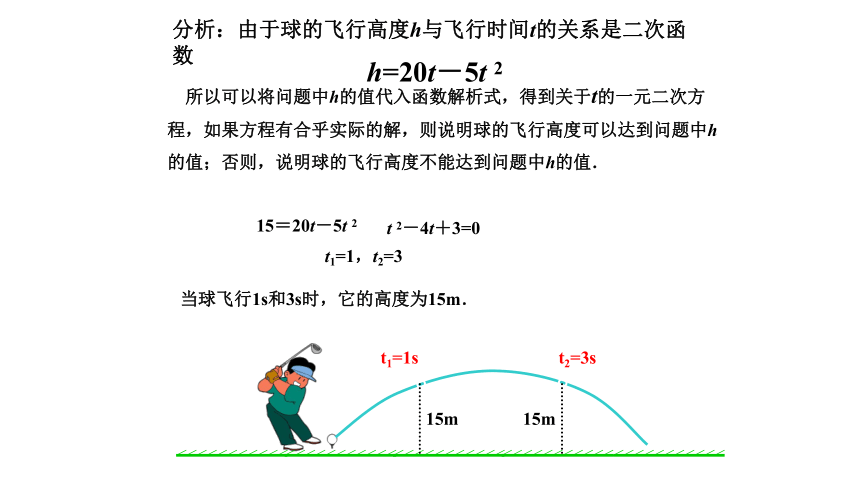
所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方
程,如果方程有合乎实际的解,则说明球的飞行高度可以达到问题中h
的值;否则,说明球的飞行高度不能达到问题中h的值.
解:(1)解方程
15=20t-5t 2
t 2-4t+3=0
t1=1,t2=3
当球飞行1s和3s时,它的高度为15m.
分析:由于球的飞行高度h与飞行时间t的关系是二次函数
h=20t-5t 2
t1=1s
t2=3s
15m
15m
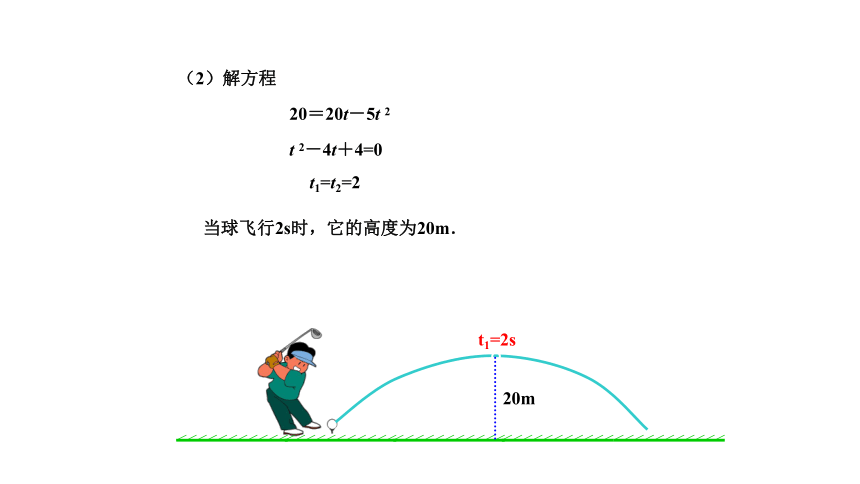
(2)解方程
20=20t-5t 2
t 2-4t+4=0
t1=t2=2
当球飞行2s时,它的高度为20m.
t1=2s
20m
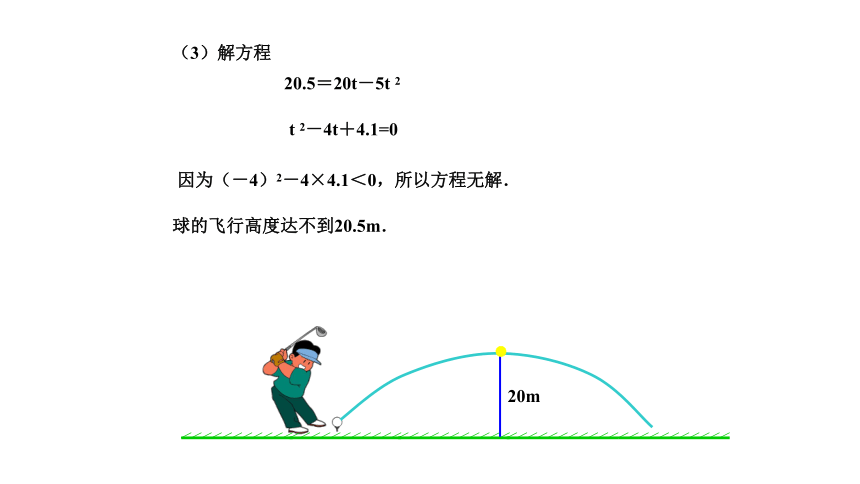
(3)解方程
20.5=20t-5t 2
t 2-4t+4.1=0
因为(-4)2-4×4.1<0,所以方程无解.
球的飞行高度达不到20.5m.
20m
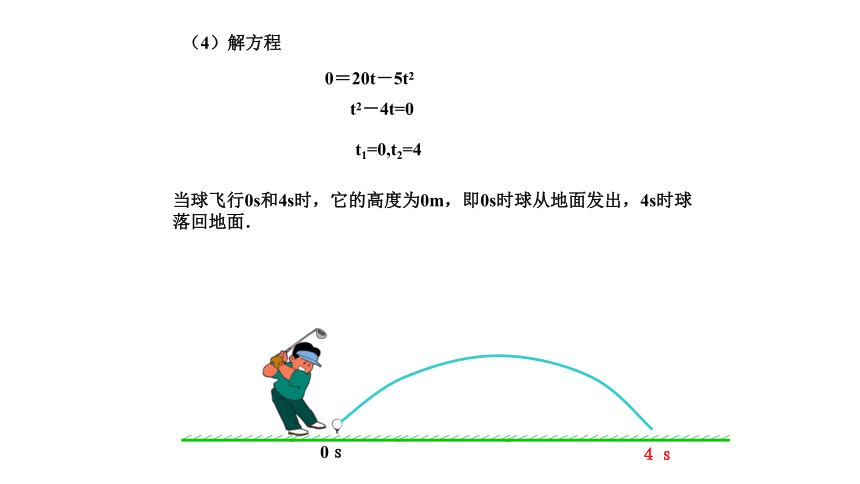
(4)解方程
0=20t-5t2
t2-4t=0
t1=0,t2=4
当球飞行0s和4s时,它的高度为0m,即0s时球从地面发出,4s时球落回地面.
0s
4s
从上面可以看出,二次函数与一元二次方程关系密切.
一般地,我们可以利用二次函数y=ax2+bx+c 深入讨论一元二次方程ax2+bx+c=0
例如,已知二次函数y = -x2+4x的值为3,求自变量x的值,
可以解一元二次方程-x2+4x=3(即x2-4x+3=0).
反过来,解方程x2-4x+3=0 又可
以看作已知二次函数 y = x2-4x+3 的值为0,求自变量x的值.
小组合作,类比探究
问题1:下列二次函数的图象与 x 轴有公共点吗?如果有,公共点的横坐标是多少?
y = x 2 - x + 1
y = x 2 + x - 2
y = x 2 - 6x + 9
y
6
5
4
3
2
1
-1
-2
-3 -2 -1 1 2 3 4 5 6 x
O
小组合作,类比探究
问题2 当 x 取上述公共点的横坐标时,相应的函数值分别是多少?
y = x 2 - x + 1
y = x 2 + x - 2
y = x 2 - 6x + 9
y
6
5
4
3
2
1
-1
-2
-3 -2 -1 1 2 3 4 5 6 x
O
小组合作,类比探究
问题3 由二次函数的图象,你能得出相应的一元二次方程的根吗?二次函数与一元二次方程具有怎样的联系?
x 2 + x - 2 = 0
x 2 - 6x + 9 = 0
x 2 - x + 1 = 0
y = x 2 - x + 1
y = x 2 + x - 2
y = x 2 - 6x + 9
y
6
5
4
3
2
1
-1
-2
-3 -2 -1 1 2 3 4 5 6 x
O
①二次函数 y=x2+x-2 的图象与 x 轴有______个交点,则
一元二次方程 x2+x-1=0 的根的判别式Δ______0.
2
>
②二次函数 y=x2-6x+9 的图像与 x 轴有______个公共点,
则一元二次方程 x2-6x+9=0 的根的判别式Δ______0.
1
=
③二次函数 y=x2-x+1 的图象与 x 轴________公共点,则
一元二次方程 x2-x+1=0 的根的判别式Δ______0.
无
<
归纳:(1)如果抛物线 y=ax2+bx+c 与 x 轴有公共点,公
共点的横坐标是 x0,那么当 x=x0 时,函数的值是____,因此
x=x0 就是方程______________的一个根;反之,一元二次方程
的解就是相应二次函数的图象与x 轴交点的横坐标.
0
ax2+bx+c=0
小组合作,类比探究
归纳(2):
2
两
1
两
0
判别式:b2-4ac
二次函数y=ax2+bx+c与x轴的公共点
一元二次方程ax2+bx+c=0的根
b2-4ac>0
与x轴有____个公共点
有________个不等实数根
b2-4ac=0
与x轴有____个公共点
有________个相等实数根
b2-4ac<0
与x轴有____个公共点
有________个实数根
0
以 a>0 为例列表如下:
b2-4ac的符号
b2-4ac>0
b2-4ac=0
b2-4ac<0
y=ax2+bx+c(a>0)
的图象
关于x的一元二次方程
ax2+bx+c=0的解
归纳(3):
【例 1】 已知二次函数 y=mx2-6x+1(m 是常数)的图象与
x 轴只有一个公共点,求 m 的值.
解:∵二次函数 y=mx2-6x+1的图象与 x 轴只有一
个公共点,
∴二次方程 mx2-6x+1=0 有两个相等的实数根.
∴(-6)2-4m=0且 ,解得 m=9.
故 m 的值为9.
变式:把题中“二次”两字去掉,即题目是:
已知函数 y=mx2-6x+1(m 是常数)的图象与x 轴只有一个公共点,求 m 的值.
【例 2】已知抛物线y=2(k+1)x2+4kx+2k-3.
(1)当k为何值时,抛物线与x轴有两个公共点?
(2)当k为何值时,抛物线与x轴只有一个公共点?
(3)当k为何值时,抛物线与x轴没有公共点?
【例 3】已知抛物线y=x2+mx+m-2.
求证:无论m取何值,抛物线总与x轴有两个交点.
【跟踪训练】
C
1.函数 y=x2-2x-1 的图象与 x 轴的交点个数有(
)
A.0 个
B.1 个
C.2 个
D.3 个
2.若抛物线 y=(a-1)x2+2x+1 与 x 轴只有一个公共点,
则a的值为________.
2
3.若关于x的一元二次方程 x2-2x+m=0 有两个相等的实数根,则m= ,此时抛物线y=x2-2x+m与 x 轴有 个公共点.
4.已知抛物线y=x2-8x+c的顶点在x 轴上,则c= .
5.一元二次方程 3x2+x-10=0 的两个根是x1=-2,x2= ,那么二次函数y= 3x2+x-10的图象与x 轴的交点坐标是 .
6.抛物线y= x2-3x-4与y 轴交于点 ,与x 轴交于点 .
1
1
16
(-2,0)、(5/3,0)
(-1,0)、(4,0)
(0,-4)
今天我的收获……
一般地,从二次函数 y = ax 2 + bx + c 的图象可知:
(1)如果抛物线 y = ax 2 + bx + c 与 x 轴有公共点,
公共点的横坐标是 x0,那么当 x = x0 时,函数值是 0,
因此 x = x0 是方程 ax 2 + bx + c = 0 的一个根.反之,一元二次方程的解就是二次函数的图象与x 轴交点的横坐标。
(2)二次函数 y = ax 2 + bx + c 的图象与 x 轴的位置
关系有三种:没有公共点,有一个公共点,有两个公共
点. 这对应着一元二次方程 ax 2 + bx + c = 0 的根的三种
情况:没有实数根,有两个相等的实数根,有两个不等
的实数根.
问题: 如图以40m/s的速度将小球沿与地面成30°角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有关系
h = 20t-5t 2
考虑以下问题:
(1)球的飞行高度能否达到15m?如能,需要多少飞行时间?
(2)球的飞行高度能否达到20m?如能,需要多少飞行时间?
(3)球的飞行高度能否达到20.5m?为什么?
(4)球从飞出到落地需要用多少时间?
所以可以将问题中h的值代入函数解析式,得到关于t的一元二次方
程,如果方程有合乎实际的解,则说明球的飞行高度可以达到问题中h
的值;否则,说明球的飞行高度不能达到问题中h的值.
解:(1)解方程
15=20t-5t 2
t 2-4t+3=0
t1=1,t2=3
当球飞行1s和3s时,它的高度为15m.
分析:由于球的飞行高度h与飞行时间t的关系是二次函数
h=20t-5t 2
t1=1s
t2=3s
15m
15m
(2)解方程
20=20t-5t 2
t 2-4t+4=0
t1=t2=2
当球飞行2s时,它的高度为20m.
t1=2s
20m
(3)解方程
20.5=20t-5t 2
t 2-4t+4.1=0
因为(-4)2-4×4.1<0,所以方程无解.
球的飞行高度达不到20.5m.
20m
(4)解方程
0=20t-5t2
t2-4t=0
t1=0,t2=4
当球飞行0s和4s时,它的高度为0m,即0s时球从地面发出,4s时球落回地面.
0s
4s
从上面可以看出,二次函数与一元二次方程关系密切.
一般地,我们可以利用二次函数y=ax2+bx+c 深入讨论一元二次方程ax2+bx+c=0
例如,已知二次函数y = -x2+4x的值为3,求自变量x的值,
可以解一元二次方程-x2+4x=3(即x2-4x+3=0).
反过来,解方程x2-4x+3=0 又可
以看作已知二次函数 y = x2-4x+3 的值为0,求自变量x的值.
小组合作,类比探究
问题1:下列二次函数的图象与 x 轴有公共点吗?如果有,公共点的横坐标是多少?
y = x 2 - x + 1
y = x 2 + x - 2
y = x 2 - 6x + 9
y
6
5
4
3
2
1
-1
-2
-3 -2 -1 1 2 3 4 5 6 x
O
小组合作,类比探究
问题2 当 x 取上述公共点的横坐标时,相应的函数值分别是多少?
y = x 2 - x + 1
y = x 2 + x - 2
y = x 2 - 6x + 9
y
6
5
4
3
2
1
-1
-2
-3 -2 -1 1 2 3 4 5 6 x
O
小组合作,类比探究
问题3 由二次函数的图象,你能得出相应的一元二次方程的根吗?二次函数与一元二次方程具有怎样的联系?
x 2 + x - 2 = 0
x 2 - 6x + 9 = 0
x 2 - x + 1 = 0
y = x 2 - x + 1
y = x 2 + x - 2
y = x 2 - 6x + 9
y
6
5
4
3
2
1
-1
-2
-3 -2 -1 1 2 3 4 5 6 x
O
①二次函数 y=x2+x-2 的图象与 x 轴有______个交点,则
一元二次方程 x2+x-1=0 的根的判别式Δ______0.
2
>
②二次函数 y=x2-6x+9 的图像与 x 轴有______个公共点,
则一元二次方程 x2-6x+9=0 的根的判别式Δ______0.
1
=
③二次函数 y=x2-x+1 的图象与 x 轴________公共点,则
一元二次方程 x2-x+1=0 的根的判别式Δ______0.
无
<
归纳:(1)如果抛物线 y=ax2+bx+c 与 x 轴有公共点,公
共点的横坐标是 x0,那么当 x=x0 时,函数的值是____,因此
x=x0 就是方程______________的一个根;反之,一元二次方程
的解就是相应二次函数的图象与x 轴交点的横坐标.
0
ax2+bx+c=0
小组合作,类比探究
归纳(2):
2
两
1
两
0
判别式:b2-4ac
二次函数y=ax2+bx+c与x轴的公共点
一元二次方程ax2+bx+c=0的根
b2-4ac>0
与x轴有____个公共点
有________个不等实数根
b2-4ac=0
与x轴有____个公共点
有________个相等实数根
b2-4ac<0
与x轴有____个公共点
有________个实数根
0
以 a>0 为例列表如下:
b2-4ac的符号
b2-4ac>0
b2-4ac=0
b2-4ac<0
y=ax2+bx+c(a>0)
的图象
关于x的一元二次方程
ax2+bx+c=0的解
归纳(3):
【例 1】 已知二次函数 y=mx2-6x+1(m 是常数)的图象与
x 轴只有一个公共点,求 m 的值.
解:∵二次函数 y=mx2-6x+1的图象与 x 轴只有一
个公共点,
∴二次方程 mx2-6x+1=0 有两个相等的实数根.
∴(-6)2-4m=0且 ,解得 m=9.
故 m 的值为9.
变式:把题中“二次”两字去掉,即题目是:
已知函数 y=mx2-6x+1(m 是常数)的图象与x 轴只有一个公共点,求 m 的值.
【例 2】已知抛物线y=2(k+1)x2+4kx+2k-3.
(1)当k为何值时,抛物线与x轴有两个公共点?
(2)当k为何值时,抛物线与x轴只有一个公共点?
(3)当k为何值时,抛物线与x轴没有公共点?
【例 3】已知抛物线y=x2+mx+m-2.
求证:无论m取何值,抛物线总与x轴有两个交点.
【跟踪训练】
C
1.函数 y=x2-2x-1 的图象与 x 轴的交点个数有(
)
A.0 个
B.1 个
C.2 个
D.3 个
2.若抛物线 y=(a-1)x2+2x+1 与 x 轴只有一个公共点,
则a的值为________.
2
3.若关于x的一元二次方程 x2-2x+m=0 有两个相等的实数根,则m= ,此时抛物线y=x2-2x+m与 x 轴有 个公共点.
4.已知抛物线y=x2-8x+c的顶点在x 轴上,则c= .
5.一元二次方程 3x2+x-10=0 的两个根是x1=-2,x2= ,那么二次函数y= 3x2+x-10的图象与x 轴的交点坐标是 .
6.抛物线y= x2-3x-4与y 轴交于点 ,与x 轴交于点 .
1
1
16
(-2,0)、(5/3,0)
(-1,0)、(4,0)
(0,-4)
今天我的收获……
一般地,从二次函数 y = ax 2 + bx + c 的图象可知:
(1)如果抛物线 y = ax 2 + bx + c 与 x 轴有公共点,
公共点的横坐标是 x0,那么当 x = x0 时,函数值是 0,
因此 x = x0 是方程 ax 2 + bx + c = 0 的一个根.反之,一元二次方程的解就是二次函数的图象与x 轴交点的横坐标。
(2)二次函数 y = ax 2 + bx + c 的图象与 x 轴的位置
关系有三种:没有公共点,有一个公共点,有两个公共
点. 这对应着一元二次方程 ax 2 + bx + c = 0 的根的三种
情况:没有实数根,有两个相等的实数根,有两个不等
的实数根.
同课章节目录
