人教版数学九年级上册:23.2.1中心对称课件(共36张PPT)
文档属性
| 名称 | 人教版数学九年级上册:23.2.1中心对称课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 00:00:00 | ||
图片预览



文档简介
23.2 中心对称
观察下面的图形,你有什么发现?
观察下面的几个图形你有什么发现?
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
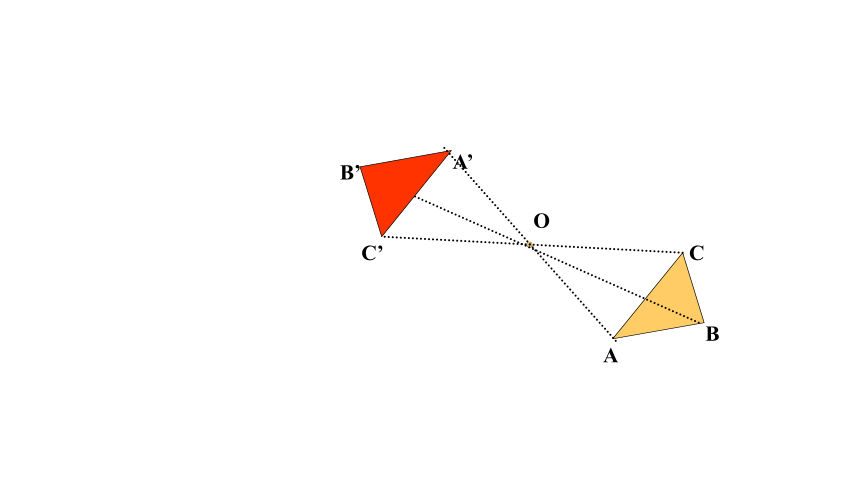
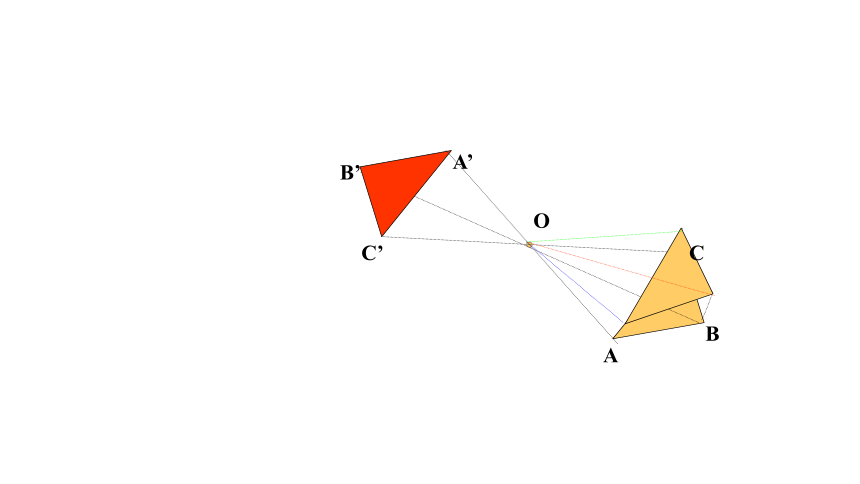
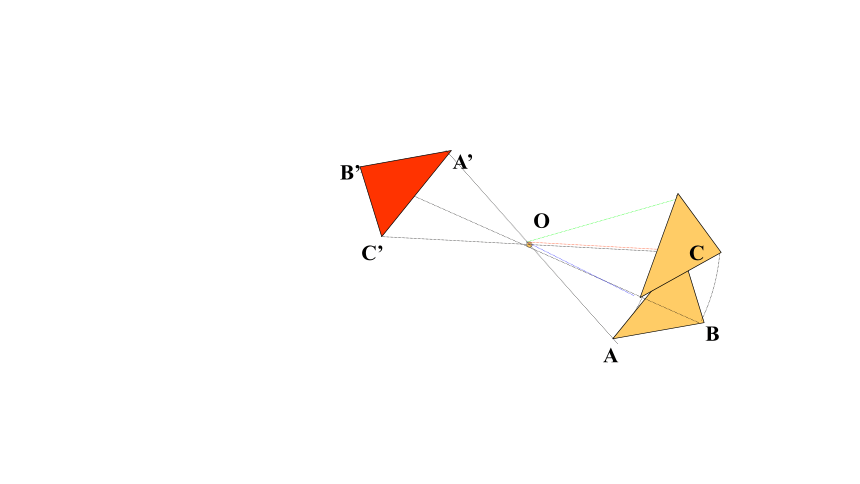
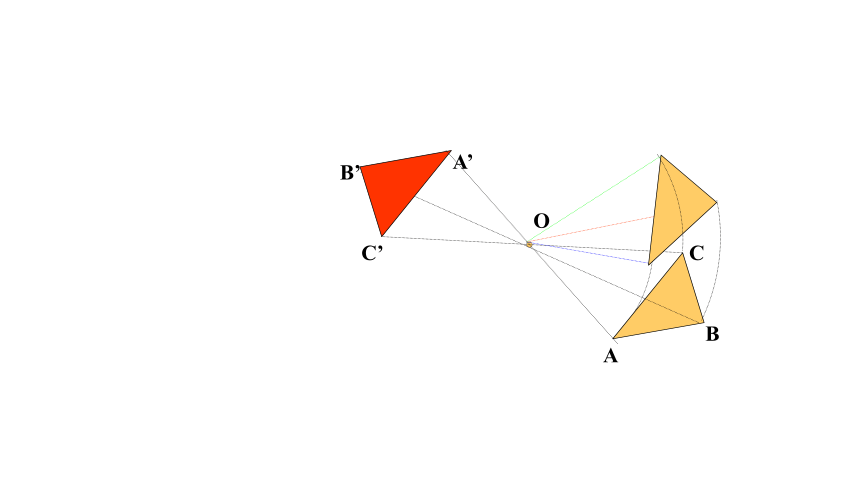
(1)把其中一个图案绕点O旋转180°,你有什么发现?
观 察
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现?
O
C
B
(2)
重合
重合
概念
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称,也称这两个图形成中心对称
A
B
C
A’
C’
B’
O
这个点叫作对称中心
2个图形中的对应点叫做对称点
下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?
探索:
A’
B’
C’
A
B
C
O
(1)OA=OA′、OB=OB′、 OC=OC′
(2)△ABC≌△A′B′C′
归纳:
(1)在成中心对称的两个图形中,连接对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
(2)关于中心对称的两个图形是全等形。
(2)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分.
(1)关于中心对称的两个图形是全等形;
归纳性质
A
A′
B′
B
O
2、线段的中心对称线段的作法
A
O
A′
1、点的中心对称点的作法
灵活运用,体会内涵
以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
点A′即为所求的点
例1 (2)如图23.2-5,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.
解:
A′
C′
B′
△A′B′C′即为所求的三角形。
3.已知四边形ABCD和点O,画四边形A’B’C’D’,使它
与已知四边形关于点O对称。
.
.
画法:1. 连结AO并延长到A’,使OA’=OA,得到点A的对称点A’.
2. 同样画B、C、D的对称点B’、C’、D’.
3. 顺次连结A’、B’、C’、D’各点.
四边形A’B’C’D’就是所求的四边形.
A ’
B’
D’
C’
.
D
C
B
A
o
A
B
C
D
O
∴四边形A`B`C`D是
所求的四边形。
A`
.
D`
.
C`
.
B`
.
若点O是BC的中点呢?
A
B
C
D
∴四边形A`B`C`D`就是
所求的四边形。
A`
D`
.
C`
.
B`
.
若点O与点A重合呢?
如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
A
B
C
A’
B’
C’
应用
解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)
A
B
C
A’
B’
C’
O
O
解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。
A
B
C
A’
B’
C’
轴对称 与中心对称定义、性质对比图:
轴对称
中心对称
定
义
1
2
3
有一条对称轴—直线
图形沿轴对折,(翻转达180度。)
翻转后与另一个图形重合。
有一个对称中心—点。
图形绕中心旋转180度。
旋转后与另一个图形重合。
性
质
1
2
两个图形是全等形。
对称轴是对称点连线的垂直平分线。
两个图形是全等形。
对称点连线都过对称中心,
且被对称中心平分。
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
A
B
C
C
1
A
1
B
1
O
想一想
教学反思
本节课你有哪些收获与疑问?
作业布置:
课堂作业:
P68 习题23.2 1、7
课后作业:
基础训练相应内容
观察下面的图形,你有什么发现?
观察下面的几个图形你有什么发现?
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
A
B
C
A’
C’
B’
O
(1)把其中一个图案绕点O旋转180°,你有什么发现?
观 察
(2)线段AC,BD相交于点O,OA=OC,OB=OD.把 △OCD绕点O旋转180°,你有什么发现?
O
C
B
(2)
重合
重合
概念
把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称,也称这两个图形成中心对称
A
B
C
A’
C’
B’
O
这个点叫作对称中心
2个图形中的对应点叫做对称点
下图中△A′B′C′与△ABC关于点O是成中心对称的,你能从图中找到哪些等量关系?
探索:
A’
B’
C’
A
B
C
O
(1)OA=OA′、OB=OB′、 OC=OC′
(2)△ABC≌△A′B′C′
归纳:
(1)在成中心对称的两个图形中,连接对称点的线段都经过对称中心,并且被对称中心平分.
反过来,如果两个图形的对应点连成的线段都经过某一点,并且都被该点平分,那么这两个图形一定关于这一点成中心对称.
(2)关于中心对称的两个图形是全等形。
(2)关于中心对称的两个图形,对称点所连线段都经过对称中心,而且被对称中心平分.
(1)关于中心对称的两个图形是全等形;
归纳性质
A
A′
B′
B
O
2、线段的中心对称线段的作法
A
O
A′
1、点的中心对称点的作法
灵活运用,体会内涵
以点O为对称中心,作出点A的对称点A′;
以点O为对称中心,作出线段AB的对称线段点A′B′
点A′即为所求的点
例1 (2)如图23.2-5,选择点O为对称中心,画出与
△ABC关于点O对称的△A′B′C′.
解:
A′
C′
B′
△A′B′C′即为所求的三角形。
3.已知四边形ABCD和点O,画四边形A’B’C’D’,使它
与已知四边形关于点O对称。
.
.
画法:1. 连结AO并延长到A’,使OA’=OA,得到点A的对称点A’.
2. 同样画B、C、D的对称点B’、C’、D’.
3. 顺次连结A’、B’、C’、D’各点.
四边形A’B’C’D’就是所求的四边形.
A ’
B’
D’
C’
.
D
C
B
A
o
A
B
C
D
O
∴四边形A`B`C`D是
所求的四边形。
A`
.
D`
.
C`
.
B`
.
若点O是BC的中点呢?
A
B
C
D
∴四边形A`B`C`D`就是
所求的四边形。
A`
D`
.
C`
.
B`
.
若点O与点A重合呢?
如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O。
A
B
C
A’
B’
C’
应用
解法一:根据观察,B、B’应是对应点,连结BB’,用刻度尺找出BB’的中点O,则点O即为所求(如图)
A
B
C
A’
B’
C’
O
O
解法二:根据观察,B、B’及C、C’应是两组对应点,连结BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)。
A
B
C
A’
B’
C’
轴对称 与中心对称定义、性质对比图:
轴对称
中心对称
定
义
1
2
3
有一条对称轴—直线
图形沿轴对折,(翻转达180度。)
翻转后与另一个图形重合。
有一个对称中心—点。
图形绕中心旋转180度。
旋转后与另一个图形重合。
性
质
1
2
两个图形是全等形。
对称轴是对称点连线的垂直平分线。
两个图形是全等形。
对称点连线都过对称中心,
且被对称中心平分。
轴 对 称
中心对称
1
有一条对称轴
——
直线
有一个对称中心
——
点
2
图形沿轴对折(翻转
180°
)
图形绕中心旋转
180°
3
翻转后和另一个图形重合
旋转后和另一个图形重合
A
B
C
C
1
A
1
B
1
O
想一想
教学反思
本节课你有哪些收获与疑问?
作业布置:
课堂作业:
P68 习题23.2 1、7
课后作业:
基础训练相应内容
同课章节目录
