人教版数学九年级上册:24.1.1圆课件(共27张PPT)
文档属性
| 名称 | 人教版数学九年级上册:24.1.1圆课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 17:59:38 | ||
图片预览








文档简介
24.1.1 圆
人教版九年级
圆是一种和谐、美丽的图形,无论从哪个角度看,它都具有同一形状。
古希腊的数学家毕达哥拉斯认为:“一切立体图形中最美的是球,一切平面图形中最美的是圆”。
学习目标
1.了解圆的两种定义,以及识别圆的相关概
念。
2.掌握四点共圆的证明方法。
3.利用圆的概念解决简单问题,形成几何直观,增强应用意识。
学习重点
经历形成圆的概念的过程,理解圆及其有关概念。
说一说
你能举例说明生活中哪些物体是圆形的吗?
我知道!!
美妙的圆
圆是生活中常见的图形,许多物体都给我们以圆的形象
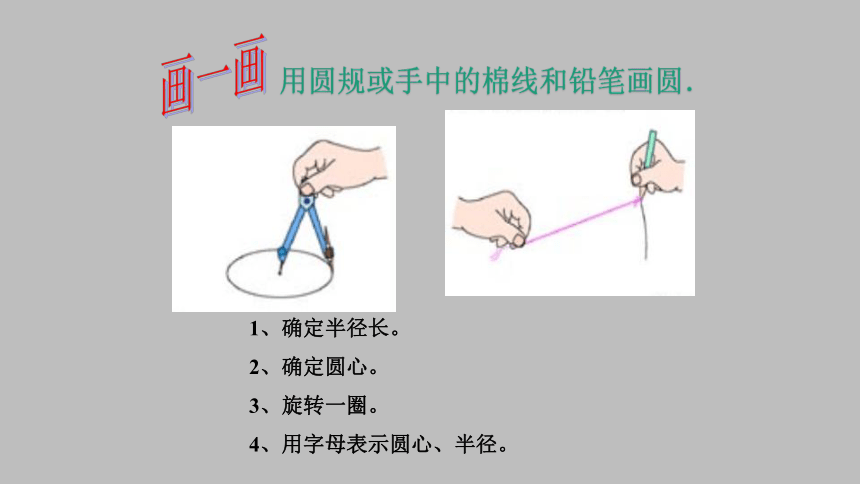
用圆规或手中的棉线和铅笔画圆.
画一画
1、确定半径长。
2、确定圆心。
3、旋转一圈。
4、用字母表示圆心、半径。
在一个平面内,线段OP绕它固定的一个端点O旋转一周,另一个端点P所形成的图形叫做-------圆
观察以上两种画圆的过程,你能由此说出圆的形成过程吗
一、圆的定义
※固定的端点O 叫做圆心
※线段OP 叫做半径
※以点O为圆心的圆,
记作“⊙O”,读作“圆O”.
O
A
r
圆上任意一点到圆心的距离相等吗?反过来,平面内到点O的距离等于线段OA的长的点都在圆上吗?
量一量
(2) 到定点的距离都等于定长的点都在同一个圆上.
(1)圆上各点到圆心O(定点)的距离都等于 半径r(定长)
圆(集合定义):圆心为O、半径为r的圆可以看成是到定点O的距离等于定长r 的点的集合.
圆,一中同长也
----墨子
圆的两种定义
旋转定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
集合定义:到定点O的距离等于定长r 的点集合,可以看成是圆心为O、半径为r的圆
同心圆
等圆
确定一个圆的要素
圆心与半径
圆心相同,半径不同
半径相同,圆心不同
看一看
想一想
如何确定一个唯一的圆?
同步练习
1、填空:
(1)根据圆的定义,“圆”指的是“ ”,而不是“圆面”。
(2)圆心和半径是确定一个圆的两个必需条件,圆心决定圆的 ,半径决定圆的 ,二者缺一不可。
圆周
位置
大小
圆形车轮为什么平稳?
经过圆心的弦(如图中的AB)叫做直径.
·
C
O
A
连接圆上任意两点的线段(如图AC)叫做弦,
二、与圆有关的概念
弦
B
注意:
凡直径都是弦,是圆中最长的弦,但弦不一定是直径.
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 ,读作“圆弧AB”或“弧AB”.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
O
A
B
弧
⌒
AB
·
B
O
A
·
C
O
A
B
劣弧与优弧
小于半圆的弧(如图中的 )叫做劣弧;
⌒
AC
大于半圆的弧(用三个字母表示,
如图中的 )叫做优弧.
ABC
⌒
弧有三类,分别是优弧、劣弧、半圆。
由弧及其所对的弦组成的图形叫弓形图。
提醒:知道弧的两个起点,不能判断它是优弧还是劣弧,需分情况讨论。
等圆
能够重合的两个圆是等圆。
容易看出:半径相等的两个圆是等圆;
反过来,同圆或等圆的半径相等。
·
B
O1
A
等弧
在同圆或等圆中,能够互相重合的弧叫做等弧。
·
D
O2
F
E
C
思考:长度相等的弧是等弧吗?
同心圆:圆心相同而半径不等的两个圆或多个圆。
同心圆
想一想
判断下列说法的正误:
(1)弦是直径;( )
(2)半圆是弧; ( )
(3)过圆心的线段是直径; ( )
(7)圆心相同,半径相等的两个圆是同心圆;( )
(8)半径相等的两个圆是等圆.( )
(4)过圆心的直线是直径;( )
(5)半圆是最长的弧;( )
(6)直径是最长的弦;( )
活动三 巩固练习
●
O
B
C
A
1.如图,弦有:______________
⌒
AB
⌒
BC
2 .劣弧有:
优弧有:
⌒
ACB
⌒
BAC
你知道优弧与劣弧的区别么?
AB BC AC
⌒
ABC
⌒
ACB
⌒
BCA
它们一样么?
思考题
已知:矩形ABCD的对角线AC、BD相交于O。
求证:A、B、C、D在以O为圆心的同一圆上。
A
B
C
D
O
证明:∵四边形ABCD是矩形
∴AO=OC;OB=OD;
又∵AC=BD
∴OA=OB=OC=OD
∴A、B、C、D在以O为圆心以OA为半径的圆上。
例:如图,若AD,BE都是△ABC的高。讨论A、B、D、E四点在同一个圆上吗?
A
A
A
B
C
D
E
O
议一议
请同学们谈谈你的收获和困惑-------
作业:1、课本P81第2题、第3题
2、《能力培养与测试》66页---67页
结束寄语
生活是美的,数学也是美的,
我们要用发现美的眼光看待生活,
更要用发现美的眼光对待数学。
人教版九年级
圆是一种和谐、美丽的图形,无论从哪个角度看,它都具有同一形状。
古希腊的数学家毕达哥拉斯认为:“一切立体图形中最美的是球,一切平面图形中最美的是圆”。
学习目标
1.了解圆的两种定义,以及识别圆的相关概
念。
2.掌握四点共圆的证明方法。
3.利用圆的概念解决简单问题,形成几何直观,增强应用意识。
学习重点
经历形成圆的概念的过程,理解圆及其有关概念。
说一说
你能举例说明生活中哪些物体是圆形的吗?
我知道!!
美妙的圆
圆是生活中常见的图形,许多物体都给我们以圆的形象
用圆规或手中的棉线和铅笔画圆.
画一画
1、确定半径长。
2、确定圆心。
3、旋转一圈。
4、用字母表示圆心、半径。
在一个平面内,线段OP绕它固定的一个端点O旋转一周,另一个端点P所形成的图形叫做-------圆
观察以上两种画圆的过程,你能由此说出圆的形成过程吗
一、圆的定义
※固定的端点O 叫做圆心
※线段OP 叫做半径
※以点O为圆心的圆,
记作“⊙O”,读作“圆O”.
O
A
r
圆上任意一点到圆心的距离相等吗?反过来,平面内到点O的距离等于线段OA的长的点都在圆上吗?
量一量
(2) 到定点的距离都等于定长的点都在同一个圆上.
(1)圆上各点到圆心O(定点)的距离都等于 半径r(定长)
圆(集合定义):圆心为O、半径为r的圆可以看成是到定点O的距离等于定长r 的点的集合.
圆,一中同长也
----墨子
圆的两种定义
旋转定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫做圆.
集合定义:到定点O的距离等于定长r 的点集合,可以看成是圆心为O、半径为r的圆
同心圆
等圆
确定一个圆的要素
圆心与半径
圆心相同,半径不同
半径相同,圆心不同
看一看
想一想
如何确定一个唯一的圆?
同步练习
1、填空:
(1)根据圆的定义,“圆”指的是“ ”,而不是“圆面”。
(2)圆心和半径是确定一个圆的两个必需条件,圆心决定圆的 ,半径决定圆的 ,二者缺一不可。
圆周
位置
大小
圆形车轮为什么平稳?
经过圆心的弦(如图中的AB)叫做直径.
·
C
O
A
连接圆上任意两点的线段(如图AC)叫做弦,
二、与圆有关的概念
弦
B
注意:
凡直径都是弦,是圆中最长的弦,但弦不一定是直径.
圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 ,读作“圆弧AB”或“弧AB”.
圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
O
A
B
弧
⌒
AB
·
B
O
A
·
C
O
A
B
劣弧与优弧
小于半圆的弧(如图中的 )叫做劣弧;
⌒
AC
大于半圆的弧(用三个字母表示,
如图中的 )叫做优弧.
ABC
⌒
弧有三类,分别是优弧、劣弧、半圆。
由弧及其所对的弦组成的图形叫弓形图。
提醒:知道弧的两个起点,不能判断它是优弧还是劣弧,需分情况讨论。
等圆
能够重合的两个圆是等圆。
容易看出:半径相等的两个圆是等圆;
反过来,同圆或等圆的半径相等。
·
B
O1
A
等弧
在同圆或等圆中,能够互相重合的弧叫做等弧。
·
D
O2
F
E
C
思考:长度相等的弧是等弧吗?
同心圆:圆心相同而半径不等的两个圆或多个圆。
同心圆
想一想
判断下列说法的正误:
(1)弦是直径;( )
(2)半圆是弧; ( )
(3)过圆心的线段是直径; ( )
(7)圆心相同,半径相等的两个圆是同心圆;( )
(8)半径相等的两个圆是等圆.( )
(4)过圆心的直线是直径;( )
(5)半圆是最长的弧;( )
(6)直径是最长的弦;( )
活动三 巩固练习
●
O
B
C
A
1.如图,弦有:______________
⌒
AB
⌒
BC
2 .劣弧有:
优弧有:
⌒
ACB
⌒
BAC
你知道优弧与劣弧的区别么?
AB BC AC
⌒
ABC
⌒
ACB
⌒
BCA
它们一样么?
思考题
已知:矩形ABCD的对角线AC、BD相交于O。
求证:A、B、C、D在以O为圆心的同一圆上。
A
B
C
D
O
证明:∵四边形ABCD是矩形
∴AO=OC;OB=OD;
又∵AC=BD
∴OA=OB=OC=OD
∴A、B、C、D在以O为圆心以OA为半径的圆上。
例:如图,若AD,BE都是△ABC的高。讨论A、B、D、E四点在同一个圆上吗?
A
A
A
B
C
D
E
O
议一议
请同学们谈谈你的收获和困惑-------
作业:1、课本P81第2题、第3题
2、《能力培养与测试》66页---67页
结束寄语
生活是美的,数学也是美的,
我们要用发现美的眼光看待生活,
更要用发现美的眼光对待数学。
同课章节目录
