人教版数学九年级上册:24.1.3弦、弧、圆心角课件(共21张PPT)
文档属性
| 名称 | 人教版数学九年级上册:24.1.3弦、弧、圆心角课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 357.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 00:00:00 | ||
图片预览





文档简介
弧、弦、圆心角
(1)圆是轴对称图形,其对称轴是任意一条过圆心的直线。
(2)垂直于弦的直径平分弦,并且平分弦所对的弧。
(3)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
以旧引新
活动1
现象一:一块圆形的蛋糕,糕点师只要过圆心点在互相垂直的两个方向上切两刀,不管糕点师站在哪里,分成的四块一定是均等的。 这个现象跟圆的哪个性质有关?
探究一:圆的中心对称性
想一想:这些现象说明了什么?
说明对折后能够完全重合,只要是过圆心的直线,分成的两部分均对称,说明圆是轴对称图形,对称轴是过圆心的任一条直线。
以旧引新
活动1
现象二:机械式闹钟上钟时,每次只要转动发条上的钟钮 180°时,看上去跟没转动以前是一个样的。这个现象跟圆的哪个性质有关?
探究一:圆的中心对称性
想一想:这些现象说明了什么?
说明钟钮左右两端转动180°后完全重合,两端均在以轴心为圆心的圆上运动,说明圆是中心对称图形,对称中心是圆心。
归纳概括
活动1
结论:
1.圆是轴对称图形,其对称轴是任意一条过圆心的直线。
2.圆是中心对称图形,对称中心为圆心。
探究一:圆的中心对称性
想一想:由以上现象,概括圆的对称性。
大胆操作 探究新知识
活动1
探究二:圆心角、弧、弦之间的关系
1.按下面的步骤做一做:
(1)在两张透明纸上,作两个半径相等的⊙O和⊙O′,沿圆周分别将两圆剪下;
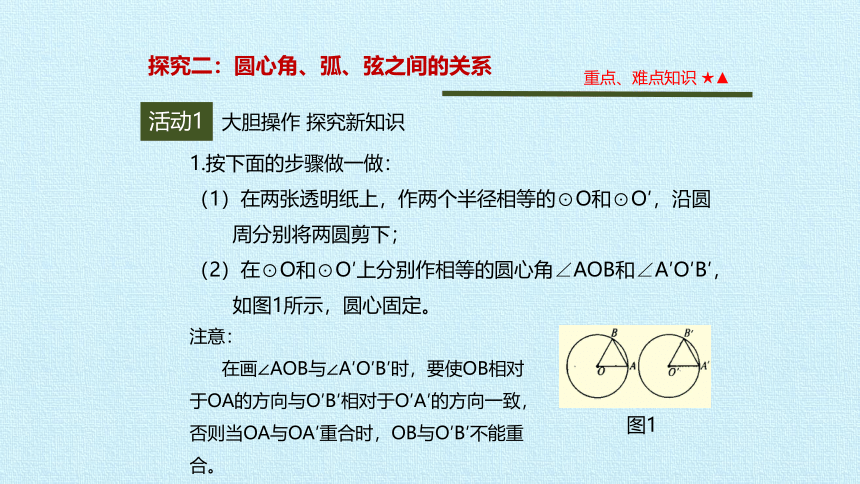
(2)在⊙O和⊙O′上分别作相等的圆心角∠AOB和∠A′O′B′,如图1所示,圆心固定。
重点、难点知识 ★▲
图1
注意:
在画∠AOB与∠A′O′B′时,要使OB相对于OA的方向与O′B′相对于O′A′的方向一致,否则当OA与OA′重合时,OB与O′B′不能重合。
大胆操作 探究新知识
活动1
探究二:圆心角、弧、弦之间的关系
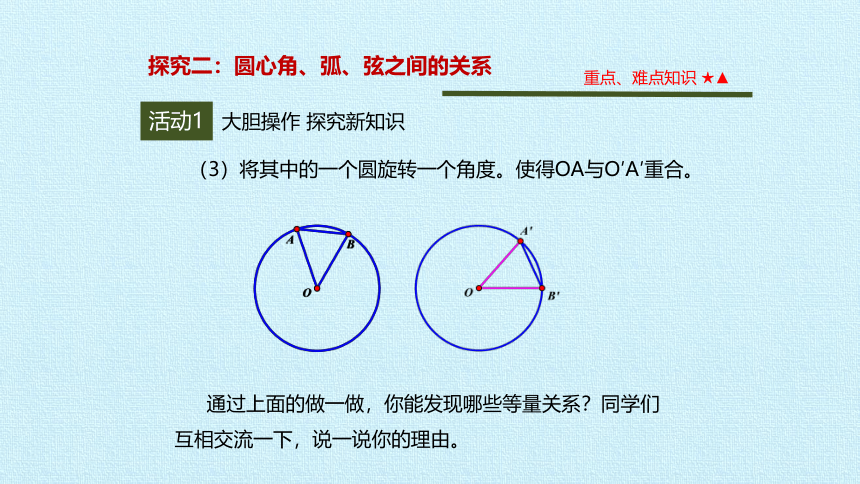
(3)将其中的一个圆旋转一个角度。使得OA与O′A′重合。
重点、难点知识 ★▲
通过上面的做一做,你能发现哪些等量关系?同学们互相交流一下,说一说你的理由。
活动1
探究二:圆心角、弧、弦之间的关系
重点、难点知识 ★▲
图1
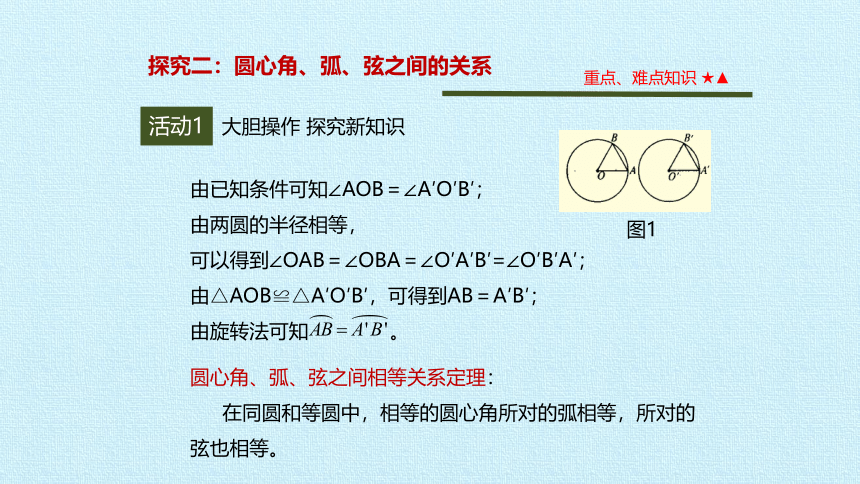
由已知条件可知∠AOB=∠A′O′B′;
由两圆的半径相等,
可以得到∠OAB=∠OBA=∠O′A′B′=∠O′B′A′;
由△AOB≌△A′O′B′,可得到AB=A′B′;
由旋转法可知 。
大胆操作 探究新知识
圆心角、弧、弦之间相等关系定理:
在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
集思广益 证明新知
活动2
探究二:圆心角、弧、弦之间的关系
重点、难点知识 ★▲
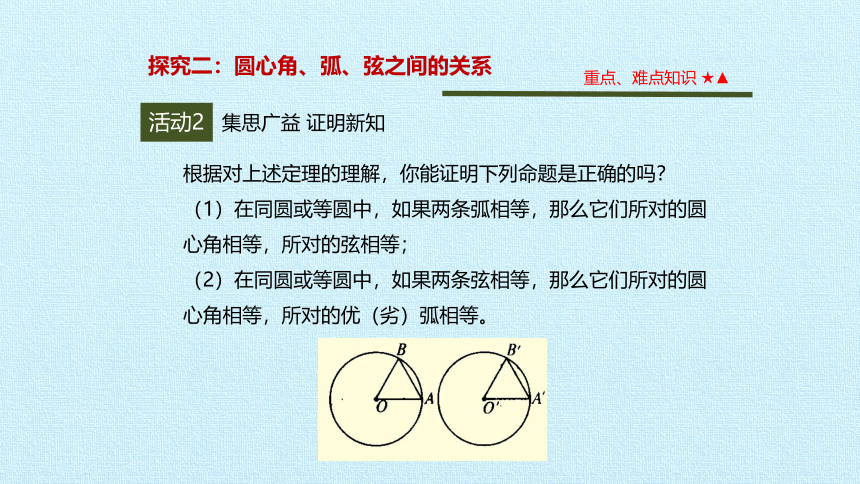
根据对上述定理的理解,你能证明下列命题是正确的吗?
(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;
(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优(劣)弧相等。
反思过程,发现定理。
活动3
探究二:圆心角、弧、弦之间的关系
重点、难点知识 ★▲
定理“在同圆和等圆中, 相等的圆心角所对的弧相等, 所对的弦也相等”中, 可否把条件“在同圆或等圆中”去掉?为什么?
如图,虽然∠AOB=∠A′O′B′,但AB≠A′B′, 。
反思过程,发现定理。
活动3
探究二:圆心角、弧、弦之间的关系
重点、难点知识 ★▲
思考:(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优(劣)弧相等中的条件“在同圆和等圆中”是否能够去掉?
弦、圆心角、弧三量关系:
在同圆或者等圆中,圆心角,弧,弦有一个量相等,那么其他的量也对应相等。
旧题新解
活动1
探究三:圆心角、弧、弦之间关系定理的应用
【思路点拨】对开放性逆向思维的题目,首先应依题意抓住问题适合的依据定理,再由定理和题设补充条件。
例1.如图, 的直径CD与弦AB交于点M,添加条件 (写出一个即可),就可得到M是AB的中点。
练习:如上图,CD是 的直径,AB是弦,CD⊥AB于M,则可得出AM=MB, 等多个结论,请你按现有图形给出其他两个结论。
集思广益 求解角度
活动2
探究三:圆心角、弧、弦之间关系定理的应用
例2.如图,在⊙O中, ,∠ACB=60°,求证∠AOB=∠AOC=∠BOC。
【思路点拨】由 ,有AB=AC,可得△ABC是等边三角形,故AB=AC=BC,所以得∠AOB=∠AOC=∠BOC。
证明:∵
∴ AB=AC,△ABC是等腰三角形。
又 ∠ACB=60°,
∴ △ABC是等边三角形,AB=BC=CA。
∴ ∠AOB=∠AOC=∠BOC。
集思广益 求解角度
活动2
探究三:圆心角、弧、弦之间关系定理的应用
练习:如图,AB是⊙O的直径,BC、CD、DA是⊙O的弦,且BC=CD=DA,求∠BOD的度数。
【思路点拨】求圆心角度数,可先求出该圆心角度数所对弧的度数。
解:由BC=CD=DA可以得到这三条弦所对的圆心角相等,
连接OC,得到∠AOD=∠DOC=∠BOC,
∵AB是直径,
∴∠BOD= ×180°=120°
大胆探索,证明线段相等与弧度相等。
活动3
探究三:圆心角、弧、弦之间关系定理的应用
例3.如图,AB,CD是⊙O的弦,M、N分别为AB、CD的中点且∠AMN=∠CNM,求证:AB=CD。
【思路点拨】
由中点想到垂径定理,由等角对等边定理可以得到线段与角度的相等关系,可以为证明全等三角形创造条件。
大胆探索,证明线段相等与弧度相等。
活动3
探究三:圆心角、弧、弦之间关系定理的应用
证明:∵M、N为AB,CD中点,
∴OM⊥AB,ON⊥CD。
∵ ∠AMN=∠CNM,
∴ ∠OMN=∠ONM。
∴OM=ON。
连接OB、OD,则OB=OD,
∴Rt△OMB≌Rt△OND。
∴BM=DN,
∴AB=CD。
大胆探索,证明线段相等与弧度相等。
活动3
探究三:圆心角、弧、弦之间关系定理的应用
【思路点拨】
由圆心角、弧、弦之间关系定理可以得到线段与角度的相等关系,可以为证明全等三角形创造条件。
练习:如图,AB是⊙O的直径 , P、Q是AB上两点, 且AP=BQ , C、D是⊙O上两点,且 ,分别延长CP、DQ,交⊙O于M、N,求证:CP=DQ。
大胆探索,证明线段相等与弧度相等。
活动3
探究三:圆心角、弧、弦之间关系定理的应用
证明:连接AC,BD,CO,DO,
∵ ,
∴ AC=BD,∠COA=∠DOB
∵AP=BQ ,
∴△ACP≌△BDQ ,
∴CP=DQ 。
(1)圆心角概念:顶点在圆心的角叫圆心角。
(2)圆是轴对称图形,也是中心对称图形。
(3)在同圆或者等圆中,圆心角、弦、弧中有一个量的相等,就可以推出其他两个量对应相等。
(1)在同圆或者等圆中,圆心角、弦、弧中有一个量的相等,就可以推出其他两个量对应相等。
(2)圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件不可忽略。
(3)由圆心角、弧、弦之间关系定理可以求得圆中的角度,证明圆中的线段和弧相等。
谢 谢
(1)圆是轴对称图形,其对称轴是任意一条过圆心的直线。
(2)垂直于弦的直径平分弦,并且平分弦所对的弧。
(3)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
以旧引新
活动1
现象一:一块圆形的蛋糕,糕点师只要过圆心点在互相垂直的两个方向上切两刀,不管糕点师站在哪里,分成的四块一定是均等的。 这个现象跟圆的哪个性质有关?
探究一:圆的中心对称性
想一想:这些现象说明了什么?
说明对折后能够完全重合,只要是过圆心的直线,分成的两部分均对称,说明圆是轴对称图形,对称轴是过圆心的任一条直线。
以旧引新
活动1
现象二:机械式闹钟上钟时,每次只要转动发条上的钟钮 180°时,看上去跟没转动以前是一个样的。这个现象跟圆的哪个性质有关?
探究一:圆的中心对称性
想一想:这些现象说明了什么?
说明钟钮左右两端转动180°后完全重合,两端均在以轴心为圆心的圆上运动,说明圆是中心对称图形,对称中心是圆心。
归纳概括
活动1
结论:
1.圆是轴对称图形,其对称轴是任意一条过圆心的直线。
2.圆是中心对称图形,对称中心为圆心。
探究一:圆的中心对称性
想一想:由以上现象,概括圆的对称性。
大胆操作 探究新知识
活动1
探究二:圆心角、弧、弦之间的关系
1.按下面的步骤做一做:
(1)在两张透明纸上,作两个半径相等的⊙O和⊙O′,沿圆周分别将两圆剪下;
(2)在⊙O和⊙O′上分别作相等的圆心角∠AOB和∠A′O′B′,如图1所示,圆心固定。
重点、难点知识 ★▲
图1
注意:
在画∠AOB与∠A′O′B′时,要使OB相对于OA的方向与O′B′相对于O′A′的方向一致,否则当OA与OA′重合时,OB与O′B′不能重合。
大胆操作 探究新知识
活动1
探究二:圆心角、弧、弦之间的关系
(3)将其中的一个圆旋转一个角度。使得OA与O′A′重合。
重点、难点知识 ★▲
通过上面的做一做,你能发现哪些等量关系?同学们互相交流一下,说一说你的理由。
活动1
探究二:圆心角、弧、弦之间的关系
重点、难点知识 ★▲
图1
由已知条件可知∠AOB=∠A′O′B′;
由两圆的半径相等,
可以得到∠OAB=∠OBA=∠O′A′B′=∠O′B′A′;
由△AOB≌△A′O′B′,可得到AB=A′B′;
由旋转法可知 。
大胆操作 探究新知识
圆心角、弧、弦之间相等关系定理:
在同圆和等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
集思广益 证明新知
活动2
探究二:圆心角、弧、弦之间的关系
重点、难点知识 ★▲
根据对上述定理的理解,你能证明下列命题是正确的吗?
(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;
(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优(劣)弧相等。
反思过程,发现定理。
活动3
探究二:圆心角、弧、弦之间的关系
重点、难点知识 ★▲
定理“在同圆和等圆中, 相等的圆心角所对的弧相等, 所对的弦也相等”中, 可否把条件“在同圆或等圆中”去掉?为什么?
如图,虽然∠AOB=∠A′O′B′,但AB≠A′B′, 。
反思过程,发现定理。
活动3
探究二:圆心角、弧、弦之间的关系
重点、难点知识 ★▲
思考:(1)在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等;(2)在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的优(劣)弧相等中的条件“在同圆和等圆中”是否能够去掉?
弦、圆心角、弧三量关系:
在同圆或者等圆中,圆心角,弧,弦有一个量相等,那么其他的量也对应相等。
旧题新解
活动1
探究三:圆心角、弧、弦之间关系定理的应用
【思路点拨】对开放性逆向思维的题目,首先应依题意抓住问题适合的依据定理,再由定理和题设补充条件。
例1.如图, 的直径CD与弦AB交于点M,添加条件 (写出一个即可),就可得到M是AB的中点。
练习:如上图,CD是 的直径,AB是弦,CD⊥AB于M,则可得出AM=MB, 等多个结论,请你按现有图形给出其他两个结论。
集思广益 求解角度
活动2
探究三:圆心角、弧、弦之间关系定理的应用
例2.如图,在⊙O中, ,∠ACB=60°,求证∠AOB=∠AOC=∠BOC。
【思路点拨】由 ,有AB=AC,可得△ABC是等边三角形,故AB=AC=BC,所以得∠AOB=∠AOC=∠BOC。
证明:∵
∴ AB=AC,△ABC是等腰三角形。
又 ∠ACB=60°,
∴ △ABC是等边三角形,AB=BC=CA。
∴ ∠AOB=∠AOC=∠BOC。
集思广益 求解角度
活动2
探究三:圆心角、弧、弦之间关系定理的应用
练习:如图,AB是⊙O的直径,BC、CD、DA是⊙O的弦,且BC=CD=DA,求∠BOD的度数。
【思路点拨】求圆心角度数,可先求出该圆心角度数所对弧的度数。
解:由BC=CD=DA可以得到这三条弦所对的圆心角相等,
连接OC,得到∠AOD=∠DOC=∠BOC,
∵AB是直径,
∴∠BOD= ×180°=120°
大胆探索,证明线段相等与弧度相等。
活动3
探究三:圆心角、弧、弦之间关系定理的应用
例3.如图,AB,CD是⊙O的弦,M、N分别为AB、CD的中点且∠AMN=∠CNM,求证:AB=CD。
【思路点拨】
由中点想到垂径定理,由等角对等边定理可以得到线段与角度的相等关系,可以为证明全等三角形创造条件。
大胆探索,证明线段相等与弧度相等。
活动3
探究三:圆心角、弧、弦之间关系定理的应用
证明:∵M、N为AB,CD中点,
∴OM⊥AB,ON⊥CD。
∵ ∠AMN=∠CNM,
∴ ∠OMN=∠ONM。
∴OM=ON。
连接OB、OD,则OB=OD,
∴Rt△OMB≌Rt△OND。
∴BM=DN,
∴AB=CD。
大胆探索,证明线段相等与弧度相等。
活动3
探究三:圆心角、弧、弦之间关系定理的应用
【思路点拨】
由圆心角、弧、弦之间关系定理可以得到线段与角度的相等关系,可以为证明全等三角形创造条件。
练习:如图,AB是⊙O的直径 , P、Q是AB上两点, 且AP=BQ , C、D是⊙O上两点,且 ,分别延长CP、DQ,交⊙O于M、N,求证:CP=DQ。
大胆探索,证明线段相等与弧度相等。
活动3
探究三:圆心角、弧、弦之间关系定理的应用
证明:连接AC,BD,CO,DO,
∵ ,
∴ AC=BD,∠COA=∠DOB
∵AP=BQ ,
∴△ACP≌△BDQ ,
∴CP=DQ 。
(1)圆心角概念:顶点在圆心的角叫圆心角。
(2)圆是轴对称图形,也是中心对称图形。
(3)在同圆或者等圆中,圆心角、弦、弧中有一个量的相等,就可以推出其他两个量对应相等。
(1)在同圆或者等圆中,圆心角、弦、弧中有一个量的相等,就可以推出其他两个量对应相等。
(2)圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件不可忽略。
(3)由圆心角、弧、弦之间关系定理可以求得圆中的角度,证明圆中的线段和弧相等。
谢 谢
同课章节目录
