人教版数学九年级上册:24.1.4圆周角课件(共18张PPT)
文档属性
| 名称 | 人教版数学九年级上册:24.1.4圆周角课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 324.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 00:00:00 | ||
图片预览




文档简介
24.1.4 圆周角
新人教版九年级上册
1、什么叫圆心角?
.
O
A
B
顶点在圆心的角叫圆心角。
2、 圆心角、弧、弦三个量之
间的关系有一个结论,这个结论是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
查学诊断
示标导入
1、了解圆周角的概念。
2、理解圆周角的定理。
.
O
A
问题:将圆心角顶点向上移,直至与⊙O相交于点C?观察得到的∠ACB有什么特征?
C
B
导学施教:情境引入
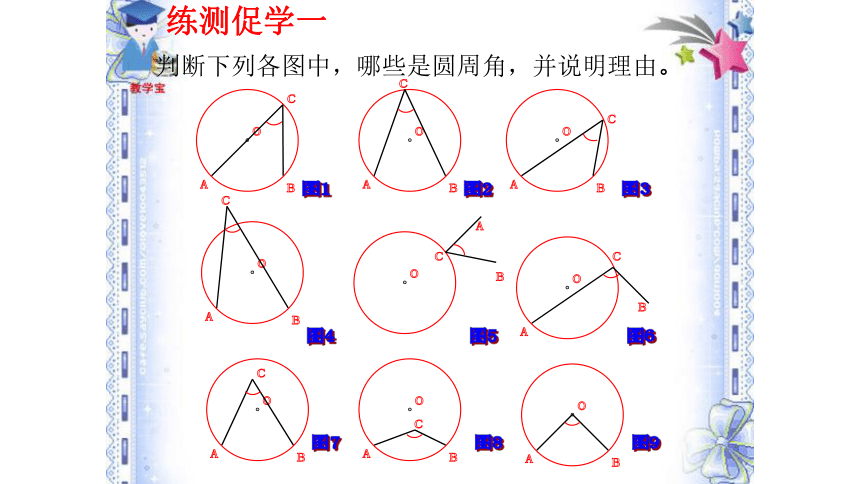
定义:顶点在圆上,两边都和圆相交的角叫做圆周角。
圆周角的特征:①顶点在圆上;
②两边都和圆相交。
判断下列各图中,哪些是圆周角,并说明理由。
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
C
C
C
C
C
C
C
C
图1
图2
图3
图4
图5
图6
图7
图8
图9
练测促学一
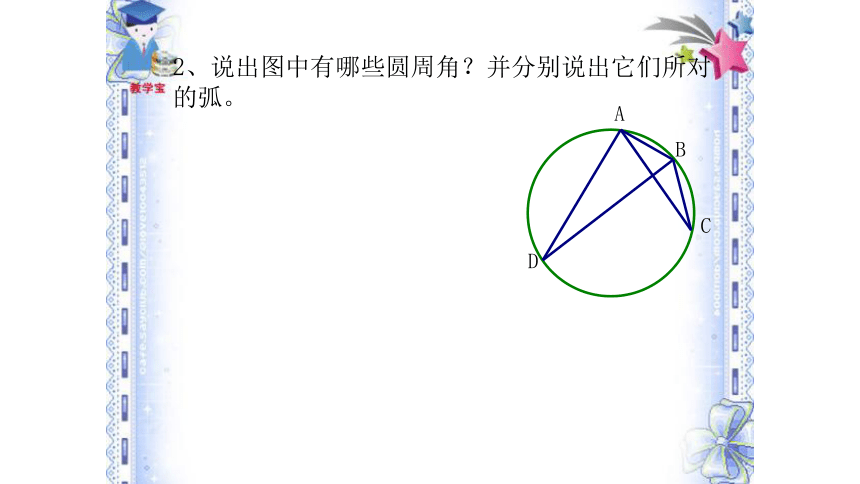
2、说出图中有哪些圆周角?并分别说出它们所对的弧。
A
B
C
D
1、请在⊙O中画出 所对的圆心角和圆周角,
你能画出多少个符合条件的圆心角和圆周角?
O
B
C
(
BC
自主探究
2、 所对的圆周角有无数个,观察你所画的图形,它们与圆心O有哪几种位置关系?
O在∠BAC内
O在∠BAC边上
O在∠BAC外
(
BC
3、当圆心O在∠BAC的一边上时,圆周角∠BAC
与圆心角∠BOC之间有怎样的数量关系?你能证明
你的发现吗?
∵∠BOC是△AOC的外角,
∴∠BOC=∠A +∠C.
∵OA=OC ,
∴∠C=∠A .
∴∠BOC=2∠A .
即
证明:
.
.
5.当圆心O在∠BAC的内部或外部时,
的关系还成立吗?
,
证明:作直径AD.
.
∵
,
∴
即
.
,
证明:作直径AD.
即
.
∵
,
.
∴
综上所述,圆周角∠BAC与圆心角∠BOC的大小关系是:
即 ∠BAC = ∠BOC.
一条弧所对的圆周角等于它所对的圆心角的一半。
例1 如图,⊙O的弦AB、DC的延长线相交于点E,∠AOD=150°,BD=BE,求∠ABD、∠AED的度数.
例题解析
1、变式一:如果∠A=44°,则∠BOC=____,
∠OBC 。
变式二:如果∠BOC=44°,则∠A=____。
变式三:如果BC的度数是44°,那么这
条弧所对的圆心角和圆周角分别等于
, 。
变式四:n°弧所对的圆心角是 ,所对的圆周角是 。
O
A
B
C
2、 在⊙O中,一条弧所对的圆心角和圆周角分别(2x+100)°和 (5x—30)°,求这条弧所对的圆心角和圆周角的度数。
练测促学二
⌒
3、一条弦分圆为1:4两部分,求这弦所对的圆周角的度数?
88°
46°
22°
44°
22°
n°
n°
小结:通过这节课的学习你的收获是什么?
拓展延伸
布置作业:P89 2
同步练习册
新人教版九年级上册
1、什么叫圆心角?
.
O
A
B
顶点在圆心的角叫圆心角。
2、 圆心角、弧、弦三个量之
间的关系有一个结论,这个结论是什么?
在同圆(或等圆)中,如果圆心角、弧、弦有一组量相等,那么它们所对应的其余两个量都分别相等。
查学诊断
示标导入
1、了解圆周角的概念。
2、理解圆周角的定理。
.
O
A
问题:将圆心角顶点向上移,直至与⊙O相交于点C?观察得到的∠ACB有什么特征?
C
B
导学施教:情境引入
定义:顶点在圆上,两边都和圆相交的角叫做圆周角。
圆周角的特征:①顶点在圆上;
②两边都和圆相交。
判断下列各图中,哪些是圆周角,并说明理由。
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
C
C
C
C
C
C
C
C
图1
图2
图3
图4
图5
图6
图7
图8
图9
练测促学一
2、说出图中有哪些圆周角?并分别说出它们所对的弧。
A
B
C
D
1、请在⊙O中画出 所对的圆心角和圆周角,
你能画出多少个符合条件的圆心角和圆周角?
O
B
C
(
BC
自主探究
2、 所对的圆周角有无数个,观察你所画的图形,它们与圆心O有哪几种位置关系?
O在∠BAC内
O在∠BAC边上
O在∠BAC外
(
BC
3、当圆心O在∠BAC的一边上时,圆周角∠BAC
与圆心角∠BOC之间有怎样的数量关系?你能证明
你的发现吗?
∵∠BOC是△AOC的外角,
∴∠BOC=∠A +∠C.
∵OA=OC ,
∴∠C=∠A .
∴∠BOC=2∠A .
即
证明:
.
.
5.当圆心O在∠BAC的内部或外部时,
的关系还成立吗?
,
证明:作直径AD.
.
∵
,
∴
即
.
,
证明:作直径AD.
即
.
∵
,
.
∴
综上所述,圆周角∠BAC与圆心角∠BOC的大小关系是:
即 ∠BAC = ∠BOC.
一条弧所对的圆周角等于它所对的圆心角的一半。
例1 如图,⊙O的弦AB、DC的延长线相交于点E,∠AOD=150°,BD=BE,求∠ABD、∠AED的度数.
例题解析
1、变式一:如果∠A=44°,则∠BOC=____,
∠OBC 。
变式二:如果∠BOC=44°,则∠A=____。
变式三:如果BC的度数是44°,那么这
条弧所对的圆心角和圆周角分别等于
, 。
变式四:n°弧所对的圆心角是 ,所对的圆周角是 。
O
A
B
C
2、 在⊙O中,一条弧所对的圆心角和圆周角分别(2x+100)°和 (5x—30)°,求这条弧所对的圆心角和圆周角的度数。
练测促学二
⌒
3、一条弦分圆为1:4两部分,求这弦所对的圆周角的度数?
88°
46°
22°
44°
22°
n°
n°
小结:通过这节课的学习你的收获是什么?
拓展延伸
布置作业:P89 2
同步练习册
同课章节目录
