人教版数学九年级上册:24.2.1《点和圆的位置关系》 课件(共27张PPT)
文档属性
| 名称 | 人教版数学九年级上册:24.2.1《点和圆的位置关系》 课件(共27张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 417.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
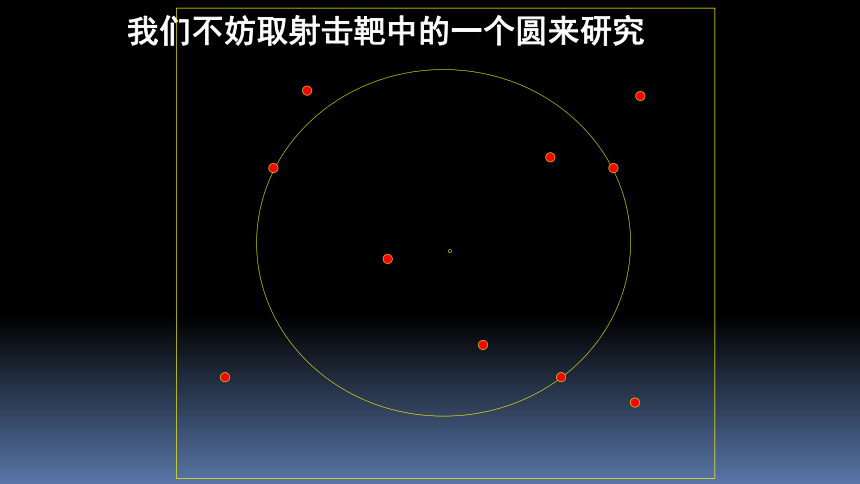
我国射击运动员杜丽在雅典奥运会上获得了首金,为我国赢得了荣誉。如图是射击靶的示意图,它是由许多同心圆构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
观 察
24.2.1 点和圆的位置关系
1.理解并掌握,设⊙O的半径为r,点P到圆心的距离OP=d,则有:点P在圆外d>r;点P在圆上d=r;点P在圆内d2.理解不在同一直线上的三个点确定一个圆并掌握它的运用.了解三角形的外接圆和三角形外心的概念.
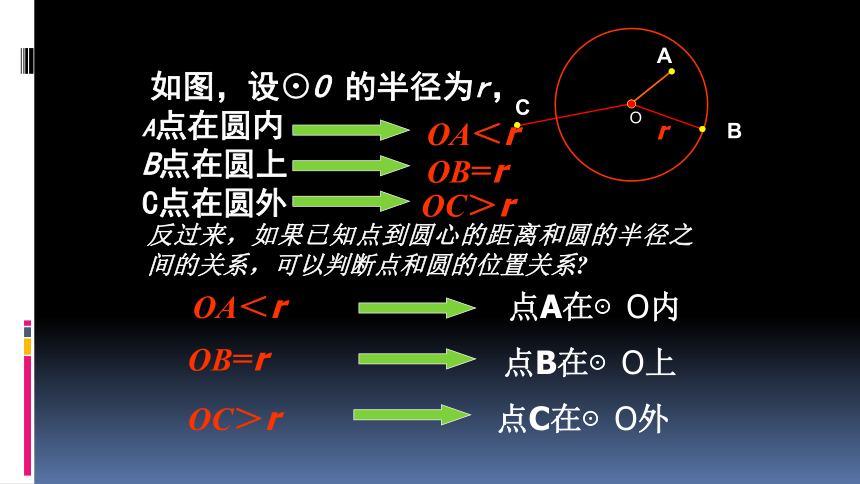
我们不妨取射击靶中的一个圆来研究
1、点和圆的位置关系有三种:
点在圆内、点在圆上、点在圆外
2、如何用数量关系来表示图中的点与圆的位置关系呢?小组合作交流完成。
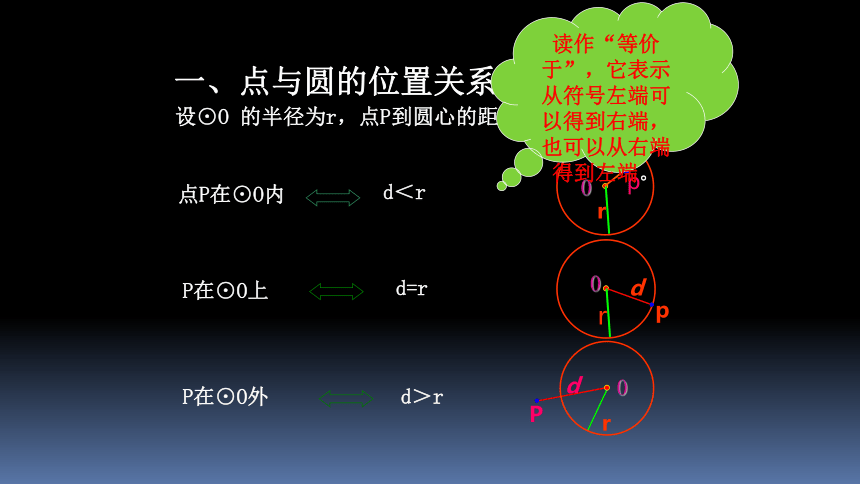
如图,设⊙O 的半径为r,
A点在圆内
B点在圆上
C点在圆外
点A在⊙O内
点B在⊙O上
点C在⊙O外
反过来,如果已知点到圆心的距离和圆的半径之间的关系,可以判断点和圆的位置关系
OA<r
OB=r
OC>r
A
B
C
r
OA<r
OB=r
OC>r
O
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
P在⊙O上
P在⊙O外
d<r
d=r
d>r
一、点与圆的位置关系
r
d
0
p
r
d
0
P
r
d
0
p
读作“等价于”,它表示从符号左端可以得到右端,也可以从右端得到左端。
我国射击运动员杜丽在雅典奥运会上获得了首金,为我国赢得了荣誉。如图是射击靶的示意图,它是由许多同心圆构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
观 察
练习: ⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在_____;点B在_____ ;点C在________ .
圆内
圆上
圆外
●A
●A
●B
过一点可作几条直线?过两点可以作几条直线?过三点呢?
过两点有且只有一条直线(直线公理)
(“有且只有”就是“确定”的意思)
经过一点可以作无数条直线;
回忆思考:
过三点
1、若三点共线,则过这三点只能作一条直线.
A
B
C
2、若三点不共线,则过这三点不能作直线,但过任意其中两点一共可作三条直线.
A
B
C
直线公理:两点确定一条直线
画圆的关键是什么?
确定半径
回 顾
确定圆心
1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
探究与实践
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点?
无数个。它们的圆心都在线段AB的垂直平分线上。
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
●O
● O
●O
●O
B
A
A
B
C
为什么过同一直线上的三点不能作圆呢?
因为DE∥FG,所以没有交点,
即没有过这三点的圆心
D
F
E
G
过三点能作几个圆
1.三点共线
(不能作圆)
3. 过不在同一条直线上的三点可以作几个圆
A
B
C
经过A、B两点的圆的圆心在线段AB的垂直平分线上.
分析
A
B
C
步骤1
经过B、C两点的圆的圆心在线段BC的垂直平分线上.
A
B
C
步骤2
经过A、B、C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
A
B
C
步骤3
圆的内接三角形
三角形的外接圆
三角形的外心
A
B
C
O
外心
1。三边垂直平分线的交点
2。到三个顶点距离相等
过已知一点可作无数个圆.
过已知两点也可作无数个圆.
过不在同一条直线上的三点可以作一个圆,并且只能作一个圆.
二、知识要点
归纳结论:
不在同一条直线上的三个点确定一个圆。
随堂练习
1. 判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆 ( )
(2)任意一个圆有且只有一个内接三角形 ( )
(3)经过三点一定可以确定一个圆 ( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
√
×
课堂小结
点A在圆外
点B在圆上
点C在圆内
d < r
d = r
d > r
1. 点和圆的位置关系
A
B
C
r
r
r
d
d
d
过已知一点可作无数个圆.
过已知两点也可作无数个圆.
过不在同一条直线上的三点可以作一个圆,并且只能作一个圆.
2. 三点定圆
A
B
C
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,这个三角形叫这个圆的内接三角形.
外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心.
3. 外接圆、内接三角形
4. 外心
A
B
C
同步练习册:46页1、2、4、7、8
课堂检测
作业布置
A组同学做能力培养与测试 课时作业1-9
B组同学做能力培养与测试 课时作业1-6
我国射击运动员杜丽在雅典奥运会上获得了首金,为我国赢得了荣誉。如图是射击靶的示意图,它是由许多同心圆构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
观 察
24.2.1 点和圆的位置关系
1.理解并掌握,设⊙O的半径为r,点P到圆心的距离OP=d,则有:点P在圆外d>r;点P在圆上d=r;点P在圆内d
我们不妨取射击靶中的一个圆来研究
1、点和圆的位置关系有三种:
点在圆内、点在圆上、点在圆外
2、如何用数量关系来表示图中的点与圆的位置关系呢?小组合作交流完成。
如图,设⊙O 的半径为r,
A点在圆内
B点在圆上
C点在圆外
点A在⊙O内
点B在⊙O上
点C在⊙O外
反过来,如果已知点到圆心的距离和圆的半径之间的关系,可以判断点和圆的位置关系
OA<r
OB=r
OC>r
A
B
C
r
OA<r
OB=r
OC>r
O
设⊙O 的半径为r,点P到圆心的距离OP=d,则有:
点P在⊙O内
P在⊙O上
P在⊙O外
d<r
d=r
d>r
一、点与圆的位置关系
r
d
0
p
r
d
0
P
r
d
0
p
读作“等价于”,它表示从符号左端可以得到右端,也可以从右端得到左端。
我国射击运动员杜丽在雅典奥运会上获得了首金,为我国赢得了荣誉。如图是射击靶的示意图,它是由许多同心圆构成的,你知道击中靶上不同位置的成绩是如何计算的吗?
观 察
练习: ⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在_____;点B在_____ ;点C在________ .
圆内
圆上
圆外
●A
●A
●B
过一点可作几条直线?过两点可以作几条直线?过三点呢?
过两点有且只有一条直线(直线公理)
(“有且只有”就是“确定”的意思)
经过一点可以作无数条直线;
回忆思考:
过三点
1、若三点共线,则过这三点只能作一条直线.
A
B
C
2、若三点不共线,则过这三点不能作直线,但过任意其中两点一共可作三条直线.
A
B
C
直线公理:两点确定一条直线
画圆的关键是什么?
确定半径
回 顾
确定圆心
1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
探究与实践
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点?
无数个。它们的圆心都在线段AB的垂直平分线上。
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
●O
● O
●O
●O
B
A
A
B
C
为什么过同一直线上的三点不能作圆呢?
因为DE∥FG,所以没有交点,
即没有过这三点的圆心
D
F
E
G
过三点能作几个圆
1.三点共线
(不能作圆)
3. 过不在同一条直线上的三点可以作几个圆
A
B
C
经过A、B两点的圆的圆心在线段AB的垂直平分线上.
分析
A
B
C
步骤1
经过B、C两点的圆的圆心在线段BC的垂直平分线上.
A
B
C
步骤2
经过A、B、C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
A
B
C
步骤3
圆的内接三角形
三角形的外接圆
三角形的外心
A
B
C
O
外心
1。三边垂直平分线的交点
2。到三个顶点距离相等
过已知一点可作无数个圆.
过已知两点也可作无数个圆.
过不在同一条直线上的三点可以作一个圆,并且只能作一个圆.
二、知识要点
归纳结论:
不在同一条直线上的三个点确定一个圆。
随堂练习
1. 判断下列说法是否正确
(1)任意的一个三角形一定有一个外接圆 ( )
(2)任意一个圆有且只有一个内接三角形 ( )
(3)经过三点一定可以确定一个圆 ( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
√
×
课堂小结
点A在圆外
点B在圆上
点C在圆内
d < r
d = r
d > r
1. 点和圆的位置关系
A
B
C
r
r
r
d
d
d
过已知一点可作无数个圆.
过已知两点也可作无数个圆.
过不在同一条直线上的三点可以作一个圆,并且只能作一个圆.
2. 三点定圆
A
B
C
经过三角形的三个顶点可以作一个圆,这个圆叫做三角形的外接圆,这个三角形叫这个圆的内接三角形.
外接圆的圆心是三角形三边垂直平分线的交点,叫做三角形的外心.
3. 外接圆、内接三角形
4. 外心
A
B
C
同步练习册:46页1、2、4、7、8
课堂检测
作业布置
A组同学做能力培养与测试 课时作业1-9
B组同学做能力培养与测试 课时作业1-6
同课章节目录
