24.2.2直线和圆的位置(第2课时).课件
文档属性
| 名称 | 24.2.2直线和圆的位置(第2课时).课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-19 19:55:03 | ||
图片预览




文档简介
(共22张PPT)
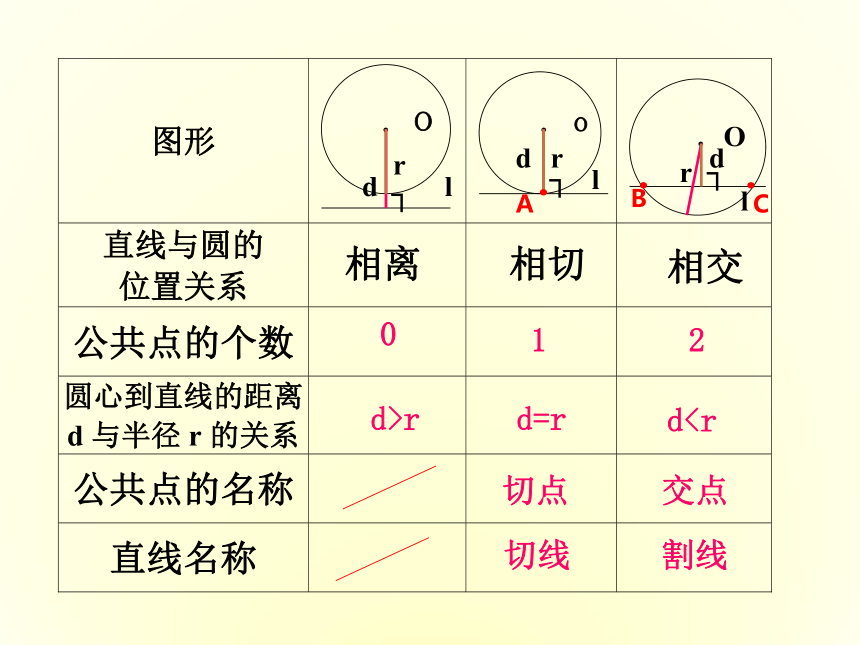
0
d>r
1
d=r
切点
切线
2
d交点
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
问题1:下雨天,转动的雨伞上的水滴是顺着伞的什么方向飞出去的
问题2:砂轮转动时,火花是沿着砂轮的什么方向飞出去的
●O
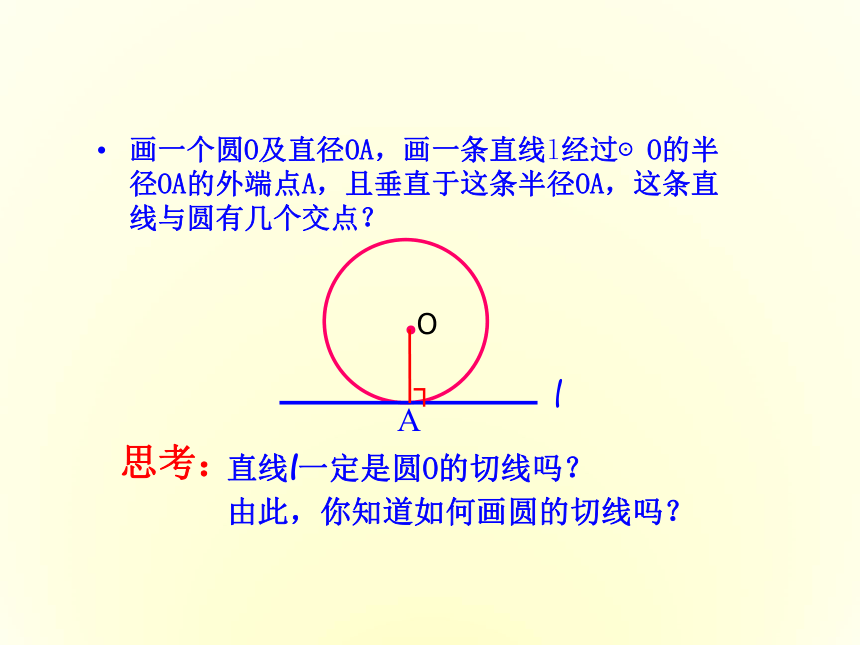
画一个圆O及直径OA,画一条直线l经过⊙O的半径OA的外端点A,且垂直于这条半径OA,这条直线与圆有几个交点?
┐
A
l
直线l一定是圆O的切线吗?
由此,你知道如何画圆的切线吗?
思考:
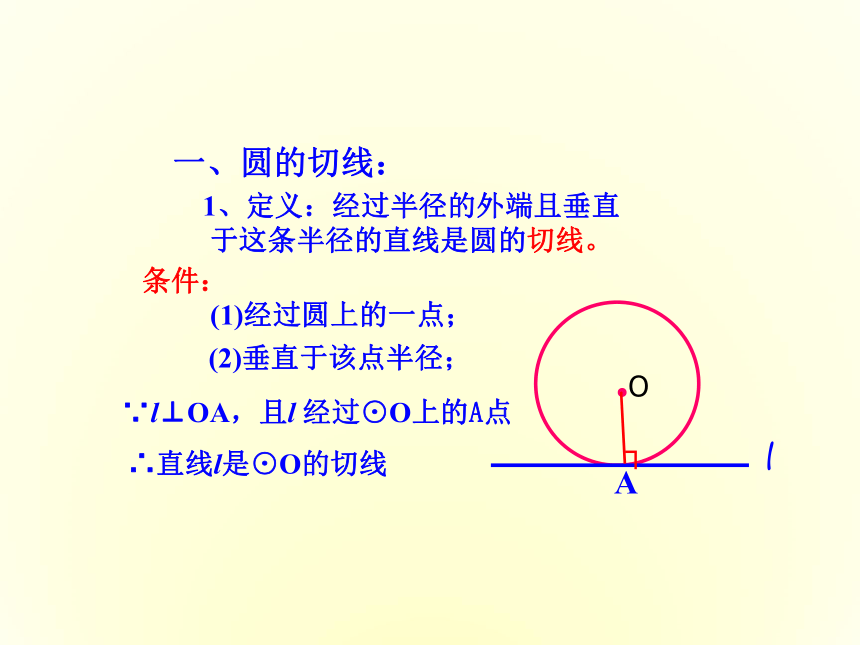
1、定义:经过半径的外端且垂直于这条半径的直线是圆的切线。
条件:
(1)经过圆上的一点;
一、圆的切线:
(2)垂直于该点半径;
∵l⊥OA,且l 经过⊙O上的A点
∴直线l是⊙O的切线
●O
┐
A
l
切线的判定定理:
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.
2、对定理的理解:
一条直线是圆的切线需满足两条:
②垂直于这条半径.
注意:定理中的两个条件缺一不可.
①经过半径外端.
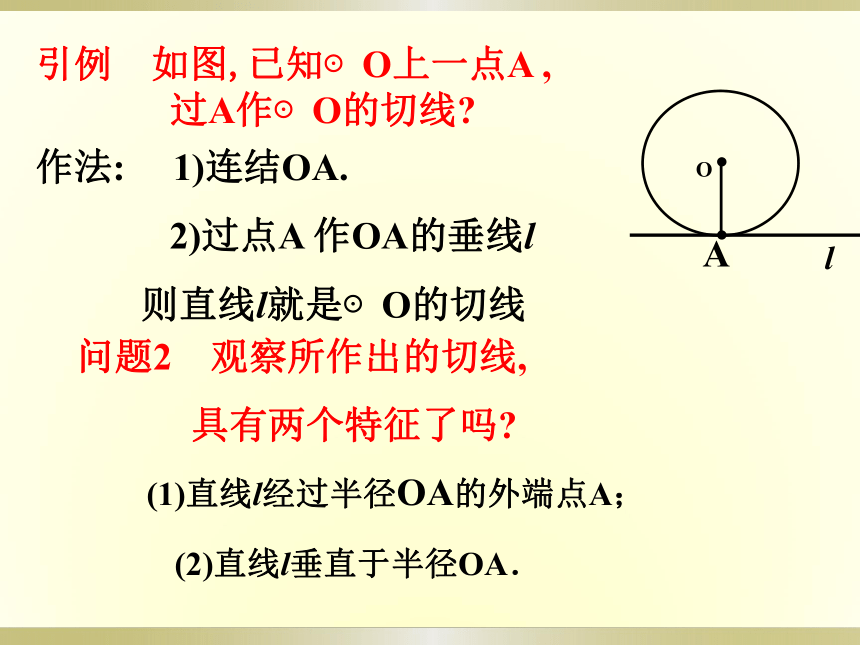
引例 如图,已知⊙O上一点A ,
过A作⊙O的切线
(1)直线l经过半径OA的外端点A;
(2)直线l垂直于半径OA.
问题2 观察所作出的切线,
具有两个特征了吗
O
A
l
作法: 1)连结OA.
2)过点A 作OA的垂线l
则直线l就是⊙O的切线
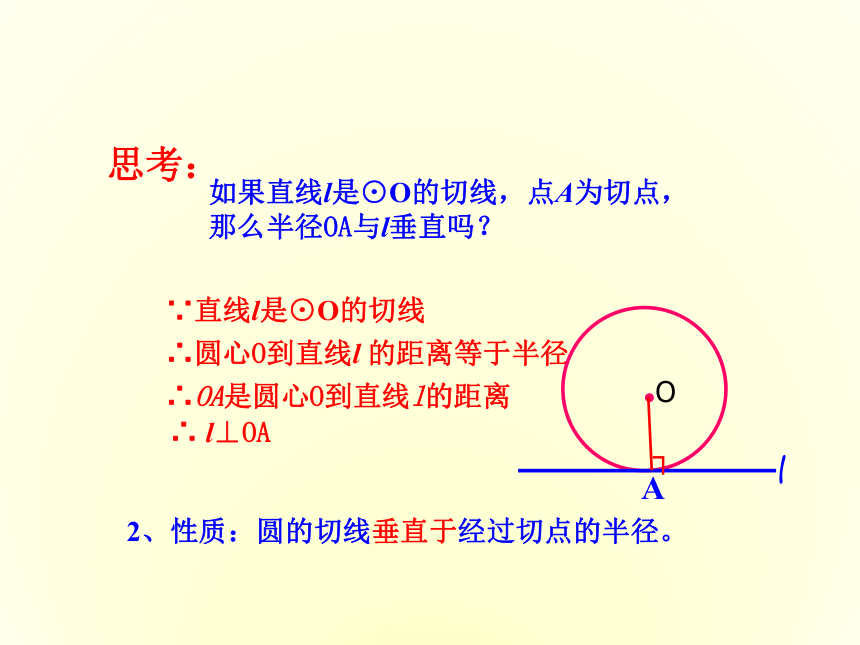
如果直线l是⊙O的切线,点A为切点,那么半径OA与l垂直吗?
∵直线l是⊙O的切线
思考:
2、性质:圆的切线垂直于经过切点的半径。
∴圆心O到直线l 的距离等于半径
∴OA是圆心O到直线l的距离
∴ l⊥OA
●O
┐
A
l
应用定理.
例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
直线AB经过半径0C的外端C,并且垂直于半径0C, 所以AB是⊙O的切线.
A
B
C
O
证明:连结0C
∵0A=0B,CA=CB,
∴0C是等腰三角形0AB底边AB上的中线.
∴AB⊥OC.
方法小结: 证明过圆上一点的直线是圆的切线.只要证明这条直线垂直于经过切点的半径.
例2.如图,AB是⊙O的直径,∠B=45°,AC=AB。
AC是⊙O的切线吗?为什么?
解:AC是⊙O的切线 。理由如下:
又∵∠BAC+∠B+∠C = 180°
∵ AC=AB , ∠B=45°(已知)
∴ 直线AC⊥AB
又∵直线AC经过⊙O 上的A点
∴直线AC是⊙O的切线
∴∠C=∠B=45°(等边对等角)
∴∠ BAC = 180°-∠B-∠C=90°
O
●
A
B
C
跟踪练习:如右图所示,已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?为什么?
解:直线AB是⊙O的切线 。理由如下:
在圆O 中,
又∵∠OAB+∠OBA+∠AOB = 180°
∵因为AB=OA,∠OBA=45°(已知)
∴∠AOB=∠OBA=45°(等边对等角)
∴∠OAB=180°-∠OBA-∠AOB=90°
∴ 直线AB⊥OA
又∵直线AB经过⊙O 上的A点
∴直线AB是⊙O的切线
A
B
O
●
例3.如图,O为∠PAQ的角平分线上的一点,OB⊥AP于点B,以O为圆心OB为半径作⊙B,
求证:AQ与⊙O相切
1.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
2、以三角形的一边为直径的圆恰好与另一边相切,则此三角形是__________三角形
直角
3、已知,如图在 中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C且 AD=DC则 ABD= 。
45
O
D
C
B
A
4.如图,⊙O的半径为3cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为 s时,BP与⊙O相切.
1或5
P1
5.如图, AB是⊙O的直径,∠B=45°,
AC=AB, AC是⊙O的切线吗?
为什么?
C
B
A
0
6.如图,在△ABC中 ∠ABC=90°,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED
求证:DE是⊙O的切线
·
O
A
C
B
E
D
7.如图,已知,AB是⊙O直径,BC⊥AB于B,⊙O的弦AD∥OC,
求证:DC是⊙O的切线.
D
O
B
C
A
8,如图,△ABC为等腰三角形,O为底边BC的中点,OD⊥AB,以O为圆心OD为半径作⊙O,
求证:AC与⊙O相切.
9.已知:如图, 梯形ABCD中,AD‖BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O.
求证:CD为⊙O的切线.
.
A
D
O
B
C
.
1、如何判定一条直线是已知圆的切线?
(1)和圆只有一个公共点的直线是圆的切线;
(2)和圆心的距离等于半径的直线是圆的切线;
(3)过半径外端且和半径垂直的直线是圆的切线;
(d=r)
1、经过圆上的一点;
2、 垂直于半径;
2、圆的切线有什么性质?
圆的切线垂直于经过切点的半径。
小结
0
d>r
1
d=r
切点
切线
2
d
割线
.O
l
d
r
┐
┐
.o
l
d
r
.O
l
d
┐
r
.
A
C
B
.
.
相离
相切
相交
问题1:下雨天,转动的雨伞上的水滴是顺着伞的什么方向飞出去的
问题2:砂轮转动时,火花是沿着砂轮的什么方向飞出去的
●O
画一个圆O及直径OA,画一条直线l经过⊙O的半径OA的外端点A,且垂直于这条半径OA,这条直线与圆有几个交点?
┐
A
l
直线l一定是圆O的切线吗?
由此,你知道如何画圆的切线吗?
思考:
1、定义:经过半径的外端且垂直于这条半径的直线是圆的切线。
条件:
(1)经过圆上的一点;
一、圆的切线:
(2)垂直于该点半径;
∵l⊥OA,且l 经过⊙O上的A点
∴直线l是⊙O的切线
●O
┐
A
l
切线的判定定理:
1、切线的判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.
2、对定理的理解:
一条直线是圆的切线需满足两条:
②垂直于这条半径.
注意:定理中的两个条件缺一不可.
①经过半径外端.
引例 如图,已知⊙O上一点A ,
过A作⊙O的切线
(1)直线l经过半径OA的外端点A;
(2)直线l垂直于半径OA.
问题2 观察所作出的切线,
具有两个特征了吗
O
A
l
作法: 1)连结OA.
2)过点A 作OA的垂线l
则直线l就是⊙O的切线
如果直线l是⊙O的切线,点A为切点,那么半径OA与l垂直吗?
∵直线l是⊙O的切线
思考:
2、性质:圆的切线垂直于经过切点的半径。
∴圆心O到直线l 的距离等于半径
∴OA是圆心O到直线l的距离
∴ l⊥OA
●O
┐
A
l
应用定理.
例1 已知:直线AB经过⊙O上的点C,
并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.
直线AB经过半径0C的外端C,并且垂直于半径0C, 所以AB是⊙O的切线.
A
B
C
O
证明:连结0C
∵0A=0B,CA=CB,
∴0C是等腰三角形0AB底边AB上的中线.
∴AB⊥OC.
方法小结: 证明过圆上一点的直线是圆的切线.只要证明这条直线垂直于经过切点的半径.
例2.如图,AB是⊙O的直径,∠B=45°,AC=AB。
AC是⊙O的切线吗?为什么?
解:AC是⊙O的切线 。理由如下:
又∵∠BAC+∠B+∠C = 180°
∵ AC=AB , ∠B=45°(已知)
∴ 直线AC⊥AB
又∵直线AC经过⊙O 上的A点
∴直线AC是⊙O的切线
∴∠C=∠B=45°(等边对等角)
∴∠ BAC = 180°-∠B-∠C=90°
O
●
A
B
C
跟踪练习:如右图所示,已知直线AB经过⊙O上的点A,且AB=OA,∠OBA=45°,直线AB是⊙O的切线吗?为什么?
解:直线AB是⊙O的切线 。理由如下:
在圆O 中,
又∵∠OAB+∠OBA+∠AOB = 180°
∵因为AB=OA,∠OBA=45°(已知)
∴∠AOB=∠OBA=45°(等边对等角)
∴∠OAB=180°-∠OBA-∠AOB=90°
∴ 直线AB⊥OA
又∵直线AB经过⊙O 上的A点
∴直线AB是⊙O的切线
A
B
O
●
例3.如图,O为∠PAQ的角平分线上的一点,OB⊥AP于点B,以O为圆心OB为半径作⊙B,
求证:AQ与⊙O相切
1.判断下列命题是否正确.
(1)经过半径外端的直线是圆的切线.( )
(2)垂直于半径的直线是圆的切线.( )
(3)过直径的外端并且垂直于这条直径的直线是圆的切线.( )
(4)和圆有一个公共点的直线是圆的切线.( )
(5)以等腰三角形的顶点为圆心,底边上的高为半径的圆与底边相切.( )
2、以三角形的一边为直径的圆恰好与另一边相切,则此三角形是__________三角形
直角
3、已知,如图在 中,AB为直径,AD为弦,过B点的切线与AD的延长线交于点C且 AD=DC则 ABD= 。
45
O
D
C
B
A
4.如图,⊙O的半径为3cm,B为⊙O外一点,OB交⊙O于点A,AB=OA,动点P从点A出发,以πcm/s的速度在⊙O上按逆时针方向运动一周回到点A立即停止.当点P运动的时间为 s时,BP与⊙O相切.
1或5
P1
5.如图, AB是⊙O的直径,∠B=45°,
AC=AB, AC是⊙O的切线吗?
为什么?
C
B
A
0
6.如图,在△ABC中 ∠ABC=90°,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED
求证:DE是⊙O的切线
·
O
A
C
B
E
D
7.如图,已知,AB是⊙O直径,BC⊥AB于B,⊙O的弦AD∥OC,
求证:DC是⊙O的切线.
D
O
B
C
A
8,如图,△ABC为等腰三角形,O为底边BC的中点,OD⊥AB,以O为圆心OD为半径作⊙O,
求证:AC与⊙O相切.
9.已知:如图, 梯形ABCD中,AD‖BC,∠C=90°,AD+BC=AB,以AB为直径作⊙O.
求证:CD为⊙O的切线.
.
A
D
O
B
C
.
1、如何判定一条直线是已知圆的切线?
(1)和圆只有一个公共点的直线是圆的切线;
(2)和圆心的距离等于半径的直线是圆的切线;
(3)过半径外端且和半径垂直的直线是圆的切线;
(d=r)
1、经过圆上的一点;
2、 垂直于半径;
2、圆的切线有什么性质?
圆的切线垂直于经过切点的半径。
小结
同课章节目录
