北师大版九年级数学上册 6.3 反比例函数的应用 同步练习题(Word版 含答案)
文档属性
| 名称 | 北师大版九年级数学上册 6.3 反比例函数的应用 同步练习题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 113.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 22:10:54 | ||
图片预览




文档简介
109474000001231900006.3 反比例函数的应用 同步练习题
(满分120分;时间:120分钟)-736600
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如表,根据表中数据,可得y关于x的函数表达式为(? ? ? ? )
近视眼镜的度数y(度)
200
250
400
500
1000
镜片焦距x(米)
0.50
0.40
0.25
0.20
0.10
A.y=100x B.y=x100 C.y=400x D.y=x400
?
2. 如图,直线y=x+a-2与双曲线y=4x交于A、B两点,则当线段AB的长度取最小值时,a的值为( )
A.0 B.1 C.2 D.5
?
3. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图,当气球内的气压大于120kPa时,气球将爆炸,为了安全起见,气体的体积应( )
A.小于54m3 B.大于45m3 C.不小于45m3 D.小于45m3
?
4. 某长方体的体积为100cm3,长方体的高h(单位:cm)与底面积S的函数关系式为( )
A.h=S100 B.h=100S C.h=100S D.h=100
?
5. 如图,一次函数y1=x-1与反比例函数y2=2x的图象交于点A、B,则使y1>y2的x的取值范围是( )
A.x>2 B.-12或-12或x<-1
?
6. 在一个体积可以改变的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度会随之改变,若密度ρ(单位:kg/m3)与体积V(单位:m3)满足的关系为ρ=8V,则当V=2时,气体的密度是( )
A.2kg/m3 B.4kg/m3 C.8kg/m3 D.16kg/m3
?
7. 如图,一次函数y1=ax+b图象和反比例函数y2=kx图象交于A(1,?2),B(-2,?-1)两点,若y1
A.x<-2 B.x<-2或01
?
8. 如图,已知第一象限内的点A在反比例函数y=2x的图象上,第二象限内的点B在反比例函数y=kx的图象上,且OA⊥OB,tanA=3,则k的值为( )
A.-3 B.-3 C.-6 D.-23
?
9. 如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y=10x B.y=5x C.y=20x D.y=x20
?
10. 如图,A、B是双曲线y=kx(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若△AOC的面积为8,则k的值为( )
A.43 B.83 C.163 D.4
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 设一个矩形长为x,宽为y,若其面积为2,则y与x函数关系的图象在________象限.
?
12. 有一块长方形试验田面积为3×106m2,试验田长y(单位:m)与宽x(单位:m)之间的函数关系式是________.
?
13. 近视眼镜的度数y(度)与焦距x(米)的函数关系式为y=100x,已知某同学近视眼镜镜片的焦距为0.25米,则该同学配的镜片的度数是________度.
?
14. 已知正比例函数y=ax(a≠0)与反比例函数y=kx(k≠0)图象的一个交点坐标为(-1,?-1),则另一个交点坐标是________.
?
15. 双十一时小明在网上买了一套课外读物,共360页,计划每天看一部分,则他阅读的天数y(天)和每天阅读的页数x(页)之间的函数解析式为________.
?
16. 如图,正比例函数y=12x的图象与反比例函数y=kx(k≠0)在第一象限的图象交于点A,过点A作x轴的垂线,垂足为点M,且△OAM的面积为1.若点B(1,?m)为反比例函数在第一象限图象上的一点,点P在x轴上,且使PA+PB最小,则点P的坐标为________.
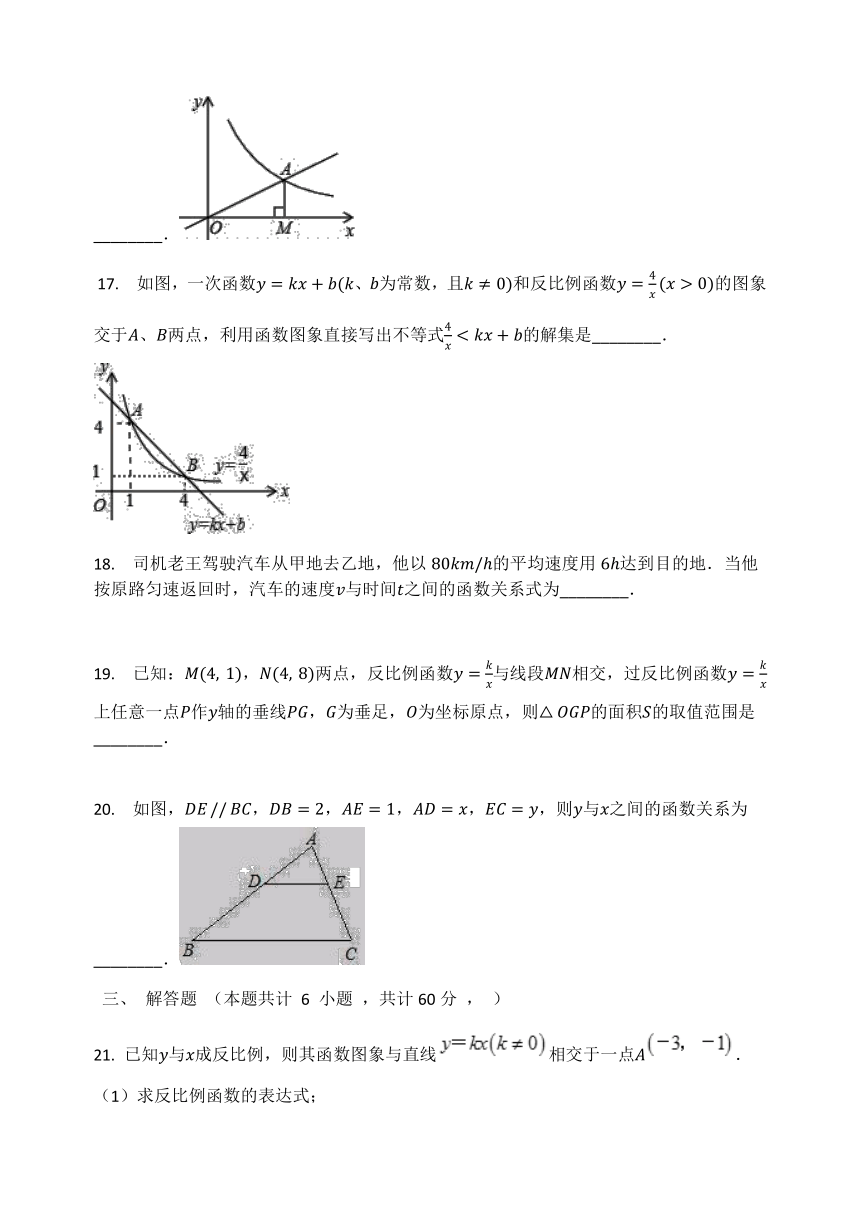
?17. 如图,一次函数y=kx+b(k、b为常数,且k≠0)和反比例函数y=4x(x>0)的图象交于A、B两点,利用函数图象直接写出不等式4x?
18. 司机老王驾驶汽车从甲地去乙地,他以80km/h的平均速度用6h达到目的地.当他按原路匀速返回时,汽车的速度v与时间t之间的函数关系式为________.
?
19. 已知:M(4,?1),N(4,?8)两点,反比例函数y=kx与线段MN相交,过反比例函数y=kx上任意一点P作y轴的垂线PG,G为垂足,O为坐标原点,则△OGP的面积S的取值范围是________.
?
20. 如图,DE?//?BC,DB=2,AE=1,AD=x,EC=y,则y与x之间的函数关系为________.
三、 解答题 (本题共计 6 小题 ,共计60分 , )
21. 已知y与x成反比例,则其函数图象与直线相交于一点A.
(1)求反比例函数的表达式;
(2)直接写出反比例函数图象与直线y=kx的另一个交点坐标;
(3)写出反比例函数值不小于正比例函数值时的x的取值范围.
?
22. 如图所示,已知正方形OABC的面积为9,点B在函数y=kx(k>0,x>0)的图象上,点P(m,?n)(6≤m≤9)是函数y=kx(k>0,x>0)的图象上动点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,若设矩形OEPF和正方形OABC不重合的两部分的面积和为S.
(1)求B点坐标和k的值;
(2)写出S关于m的函数关系和S的最大值.
?
23. 如图,直线y=kx+2k(k≠0)与x轴交于点B,与反比例函数y=(m+5)x2m+1的图象交于点A、C,其中点A在第一象限,点C在第三象限.
(1)求反比例函数的解析式;
(2)求B点的坐标;
(3)若△AOB的面积是2,求k的值.
?
24. 若矩形的长为x,宽为y,面积保持不变,下表给出了x与y的一些值求矩形面积.
(1)请你根据表格信息写出y与x之间的函数关系式;
(2)根据函数关系式完成上表.
?
25. 若一次函数的图象与x轴、y轴分别交于点A(-2,?0)、点B(0,?2).????
(1)求一次函数的解析式.
(2)若点C在x轴上,且OC=23,请直接写出∠ABC的度数.
(3)若直线EF经过点B且平行于X轴,交反比例函数y=-4x于点E,交反比例函数y=2x于点F,点P是x轴上一动点,请直接写出△PEF的面积.
?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
A
2.
【答案】
C
3.
【答案】
D
4.
【答案】
B
5.
【答案】
C
6.
【答案】
B
7.
【答案】
B
8.
【答案】
C
9.
【答案】
C
10.
【答案】
C
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
第一
12.
【答案】
y=3×106x
13.
【答案】
400
14.
【答案】
(1,?1)
15.
【答案】
y=360x
16.
【答案】
(53,?0)
17.
【答案】
118.
【答案】
v=480t
19.
【答案】
2≤S≤16
20.
【答案】
y=2x
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
(1)y=3x;见详解;
(2)另一个交点的坐标是3,1;见详解;
(3)022.
【答案】
解:(1)∵ 正方形OABC的面积为9,
∴ 正方形OABC的边长为3,即OA=3,AB=3,
∴ B点坐标为(3,?3);
又∵ 点B是函数kx的图象上的一点,
∴ 3=k3,
∴ k=9;
(2)由6≤m≤9,得到点P在点B的右侧,则PE=n,AE=m-3,
∴ S=PE?AE+CF?BC=n(m-3)+3(3-n)=9m(m-3)+9-3n=18-3n-27m,
当6≤m≤9时,反比例函数p=27m为减函数,S为关于m的增函数,
∴ 当m=9时,S取得最大值,此时最大值为18-3-279=15-3=12.
23.
【答案】
解:(1)依题意得:m+5≠0且2m+1=-1,解得m=-1
∴ m+5=4,
∴ 反比例函数的解析式为:y=4x;
(2)对于y=kx+2k(k≠0),令y=0,则kx+2k=0
∵ k≠0
∴ x=-2,即点B坐标为:(-2,?0);
(3)设A(a,?b),OB=2,
∵ S△AOB=2,
∴ 12×OB×b=2,
∴ b=2,
而点A在y=4x的图象上,
∴ ab=4,
∴ a=2,即点A的坐标为(2,?2),
把A(2,?2)代入y=kx+2k中,
∴ 2=2k+2k,
∴ k=12.
24.
【答案】
解:(1)设y=kx,
由于(1,?4)在此函数解析式上,那么k=1×4=4,
∴ y=4x;
(2)4÷23=4×32=6,
42=22,
4÷2=2,
48=12,
422=2.
25.
【答案】
解:(1)∵ 一次函数的图象与x轴、y轴分别交于点A(-2,?0)、点B(0,?2),
∴ 设一次函数解析式为y=kx+b,则b=2-2k+b=0,
解得:k=1b=2
∴ 一次函数的解析式为:y=x+2;
?????????????????????????
(2)当点C在正半轴时,∵ A(-2,?0)、点B(0,?2),
∴ AO=BO=2,
∴ ∠ABO=45?,
∵ BO=2,CO=23,
∴ tan∠CBO=232=3,
∴ ∠CBO=60?,
∴ ∠ABC=60?+45?=105?,
同理可得出:C在负半轴上时,∠ABC'=60?-45?=15?;
综上所述:在正半轴或负半轴,正半轴时∠ABC=105?,C在负半轴上时∠ABC=15?;
??????????
(3)∵ 直线EF经过点B且平行于X轴,交反比例函数y=-4x于点E,交反比例函数y=2x于点F,
∴ E点横坐标为:3=-4x,则x=-43,
F点横坐标为:3=2x,则x=23,
∴ EF=23-(43)=2,
s△PEF=12×2×3=3.
(满分120分;时间:120分钟)-736600
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如表,根据表中数据,可得y关于x的函数表达式为(? ? ? ? )
近视眼镜的度数y(度)
200
250
400
500
1000
镜片焦距x(米)
0.50
0.40
0.25
0.20
0.10
A.y=100x B.y=x100 C.y=400x D.y=x400
?
2. 如图,直线y=x+a-2与双曲线y=4x交于A、B两点,则当线段AB的长度取最小值时,a的值为( )
A.0 B.1 C.2 D.5
?
3. 某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图,当气球内的气压大于120kPa时,气球将爆炸,为了安全起见,气体的体积应( )
A.小于54m3 B.大于45m3 C.不小于45m3 D.小于45m3
?
4. 某长方体的体积为100cm3,长方体的高h(单位:cm)与底面积S的函数关系式为( )
A.h=S100 B.h=100S C.h=100S D.h=100
?
5. 如图,一次函数y1=x-1与反比例函数y2=2x的图象交于点A、B,则使y1>y2的x的取值范围是( )
A.x>2 B.-1
?
6. 在一个体积可以改变的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度会随之改变,若密度ρ(单位:kg/m3)与体积V(单位:m3)满足的关系为ρ=8V,则当V=2时,气体的密度是( )
A.2kg/m3 B.4kg/m3 C.8kg/m3 D.16kg/m3
?
7. 如图,一次函数y1=ax+b图象和反比例函数y2=kx图象交于A(1,?2),B(-2,?-1)两点,若y1
A.x<-2 B.x<-2或0
?
8. 如图,已知第一象限内的点A在反比例函数y=2x的图象上,第二象限内的点B在反比例函数y=kx的图象上,且OA⊥OB,tanA=3,则k的值为( )
A.-3 B.-3 C.-6 D.-23
?
9. 如果等腰三角形的面积为10,底边长为x,底边上的高为y,则y与x的函数关系式为( )
A.y=10x B.y=5x C.y=20x D.y=x20
?
10. 如图,A、B是双曲线y=kx(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若△AOC的面积为8,则k的值为( )
A.43 B.83 C.163 D.4
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
11. 设一个矩形长为x,宽为y,若其面积为2,则y与x函数关系的图象在________象限.
?
12. 有一块长方形试验田面积为3×106m2,试验田长y(单位:m)与宽x(单位:m)之间的函数关系式是________.
?
13. 近视眼镜的度数y(度)与焦距x(米)的函数关系式为y=100x,已知某同学近视眼镜镜片的焦距为0.25米,则该同学配的镜片的度数是________度.
?
14. 已知正比例函数y=ax(a≠0)与反比例函数y=kx(k≠0)图象的一个交点坐标为(-1,?-1),则另一个交点坐标是________.
?
15. 双十一时小明在网上买了一套课外读物,共360页,计划每天看一部分,则他阅读的天数y(天)和每天阅读的页数x(页)之间的函数解析式为________.
?
16. 如图,正比例函数y=12x的图象与反比例函数y=kx(k≠0)在第一象限的图象交于点A,过点A作x轴的垂线,垂足为点M,且△OAM的面积为1.若点B(1,?m)为反比例函数在第一象限图象上的一点,点P在x轴上,且使PA+PB最小,则点P的坐标为________.
?17. 如图,一次函数y=kx+b(k、b为常数,且k≠0)和反比例函数y=4x(x>0)的图象交于A、B两点,利用函数图象直接写出不等式4x
18. 司机老王驾驶汽车从甲地去乙地,他以80km/h的平均速度用6h达到目的地.当他按原路匀速返回时,汽车的速度v与时间t之间的函数关系式为________.
?
19. 已知:M(4,?1),N(4,?8)两点,反比例函数y=kx与线段MN相交,过反比例函数y=kx上任意一点P作y轴的垂线PG,G为垂足,O为坐标原点,则△OGP的面积S的取值范围是________.
?
20. 如图,DE?//?BC,DB=2,AE=1,AD=x,EC=y,则y与x之间的函数关系为________.
三、 解答题 (本题共计 6 小题 ,共计60分 , )
21. 已知y与x成反比例,则其函数图象与直线相交于一点A.
(1)求反比例函数的表达式;
(2)直接写出反比例函数图象与直线y=kx的另一个交点坐标;
(3)写出反比例函数值不小于正比例函数值时的x的取值范围.
?
22. 如图所示,已知正方形OABC的面积为9,点B在函数y=kx(k>0,x>0)的图象上,点P(m,?n)(6≤m≤9)是函数y=kx(k>0,x>0)的图象上动点,过点P分别作x轴、y轴的垂线,垂足分别为E、F,若设矩形OEPF和正方形OABC不重合的两部分的面积和为S.
(1)求B点坐标和k的值;
(2)写出S关于m的函数关系和S的最大值.
?
23. 如图,直线y=kx+2k(k≠0)与x轴交于点B,与反比例函数y=(m+5)x2m+1的图象交于点A、C,其中点A在第一象限,点C在第三象限.
(1)求反比例函数的解析式;
(2)求B点的坐标;
(3)若△AOB的面积是2,求k的值.
?
24. 若矩形的长为x,宽为y,面积保持不变,下表给出了x与y的一些值求矩形面积.
(1)请你根据表格信息写出y与x之间的函数关系式;
(2)根据函数关系式完成上表.
?
25. 若一次函数的图象与x轴、y轴分别交于点A(-2,?0)、点B(0,?2).????
(1)求一次函数的解析式.
(2)若点C在x轴上,且OC=23,请直接写出∠ABC的度数.
(3)若直线EF经过点B且平行于X轴,交反比例函数y=-4x于点E,交反比例函数y=2x于点F,点P是x轴上一动点,请直接写出△PEF的面积.
?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
A
2.
【答案】
C
3.
【答案】
D
4.
【答案】
B
5.
【答案】
C
6.
【答案】
B
7.
【答案】
B
8.
【答案】
C
9.
【答案】
C
10.
【答案】
C
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
第一
12.
【答案】
y=3×106x
13.
【答案】
400
14.
【答案】
(1,?1)
15.
【答案】
y=360x
16.
【答案】
(53,?0)
17.
【答案】
1
【答案】
v=480t
19.
【答案】
2≤S≤16
20.
【答案】
y=2x
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
(1)y=3x;见详解;
(2)另一个交点的坐标是3,1;见详解;
(3)0
【答案】
解:(1)∵ 正方形OABC的面积为9,
∴ 正方形OABC的边长为3,即OA=3,AB=3,
∴ B点坐标为(3,?3);
又∵ 点B是函数kx的图象上的一点,
∴ 3=k3,
∴ k=9;
(2)由6≤m≤9,得到点P在点B的右侧,则PE=n,AE=m-3,
∴ S=PE?AE+CF?BC=n(m-3)+3(3-n)=9m(m-3)+9-3n=18-3n-27m,
当6≤m≤9时,反比例函数p=27m为减函数,S为关于m的增函数,
∴ 当m=9时,S取得最大值,此时最大值为18-3-279=15-3=12.
23.
【答案】
解:(1)依题意得:m+5≠0且2m+1=-1,解得m=-1
∴ m+5=4,
∴ 反比例函数的解析式为:y=4x;
(2)对于y=kx+2k(k≠0),令y=0,则kx+2k=0
∵ k≠0
∴ x=-2,即点B坐标为:(-2,?0);
(3)设A(a,?b),OB=2,
∵ S△AOB=2,
∴ 12×OB×b=2,
∴ b=2,
而点A在y=4x的图象上,
∴ ab=4,
∴ a=2,即点A的坐标为(2,?2),
把A(2,?2)代入y=kx+2k中,
∴ 2=2k+2k,
∴ k=12.
24.
【答案】
解:(1)设y=kx,
由于(1,?4)在此函数解析式上,那么k=1×4=4,
∴ y=4x;
(2)4÷23=4×32=6,
42=22,
4÷2=2,
48=12,
422=2.
25.
【答案】
解:(1)∵ 一次函数的图象与x轴、y轴分别交于点A(-2,?0)、点B(0,?2),
∴ 设一次函数解析式为y=kx+b,则b=2-2k+b=0,
解得:k=1b=2
∴ 一次函数的解析式为:y=x+2;
?????????????????????????
(2)当点C在正半轴时,∵ A(-2,?0)、点B(0,?2),
∴ AO=BO=2,
∴ ∠ABO=45?,
∵ BO=2,CO=23,
∴ tan∠CBO=232=3,
∴ ∠CBO=60?,
∴ ∠ABC=60?+45?=105?,
同理可得出:C在负半轴上时,∠ABC'=60?-45?=15?;
综上所述:在正半轴或负半轴,正半轴时∠ABC=105?,C在负半轴上时∠ABC=15?;
??????????
(3)∵ 直线EF经过点B且平行于X轴,交反比例函数y=-4x于点E,交反比例函数y=2x于点F,
∴ E点横坐标为:3=-4x,则x=-43,
F点横坐标为:3=2x,则x=23,
∴ EF=23-(43)=2,
s△PEF=12×2×3=3.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
