人教版九年级数学上册 24.3 正多边形和圆 同步测试题(Word版 含答案)
文档属性
| 名称 | 人教版九年级数学上册 24.3 正多边形和圆 同步测试题(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 284.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 22:17:06 | ||
图片预览


文档简介
108077001264920012319000024.3 正多边形和圆 同步测试题
(满分120分;时间:120分钟)-736600
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
A.102 B.20 C.18 D.202
?
2. 正六边形的中心到边的距离为3,则该正六边形的面积是( )
A.63 B.123 C.6 D.12
?
3. 圆内接四边形ABCD的四个内角之比可能是( )
A.1:2:3:4 B.1:3:4:5 C.2:3:4:5 D.2:3:5:4
?
4. 中心角为60?的正多边形的边数是(? ? ? ? )
A.3 B.6 C.8 D.12
?
5. 内接于半径为1的圆的正方形的面积是( )
A.22 B.2 C.2 D.4
?
6. 圆内接四边形ABCD中,已知∠A=70?,则∠C等于( )
A.110? B.70? C.30? D.20?
?
7. 已知圆内接四边形ABCD,且AB的度数:BC的度数:CD的度数:DA的度数为1:2:3:4,则∠A:∠B:∠C:∠D等于( )
A.1:2:3:4 B.4:3:2:1 C.4:3:1:2 D.5:7:5:3
?
8. 在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为( )
A.7 B.6 C.5 D.4
?
9. 在⊙O中,弦AB=AC=BC=2cm,则此圆的半径为( )
A.33 B.233 C.12 D.2
?
10. 有一个长为12cm的正六边形,若要剪一张圆形纸片完全盖住这个圆形,则这个圆形纸片的半径最小是( )
A.10cm B.12cm C.14cm D.16cm
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 圆内接正六边形的半径为2cm,则其边长等于________.
?
12. 如图,AB是半圆的直径,点C、D是半圆上两点,∠ABC=50?,则∠ADC=________.
?
13. 如图,已知四边形ABCD内接于⊙O,∠ABC=60?,则∠CDE的度数是________. ?
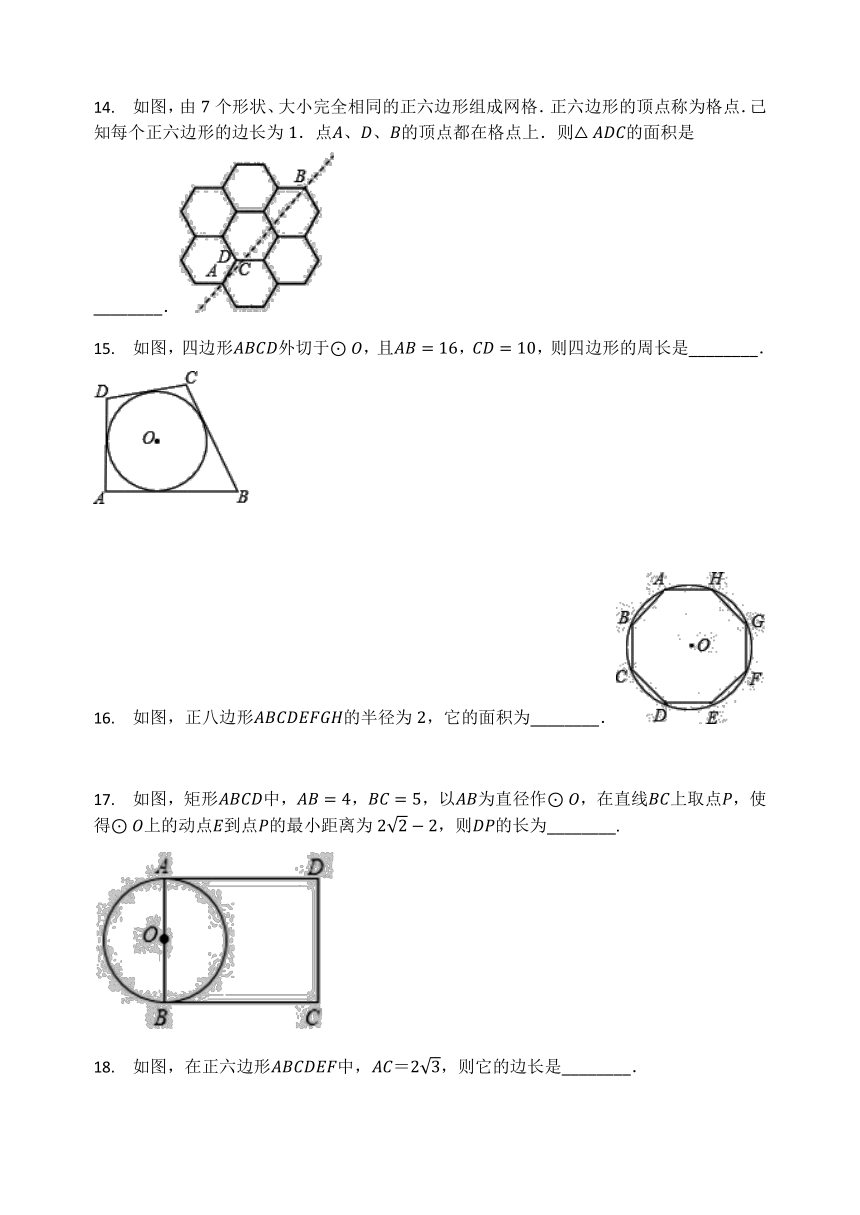
14. 如图,由7个形状、大小完全相同的正六边形组成网格.正六边形的顶点称为格点.己知每个正六边形的边长为1.点A、D、B的顶点都在格点上.则△ADC的面积是________. ?
15. 如图,四边形ABCD外切于⊙O,且AB=16,CD=10,则四边形的周长是________.
?
16. 如图,正八边形ABCDEFGH的半径为2,它的面积为________.
?
17. 如图,矩形ABCD中,AB=4,BC=5,以AB为直径作⊙O,在直线BC上取点P,使得⊙O上的动点E到点P的最小距离为22-2,则DP的长为________.
?
18. 如图,在正六边形ABCDEF中,AC=23,则它的边长是________.
?
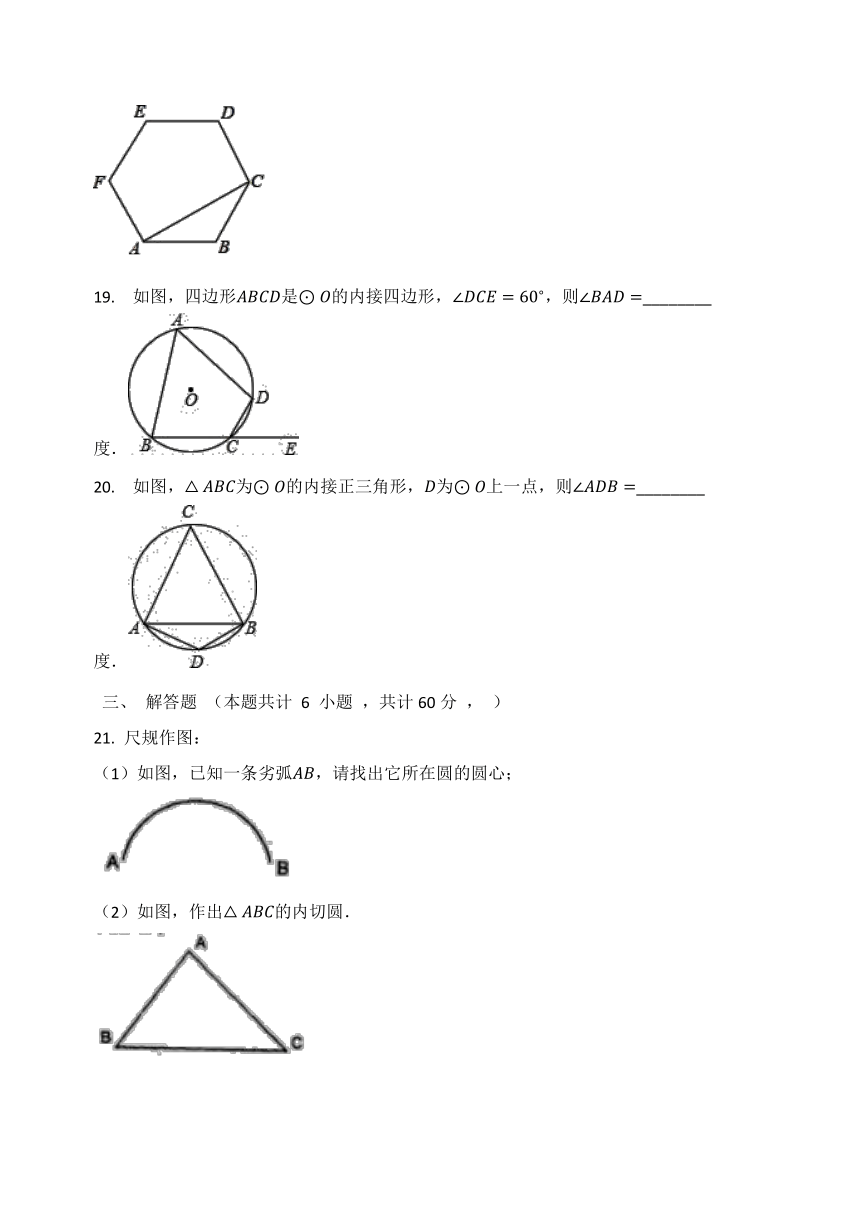
19. 如图,四边形ABCD是⊙O的内接四边形,∠DCE=60?,则∠BAD=________度. ?
20. 如图,△ABC为⊙O的内接正三角形,D为⊙O上一点,则∠ADB=________度.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 尺规作图:
(1)如图,已知一条劣弧AB,请找出它所在圆的圆心;
(2)如图,作出△ABC的内切圆.
?
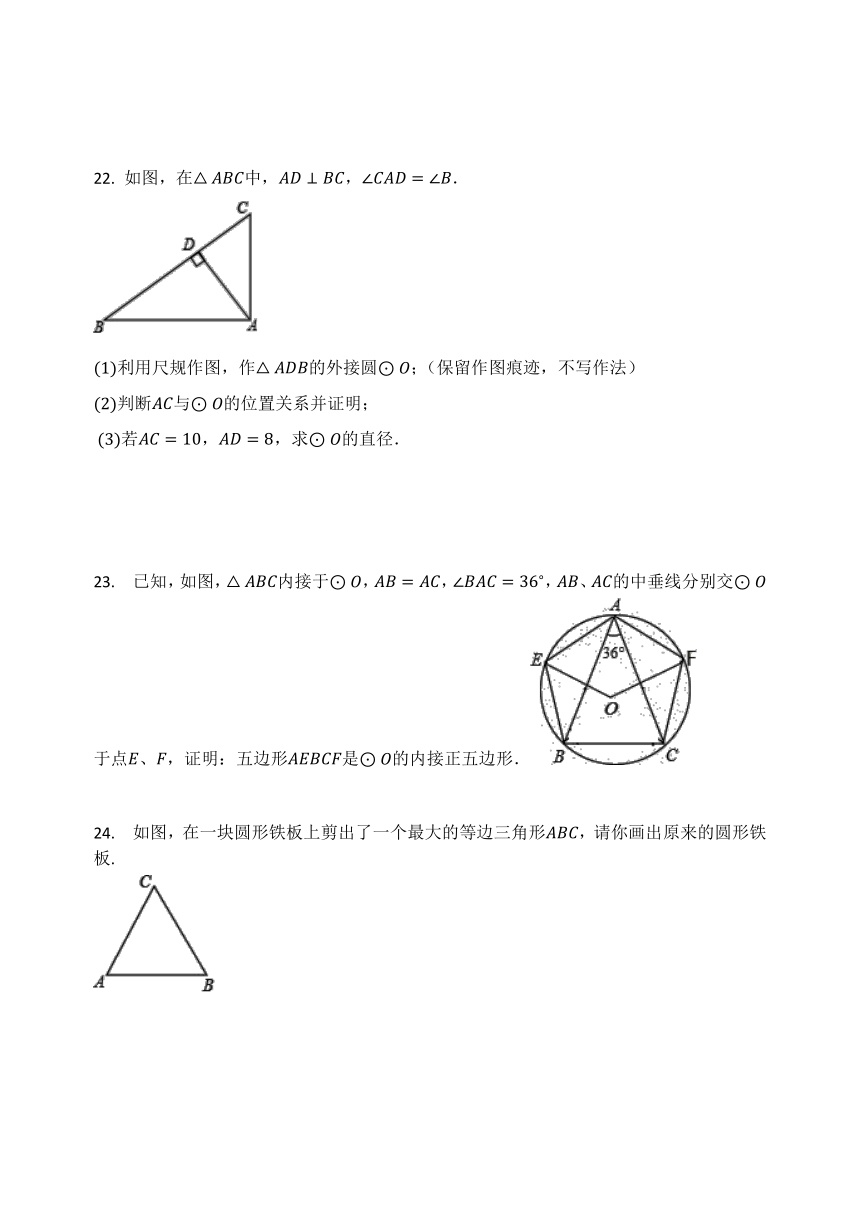
22. 如图,在△ABC中,AD⊥BC,∠CAD=∠B.
(1)利用尺规作图,作△ADB的外接圆⊙O;(保留作图痕迹,不写作法)
(2)判断AC与⊙O的位置关系并证明;
(3)若AC=10,AD=8,求⊙O的直径.
?
23. 已知,如图,△ABC内接于⊙O,AB=AC,∠BAC=36?,AB、AC的中垂线分别交⊙O于点E、F,证明:五边形AEBCF是⊙O的内接正五边形.
?
24. 如图,在一块圆形铁板上剪出了一个最大的等边三角形ABC,请你画出原来的圆形铁板.
?
25. 如图,⊙O1和⊙O2都经过A,B两点,经过点A的直线CD交⊙O1于C,交⊙O2于D,经过点B的直线EF交⊙O1于E,交⊙O2于F.求证:CE?//?DF.
?
26. (1)已知:如图1,四边形ABCD内接于⊙O,延长BC至E.求证:∠A+∠BCD=180?,∠DCE=∠A.
(2)依已知条件和(1)中的结论:
①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180?的大小关系;
②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180?的大小关系.
参考答案与试题解析
2020年11月7日初中数学
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
2.
【答案】
A
3.
【答案】
D
4.
【答案】
B
5.
【答案】
C
6.
【答案】
A
7.
【答案】
D
8.
【答案】
C
9.
【答案】
B
10.
【答案】
B
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
2cm
12.
【答案】
130?
13.
【答案】
60?
14.
【答案】
316
15.
【答案】
52
16.
【答案】
82
17.
【答案】
5或65
18.
【答案】
2
19.
【答案】
60
20.
【答案】
120
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
22.
【答案】
解:(1)根据题意,可作如图所示,
(2)AC是⊙O的切线,
证明如下:
∵ AD⊥BC,
∴ ∠ADB=90?,
∴ ∠B+∠BAD=90?,
又∵ ∠CAD=∠B,
∴ ∠CAD+∠BAD=90?,
即∠BAC=90?,
∴ AC是⊙O的切线.
(3)∵ ∠CAD=∠B,∠ADC=∠BDA=90?,
∴ △ACD?△BAD,
在Rt△ACD中,CD=6,
∴ AD:AB=CD:AC,
∴ AB=403.
23.
【答案】
证明:连接BF,CE,
∵ AB=AC,
∴ ∠ABC=∠ACB,
又∵ ∠BAC=36?,
∴ ∠ABC=∠ACB=72?.
又∵ AB、AC的中垂线分别交⊙O于点E、F,
∴ AF=CF,AE=BE,
∴ ∠BAC=∠BCE=∠ACE=∠ABF=∠FBC=36?,
∴ AE=AF=BE=BC=FC,
∴ AE=AF=BE=BC=FC,
∴ ∠EAF=∠AFC=∠FCB=∠CBE=∠BEA.
∴ 五边形AEBCD为正五边形.
24.
【答案】
解:如图,⊙O即为所求.
25.
【答案】
证明:连接AB.
∵ 四边形ABEC是⊙O1的内接四边形,
∴ ∠BAD=∠E.
又∵ 四边形ABFD是⊙O2的内接四边形,
∴ ∠BAD+∠F=180?.
∴ ∠E+∠F=180?.
∴ CE?//?DF.
26.
【答案】
解:(1)连接AC,BD,
则:∠1=∠4,∠2=∠7,∠3=∠6,∠5=∠8,
∴ ∠BAD+∠ABC+∠BCD+∠CDA=∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8=2(∠1+∠2+∠5+∠6)=360?,
∴ ∠1+∠2+∠5+∠6=180?,
∴ ∠A+∠BCD=180?;
∵ ∠DCE+∠BCD=180?,
∴ ∠DCE=∠A;
(2)①连接DE,
∵ ∠A+∠BED=180?,∠BDE>∠BCD,
∴ ∠A+∠BCD<180?;
②延长DC交⊙O于点E,连接BE,
∵ ∠A+∠E=180?,∠BCD>∠E,
∴ ∠A+∠BCD>180?.
(满分120分;时间:120分钟)-736600
真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!
题号
一
二
三
总分
得分
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , ) ?
1. 如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
A.102 B.20 C.18 D.202
?
2. 正六边形的中心到边的距离为3,则该正六边形的面积是( )
A.63 B.123 C.6 D.12
?
3. 圆内接四边形ABCD的四个内角之比可能是( )
A.1:2:3:4 B.1:3:4:5 C.2:3:4:5 D.2:3:5:4
?
4. 中心角为60?的正多边形的边数是(? ? ? ? )
A.3 B.6 C.8 D.12
?
5. 内接于半径为1的圆的正方形的面积是( )
A.22 B.2 C.2 D.4
?
6. 圆内接四边形ABCD中,已知∠A=70?,则∠C等于( )
A.110? B.70? C.30? D.20?
?
7. 已知圆内接四边形ABCD,且AB的度数:BC的度数:CD的度数:DA的度数为1:2:3:4,则∠A:∠B:∠C:∠D等于( )
A.1:2:3:4 B.4:3:2:1 C.4:3:1:2 D.5:7:5:3
?
8. 在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为( )
A.7 B.6 C.5 D.4
?
9. 在⊙O中,弦AB=AC=BC=2cm,则此圆的半径为( )
A.33 B.233 C.12 D.2
?
10. 有一个长为12cm的正六边形,若要剪一张圆形纸片完全盖住这个圆形,则这个圆形纸片的半径最小是( )
A.10cm B.12cm C.14cm D.16cm
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
11. 圆内接正六边形的半径为2cm,则其边长等于________.
?
12. 如图,AB是半圆的直径,点C、D是半圆上两点,∠ABC=50?,则∠ADC=________.
?
13. 如图,已知四边形ABCD内接于⊙O,∠ABC=60?,则∠CDE的度数是________. ?
14. 如图,由7个形状、大小完全相同的正六边形组成网格.正六边形的顶点称为格点.己知每个正六边形的边长为1.点A、D、B的顶点都在格点上.则△ADC的面积是________. ?
15. 如图,四边形ABCD外切于⊙O,且AB=16,CD=10,则四边形的周长是________.
?
16. 如图,正八边形ABCDEFGH的半径为2,它的面积为________.
?
17. 如图,矩形ABCD中,AB=4,BC=5,以AB为直径作⊙O,在直线BC上取点P,使得⊙O上的动点E到点P的最小距离为22-2,则DP的长为________.
?
18. 如图,在正六边形ABCDEF中,AC=23,则它的边长是________.
?
19. 如图,四边形ABCD是⊙O的内接四边形,∠DCE=60?,则∠BAD=________度. ?
20. 如图,△ABC为⊙O的内接正三角形,D为⊙O上一点,则∠ADB=________度.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 尺规作图:
(1)如图,已知一条劣弧AB,请找出它所在圆的圆心;
(2)如图,作出△ABC的内切圆.
?
22. 如图,在△ABC中,AD⊥BC,∠CAD=∠B.
(1)利用尺规作图,作△ADB的外接圆⊙O;(保留作图痕迹,不写作法)
(2)判断AC与⊙O的位置关系并证明;
(3)若AC=10,AD=8,求⊙O的直径.
?
23. 已知,如图,△ABC内接于⊙O,AB=AC,∠BAC=36?,AB、AC的中垂线分别交⊙O于点E、F,证明:五边形AEBCF是⊙O的内接正五边形.
?
24. 如图,在一块圆形铁板上剪出了一个最大的等边三角形ABC,请你画出原来的圆形铁板.
?
25. 如图,⊙O1和⊙O2都经过A,B两点,经过点A的直线CD交⊙O1于C,交⊙O2于D,经过点B的直线EF交⊙O1于E,交⊙O2于F.求证:CE?//?DF.
?
26. (1)已知:如图1,四边形ABCD内接于⊙O,延长BC至E.求证:∠A+∠BCD=180?,∠DCE=∠A.
(2)依已知条件和(1)中的结论:
①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180?的大小关系;
②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180?的大小关系.
参考答案与试题解析
2020年11月7日初中数学
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
B
2.
【答案】
A
3.
【答案】
D
4.
【答案】
B
5.
【答案】
C
6.
【答案】
A
7.
【答案】
D
8.
【答案】
C
9.
【答案】
B
10.
【答案】
B
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
2cm
12.
【答案】
130?
13.
【答案】
60?
14.
【答案】
316
15.
【答案】
52
16.
【答案】
82
17.
【答案】
5或65
18.
【答案】
2
19.
【答案】
60
20.
【答案】
120
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
22.
【答案】
解:(1)根据题意,可作如图所示,
(2)AC是⊙O的切线,
证明如下:
∵ AD⊥BC,
∴ ∠ADB=90?,
∴ ∠B+∠BAD=90?,
又∵ ∠CAD=∠B,
∴ ∠CAD+∠BAD=90?,
即∠BAC=90?,
∴ AC是⊙O的切线.
(3)∵ ∠CAD=∠B,∠ADC=∠BDA=90?,
∴ △ACD?△BAD,
在Rt△ACD中,CD=6,
∴ AD:AB=CD:AC,
∴ AB=403.
23.
【答案】
证明:连接BF,CE,
∵ AB=AC,
∴ ∠ABC=∠ACB,
又∵ ∠BAC=36?,
∴ ∠ABC=∠ACB=72?.
又∵ AB、AC的中垂线分别交⊙O于点E、F,
∴ AF=CF,AE=BE,
∴ ∠BAC=∠BCE=∠ACE=∠ABF=∠FBC=36?,
∴ AE=AF=BE=BC=FC,
∴ AE=AF=BE=BC=FC,
∴ ∠EAF=∠AFC=∠FCB=∠CBE=∠BEA.
∴ 五边形AEBCD为正五边形.
24.
【答案】
解:如图,⊙O即为所求.
25.
【答案】
证明:连接AB.
∵ 四边形ABEC是⊙O1的内接四边形,
∴ ∠BAD=∠E.
又∵ 四边形ABFD是⊙O2的内接四边形,
∴ ∠BAD+∠F=180?.
∴ ∠E+∠F=180?.
∴ CE?//?DF.
26.
【答案】
解:(1)连接AC,BD,
则:∠1=∠4,∠2=∠7,∠3=∠6,∠5=∠8,
∴ ∠BAD+∠ABC+∠BCD+∠CDA=∠1+∠2+∠3+∠4+∠5+∠6+∠7+∠8=2(∠1+∠2+∠5+∠6)=360?,
∴ ∠1+∠2+∠5+∠6=180?,
∴ ∠A+∠BCD=180?;
∵ ∠DCE+∠BCD=180?,
∴ ∠DCE=∠A;
(2)①连接DE,
∵ ∠A+∠BED=180?,∠BDE>∠BCD,
∴ ∠A+∠BCD<180?;
②延长DC交⊙O于点E,连接BE,
∵ ∠A+∠E=180?,∠BCD>∠E,
∴ ∠A+∠BCD>180?.
同课章节目录
