人教版数学八年级上册 13.2画对称图形同步测试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学八年级上册 13.2画对称图形同步测试题(一)(Word版 含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 263.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 00:00:00 | ||
图片预览

文档简介
画对称图形同步测试题(一)
一.选择题
1.已知点M(2,2),规定一次变换是:先作点M关于x轴对称,再将对称点向左平移1个单位长度,则连续经过2020次变换后,点M的坐标变为( )
A. C.
2.若点A(﹣4,m﹣3),B(2n,1)关于x轴对称,则( )
A.m=2,n=0 B.m=2,n=﹣2 C.m=4,n=2 D.m=4,n=﹣2
3.如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到△A'B'C',那么点B的对应点B'的坐标为( )
A. C.
4.如图,已知正方形ABCD的对角线AC,BD相交于点M,顶点A、B、C的坐标分别为(1,3)、(1,1)、(3,1),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2020次变换后,点M的坐标变为( )
A. C.
5.若直线a经过(0,9),直线b经过(4,3),且a与b关于x轴对称,则a与b的交点的坐标为( )
A. C.
6.已知,点A(m﹣1,3)与点B(2,n﹣1)关于x轴对称,则(m+n)2020的值为( )
A.0 B.1 C.﹣1 D.32020
7.平面直角坐标系中,点P(3,1)关于x轴对称的点的坐标是( )
A. C.
8.关于x的不等式组恰有5个整数解,且点A(a,3)不在坐标轴上,则A点关于x轴的对称点在第( )象限.
A.一、二 B.二、三 C.三、四 D.一、四
9.如图,等边△ABC的顶点A(1,1),B(3,1),规定把△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,这样连续经过2020次变换后,等边△ABC的顶点C的坐标为( )
A.(﹣2 020,) B.(﹣2 019,)
C.(﹣2 018,) D.(﹣2 017,)
10.如图,已知△ABC的三个顶点A(a,0)、B(b,0)、C(0,2a)(b>a>0),作△ABC关于直线AC的对称图形△AB1C,若点B1恰好落在y轴上,则的值为( )
A. B. C. D.
二.填空题
11.点P(﹣4,9)关于x轴对称点P′的坐标是 .
12.若点(3+m,a﹣2)关于y轴对称点的坐标是(3,2),则m+a的值为 .
13.如图,已知A(2,2)、B(﹣4,1),点P在y轴上.
(1)写出A点关于y轴对称点A'的坐标 .
(2)当y轴平分∠APB时,点P的坐标为 .
14.如图,点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,则a+b= .
三.解答题
15.如图,在长方形网格中有一个△ABC.
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)若网格中的最小正方形边长为1,求△A1B1C1的面积.
16.已知:如图,在Rt△ABC中,∠C=90°,∠A≠∠B.
(1)请利用直尺和圆规作出△ABC关于直线AC对称的△AGC;(不要求写作法,保留作图痕迹)
(2)在AG边上找一点D,使得BD的中点E满足CE=AD.请利用直尺和圆规作出点D和点E.(不要求写作法,保留作图痕迹)
17.如图,在10×8的正方形网格中,每个小正方形的边长都为1.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线MN对称的△A1B1C1(要求A与A1、B与B1、C与C1相对应);
(2)求△ABC的面积.
18.;
(2)直接写出△A1B1C1三点的坐标:A1 ,B1 ,C1 .
(3)直接写出△ABC的面积是 .
19.如图,在正方形网格中,每个小正方形的边长均为1个单位,每个小正方形的顶点叫做格点,△ABC的三个顶点都在格点上.
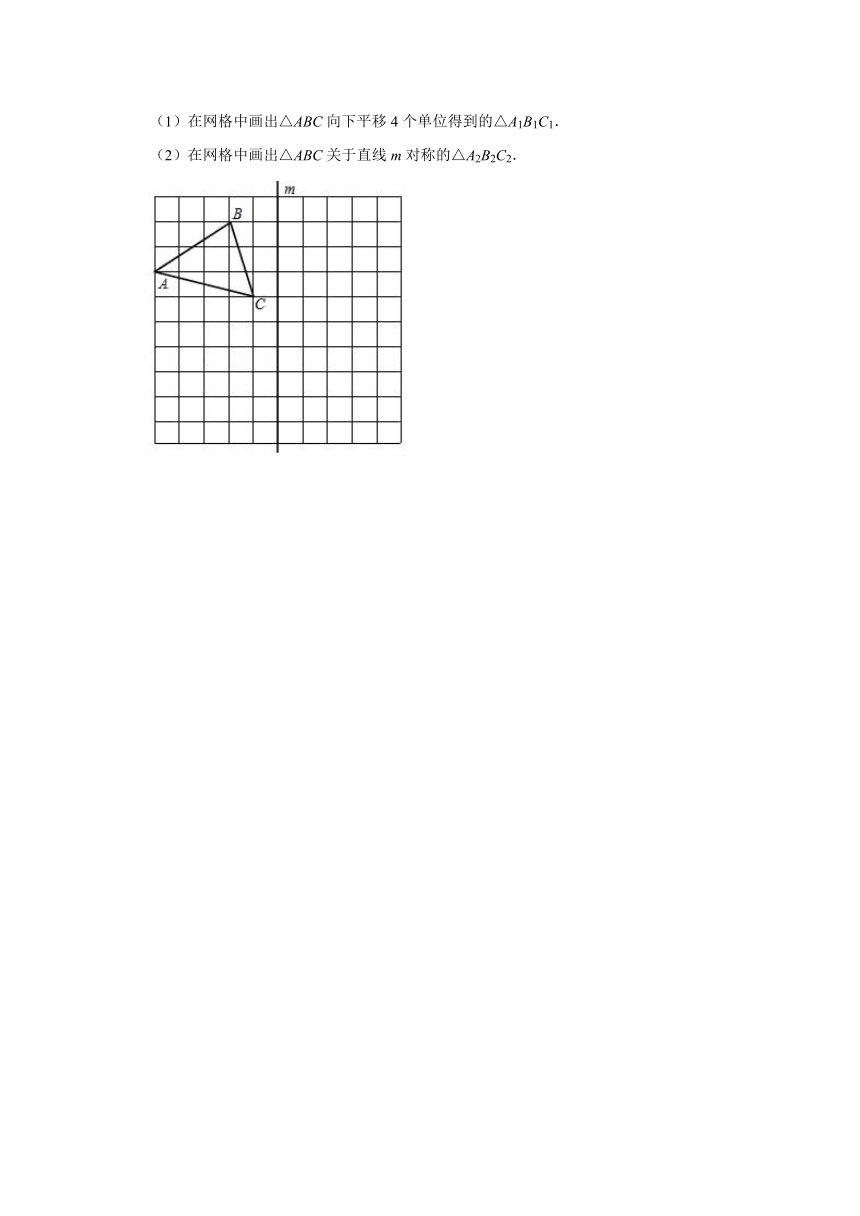
(1)在网格中画出△ABC向下平移4个单位得到的△A1B1C1.
(2)在网格中画出△ABC关于直线m对称的△A2B2C2.
参考答案与试题解析
一.
1.【解答】解:由题可得,第2019次变换后的点M在x轴下方,
∴点M的纵坐标为2,横坐标为2﹣2020×1=﹣2018,
∴点M的坐标变为(﹣2018,﹣2),
故选:B.
2.【解答】解:根据题意:
m﹣3=﹣1,2n=﹣4,
所以m=2,n=﹣2.
故选:B.
3.【解答】解:由坐标系可得B(﹣3,1),将△ABC先沿y轴翻折得到B点对应点为(3,1),再向上平移3个单位长度,点B的对应点B'的坐标为(3,1+3),
即(3,4),
故选:C.
4.【解答】解:∵正方形ABCD,顶点A(1,3),B(1,1),C(3,1),
∴对角线交点M的坐标为(2,2),
根据题意得:第1次变换后的点M的对应点的坐标为(2+1,﹣2),即(3,﹣2),
第2次变换后的点M的对应点的坐标为:(2+2,2),即(4,2),
第3次变换后的点M的对应点的坐标为(2+3,﹣2),即(5,﹣2),
第n次变换后的点M的对应点的坐标为:当n为奇数时为(2+n,﹣2),当n为偶数时为(2+n,2),
∴连续经过2020次变换后,正方形ABCD的对角线交点M的坐标变为(2022,2).
故选:A.
5.【解答】解:∵直线a经过(0,9),直线b经过(4,3),且a与b关于x轴对称,
∴直线a经过(4,﹣3),直线b经过(0,﹣9),
设直线a的解析式为:y=kx+c,
则,
解得:k=﹣3,
故直线a的解析式为:y=﹣3x+9;
设直线b的解析式为:y=dx+e,
则,
解得:d=3,
故直线a的解析式为:y=3x﹣9;
则,
解得:,
即a与b的交点的坐标为(3,0).
故选:A.
6.【解答】解:∵点A(m﹣1,3)与点B(2,n﹣1)关于x轴对称,
∴m﹣1=2,n﹣1=﹣3,
∴m=3,n=﹣2,
∵(m+n)2020=1,
故选:B.
7.【解答】解:点P(3,1)关于x轴对称的点的坐标是(3,﹣1)
故选:B.
8.【解答】解:不等式组的解集为,
∵不等式组有5个整数解,
∴整数解为﹣1、0、1、2、3,
∴,
解得﹣1≤a<2,
又∵点A(a,3)不在坐标轴上,
∴﹣1≤a<0或0<a<2,
∴A点在第一象限或第二象限,
∴A点关于x轴的对称点在第四象限或第三象限.
故选:C.
9.【解答】解:∵△ABC是等边三角形AB=3﹣1=2,
∴点C到x轴的距离为1+2×=+1,
横坐标为2,
∴C(2, +1),
第2020次变换后的三角形在x轴上方,
点C的纵坐标为+1,横坐标为2﹣2020×1=﹣2018,
∴点C的对应点C′的坐标是(﹣2018, +1),
故选:C.
10.【解答】解:如图,连接BB′,延长CA交BB′于M.
∵B,B′关于AC对称,
∴CM⊥BB′,
∵∠ACO+∠CAO=90°,∠ABM+∠MAB=90°,∠CAO=∠MAB,
∴∠ACO=∠ABM,
∵∠AOC=∠BOB′=90°,
∴△AOC∽△B′OB,
∴=,
∴=,
∴OB′=,
在Rt△AOB′中,∵AB′2=AO2+OB′2,
∴(b﹣a)2=a2+()2,
∴3b2﹣8ab=0,
∵b≠0,
∴b=a,
∴=.
故选:D.
二.填空题
11.【解答】解:点P(﹣4,9)关于x轴对称点P′的坐标是:(﹣4,﹣9).
故答案为:(﹣4,﹣9).
12.【解答】解:∵点(3+m,a﹣2)关于y轴对称点的坐标是(3,2),
∴3+m=﹣3,a﹣2=2,
解得:m=﹣6,a=4,
则m+a的值为:﹣6+4=﹣2.
故答案为:﹣2.
13.【解答】解:(1)∵A(2,2),
∴A点关于y轴对称点A'的坐标(﹣2,2);
(2)如图,当y轴平分∠APB时,点A关于y的对称点A'在BP上,
∵A(2,2),
∴A'(﹣2,2),
设A'B的表达式为y=kx+b,
把A'(﹣2,2),B(﹣4,1)代入,
可得,
解得,
∴y=,
令x=0,则y=3,
∴点P的坐标为(0,3),
故答案为:(1)A'(﹣2,2);(2)P(0,3).
14.【解答】解:∵点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,
∴a=﹣2,b=﹣3,
∴a+b=﹣2﹣3=﹣5,
故答案为﹣5.
三.解答题
15.【解答】解:(1)△A1B1C1即为所求;
(2)△A1B1C1的面积为:3×5﹣×2×3﹣×2×3﹣×1×5=15﹣3﹣3﹣2.5=6.5.
16.【解答】解:(1)所画△AGC见图.
(2)所画图形见图.
作图简要步骤如下:
①作AC的垂直平分线,交AC于F点;
②连接BF并延长,交AG于D点;
③作BD的垂直平分线,交BD于E点,连接CE.
则D点和E点为所求.
17.【解答】解:(1)如图所示,△A1B1C1即为所求;
(2)△ABC的面积为:3×4﹣﹣﹣=12﹣3﹣2﹣2=5.
18.【解答】解:(1)如图所示;
(2)A1(2,2),B1(3,0),C1(﹣1,﹣3),
故答案为:(2,2),(3,0),(﹣1,﹣3);
(3)△ABC的面积:4×5﹣×2×1﹣3×5﹣×4×3=5.5.
故答案为:5.5.
19.【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作
一.选择题
1.已知点M(2,2),规定一次变换是:先作点M关于x轴对称,再将对称点向左平移1个单位长度,则连续经过2020次变换后,点M的坐标变为( )
A. C.
2.若点A(﹣4,m﹣3),B(2n,1)关于x轴对称,则( )
A.m=2,n=0 B.m=2,n=﹣2 C.m=4,n=2 D.m=4,n=﹣2
3.如图,在平面直角坐标系中,△ABC的顶点都在格点上,如果将△ABC先沿y轴翻折,再向上平移3个单位长度,得到△A'B'C',那么点B的对应点B'的坐标为( )
A. C.
4.如图,已知正方形ABCD的对角线AC,BD相交于点M,顶点A、B、C的坐标分别为(1,3)、(1,1)、(3,1),规定“把正方形ABCD先沿x轴翻折,再向右平移1个单位”为一次变换,如此这样,连续经过2020次变换后,点M的坐标变为( )
A. C.
5.若直线a经过(0,9),直线b经过(4,3),且a与b关于x轴对称,则a与b的交点的坐标为( )
A. C.
6.已知,点A(m﹣1,3)与点B(2,n﹣1)关于x轴对称,则(m+n)2020的值为( )
A.0 B.1 C.﹣1 D.32020
7.平面直角坐标系中,点P(3,1)关于x轴对称的点的坐标是( )
A. C.
8.关于x的不等式组恰有5个整数解,且点A(a,3)不在坐标轴上,则A点关于x轴的对称点在第( )象限.
A.一、二 B.二、三 C.三、四 D.一、四
9.如图,等边△ABC的顶点A(1,1),B(3,1),规定把△ABC“先沿x轴翻折,再向左平移1个单位”为一次变换,这样连续经过2020次变换后,等边△ABC的顶点C的坐标为( )
A.(﹣2 020,) B.(﹣2 019,)
C.(﹣2 018,) D.(﹣2 017,)
10.如图,已知△ABC的三个顶点A(a,0)、B(b,0)、C(0,2a)(b>a>0),作△ABC关于直线AC的对称图形△AB1C,若点B1恰好落在y轴上,则的值为( )
A. B. C. D.
二.填空题
11.点P(﹣4,9)关于x轴对称点P′的坐标是 .
12.若点(3+m,a﹣2)关于y轴对称点的坐标是(3,2),则m+a的值为 .
13.如图,已知A(2,2)、B(﹣4,1),点P在y轴上.
(1)写出A点关于y轴对称点A'的坐标 .
(2)当y轴平分∠APB时,点P的坐标为 .
14.如图,点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,则a+b= .
三.解答题
15.如图,在长方形网格中有一个△ABC.
(1)画出△ABC关于y轴对称的△A1B1C1.
(2)若网格中的最小正方形边长为1,求△A1B1C1的面积.
16.已知:如图,在Rt△ABC中,∠C=90°,∠A≠∠B.
(1)请利用直尺和圆规作出△ABC关于直线AC对称的△AGC;(不要求写作法,保留作图痕迹)
(2)在AG边上找一点D,使得BD的中点E满足CE=AD.请利用直尺和圆规作出点D和点E.(不要求写作法,保留作图痕迹)
17.如图,在10×8的正方形网格中,每个小正方形的边长都为1.网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线MN对称的△A1B1C1(要求A与A1、B与B1、C与C1相对应);
(2)求△ABC的面积.
18.;
(2)直接写出△A1B1C1三点的坐标:A1 ,B1 ,C1 .
(3)直接写出△ABC的面积是 .
19.如图,在正方形网格中,每个小正方形的边长均为1个单位,每个小正方形的顶点叫做格点,△ABC的三个顶点都在格点上.
(1)在网格中画出△ABC向下平移4个单位得到的△A1B1C1.
(2)在网格中画出△ABC关于直线m对称的△A2B2C2.
参考答案与试题解析
一.
1.【解答】解:由题可得,第2019次变换后的点M在x轴下方,
∴点M的纵坐标为2,横坐标为2﹣2020×1=﹣2018,
∴点M的坐标变为(﹣2018,﹣2),
故选:B.
2.【解答】解:根据题意:
m﹣3=﹣1,2n=﹣4,
所以m=2,n=﹣2.
故选:B.
3.【解答】解:由坐标系可得B(﹣3,1),将△ABC先沿y轴翻折得到B点对应点为(3,1),再向上平移3个单位长度,点B的对应点B'的坐标为(3,1+3),
即(3,4),
故选:C.
4.【解答】解:∵正方形ABCD,顶点A(1,3),B(1,1),C(3,1),
∴对角线交点M的坐标为(2,2),
根据题意得:第1次变换后的点M的对应点的坐标为(2+1,﹣2),即(3,﹣2),
第2次变换后的点M的对应点的坐标为:(2+2,2),即(4,2),
第3次变换后的点M的对应点的坐标为(2+3,﹣2),即(5,﹣2),
第n次变换后的点M的对应点的坐标为:当n为奇数时为(2+n,﹣2),当n为偶数时为(2+n,2),
∴连续经过2020次变换后,正方形ABCD的对角线交点M的坐标变为(2022,2).
故选:A.
5.【解答】解:∵直线a经过(0,9),直线b经过(4,3),且a与b关于x轴对称,
∴直线a经过(4,﹣3),直线b经过(0,﹣9),
设直线a的解析式为:y=kx+c,
则,
解得:k=﹣3,
故直线a的解析式为:y=﹣3x+9;
设直线b的解析式为:y=dx+e,
则,
解得:d=3,
故直线a的解析式为:y=3x﹣9;
则,
解得:,
即a与b的交点的坐标为(3,0).
故选:A.
6.【解答】解:∵点A(m﹣1,3)与点B(2,n﹣1)关于x轴对称,
∴m﹣1=2,n﹣1=﹣3,
∴m=3,n=﹣2,
∵(m+n)2020=1,
故选:B.
7.【解答】解:点P(3,1)关于x轴对称的点的坐标是(3,﹣1)
故选:B.
8.【解答】解:不等式组的解集为,
∵不等式组有5个整数解,
∴整数解为﹣1、0、1、2、3,
∴,
解得﹣1≤a<2,
又∵点A(a,3)不在坐标轴上,
∴﹣1≤a<0或0<a<2,
∴A点在第一象限或第二象限,
∴A点关于x轴的对称点在第四象限或第三象限.
故选:C.
9.【解答】解:∵△ABC是等边三角形AB=3﹣1=2,
∴点C到x轴的距离为1+2×=+1,
横坐标为2,
∴C(2, +1),
第2020次变换后的三角形在x轴上方,
点C的纵坐标为+1,横坐标为2﹣2020×1=﹣2018,
∴点C的对应点C′的坐标是(﹣2018, +1),
故选:C.
10.【解答】解:如图,连接BB′,延长CA交BB′于M.
∵B,B′关于AC对称,
∴CM⊥BB′,
∵∠ACO+∠CAO=90°,∠ABM+∠MAB=90°,∠CAO=∠MAB,
∴∠ACO=∠ABM,
∵∠AOC=∠BOB′=90°,
∴△AOC∽△B′OB,
∴=,
∴=,
∴OB′=,
在Rt△AOB′中,∵AB′2=AO2+OB′2,
∴(b﹣a)2=a2+()2,
∴3b2﹣8ab=0,
∵b≠0,
∴b=a,
∴=.
故选:D.
二.填空题
11.【解答】解:点P(﹣4,9)关于x轴对称点P′的坐标是:(﹣4,﹣9).
故答案为:(﹣4,﹣9).
12.【解答】解:∵点(3+m,a﹣2)关于y轴对称点的坐标是(3,2),
∴3+m=﹣3,a﹣2=2,
解得:m=﹣6,a=4,
则m+a的值为:﹣6+4=﹣2.
故答案为:﹣2.
13.【解答】解:(1)∵A(2,2),
∴A点关于y轴对称点A'的坐标(﹣2,2);
(2)如图,当y轴平分∠APB时,点A关于y的对称点A'在BP上,
∵A(2,2),
∴A'(﹣2,2),
设A'B的表达式为y=kx+b,
把A'(﹣2,2),B(﹣4,1)代入,
可得,
解得,
∴y=,
令x=0,则y=3,
∴点P的坐标为(0,3),
故答案为:(1)A'(﹣2,2);(2)P(0,3).
14.【解答】解:∵点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,
∴a=﹣2,b=﹣3,
∴a+b=﹣2﹣3=﹣5,
故答案为﹣5.
三.解答题
15.【解答】解:(1)△A1B1C1即为所求;
(2)△A1B1C1的面积为:3×5﹣×2×3﹣×2×3﹣×1×5=15﹣3﹣3﹣2.5=6.5.
16.【解答】解:(1)所画△AGC见图.
(2)所画图形见图.
作图简要步骤如下:
①作AC的垂直平分线,交AC于F点;
②连接BF并延长,交AG于D点;
③作BD的垂直平分线,交BD于E点,连接CE.
则D点和E点为所求.
17.【解答】解:(1)如图所示,△A1B1C1即为所求;
(2)△ABC的面积为:3×4﹣﹣﹣=12﹣3﹣2﹣2=5.
18.【解答】解:(1)如图所示;
(2)A1(2,2),B1(3,0),C1(﹣1,﹣3),
故答案为:(2,2),(3,0),(﹣1,﹣3);
(3)△ABC的面积:4×5﹣×2×1﹣3×5﹣×4×3=5.5.
故答案为:5.5.
19.【解答】解:(1)如图,△A1B1C1为所作;
(2)如图,△A2B2C2为所作
