人教新课标版九年级数学上册 24.2.2直线和圆的位置关系(第3课时)课件
文档属性
| 名称 | 人教新课标版九年级数学上册 24.2.2直线和圆的位置关系(第3课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-19 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
自学指导: 课本96—98页内容
1.什么是点到圆的切线长?
2.解释96页探究上的问题,得到切线长定理是什么?
3.如何在三角形上截出一块面积最大的圆形?
4.什么是三角形的内切圆?什么是三角形的内心?
P
·
O
A
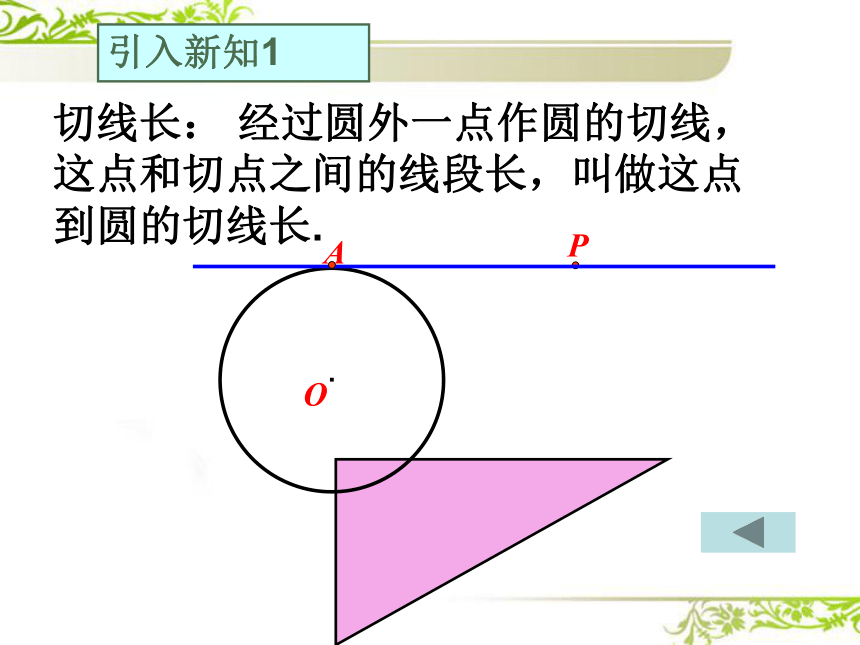
切线长: 经过圆外一点作圆的切线,这点和切点之间的线段长,叫做这点到圆的切线长.
引入新知1
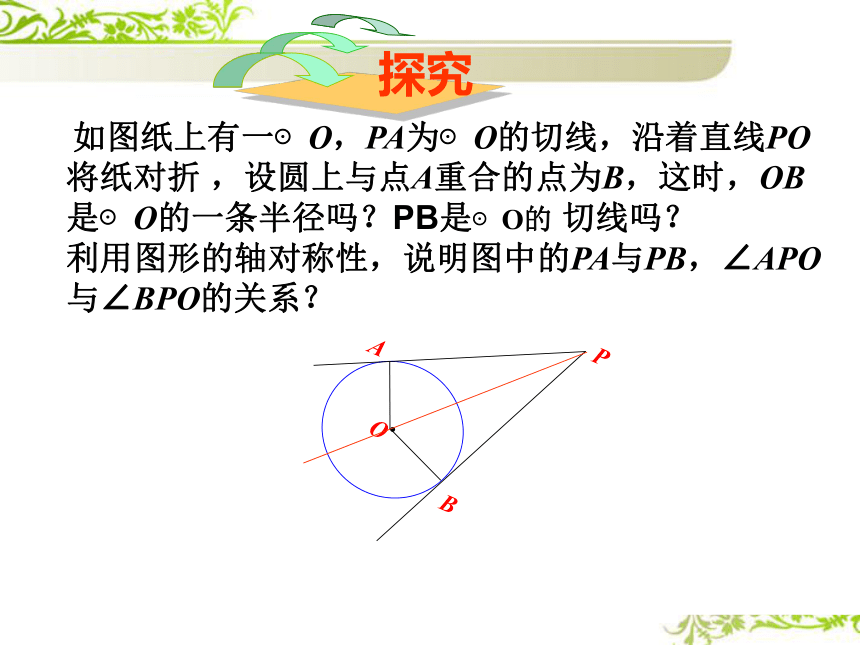
如图纸上有一⊙O,PA为⊙O的切线,沿着直线PO将纸对折 ,设圆上与点A重合的点为B,这时,OB是⊙O的一条半径吗?PB是⊙O的 切线吗?
探究
利用图形的轴对称性,说明图中的PA与PB,∠APO与∠BPO的关系?
P
B
·
O
A
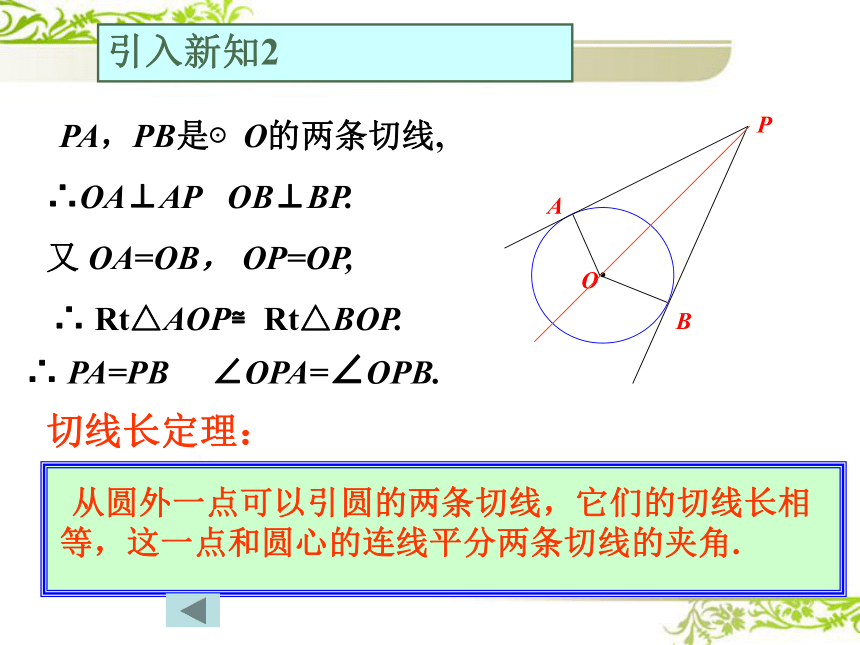
PA,PB是⊙O的两条切线,
∴OA⊥AP OB⊥BP.
又 OA=OB, OP=OP,
∴ Rt△AOP≌Rt△BOP.
∴ PA=PB ∠OPA=∠OPB.
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
切线长定理:
P
B
·
O
A
引入新知2
O
B
P
A
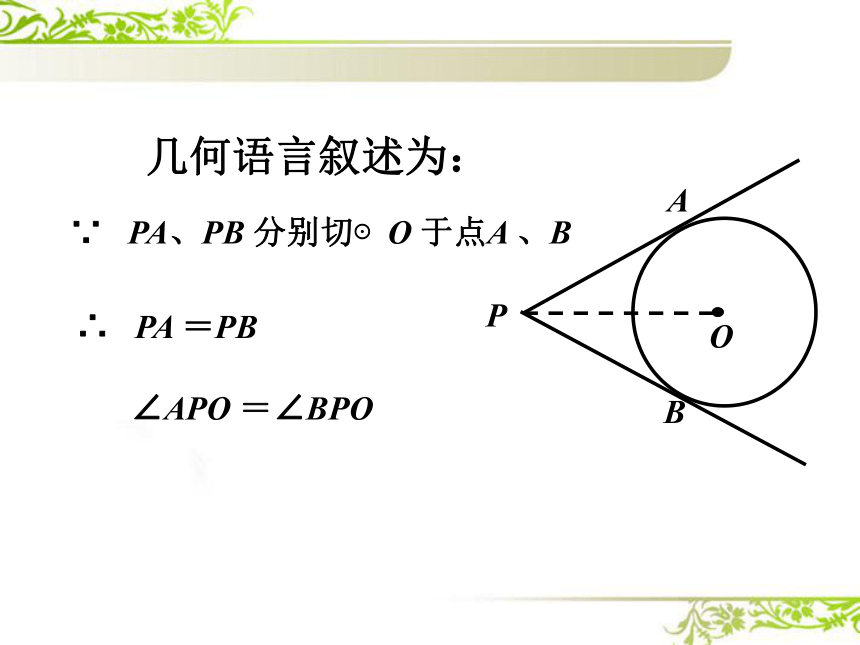
∵ PA、PB 分别切⊙O 于点A 、B
∴ PA =PB
∠APO =∠BPO
几何语言叙述为:
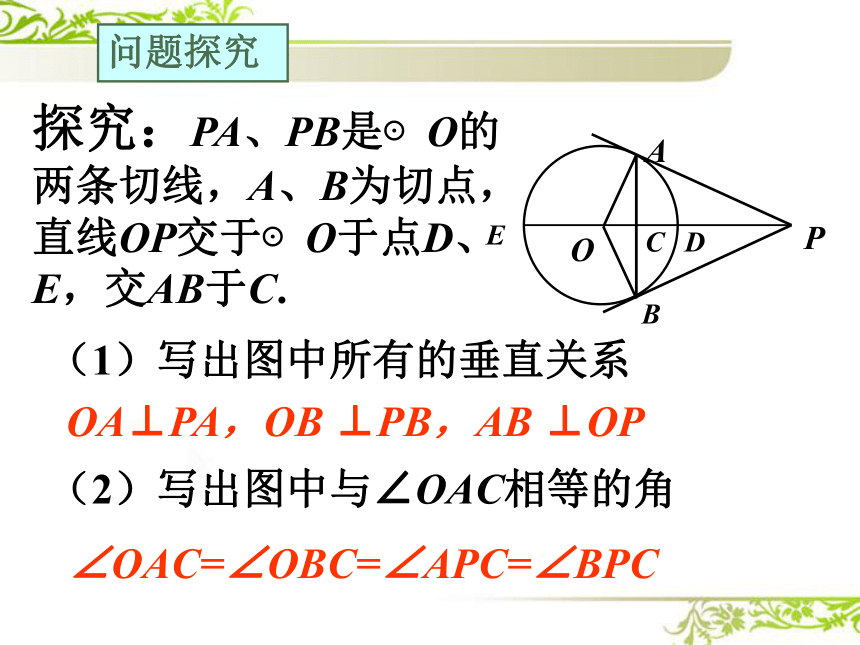
探究:PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C.
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
问题探究
(3)写出图中所有的全等三角形
△AOP≌ △BOP,
△AOC≌ △BOC,
△ACP≌ △BCP
(4)写出图中所有的等腰三角形
△ABP △AOB
课外练习
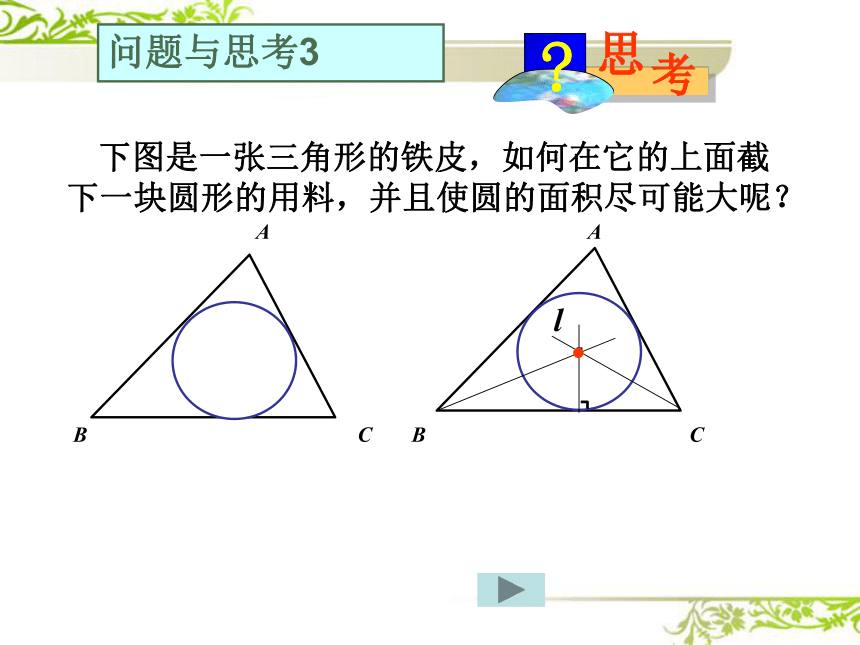
下图是一张三角形的铁皮,如何在它的上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
·
C
A
B
l
C
A
B
问题与思考3
假设符合条件的圆已经作出,那么它应当与三角形的三边都相切,这个圆的圆心到三角形的距离都等于半径,如何找到圆心?
C
A
B
议一议
三角形的三条角平分线交于一点,并且这个点到三条边的距离相等,因此,如图,分别作出∠B、∠C的平分线BM和CN,设他们相交于点I,那么点I到AB、BC、CA的距离都相等,以点I为圆心,点I到BC的距离ID为半径做圆,则⊙I与△ABC的三条边都相切.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
C
A
B
I
D
M
N
r
与三角形各边都相切的圆叫做三角形的内切圆,
引入新知4
例1 如图 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长.
解: 设 AF=x(cm),则
AE=x,
CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x,
由BD+CD=BC可得
(13-x)+(9-x)=14.
解得 x=4cm.
因此 AF=4(cm),
BD=5 (cm),
CE=9 (cm).
·
C
A
B
E
F
O
D
例题讲解
·
A
B
C
E
D
F
O
如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r.
设AD= x , BE= y ,CE= r
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
则有
x+r=b
y+r=a
x+y=c
解:设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
解得
r=
a+b-c
2
设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的
内切圆的半径 r= 或r=
a+b-c
2
ab
a+b+c
2.△ABC的内切圆半径为r, △ABC的周长为l,求△ABC的面积.(提示:设内心为O,连接OA、OB、OC.)
解: 设: AB = c BC = a AC = b
则
C
A
B
·
O
D
M
N
r
r
r
课堂练习
△
△
△
△
△
△
△
例2 、如图,四边形ABCD的边AB、BC、CD、DA和圆⊙O分别相切于点L、M、N、P,
求证: AD+BC=AB+CD
D
L
M
N
A
B
C
O
P
证明:由切线长定理得
∴AL=AP,LB=MB,NC=MC,
DN=DP
∴AL+LB+NC+DN=AP+MB+MC+DP
即 AB+CD=AD+BC
例题讲解
1.如图, △ABC中,∠ABC=50°∠ACB=75°,点O是内心,求∠BOC的读数.
解 :∠BOC=180°- (∠ABC + ∠ACB)
=117.5°
=180°- (50°+75°)
A
·
C
B
O
课堂练习
(2)已知OA=3cm,OP=6cm,则∠APB=
P
A
B
C
O
60°
(4)OP交⊙O于M,则 ,AB OP
AM=BM
⌒
⌒
M
⊥
(3)若∠APB=70°,则∠AOB= °
110
(1)若PA=4、PM=2,求圆O的半径OA
OA=3
巩固练习1
已知:PA、PB是⊙O的两条切线,
已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12cm,求(1)△PEF的周长.(2)如果∠P=46°,求∠AOB的度数
E
A
Q
P
F
B
O
易证EQ=EA, FQ=FB,
PA=PB
∴ PE+EQ=PA=12cm
PF+FQ=PB=PA=12cm
∴周长为24cm
巩固练习2
⌒
基础题:
1.既有外接圆,又内切圆的平行四边形是______.
2.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3.⊙O是边长为2cm的正方形ABCD的内切圆,EF切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.
E
F
H
G
正方形
22cm
2cm
切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
A
P
O
。
B
E
C
D
∵PA、PB分别切⊙O于A、B
∴PA = PB ,∠OPA=∠OPB
OP垂直平分AB
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用.
课堂小结
我们学过的切线,常有 五个 性质:
1、切线和圆只有一个公共点;
2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;
4、经过圆心垂直于切线的直线必过切点;
5、经过切点垂直于切线的直线必过圆心;
6、从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
六个
课堂小结
自学指导: 课本96—98页内容
1.什么是点到圆的切线长?
2.解释96页探究上的问题,得到切线长定理是什么?
3.如何在三角形上截出一块面积最大的圆形?
4.什么是三角形的内切圆?什么是三角形的内心?
P
·
O
A
切线长: 经过圆外一点作圆的切线,这点和切点之间的线段长,叫做这点到圆的切线长.
引入新知1
如图纸上有一⊙O,PA为⊙O的切线,沿着直线PO将纸对折 ,设圆上与点A重合的点为B,这时,OB是⊙O的一条半径吗?PB是⊙O的 切线吗?
探究
利用图形的轴对称性,说明图中的PA与PB,∠APO与∠BPO的关系?
P
B
·
O
A
PA,PB是⊙O的两条切线,
∴OA⊥AP OB⊥BP.
又 OA=OB, OP=OP,
∴ Rt△AOP≌Rt△BOP.
∴ PA=PB ∠OPA=∠OPB.
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
切线长定理:
P
B
·
O
A
引入新知2
O
B
P
A
∵ PA、PB 分别切⊙O 于点A 、B
∴ PA =PB
∠APO =∠BPO
几何语言叙述为:
探究:PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C.
B
A
P
O
C
E
D
(1)写出图中所有的垂直关系
OA⊥PA,OB ⊥PB,AB ⊥OP
(2)写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
问题探究
(3)写出图中所有的全等三角形
△AOP≌ △BOP,
△AOC≌ △BOC,
△ACP≌ △BCP
(4)写出图中所有的等腰三角形
△ABP △AOB
课外练习
下图是一张三角形的铁皮,如何在它的上面截下一块圆形的用料,并且使圆的面积尽可能大呢?
·
C
A
B
l
C
A
B
问题与思考3
假设符合条件的圆已经作出,那么它应当与三角形的三边都相切,这个圆的圆心到三角形的距离都等于半径,如何找到圆心?
C
A
B
议一议
三角形的三条角平分线交于一点,并且这个点到三条边的距离相等,因此,如图,分别作出∠B、∠C的平分线BM和CN,设他们相交于点I,那么点I到AB、BC、CA的距离都相等,以点I为圆心,点I到BC的距离ID为半径做圆,则⊙I与△ABC的三条边都相切.
内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
C
A
B
I
D
M
N
r
与三角形各边都相切的圆叫做三角形的内切圆,
引入新知4
例1 如图 △ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且AB=9cm,BC=14cm,CA=13cm,求AF、BD、CE的长.
解: 设 AF=x(cm),则
AE=x,
CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x,
由BD+CD=BC可得
(13-x)+(9-x)=14.
解得 x=4cm.
因此 AF=4(cm),
BD=5 (cm),
CE=9 (cm).
·
C
A
B
E
F
O
D
例题讲解
·
A
B
C
E
D
F
O
如图,Rt△ABC中,∠C=90°,BC=a,AC=b, AB=c,⊙O为Rt△ABC的内切圆. 求:Rt△ABC的内切圆的半径 r.
设AD= x , BE= y ,CE= r
∵ ⊙O与Rt△ABC的三边都相切
∴AD=AF,BE=BF,CE=CD
则有
x+r=b
y+r=a
x+y=c
解:设Rt△ABC的内切圆与三边相切于D、E、F,连结OD、OE、OF则OA⊥AC,OE⊥BC,OF⊥AB。
解得
r=
a+b-c
2
设Rt△ABC的直角边为a、b,斜边为c,则Rt△ABC的
内切圆的半径 r= 或r=
a+b-c
2
ab
a+b+c
2.△ABC的内切圆半径为r, △ABC的周长为l,求△ABC的面积.(提示:设内心为O,连接OA、OB、OC.)
解: 设: AB = c BC = a AC = b
则
C
A
B
·
O
D
M
N
r
r
r
课堂练习
△
△
△
△
△
△
△
例2 、如图,四边形ABCD的边AB、BC、CD、DA和圆⊙O分别相切于点L、M、N、P,
求证: AD+BC=AB+CD
D
L
M
N
A
B
C
O
P
证明:由切线长定理得
∴AL=AP,LB=MB,NC=MC,
DN=DP
∴AL+LB+NC+DN=AP+MB+MC+DP
即 AB+CD=AD+BC
例题讲解
1.如图, △ABC中,∠ABC=50°∠ACB=75°,点O是内心,求∠BOC的读数.
解 :∠BOC=180°- (∠ABC + ∠ACB)
=117.5°
=180°- (50°+75°)
A
·
C
B
O
课堂练习
(2)已知OA=3cm,OP=6cm,则∠APB=
P
A
B
C
O
60°
(4)OP交⊙O于M,则 ,AB OP
AM=BM
⌒
⌒
M
⊥
(3)若∠APB=70°,则∠AOB= °
110
(1)若PA=4、PM=2,求圆O的半径OA
OA=3
巩固练习1
已知:PA、PB是⊙O的两条切线,
已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12cm,求(1)△PEF的周长.(2)如果∠P=46°,求∠AOB的度数
E
A
Q
P
F
B
O
易证EQ=EA, FQ=FB,
PA=PB
∴ PE+EQ=PA=12cm
PF+FQ=PB=PA=12cm
∴周长为24cm
巩固练习2
⌒
基础题:
1.既有外接圆,又内切圆的平行四边形是______.
2.直角三角形的外接圆半径为5cm,内切圆半径为1cm,
则此三角形的周长是_______.
3.⊙O是边长为2cm的正方形ABCD的内切圆,EF切⊙O
于P点,交AB、BC于E、F,则△BEF的周长是_____.
E
F
H
G
正方形
22cm
2cm
切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
A
P
O
。
B
E
C
D
∵PA、PB分别切⊙O于A、B
∴PA = PB ,∠OPA=∠OPB
OP垂直平分AB
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用.
课堂小结
我们学过的切线,常有 五个 性质:
1、切线和圆只有一个公共点;
2、切线和圆心的距离等于圆的半径;
3、切线垂直于过切点的半径;
4、经过圆心垂直于切线的直线必过切点;
5、经过切点垂直于切线的直线必过圆心;
6、从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
六个
课堂小结
同课章节目录
