2020-2021学年青岛新版九年级上册数学《第1章 图形的相似》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年青岛新版九年级上册数学《第1章 图形的相似》单元测试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 316.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-07 22:34:49 | ||
图片预览



文档简介
2020-2021学年青岛新版九年级上册数学《第1章
图形的相似》单元测试卷
一.选择题(共10小题)
1.下列语句中的图形必成相似形的是( )
A.只有一个角为30°的等腰三角形
B.邻边之比为2的两个平行四边形
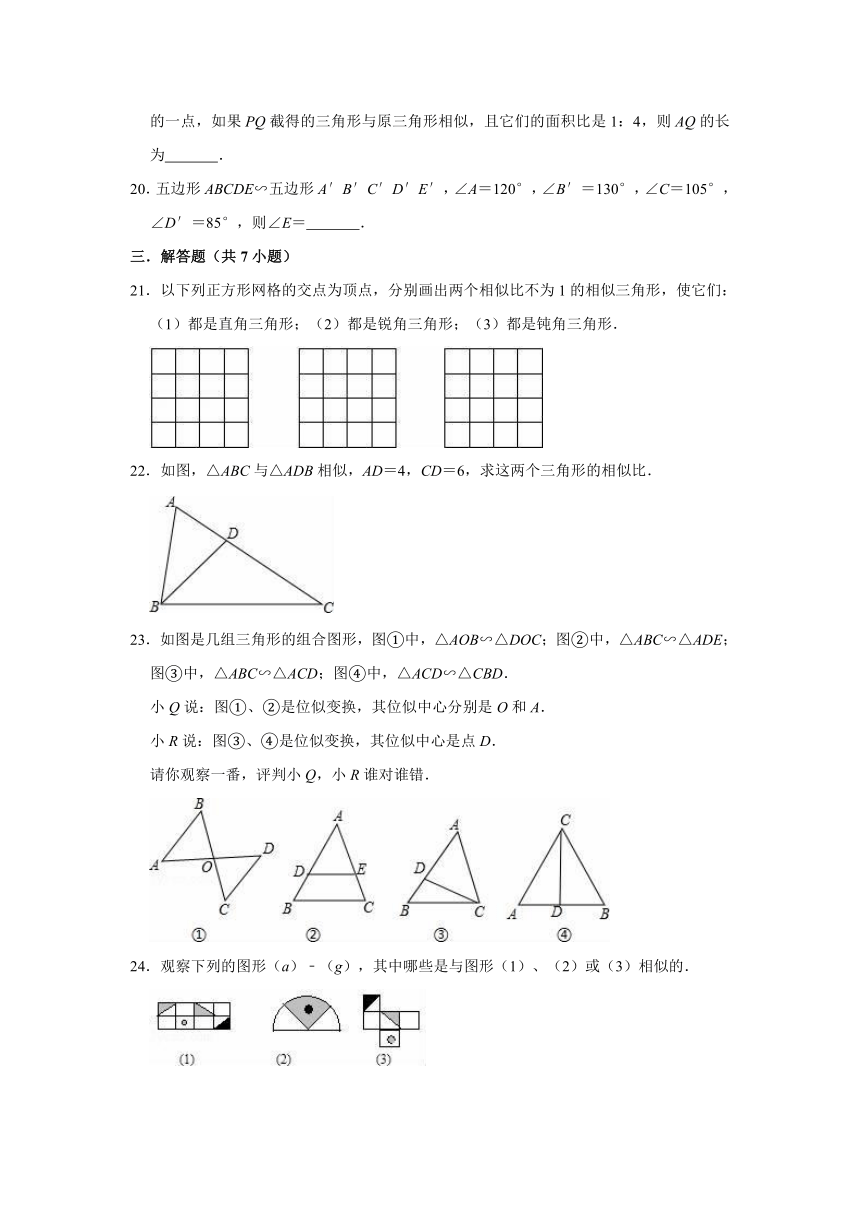
C.底角为40°的两个等腰梯形
D.有一个角为40°的两个等腰梯形
2.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B
B.∠ADE=∠C
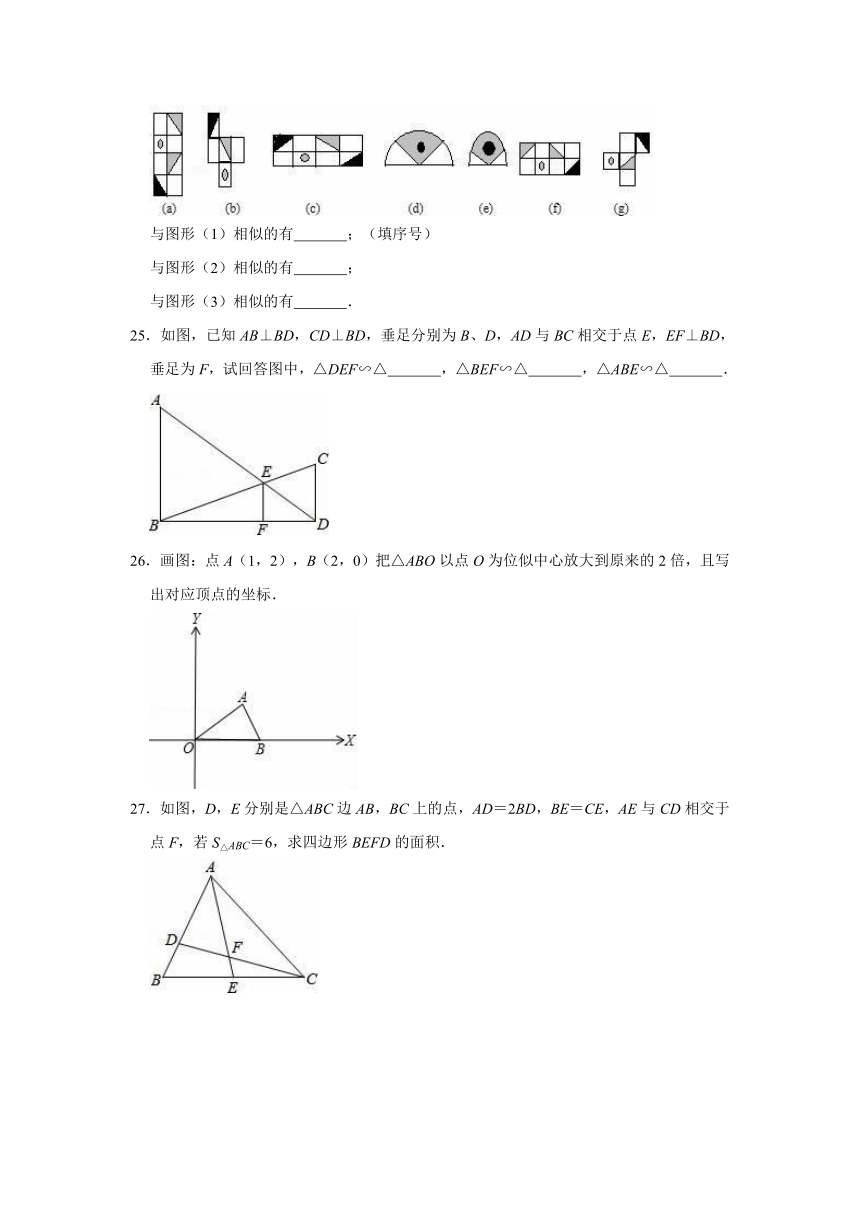
C.
D.
3.如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
A.
B.
C.
D.
4.在某一时刻测得1米高的竹竿的影长为0.9米,同时测得一棵树的影长,落在地面上的影长为1.8米,落在墙上的影长为0.4米,则这棵树的高度为( )
A.2米
B.2.4米
C.2.2米
D.2.8米
5.△ABC∽△A′B′C′,已知AB=5,A′B′=6,△ABC面积为10,那么另一个三角形的面积为( )
A.15
B.14.4
C.12
D.10.8
6.已知五边形ABCDE与五边形A1B1C1D1E1是两个位似的图形,它们面积的比为4:9,若位似中心O到A的距离为6,则O到A的对应点A1的距离为( )
A.4
B.
C.9
D.
7.如图,两个位似图形△ABO和△A′B′O,若OA:OA′=3:1,则正确的是( )
A.AB:A′B′=3:1
B.AA′:BB′=AB:AB′
C.OA:OB′=2:1
D.∠A=∠B′
8.如图所示,图中的三个矩形中相似的是( )
A.甲、乙和丙
B.甲和乙
C.甲和丙
D.乙和丙
9.张华同学的身高为160厘米,某一时刻他在阳光下的影子长为200厘米,与他相邻近的一棵树的影子长为6米,则这棵树的高为( )米.
A.3.2
B.4.8
C.5.2
D.5.6
10.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
二.填空题(共10小题)
11.如图,C、D是△PAB的边AB上的两点,以CD为边作平行四边形CDEF,EF经过点P,且
∠APB=∠ADE.试写出四对相似三角形
.
12.如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=
.
13.同一底片印出来的不同尺寸的照片也是
.
14.一个多边形的边长依次为1,2,3,4;5,6,7,8,与它位似的另一个多边形的最大边长为12,那么另一个多边形的周长为
.
15.如图,在△ABC中,∠A=36°,BD是角平分线,当∠C=
°时,△ABC∽△BDC.
16.已知△ABC∽△DEF,AB=21cm,DE=28cm,则△ABC和△DEF的相似比为
.
17.两个相似多边形的周长之比为2:3,而面积之差为12,则两个相似多边形的面积分别是
.
18.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度DM=150cm,CD=800cm,则树高AB=
cm.
19.△ABC中,AB=12,AC=8,P是BC上的一点,且BP=2PC,设Q是△ABC某边上的一点,如果PQ截得的三角形与原三角形相似,且它们的面积比是1:4,则AQ的长为
.
20.五边形ABCDE∽五边形A′B′C′D′E′,∠A=120°,∠B′=130°,∠C=105°,∠D′=85°,则∠E=
.
三.解答题(共7小题)
21.以下列正方形网格的交点为顶点,分别画出两个相似比不为1的相似三角形,使它们:
(1)都是直角三角形;(2)都是锐角三角形;(3)都是钝角三角形.
22.如图,△ABC与△ADB相似,AD=4,CD=6,求这两个三角形的相似比.
23.如图是几组三角形的组合图形,图①中,△AOB∽△DOC;图②中,△ABC∽△ADE;图③中,△ABC∽△ACD;图④中,△ACD∽△CBD.
小Q说:图①、②是位似变换,其位似中心分别是O和A.
小R说:图③、④是位似变换,其位似中心是点D.
请你观察一番,评判小Q,小R谁对谁错.
24.观察下列的图形(a)﹣(g),其中哪些是与图形(1)、(2)或(3)相似的.
与图形(1)相似的有
;(填序号)
与图形(2)相似的有
;
与图形(3)相似的有
.
25.如图,已知AB⊥BD,CD⊥BD,垂足分别为B、D,AD与BC相交于点E,EF⊥BD,垂足为F,试回答图中,△DEF∽△
,△BEF∽△
,△ABE∽△
.
26.画图:点A(1,2),B(2,0)把△ABO以点O为位似中心放大到原来的2倍,且写出对应顶点的坐标.
27.如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,AE与CD相交于点F,若S△ABC=6,求四边形BEFD的面积.
参考答案与试题解析
一.选择题(共10小题)
1.解:A、只有一个角为30°的等腰三角形,30°的角必定是顶角,所以,底角也一定相等,三角形相似,故本选项正确;
B、邻边之比为2,夹角不一定相等,两平行四边形不一定相似,故本选项错误;
C、底角为40°的等腰梯形,角对应相等,边不一定对应成比例,两等腰梯形不一定相似,故本选项错误;
D、有一个角为40°的等腰梯形,角对应相等,边不一定对应成比例,两等腰梯形不一定相似,故本选项错误.
故选:A.
2.解:A、∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故A选项错误;
B、∠ADE=∠C,∠A=∠A,则可判断△ADE∽△ACB,故B选项错误;
C、=不能判定△ADE∽△ACB,故B选项正确;
D、=,且夹角∠A=∠A,能确定△ADE∽△ACB,故D选项错误.
故选:C.
3.解:如图,过点E作HF⊥AB
∵AM∥CD,
∴∠DCE=∠EAM,∠CDE=∠EMA,
∴△AME∽△CDE
∴AM:DC=EH:EF=1:2,FH=AD=1
∴EH=,EF=.
∴阴影部分的面积=S正﹣S△AME﹣S△CDE﹣S△MBC=1﹣﹣﹣=.
故选:B.
4.解:设影长为1.8m时树的高度为hm,
∵在某一时刻测得直立的标杆长0.9m,其影长为1m,
∴,
解得x=2m,
∴树的高度=2+0.4=2.4m,
答:树的高度是2.4米.
故选:B.
5.解:∵△ABC∽△A′B′C′,AB=5,A′B′=6,
∴=,
∵△ABC面积为10,
∴解得:S△A′B′C′=14.4.
故选:B.
6.解:设点O到A1的距离为x,
∵它们面积的比为4:9,
∴(6:x)2=4:9,
解得x=9,
即:O到A的对应点A1的距离为9.
故选:C.
7.解:∵△ABO和△A′B′O是位似图形,
∴△ABO∽△A′B′O,
∴OA:OA′=AB:A′B′=3:1(A正确),
∠A=∠A′(D不正确),
B,C均无法证得.
故选:A.
8.解:∵都是矩形,
∴所有对应角相等;
∵甲与乙:≠,故不相似;
甲与丙:,故相似;
∴乙与丙也不相似.
故选:C.
9.解:设这棵树高度为hm,
∵同一时刻物高与影长成正比,
∴=,
解得:h=4.8.
故选:B.
10.解:A、形状、大小相同的两个三角形全等,本选项说法错误;
B、面积相等的两个三角形不一定全等,本选项说法错误;
C、两个全等图形形状一定相同,本选项说法正确;
D、边长相等的两个正方形一定是全等图形,本选项说法错误;
故选:C.
二.填空题(共10小题)
11.解:△PMF∽△AMC;△AMC∽△ABP;△PMF∽△ABP;△BDN∽△PEN,
∵平行四边形CDEF,
∴EF∥AB,CF∥ED,
∴∠F=∠MCA,∠FPM=∠A,
∴△PMF∽△AMC;
∵∠A=∠A,∠ACM=∠ADE=∠APB,
∴△AMC∽△ABP;
∵∠F=∠ACM=∠APB,∠FPM=∠A,
∴△PMF∽△ABP;
∵EF∥AB,
∴∠E=∠NDB,∠EPN=∠B,
∴△BDN∽△PEN.
故答案为:△PMF∽△AMC;△AMC∽△ABP;△PMF∽△ABP;△BDN∽△PEN
12.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABE=∠FDE,∠EAB=∠EFD,
∴△ABE∽△FDE,
∴①,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠GBE=∠ADE,∠G=∠DEA,
∴△BEG∽△DEA,
∴②,
由①②可得,,
∵AE=4,EG=3,
∴EF=.
故答案为:.
13.解:同一底片印出来的不同尺寸的照片,形状相同,但大小不同,∴是相似图形.
14.解:一个六边形的边长依次为1,2,3,4,5,6,7,8.
与它相似的另一个多边形最大边长为12,
则这个多边形的周长是36,相似比是8:12=2:3,
根据周长之比等于相似比,
因而设另一个多边形的周长是x,
则36:x=2:3,
解得:x=54
另一个多边形的周长为54.
故答案为:54.
15.解:若△ABC∽△BDC,
则∠C=∠C,∠CBD=∠A=36°,
∵BD是角平分线,
∴∠ABC=72°,
∴∠C=180°﹣∠A﹣∠ABC=72°,
故答案为:72°
16.解:∵△ABC∽△DEF,AB=21cm,DE=28cm,
∴△ABC和△DEF的相似比为:AB:DE=21:28=3:4.
故答案为:3:4.
17.解:∵两个相似多边形的周长之比为2:3,
∴其相似比为:2:3,
∴它们的面积比为:4:9,
设两个相似多边形的面积分别为:4x,9x,
∵面积之差为12,
∴9x﹣4x=12,
解得:x=2.4,
∴两个相似多边形的面积分别是:9.6,21.6.
故答案为:9.6,21.6.
18.解:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴=,
∵DE=40cm,EF=20cm,AC=150cm,CD=80cm,
∴=,
∴BC=40cm,
∴AB=AC+BC=150+400=550cm,
故答案为:550.
19.解:分两种情况:
(1)Q在AC边上时,如图1,过B作BG⊥AC于G,过P作PF⊥AC于F,
S△QPC=QC?PF,S△ABC=AC?BG,
∵=,
∴=,
∵PF∥BG,
∴=,
∴=,
∴QC=6,
∴AQ=AC﹣QC=8﹣6=2;
(2)Q在AB边上时,如图2,过P作PE⊥AB于E,过C作CF⊥AB于F,
S△BQP=BQ?PE,S△ABC=AB?CF,
∵=,
∴=,
∵PE∥CF,
∴=,
∴,
∴BQ=,
∴AQ=AB﹣BQ=12﹣=7.5,
综上所述:AQ的长为2或7.5.
20.解:∵五边形ABCDE∽五边形A′B′C′D′E′,
∴∠B=∠B′=130°,∠D=∠D′=85°,
又∵五边形的内角和为540°,
∴∠E=540°﹣∠A﹣∠B﹣∠C﹣∠D=100°,
故答案为:100°.
三.解答题(共7小题)
21.解:根据边长计算,所画图形如下所示:
22.解:∵△ABC与△ADB相似,
∴△ABC∽△ADB,
∴=,
∴AB2=AC?AD=10×4=40,
∴△ABC与△ADB的相似比为==.
23.解:根据位似图形的定义得出:
小Q对,①,②都可以看成位似变换,位似中心分别为O、A,
③、④虽然都存在相似三角形,但对应顶点的连线不相交于一点,而且对应边也不平行,所以③、④不是位似变换.
24.解:观察比较图形,根据相似形的定义可知:
与图形(1)相似的有a;
与图形(2)相似的有d;
与图形(3)相似的有g.
25.解:∵AB⊥BD,CD⊥BD,
∴∠ABD+∠BDC=180°,
∴AB∥CD,
∵EF⊥BD,
∴EF∥AB∥CD,
∴∠EFD=∠ABD,∠DEF=∠DAB,
∴△DEF∽△DAB;
∵∠BFE=∠BDC,∠BEF=∠BCD,
∴△BEF∽△BCD;
∵∠A=∠EDC,∠ABE=∠C,
∴△ABE∽△DEC,
故答案为:DAB;BCD;DCE.
26.解:△OA′B′就是所求的三角形,O(0,0),A′(2,4),B′(4,0).
或O(0,0),A′′(﹣2,﹣4),B′(﹣4,0).
27.解:∵AD=2BD,S△ABC=6,
∴S△ADC=S△ABC=4,S△BDC=S△ABC=2.
过E作EG∥AB交CD于G,
∵BE=CE,
∴CG=DG,
∴BD=2EG,
∵AD=2BD,
∴AD=4EG.
设S△EGF=x.
∵EG∥BD,
∴△CEG∽△CBD,
∴S△CEG:
S△CBD=()2=,
∴S△CEG=S△CBD=×2=,S梯形EGDB=2﹣=,
设S△FEG=x,则S四边形BEFD=﹣x,
∵S△ABE=S△ABC=3,
∴S△ADF=S△ABE﹣S四边形BEFD=3﹣(﹣x)=+x.
∵EG∥AD,
∴△FEG∽△FAD,
∴S△FEG:S△FAD=()2=,
∴S△FAD=16S△FEG=16x,
∴16x=+x,
解得x=,
∴S四边形BEFD=﹣x=﹣=.
图形的相似》单元测试卷
一.选择题(共10小题)
1.下列语句中的图形必成相似形的是( )
A.只有一个角为30°的等腰三角形
B.邻边之比为2的两个平行四边形
C.底角为40°的两个等腰梯形
D.有一个角为40°的两个等腰梯形
2.如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )
A.∠AED=∠B
B.∠ADE=∠C
C.
D.
3.如图,正方形ABCD的面积为1,M是AB的中点,连接CM、DM、AC,则图中阴影部分的面积为( )
A.
B.
C.
D.
4.在某一时刻测得1米高的竹竿的影长为0.9米,同时测得一棵树的影长,落在地面上的影长为1.8米,落在墙上的影长为0.4米,则这棵树的高度为( )
A.2米
B.2.4米
C.2.2米
D.2.8米
5.△ABC∽△A′B′C′,已知AB=5,A′B′=6,△ABC面积为10,那么另一个三角形的面积为( )
A.15
B.14.4
C.12
D.10.8
6.已知五边形ABCDE与五边形A1B1C1D1E1是两个位似的图形,它们面积的比为4:9,若位似中心O到A的距离为6,则O到A的对应点A1的距离为( )
A.4
B.
C.9
D.
7.如图,两个位似图形△ABO和△A′B′O,若OA:OA′=3:1,则正确的是( )
A.AB:A′B′=3:1
B.AA′:BB′=AB:AB′
C.OA:OB′=2:1
D.∠A=∠B′
8.如图所示,图中的三个矩形中相似的是( )
A.甲、乙和丙
B.甲和乙
C.甲和丙
D.乙和丙
9.张华同学的身高为160厘米,某一时刻他在阳光下的影子长为200厘米,与他相邻近的一棵树的影子长为6米,则这棵树的高为( )米.
A.3.2
B.4.8
C.5.2
D.5.6
10.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.两个全等图形形状一定相同
D.两个正方形一定是全等图形
二.填空题(共10小题)
11.如图,C、D是△PAB的边AB上的两点,以CD为边作平行四边形CDEF,EF经过点P,且
∠APB=∠ADE.试写出四对相似三角形
.
12.如图,平行四边形ABCD中,E是BD上一点,AE的延长线与BC的延长线交于F,与CD交于G,若AE=4,EG=3,则EF=
.
13.同一底片印出来的不同尺寸的照片也是
.
14.一个多边形的边长依次为1,2,3,4;5,6,7,8,与它位似的另一个多边形的最大边长为12,那么另一个多边形的周长为
.
15.如图,在△ABC中,∠A=36°,BD是角平分线,当∠C=
°时,△ABC∽△BDC.
16.已知△ABC∽△DEF,AB=21cm,DE=28cm,则△ABC和△DEF的相似比为
.
17.两个相似多边形的周长之比为2:3,而面积之差为12,则两个相似多边形的面积分别是
.
18.如图,小明同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶点B在同一直线上.已知纸板的两条直角边DE=40cm,EF=20cm,测得边DF离地面的高度DM=150cm,CD=800cm,则树高AB=
cm.
19.△ABC中,AB=12,AC=8,P是BC上的一点,且BP=2PC,设Q是△ABC某边上的一点,如果PQ截得的三角形与原三角形相似,且它们的面积比是1:4,则AQ的长为
.
20.五边形ABCDE∽五边形A′B′C′D′E′,∠A=120°,∠B′=130°,∠C=105°,∠D′=85°,则∠E=
.
三.解答题(共7小题)
21.以下列正方形网格的交点为顶点,分别画出两个相似比不为1的相似三角形,使它们:
(1)都是直角三角形;(2)都是锐角三角形;(3)都是钝角三角形.
22.如图,△ABC与△ADB相似,AD=4,CD=6,求这两个三角形的相似比.
23.如图是几组三角形的组合图形,图①中,△AOB∽△DOC;图②中,△ABC∽△ADE;图③中,△ABC∽△ACD;图④中,△ACD∽△CBD.
小Q说:图①、②是位似变换,其位似中心分别是O和A.
小R说:图③、④是位似变换,其位似中心是点D.
请你观察一番,评判小Q,小R谁对谁错.
24.观察下列的图形(a)﹣(g),其中哪些是与图形(1)、(2)或(3)相似的.
与图形(1)相似的有
;(填序号)
与图形(2)相似的有
;
与图形(3)相似的有
.
25.如图,已知AB⊥BD,CD⊥BD,垂足分别为B、D,AD与BC相交于点E,EF⊥BD,垂足为F,试回答图中,△DEF∽△
,△BEF∽△
,△ABE∽△
.
26.画图:点A(1,2),B(2,0)把△ABO以点O为位似中心放大到原来的2倍,且写出对应顶点的坐标.
27.如图,D,E分别是△ABC边AB,BC上的点,AD=2BD,BE=CE,AE与CD相交于点F,若S△ABC=6,求四边形BEFD的面积.
参考答案与试题解析
一.选择题(共10小题)
1.解:A、只有一个角为30°的等腰三角形,30°的角必定是顶角,所以,底角也一定相等,三角形相似,故本选项正确;
B、邻边之比为2,夹角不一定相等,两平行四边形不一定相似,故本选项错误;
C、底角为40°的等腰梯形,角对应相等,边不一定对应成比例,两等腰梯形不一定相似,故本选项错误;
D、有一个角为40°的等腰梯形,角对应相等,边不一定对应成比例,两等腰梯形不一定相似,故本选项错误.
故选:A.
2.解:A、∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故A选项错误;
B、∠ADE=∠C,∠A=∠A,则可判断△ADE∽△ACB,故B选项错误;
C、=不能判定△ADE∽△ACB,故B选项正确;
D、=,且夹角∠A=∠A,能确定△ADE∽△ACB,故D选项错误.
故选:C.
3.解:如图,过点E作HF⊥AB
∵AM∥CD,
∴∠DCE=∠EAM,∠CDE=∠EMA,
∴△AME∽△CDE
∴AM:DC=EH:EF=1:2,FH=AD=1
∴EH=,EF=.
∴阴影部分的面积=S正﹣S△AME﹣S△CDE﹣S△MBC=1﹣﹣﹣=.
故选:B.
4.解:设影长为1.8m时树的高度为hm,
∵在某一时刻测得直立的标杆长0.9m,其影长为1m,
∴,
解得x=2m,
∴树的高度=2+0.4=2.4m,
答:树的高度是2.4米.
故选:B.
5.解:∵△ABC∽△A′B′C′,AB=5,A′B′=6,
∴=,
∵△ABC面积为10,
∴解得:S△A′B′C′=14.4.
故选:B.
6.解:设点O到A1的距离为x,
∵它们面积的比为4:9,
∴(6:x)2=4:9,
解得x=9,
即:O到A的对应点A1的距离为9.
故选:C.
7.解:∵△ABO和△A′B′O是位似图形,
∴△ABO∽△A′B′O,
∴OA:OA′=AB:A′B′=3:1(A正确),
∠A=∠A′(D不正确),
B,C均无法证得.
故选:A.
8.解:∵都是矩形,
∴所有对应角相等;
∵甲与乙:≠,故不相似;
甲与丙:,故相似;
∴乙与丙也不相似.
故选:C.
9.解:设这棵树高度为hm,
∵同一时刻物高与影长成正比,
∴=,
解得:h=4.8.
故选:B.
10.解:A、形状、大小相同的两个三角形全等,本选项说法错误;
B、面积相等的两个三角形不一定全等,本选项说法错误;
C、两个全等图形形状一定相同,本选项说法正确;
D、边长相等的两个正方形一定是全等图形,本选项说法错误;
故选:C.
二.填空题(共10小题)
11.解:△PMF∽△AMC;△AMC∽△ABP;△PMF∽△ABP;△BDN∽△PEN,
∵平行四边形CDEF,
∴EF∥AB,CF∥ED,
∴∠F=∠MCA,∠FPM=∠A,
∴△PMF∽△AMC;
∵∠A=∠A,∠ACM=∠ADE=∠APB,
∴△AMC∽△ABP;
∵∠F=∠ACM=∠APB,∠FPM=∠A,
∴△PMF∽△ABP;
∵EF∥AB,
∴∠E=∠NDB,∠EPN=∠B,
∴△BDN∽△PEN.
故答案为:△PMF∽△AMC;△AMC∽△ABP;△PMF∽△ABP;△BDN∽△PEN
12.证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABE=∠FDE,∠EAB=∠EFD,
∴△ABE∽△FDE,
∴①,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠GBE=∠ADE,∠G=∠DEA,
∴△BEG∽△DEA,
∴②,
由①②可得,,
∵AE=4,EG=3,
∴EF=.
故答案为:.
13.解:同一底片印出来的不同尺寸的照片,形状相同,但大小不同,∴是相似图形.
14.解:一个六边形的边长依次为1,2,3,4,5,6,7,8.
与它相似的另一个多边形最大边长为12,
则这个多边形的周长是36,相似比是8:12=2:3,
根据周长之比等于相似比,
因而设另一个多边形的周长是x,
则36:x=2:3,
解得:x=54
另一个多边形的周长为54.
故答案为:54.
15.解:若△ABC∽△BDC,
则∠C=∠C,∠CBD=∠A=36°,
∵BD是角平分线,
∴∠ABC=72°,
∴∠C=180°﹣∠A﹣∠ABC=72°,
故答案为:72°
16.解:∵△ABC∽△DEF,AB=21cm,DE=28cm,
∴△ABC和△DEF的相似比为:AB:DE=21:28=3:4.
故答案为:3:4.
17.解:∵两个相似多边形的周长之比为2:3,
∴其相似比为:2:3,
∴它们的面积比为:4:9,
设两个相似多边形的面积分别为:4x,9x,
∵面积之差为12,
∴9x﹣4x=12,
解得:x=2.4,
∴两个相似多边形的面积分别是:9.6,21.6.
故答案为:9.6,21.6.
18.解:∵∠DEF=∠BCD=90°∠D=∠D
∴△DEF∽△DCB
∴=,
∵DE=40cm,EF=20cm,AC=150cm,CD=80cm,
∴=,
∴BC=40cm,
∴AB=AC+BC=150+400=550cm,
故答案为:550.
19.解:分两种情况:
(1)Q在AC边上时,如图1,过B作BG⊥AC于G,过P作PF⊥AC于F,
S△QPC=QC?PF,S△ABC=AC?BG,
∵=,
∴=,
∵PF∥BG,
∴=,
∴=,
∴QC=6,
∴AQ=AC﹣QC=8﹣6=2;
(2)Q在AB边上时,如图2,过P作PE⊥AB于E,过C作CF⊥AB于F,
S△BQP=BQ?PE,S△ABC=AB?CF,
∵=,
∴=,
∵PE∥CF,
∴=,
∴,
∴BQ=,
∴AQ=AB﹣BQ=12﹣=7.5,
综上所述:AQ的长为2或7.5.
20.解:∵五边形ABCDE∽五边形A′B′C′D′E′,
∴∠B=∠B′=130°,∠D=∠D′=85°,
又∵五边形的内角和为540°,
∴∠E=540°﹣∠A﹣∠B﹣∠C﹣∠D=100°,
故答案为:100°.
三.解答题(共7小题)
21.解:根据边长计算,所画图形如下所示:
22.解:∵△ABC与△ADB相似,
∴△ABC∽△ADB,
∴=,
∴AB2=AC?AD=10×4=40,
∴△ABC与△ADB的相似比为==.
23.解:根据位似图形的定义得出:
小Q对,①,②都可以看成位似变换,位似中心分别为O、A,
③、④虽然都存在相似三角形,但对应顶点的连线不相交于一点,而且对应边也不平行,所以③、④不是位似变换.
24.解:观察比较图形,根据相似形的定义可知:
与图形(1)相似的有a;
与图形(2)相似的有d;
与图形(3)相似的有g.
25.解:∵AB⊥BD,CD⊥BD,
∴∠ABD+∠BDC=180°,
∴AB∥CD,
∵EF⊥BD,
∴EF∥AB∥CD,
∴∠EFD=∠ABD,∠DEF=∠DAB,
∴△DEF∽△DAB;
∵∠BFE=∠BDC,∠BEF=∠BCD,
∴△BEF∽△BCD;
∵∠A=∠EDC,∠ABE=∠C,
∴△ABE∽△DEC,
故答案为:DAB;BCD;DCE.
26.解:△OA′B′就是所求的三角形,O(0,0),A′(2,4),B′(4,0).
或O(0,0),A′′(﹣2,﹣4),B′(﹣4,0).
27.解:∵AD=2BD,S△ABC=6,
∴S△ADC=S△ABC=4,S△BDC=S△ABC=2.
过E作EG∥AB交CD于G,
∵BE=CE,
∴CG=DG,
∴BD=2EG,
∵AD=2BD,
∴AD=4EG.
设S△EGF=x.
∵EG∥BD,
∴△CEG∽△CBD,
∴S△CEG:
S△CBD=()2=,
∴S△CEG=S△CBD=×2=,S梯形EGDB=2﹣=,
设S△FEG=x,则S四边形BEFD=﹣x,
∵S△ABE=S△ABC=3,
∴S△ADF=S△ABE﹣S四边形BEFD=3﹣(﹣x)=+x.
∵EG∥AD,
∴△FEG∽△FAD,
∴S△FEG:S△FAD=()2=,
∴S△FAD=16S△FEG=16x,
∴16x=+x,
解得x=,
∴S四边形BEFD=﹣x=﹣=.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
