人教版八年级上册数学13.4专题:最短路径问题复习 课件(16张PPT)
文档属性
| 名称 | 人教版八年级上册数学13.4专题:最短路径问题复习 课件(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 412.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 19:41:14 | ||
图片预览



文档简介
1
13章:最短路径问题复习
2
1.最短路径问题的类型
(一)两点一线型的线段和最小值问题;
①两点在直线异侧
②两点在直线同侧
(二)两线一点型线段和最小值问题;
(三)两点两线型的线段和最小值问题;
(四)造桥选址问题.
3
2. 解决最短路径问题的方法:
借助 或平移的知识,化折为直,利用“ ”或“ ”来求线段和的最小值.
轴对称
两点之间,线段最短
垂线段最短
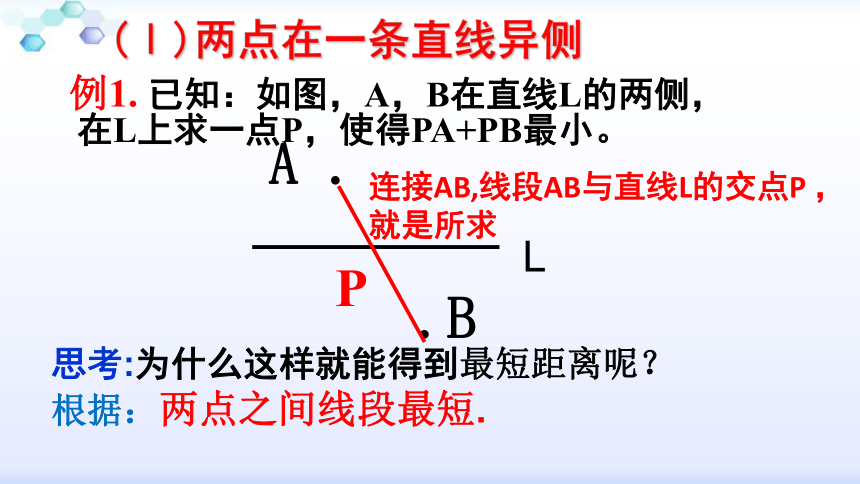
(Ⅰ)两点在一条直线异侧
例1. 已知:如图,A,B在直线L的两侧,在L上求一点P,使得PA+PB最小。
A .
.B
P
思考:为什么这样就能得到最短距离呢?
根据:两点之间线段最短.
连接AB,线段AB与直线L的交点P ,就是所求
L
5
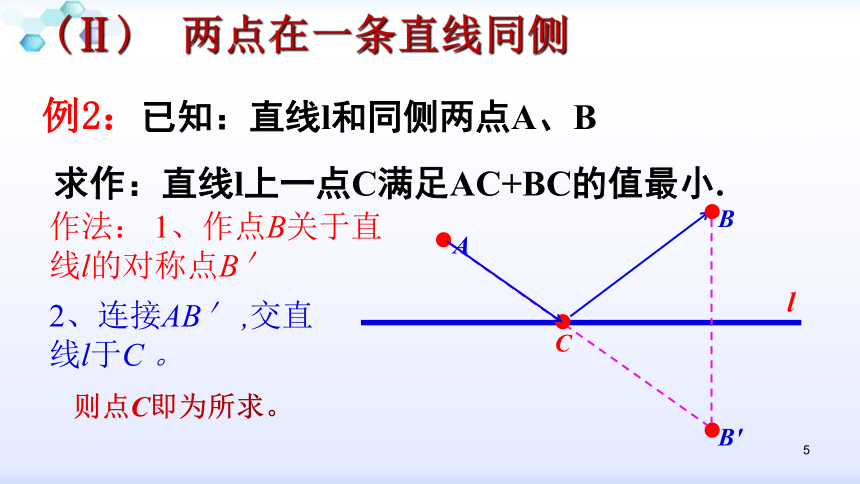
例2:已知:直线l和同侧两点A、B
求作:直线l上一点C满足AC+BC的值最小.
A
C
l
B
作法: 1、作点B关于直线l的对称点B'
2、连接AB' ,交直线l于C 。
则点C即为所求。
B′
(Ⅱ) 两点在一条直线同侧
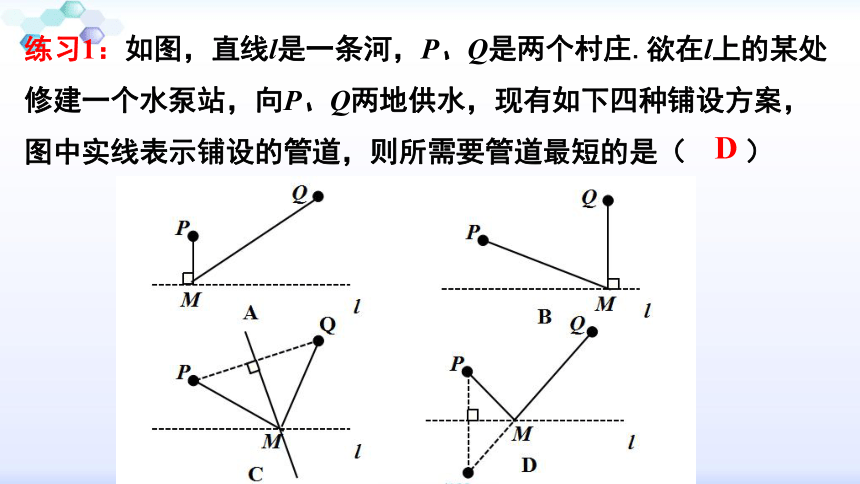
练习1:如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需要管道最短的是( )
D
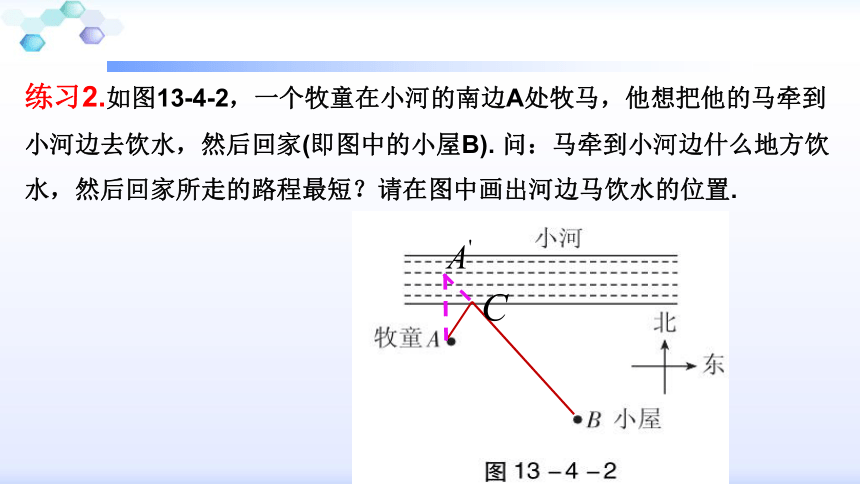
练习2.如图13-4-2,一个牧童在小河的南边A处牧马,他想把他的马牵到小河边去饮水,然后回家(即图中的小屋B). 问:马牵到小河边什么地方饮水,然后回家所走的路程最短?请在图中画出河边马饮水的位置.
练习3. 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
A.7.5 B.5
C.4 D.不能确定
解析:△ABC为等边三角形,点D是BC边的中点,即点B与点C关于直线AD对称.∵点F在AD上,故BF=CF.即BF+EF的最小值可转化为求CF+EF的最小值,故连接CE即可,线段CE的长即为BF+EF的最小值.
B
9
变式.如图,△ABC是等边三角形,高AD=3,点E是AB上中点,点P是AD上的动点,则PE+PB的最小值为 .
A
B
E
C
∟
P
D
3
10
学以致用
练习4.在所给网格图(每小格均为边长是1的正方形)中完成下列各题(用直尺画图):(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PB1+PC最小;
(3)在DE上画出点Q,使QA+QC最小
知识点三:利用轴对称和垂线段最短解决最小值问题
A
B
E
C
D
11
典例讲评
知识点一:利用轴对称解决最短路径问题
例3:如图,已知点A是锐角∠MON内的一点,试分别在OM,ON上确定点B,C,使△ABC的周长最小,写出你作图的主要步骤,并标明你所确定的点.(要求画出草图,保留作图痕迹)
作法: 1、分别作点A关于OM、ON的对称点A′,A′′;
2、连接A′A′′ ,分别交OM、ON于B、C ;
则点B、C即为所求。
O
M
N
∟
∟
A
A′
A′′
B
C
两线一点型
12
学以致用
练习7.如图,OA,OB分别是线段MC,MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点处,则小蚂蚁爬行的路径最短可为( )
A. 12cm B 10cm C. 7cm D. 5cm
B
知识点一:利用轴对称解决最短路径问题
两线一点型
O
A
B
∟
∟
M
C
D
E
F
13
典例讲评
知识点一:利用轴对称解决最短路径问题
例4:某中学八(12)班举行文艺晚会,桌子摆成如图所示两直排(图中的AO,BO),AO桌面上摆满了橘子,OB桌面上摆满了糖果,站在C处的学生小明先拿橘子再拿糖果,然后到D处座位上,请你帮助他设计一条行走路线,使其所走的总程最短.
两线两点型
O
M
A
C
A′
D
B
C
N
2. 如图:C为马厩,D为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线。
作法:1.作点C关于直线
OA的对称点点F,
2.作点D关于直线OB
的对称点点E,
3.连接EF分别交直线OA.OB于点G.H,
则CG+GH+DH最短
F
A
O
B
D ·
· C
E
G
H
15
完成作业2.24作业
16
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
13章:最短路径问题复习
2
1.最短路径问题的类型
(一)两点一线型的线段和最小值问题;
①两点在直线异侧
②两点在直线同侧
(二)两线一点型线段和最小值问题;
(三)两点两线型的线段和最小值问题;
(四)造桥选址问题.
3
2. 解决最短路径问题的方法:
借助 或平移的知识,化折为直,利用“ ”或“ ”来求线段和的最小值.
轴对称
两点之间,线段最短
垂线段最短
(Ⅰ)两点在一条直线异侧
例1. 已知:如图,A,B在直线L的两侧,在L上求一点P,使得PA+PB最小。
A .
.B
P
思考:为什么这样就能得到最短距离呢?
根据:两点之间线段最短.
连接AB,线段AB与直线L的交点P ,就是所求
L
5
例2:已知:直线l和同侧两点A、B
求作:直线l上一点C满足AC+BC的值最小.
A
C
l
B
作法: 1、作点B关于直线l的对称点B'
2、连接AB' ,交直线l于C 。
则点C即为所求。
B′
(Ⅱ) 两点在一条直线同侧
练习1:如图,直线l是一条河,P、Q是两个村庄.欲在l上的某处修建一个水泵站,向P、Q两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需要管道最短的是( )
D
练习2.如图13-4-2,一个牧童在小河的南边A处牧马,他想把他的马牵到小河边去饮水,然后回家(即图中的小屋B). 问:马牵到小河边什么地方饮水,然后回家所走的路程最短?请在图中画出河边马饮水的位置.
练习3. 如图,已知点D、点E分别是等边三角形ABC中BC、AB边的中点,AD=5,点F是AD边上的动点,则BF+EF的最小值为( )
A.7.5 B.5
C.4 D.不能确定
解析:△ABC为等边三角形,点D是BC边的中点,即点B与点C关于直线AD对称.∵点F在AD上,故BF=CF.即BF+EF的最小值可转化为求CF+EF的最小值,故连接CE即可,线段CE的长即为BF+EF的最小值.
B
9
变式.如图,△ABC是等边三角形,高AD=3,点E是AB上中点,点P是AD上的动点,则PE+PB的最小值为 .
A
B
E
C
∟
P
D
3
10
学以致用
练习4.在所给网格图(每小格均为边长是1的正方形)中完成下列各题(用直尺画图):(1)画出格点△ABC(顶点均在格点上)关于直线DE对称的△A1B1C1;
(2)在DE上画出点P,使PB1+PC最小;
(3)在DE上画出点Q,使QA+QC最小
知识点三:利用轴对称和垂线段最短解决最小值问题
A
B
E
C
D
11
典例讲评
知识点一:利用轴对称解决最短路径问题
例3:如图,已知点A是锐角∠MON内的一点,试分别在OM,ON上确定点B,C,使△ABC的周长最小,写出你作图的主要步骤,并标明你所确定的点.(要求画出草图,保留作图痕迹)
作法: 1、分别作点A关于OM、ON的对称点A′,A′′;
2、连接A′A′′ ,分别交OM、ON于B、C ;
则点B、C即为所求。
O
M
N
∟
∟
A
A′
A′′
B
C
两线一点型
12
学以致用
练习7.如图,OA,OB分别是线段MC,MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点处,则小蚂蚁爬行的路径最短可为( )
A. 12cm B 10cm C. 7cm D. 5cm
B
知识点一:利用轴对称解决最短路径问题
两线一点型
O
A
B
∟
∟
M
C
D
E
F
13
典例讲评
知识点一:利用轴对称解决最短路径问题
例4:某中学八(12)班举行文艺晚会,桌子摆成如图所示两直排(图中的AO,BO),AO桌面上摆满了橘子,OB桌面上摆满了糖果,站在C处的学生小明先拿橘子再拿糖果,然后到D处座位上,请你帮助他设计一条行走路线,使其所走的总程最短.
两线两点型
O
M
A
C
A′
D
B
C
N
2. 如图:C为马厩,D为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边饮马,然后回到帐篷,请你帮他确定这一天的最短路线。
作法:1.作点C关于直线
OA的对称点点F,
2.作点D关于直线OB
的对称点点E,
3.连接EF分别交直线OA.OB于点G.H,
则CG+GH+DH最短
F
A
O
B
D ·
· C
E
G
H
15
完成作业2.24作业
16
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?
蓦然回首
