人教版数学九年级上册 24.1圆的有关性质同步测试试题(一)(Word版 含解析)
文档属性
| 名称 | 人教版数学九年级上册 24.1圆的有关性质同步测试试题(一)(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 375.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 00:00:00 | ||
图片预览

文档简介
圆同步测试试题(一)
一.选择题
1.如图,A,B,C三点在⊙O上,若∠ACB=120°,则∠AOB的度数是( )
A.60° B.90° C.100° D.120°
2.如图,AB是⊙O的直径,若∠BAC=20°,则∠ADC=( )
A.40° B.60° C.70° D.80°
3.如图,圆的两条弦AB,CD相交于点E,且,∠A=35°,则且∠CEB的度数为( )
A.50° B.80° C.70° D.90°
4.下面说法正确的是( )
A.一条路已经修了80%千米
B.半径是2厘米的圆,它的周长和面积相等
C.某班的出勤率达到101%
D.某校的男同学人数比女同学人数多10%
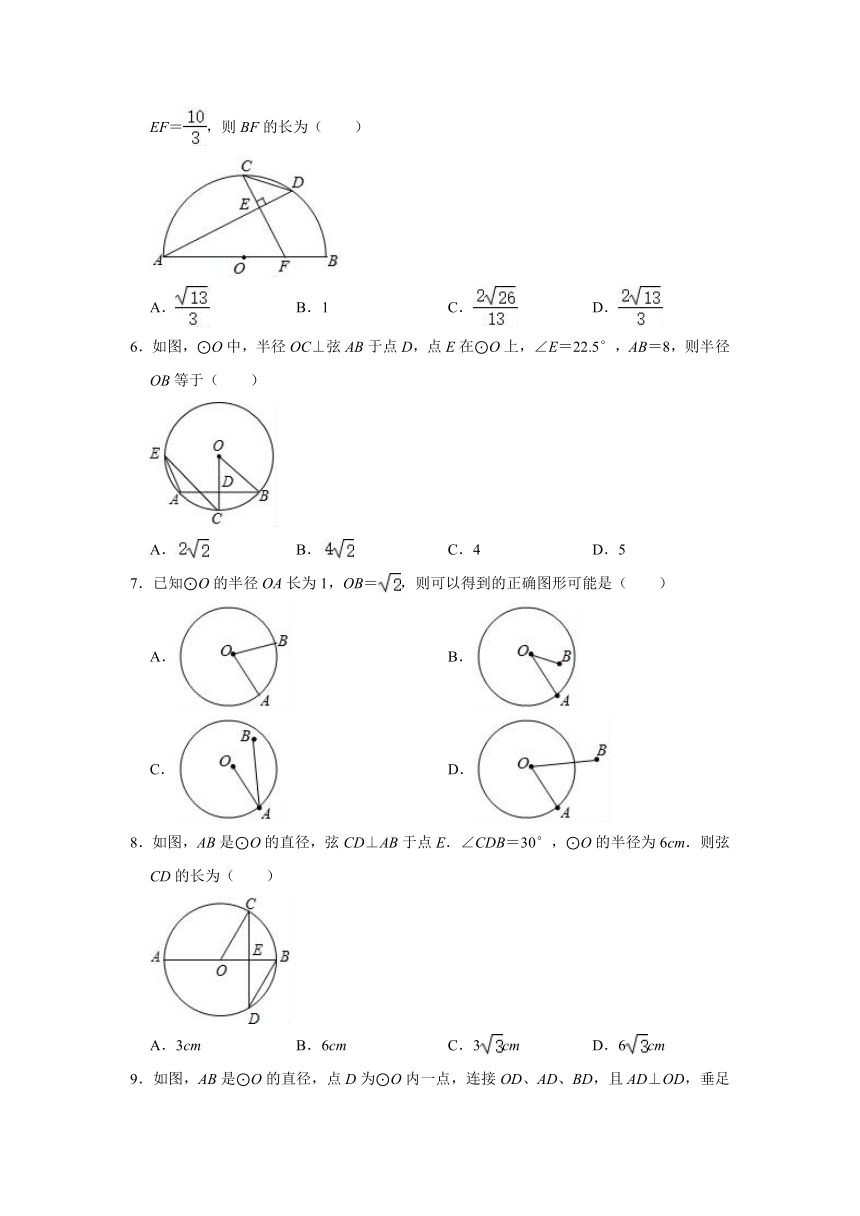
5.如图,点C是半圆O的中点,AB是直径,CF⊥弦AD于点E,交AB于点F,若CE=1,EF=,则BF的长为( )
A. B.1 C. D.
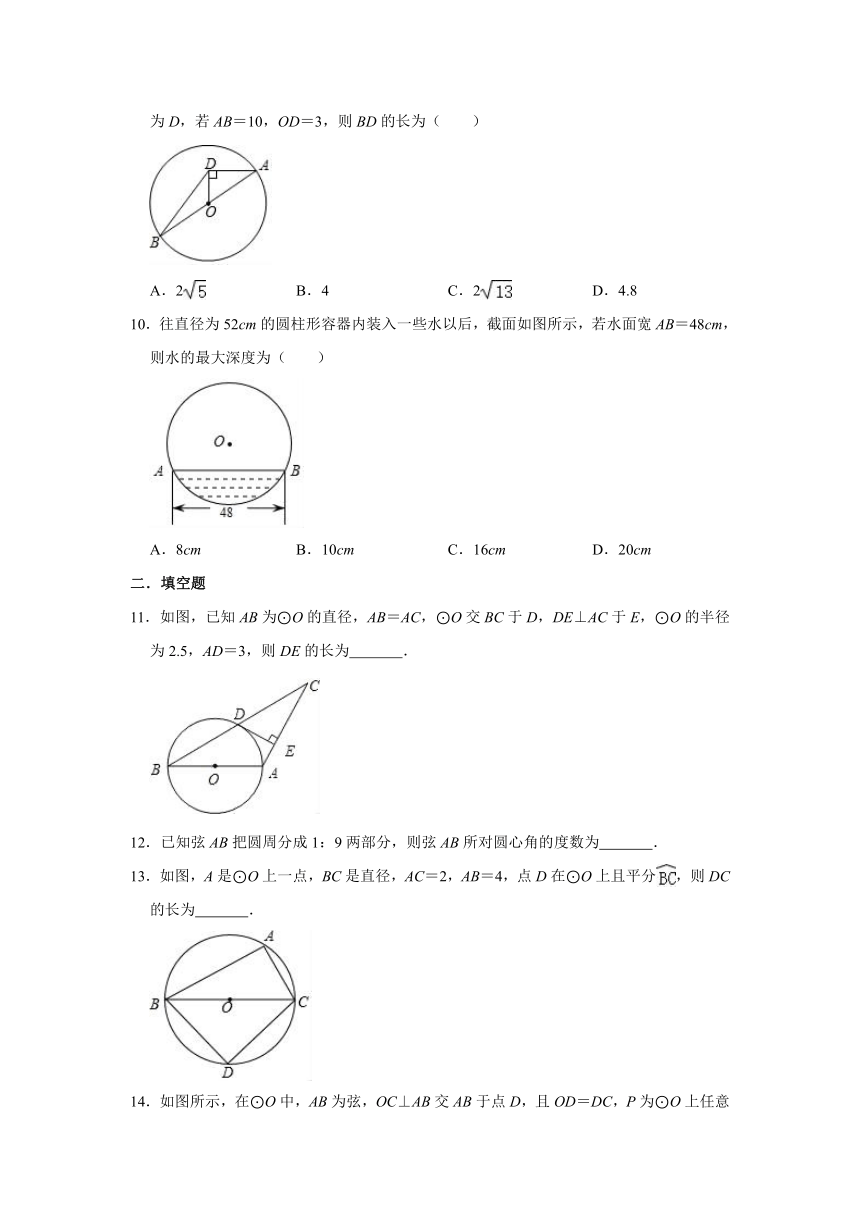
6.如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=8,则半径OB等于( )
A. B. C.4 D.5
7.已知⊙O的半径OA长为1,OB=,则可以得到的正确图形可能是( )
A. B.
C. D.
8.如图,AB是⊙O的直径,弦CD⊥AB于点E.∠CDB=30°,⊙O的半径为6cm.则弦CD的长为( )
A.3cm B.6cm C.3cm D.6cm
9.如图,AB是⊙O的直径,点D为⊙O内一点,连接OD、AD、BD,且AD⊥OD,垂足为D,若AB=10,OD=3,则BD的长为( )
A.2 B.4 C.2 D.4.8
10.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
二.填空题
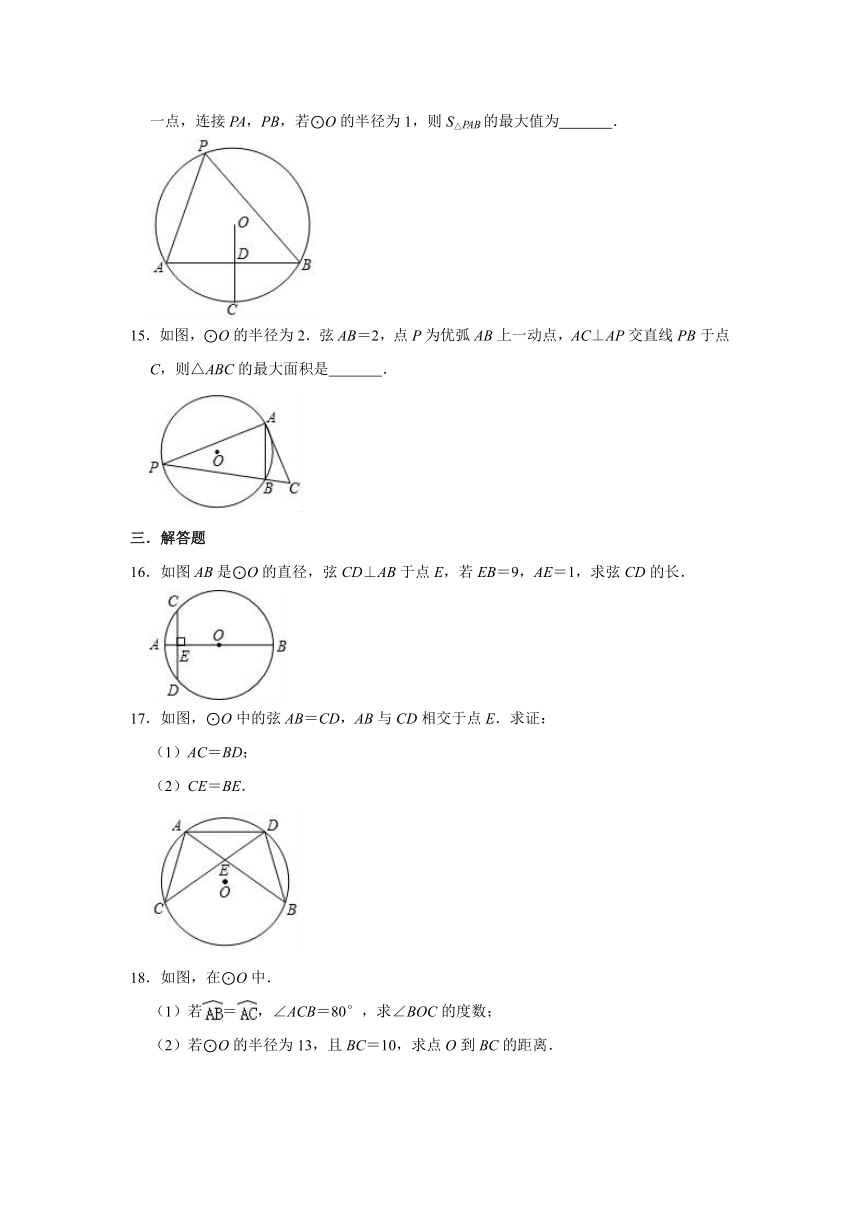
11.如图,已知AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC于E,⊙O的半径为2.5,AD=3,则DE的长为 .
12.已知弦AB把圆周分成1:9两部分,则弦AB所对圆心角的度数为 .
13.如图,A是⊙O上一点,BC是直径,AC=2,AB=4,点D在⊙O上且平分,则DC的长为 .
14.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D,且OD=DC,P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则S△PAB的最大值为 .
15.如图,⊙O的半径为2.弦AB=2,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是 .
三.解答题
16.如图AB是⊙O的直径,弦CD⊥AB于点E,若EB=9,AE=1,求弦CD的长.
17.如图,⊙O中的弦AB=CD,AB与CD相交于点E.求证:
(1)AC=BD;
(2)CE=BE.
18.如图,在⊙O中.
(1)若=,∠ACB=80°,求∠BOC的度数;
(2)若⊙O的半径为13,且BC=10,求点O到BC的距离.
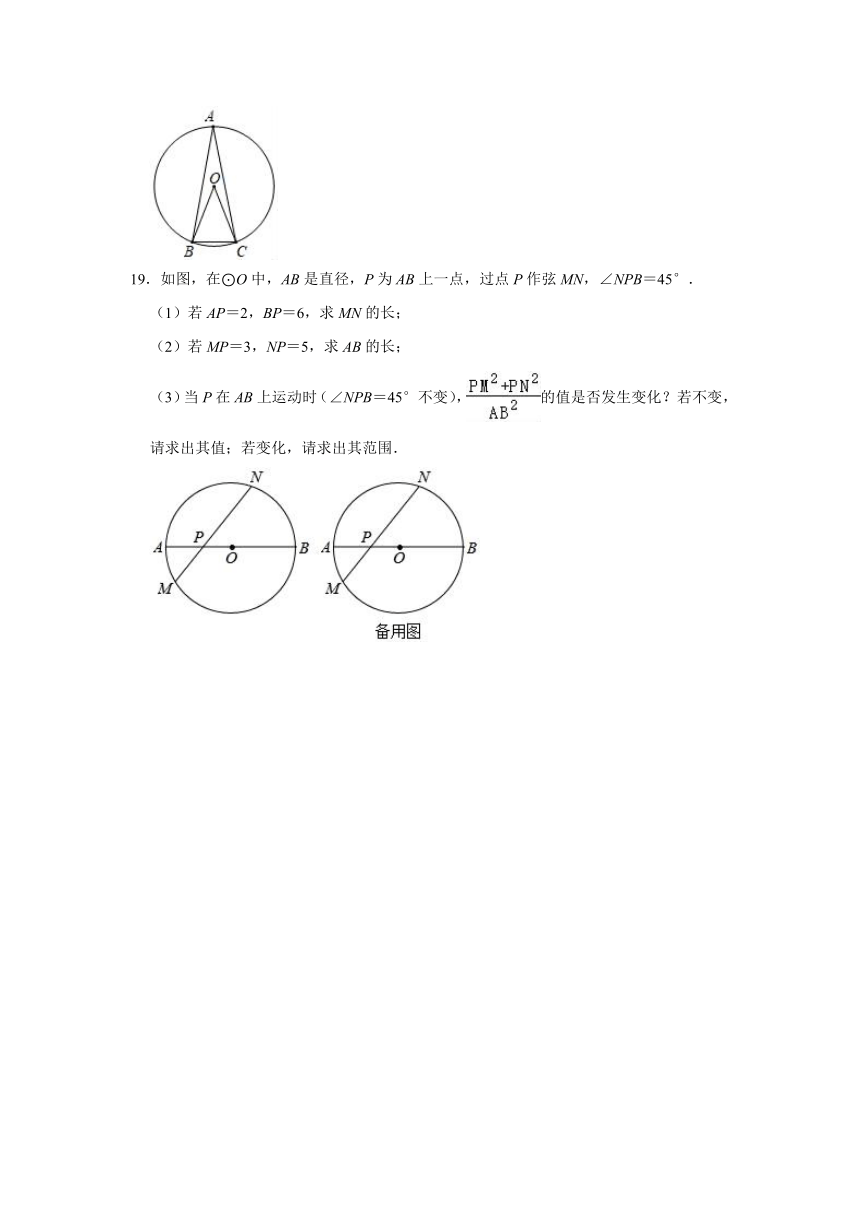
19.如图,在⊙O中,AB是直径,P为AB上一点,过点P作弦MN,∠NPB=45°.
(1)若AP=2,BP=6,求MN的长;
(2)若MP=3,NP=5,求AB的长;
(3)当P在AB上运动时(∠NPB=45°不变),的值是否发生变化?若不变,请求出其值;若变化,请求出其范围.
参考答案与试题解析
一.选择题
1.【解答】解:如图,在优弧AB上取一点D,连接AD,BD.
∵∠ACB+∠ADB=180°,∠ACB=120°,
∴∠ADB=60°,
∴∠AOB=2∠ADB=120°,
故选:D.
2.【解答】解:∵AB是直径,
∴∠ACB=90°,
∵∠BAC=20°,
∴∠ABC=90°﹣20°=70°,
∴∠ADC=∠ABC=70°,
故选:C.
3.【解答】解:∴=,
∴∠C=∠A=35°,
∴∠CEB=∠A+∠C=35°+35°=70°.
故选:C.
4.【解答】解:A:根据百分数意义,百分数表示一个数是另一个数的百分之几,不能表示具体数量,无单位,故错误;
B:圆的周长单位是厘米,面积单位是平方厘米,两者之间无法比较大小,故错误;
C:出勤率最高为100%,不可能更大了,因此选项错误;
故选:D.
5.【解答】解:如图,连接AC,BC,OC,过点B作BH⊥CF交CF的延长线于H,设OC交AD于J.
∵=,
∴AC=BC,OC⊥AB,
∵AB是直径,
∴ACB=90°,
∴∠ACJ=∠CBF=45°,
∵CF⊥AD,
∴∠ACF+∠CAJ=90°,∠ACF+∠BCF=90°,
∴∠CAJ=∠BCF,
∴△CAJ≌△BCF(ASA),
∴CJ=BF,AJ=CF=1+=,
∵OC=OB,
∴OJ=OF,设BF=CJ=x.OJ=OF=y,
∵∠AEC=∠H=90°,∠CAE=∠BCH,CA=CB,
∴△ACE≌△CBH(AAS),
∴EC=BH=1,
∵∠ECJ=∠FCO,∠CEJ=∠COF=90°,
∴△CEJ∽△COF,
∴==,
∴==,
∴EJ=,
∵BF=CJ,∠H=∠CEJ,∠CJE=∠BFH,
∴△BHF≌△CEJ(AAS),
∴FH=EJ=,
∵AE∥BH,
∴=,
∴=,
整理得,10x2+7xy﹣6y2=0,
解得x=y或x=﹣y(舍弃),
∴y=2x,
∴=,
解得x=或﹣(舍弃).
∴BF=,
故选:A.
6.【解答】解:∵半径OC⊥弦AB于点D,
∴=,AD=BD,
∴∠E=∠BOC=22.5°,
∴∠BOD=45°,
∴△ODB是等腰直角三角形,
∵AB=8,
∴DB=OD=4,
则半径OB等于:=4.
故选:B.
7.【解答】解:∵⊙O的半径OA长1,若OB=,
∴OA<OB,
∴点B在圆外,
故选:D.
8.【解答】解:∵∠CDB=30°,
∴∠COB=2∠CDB=60°,
∵CD⊥AB,⊙O的半径为6cm,
∴CE=DE,∠OCE=90°﹣60°=30°,OC=6cm,
∴OE=OC=3cm,CE=OE=3cm,
∴CD=2CE=6cm;
故选:D.
9.【解答】解延长AD交⊙O于C,连接BC,如图,
∵OD⊥AC,
∴AD=CD,
在Rt△OAD中,AD==4,
∴CD=4,
∵AB为直径,
∴∠ACB=90°,
在Rt△ABC中,BC==6,
在Rt△BCD中,BD==2.
故选:C.
10.【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
二.填空题
11.【解答】解:∵AB为⊙O的直径,
∴∠ADB=90°,
∵AB=AC,
∴AC=5,
在Rt△ADC中,∵AC=5,AD=3,
∴CD==4,
∵×DE×AC=×AD×CD,
∴DE==.
故答案为
12.【解答】解:∵弦AB把圆周分成1:9两部分,
∴弦AB所对圆心角的度数=×360°=36°.
故答案为36°.
13.【解答】解:∵A是⊙O上一点,BC是直径,
∴∠BAC=∠BDC=90°,
在Rt△ABC中,AC=2,AB=4,
由勾股定理得:AB2+AC2=BC2,即BC2=22+42=20,
∵点D在⊙O上且平分,
∴BD=DC,
∴在Rt△BDC中,由勾股定理得:BD2+DC2=BC2,即2DC2=BC2=20,
解得:DC=,
故答案为:.
14.【解答】解:连接OA,如图,
∵OC⊥AB,
∴AD=BD,
∵OD=DC,
∴OD=OA=,
∴AD==,AB=2AD=.
当点P为AB所对的优弧的中点时,△APB的面积最大,此时PD=PO+OD=1+=.
∴△APB的面积的最大值为==.
故答案为:.
15.【解答】解:连结OA、OB,作△ABC的外接圆D,如图1,
∵OA=OB=2,AB=2,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠APB=∠AOB=30°,
∵AC⊥AP,
∴∠C=60°,
∵AB=2,要使△ABC的最大面积,则点C到AB的距离最大,
∵∠ACB=60°,点C在⊙D上,
∴∠ADB=120°,如图2,
当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为AB2=,
∴△ABC的最大面积为.
故答案为:.
三.解答题
16.【解答】解:连接OC,如图,
∵CD⊥AB,
∴CE=DE,
∵EB=9,AE=1,
∴AB=10,OC=OA=5,
∴OE=4,
在Rt△OCE中,CE==3,
∴CD=2CE=6.
17.【解答】证明:(1)∵AB=CD,
∴=,
即+=+,
∴=,
∴AC=BD;
(2)∵=,
∴∠ADC=∠DAB,
∴EA=ED,
∵AB=CD,
即AE+BE=CE+DE,
∴CE=BE.
18.【解答】解:(1)∵=,
∴∠ABC=∠ACB=80°,
∴∠A=180°﹣80°﹣80°=20°,
∴∠BOC=2∠A=40°;
(2)作OH⊥BC于H,如图,则BH=CH=BC=5,
在Rt△OBH中,OH===12,
即点O到BC的距离为12.
19.【解答】解:(1)作OH⊥MN于H,连接ON,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,OP=2,
在Rt△POH中,∵∠OPH=45°,
∴OH=OP=,
在Rt△OHN中,∵ON=4,OH=,
∴NH===,
∵OH⊥MN,
∴HM=HN,
∴MN=2NH=2;
(2)作OH⊥MN于H,连接ON,
则HM=HN,
∵MP=3,NP=5,
∴MN=8,
∴HM=HN=4,
∴PH=1,
在Rt△POH中,∵∠OPH=45°,
∴OH=1,
在Rt△OHN中,∵HN=4,OH=1,
∴ON==,
∴AB=2ON=2;
(3)的值不发生变化,为定值,
作OH⊥MN于H,连接ON,
则HM=HN,
设圆的半径为R,
在Rt△OHN中,OH2+NH2=ON2=R2,
在Rt△POH中,∵∠OPH=45°,
∴OH=PH,
∴PH2+NH2=R2,
∵PM2+PN2=(HM﹣PH)2+(NH+PH)2
=(NH﹣PH)2+(NH+PH)2
=2(PH2+NH2)
=2R2.
又AB2=4R2,
∴==
∴的值不发生变化,为定值
一.选择题
1.如图,A,B,C三点在⊙O上,若∠ACB=120°,则∠AOB的度数是( )
A.60° B.90° C.100° D.120°
2.如图,AB是⊙O的直径,若∠BAC=20°,则∠ADC=( )
A.40° B.60° C.70° D.80°
3.如图,圆的两条弦AB,CD相交于点E,且,∠A=35°,则且∠CEB的度数为( )
A.50° B.80° C.70° D.90°
4.下面说法正确的是( )
A.一条路已经修了80%千米
B.半径是2厘米的圆,它的周长和面积相等
C.某班的出勤率达到101%
D.某校的男同学人数比女同学人数多10%
5.如图,点C是半圆O的中点,AB是直径,CF⊥弦AD于点E,交AB于点F,若CE=1,EF=,则BF的长为( )
A. B.1 C. D.
6.如图,⊙O中,半径OC⊥弦AB于点D,点E在⊙O上,∠E=22.5°,AB=8,则半径OB等于( )
A. B. C.4 D.5
7.已知⊙O的半径OA长为1,OB=,则可以得到的正确图形可能是( )
A. B.
C. D.
8.如图,AB是⊙O的直径,弦CD⊥AB于点E.∠CDB=30°,⊙O的半径为6cm.则弦CD的长为( )
A.3cm B.6cm C.3cm D.6cm
9.如图,AB是⊙O的直径,点D为⊙O内一点,连接OD、AD、BD,且AD⊥OD,垂足为D,若AB=10,OD=3,则BD的长为( )
A.2 B.4 C.2 D.4.8
10.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
二.填空题
11.如图,已知AB为⊙O的直径,AB=AC,⊙O交BC于D,DE⊥AC于E,⊙O的半径为2.5,AD=3,则DE的长为 .
12.已知弦AB把圆周分成1:9两部分,则弦AB所对圆心角的度数为 .
13.如图,A是⊙O上一点,BC是直径,AC=2,AB=4,点D在⊙O上且平分,则DC的长为 .
14.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D,且OD=DC,P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则S△PAB的最大值为 .
15.如图,⊙O的半径为2.弦AB=2,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是 .
三.解答题
16.如图AB是⊙O的直径,弦CD⊥AB于点E,若EB=9,AE=1,求弦CD的长.
17.如图,⊙O中的弦AB=CD,AB与CD相交于点E.求证:
(1)AC=BD;
(2)CE=BE.
18.如图,在⊙O中.
(1)若=,∠ACB=80°,求∠BOC的度数;
(2)若⊙O的半径为13,且BC=10,求点O到BC的距离.
19.如图,在⊙O中,AB是直径,P为AB上一点,过点P作弦MN,∠NPB=45°.
(1)若AP=2,BP=6,求MN的长;
(2)若MP=3,NP=5,求AB的长;
(3)当P在AB上运动时(∠NPB=45°不变),的值是否发生变化?若不变,请求出其值;若变化,请求出其范围.
参考答案与试题解析
一.选择题
1.【解答】解:如图,在优弧AB上取一点D,连接AD,BD.
∵∠ACB+∠ADB=180°,∠ACB=120°,
∴∠ADB=60°,
∴∠AOB=2∠ADB=120°,
故选:D.
2.【解答】解:∵AB是直径,
∴∠ACB=90°,
∵∠BAC=20°,
∴∠ABC=90°﹣20°=70°,
∴∠ADC=∠ABC=70°,
故选:C.
3.【解答】解:∴=,
∴∠C=∠A=35°,
∴∠CEB=∠A+∠C=35°+35°=70°.
故选:C.
4.【解答】解:A:根据百分数意义,百分数表示一个数是另一个数的百分之几,不能表示具体数量,无单位,故错误;
B:圆的周长单位是厘米,面积单位是平方厘米,两者之间无法比较大小,故错误;
C:出勤率最高为100%,不可能更大了,因此选项错误;
故选:D.
5.【解答】解:如图,连接AC,BC,OC,过点B作BH⊥CF交CF的延长线于H,设OC交AD于J.
∵=,
∴AC=BC,OC⊥AB,
∵AB是直径,
∴ACB=90°,
∴∠ACJ=∠CBF=45°,
∵CF⊥AD,
∴∠ACF+∠CAJ=90°,∠ACF+∠BCF=90°,
∴∠CAJ=∠BCF,
∴△CAJ≌△BCF(ASA),
∴CJ=BF,AJ=CF=1+=,
∵OC=OB,
∴OJ=OF,设BF=CJ=x.OJ=OF=y,
∵∠AEC=∠H=90°,∠CAE=∠BCH,CA=CB,
∴△ACE≌△CBH(AAS),
∴EC=BH=1,
∵∠ECJ=∠FCO,∠CEJ=∠COF=90°,
∴△CEJ∽△COF,
∴==,
∴==,
∴EJ=,
∵BF=CJ,∠H=∠CEJ,∠CJE=∠BFH,
∴△BHF≌△CEJ(AAS),
∴FH=EJ=,
∵AE∥BH,
∴=,
∴=,
整理得,10x2+7xy﹣6y2=0,
解得x=y或x=﹣y(舍弃),
∴y=2x,
∴=,
解得x=或﹣(舍弃).
∴BF=,
故选:A.
6.【解答】解:∵半径OC⊥弦AB于点D,
∴=,AD=BD,
∴∠E=∠BOC=22.5°,
∴∠BOD=45°,
∴△ODB是等腰直角三角形,
∵AB=8,
∴DB=OD=4,
则半径OB等于:=4.
故选:B.
7.【解答】解:∵⊙O的半径OA长1,若OB=,
∴OA<OB,
∴点B在圆外,
故选:D.
8.【解答】解:∵∠CDB=30°,
∴∠COB=2∠CDB=60°,
∵CD⊥AB,⊙O的半径为6cm,
∴CE=DE,∠OCE=90°﹣60°=30°,OC=6cm,
∴OE=OC=3cm,CE=OE=3cm,
∴CD=2CE=6cm;
故选:D.
9.【解答】解延长AD交⊙O于C,连接BC,如图,
∵OD⊥AC,
∴AD=CD,
在Rt△OAD中,AD==4,
∴CD=4,
∵AB为直径,
∴∠ACB=90°,
在Rt△ABC中,BC==6,
在Rt△BCD中,BD==2.
故选:C.
10.【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
二.填空题
11.【解答】解:∵AB为⊙O的直径,
∴∠ADB=90°,
∵AB=AC,
∴AC=5,
在Rt△ADC中,∵AC=5,AD=3,
∴CD==4,
∵×DE×AC=×AD×CD,
∴DE==.
故答案为
12.【解答】解:∵弦AB把圆周分成1:9两部分,
∴弦AB所对圆心角的度数=×360°=36°.
故答案为36°.
13.【解答】解:∵A是⊙O上一点,BC是直径,
∴∠BAC=∠BDC=90°,
在Rt△ABC中,AC=2,AB=4,
由勾股定理得:AB2+AC2=BC2,即BC2=22+42=20,
∵点D在⊙O上且平分,
∴BD=DC,
∴在Rt△BDC中,由勾股定理得:BD2+DC2=BC2,即2DC2=BC2=20,
解得:DC=,
故答案为:.
14.【解答】解:连接OA,如图,
∵OC⊥AB,
∴AD=BD,
∵OD=DC,
∴OD=OA=,
∴AD==,AB=2AD=.
当点P为AB所对的优弧的中点时,△APB的面积最大,此时PD=PO+OD=1+=.
∴△APB的面积的最大值为==.
故答案为:.
15.【解答】解:连结OA、OB,作△ABC的外接圆D,如图1,
∵OA=OB=2,AB=2,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠APB=∠AOB=30°,
∵AC⊥AP,
∴∠C=60°,
∵AB=2,要使△ABC的最大面积,则点C到AB的距离最大,
∵∠ACB=60°,点C在⊙D上,
∴∠ADB=120°,如图2,
当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为AB2=,
∴△ABC的最大面积为.
故答案为:.
三.解答题
16.【解答】解:连接OC,如图,
∵CD⊥AB,
∴CE=DE,
∵EB=9,AE=1,
∴AB=10,OC=OA=5,
∴OE=4,
在Rt△OCE中,CE==3,
∴CD=2CE=6.
17.【解答】证明:(1)∵AB=CD,
∴=,
即+=+,
∴=,
∴AC=BD;
(2)∵=,
∴∠ADC=∠DAB,
∴EA=ED,
∵AB=CD,
即AE+BE=CE+DE,
∴CE=BE.
18.【解答】解:(1)∵=,
∴∠ABC=∠ACB=80°,
∴∠A=180°﹣80°﹣80°=20°,
∴∠BOC=2∠A=40°;
(2)作OH⊥BC于H,如图,则BH=CH=BC=5,
在Rt△OBH中,OH===12,
即点O到BC的距离为12.
19.【解答】解:(1)作OH⊥MN于H,连接ON,
∵AP=2,BP=6,
∴AB=8,
∴OA=4,OP=2,
在Rt△POH中,∵∠OPH=45°,
∴OH=OP=,
在Rt△OHN中,∵ON=4,OH=,
∴NH===,
∵OH⊥MN,
∴HM=HN,
∴MN=2NH=2;
(2)作OH⊥MN于H,连接ON,
则HM=HN,
∵MP=3,NP=5,
∴MN=8,
∴HM=HN=4,
∴PH=1,
在Rt△POH中,∵∠OPH=45°,
∴OH=1,
在Rt△OHN中,∵HN=4,OH=1,
∴ON==,
∴AB=2ON=2;
(3)的值不发生变化,为定值,
作OH⊥MN于H,连接ON,
则HM=HN,
设圆的半径为R,
在Rt△OHN中,OH2+NH2=ON2=R2,
在Rt△POH中,∵∠OPH=45°,
∴OH=PH,
∴PH2+NH2=R2,
∵PM2+PN2=(HM﹣PH)2+(NH+PH)2
=(NH﹣PH)2+(NH+PH)2
=2(PH2+NH2)
=2R2.
又AB2=4R2,
∴==
∴的值不发生变化,为定值
同课章节目录
