人教版八年级数学上册一课一练13.4 课题学习 最短路径问题(word版,含答案解析)
文档属性
| 名称 | 人教版八年级数学上册一课一练13.4 课题学习 最短路径问题(word版,含答案解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 19:08:56 | ||
图片预览




文档简介
人教版八年级数学上册13.4
课题学习
最短路径问题
一、选择题(共16小题;共80分)
1.
如图,直线
是一条河,,
两地相距
千米,,
两地到
的距离分别为
千米,
千米,欲在
上的某点
处修建一个水泵站,向
,
两地供水,现有如图所示的四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是
A.
B.
C.
D.
2.
如图,在等边三角形
中,
边上的高
,
是高
上的一个动点,
是边
的中点,在点
运动的过程中,存在
的最小值,则这个最小值是
A.
B.
C.
D.
3.
如图,把一副常用的三角板如图所示拼在一起,那么图中
的度数为
A.
B.
C.
D.
4.
如图所示,等边
的边长为
,
是
的平分线
上一点,
是
边上的一个动点,则
的最小值为
A.
B.
C.
D.
5.
直线
是一条河,,
是两个村庄,欲在
上的某处修建一个水泵站,向
,
两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是
A.
B.
C.
D.
6.
如图,直线
表示一条河,点
、
表示两个村庄,计划在
上的某处修建一个水泵向两个村庄供水.在下面四种铺设管道的方案中,所需管道最短的方案是
(图中实线表示铺设的管道)
A.
B.
C.
D.
7.
如图,,,
分别是边
,
上的定点,,
分别是边
,
上的动点,记
,,当
最小时,则关于
,
的数量关系正确的是
A.
B.
C.
D.
8.
如图,四边形
中,,,,
分别是
,
上的点,当
的周长最小时,
的度数为
A.
B.
C.
D.
9.
如图,点
是
内任意一点,且
,点
和点
分别是射线
和射线
上的动点,当
周长取最小值时,则
的度数为
A.
B.
C.
D.
10.
如图,,
内有一定点
,且
,在
上有一动点
,
上有一动点
.若
周长最小,则最小周长是
A.
B.
C.
D.
11.
如图,,点
是
内任意一点,,点
和点
分别是射线
和射线
上的动点,若
周长的最小值是
,则
的值是
A.
B.
C.
D.
12.
如图,已知直线
,且
与
之间的距离为
,点
到直线
的距离为
,点
到直线
的距离为
,.试在直线
上找一点
,在直线
上找一点
,满足
且
的长度最短,则此时
A.
B.
C.
D.
13.
如图,在
中,,,,
为
上一点,且
,
平分
交
于
.若
是
上的动点,则
的最小值等于
A.
B.
C.
D.
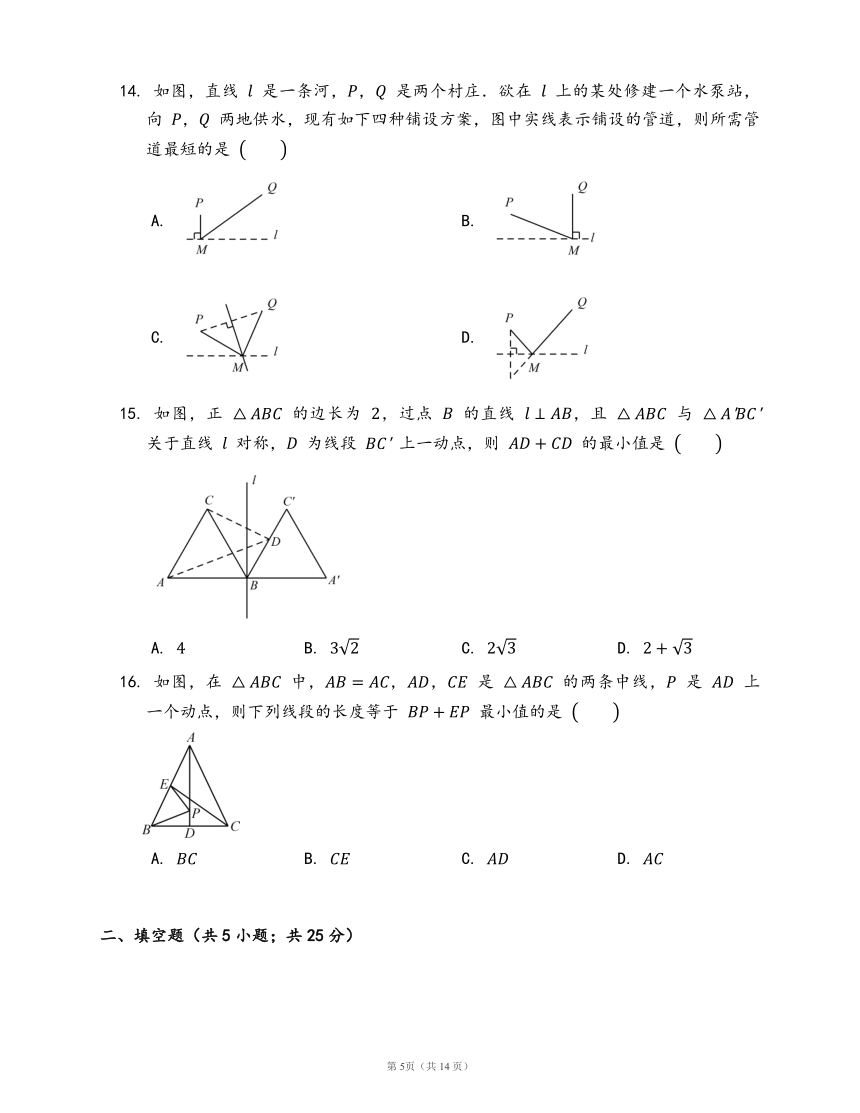
14.
如图,直线
是一条河,,
是两个村庄.欲在
上的某处修建一个水泵站,向
,
两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是
A.
B.
C.
D.
15.
如图,正
的边长为
,过点
的直线
,且
与
关于直线
对称,
为线段
上一动点,则
的最小值是
A.
B.
C.
D.
16.
如图,在
中,,,
是
的两条中线,
是
上一个动点,则下列线段的长度等于
最小值的是
A.
B.
C.
D.
二、填空题(共5小题;共25分)
17.
如图,等边
的边长为
,
是
边上的中线,
是
边上的动点,
是
边上一点.若
,当
取得最小值时,则
的度数为
?.
18.
如图:点
为
内一点,分别作出
点关于
、
的对称点
,,连接
交
于
,交
于
,,则
的周长为
?.
19.
如图,在
中,
边上的垂直平分线
交边
于点
,交边
于点
.若
的周长为
,
与四边形
的周长之差为
,则线段
的长为
?.
20.
如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个"半圆柱"而成,中间可供滑行的部分的截面是半径为
的半圆,其边缘
,小明要在
上选取一点
,能够使他从点
滑到点
再到点
的滑行距离最短,则他滑行的最短距离为
?
.(
取
)
21.
在平面直角坐标系
中,点
,,当点
在第一象限,且坐标为
?
时,
为等腰直角三角形.
三、解答题(共3小题;共45分)
22.
用圆规、直尺作图,不写作法,但要保留作图痕迹.
如图所示,某汽车探险队要从
城穿越沙漠到
城,途中需要到河流
边为汽车加水,则汽车在河边哪一点加水,才能使行驶的总路程最短?请你在图上画出这一点.
23.
如图,在旷野上,一个人骑着马从
到
,半路上他必须先到河岸
的
点去让马饮水,然后在让马到河岸
的
点再次饮水,最后到达
点,他应该如何选择饮马地点
、
,才能使所走的路程的
为最短?(
假定河岸
、
是直线)
24.
如图,已知平面直角坐标系中,,
两点的坐标分别为
,.
(1)若
是
轴上的一个动点,则当
?
时,
的周长最短.
(2)若
,
是
轴上的两个动点,则当
?
时,四边形
的周长最短.
(3)设
,
分别为
轴和
轴上的动点,请问:是否存在这样的点
,,使四边形
的周长最短?若存在,请写出
和
的值;若不存在,请说明理由.
答案
第一部分
1.
B
2.
B
【解析】连接
,
等边
中,
是
边上的高线,即
垂直平分
,
,
当
,,
三点共线时,,
等边
中,
是
边的中点,
,
的最小值为
.
3.
D
4.
B
5.
D
6.
D
7.
D
8.
D
【解析】作
关于
和
的对称点
,,连接
,交
于
,交
于
,则
即为
的周长最小值.作
延长线
.
,
.
.
.
,,
.
.
9.
B
【解析】分别作点
关于
,
的对称点
,,连接
,分别交
,
于点
,,如图所示:
此时
的周长取最小值.
,
,
,
,,
,
,
.
10.
B
【解析】设
,则
,作
与
相交于
,并将
延长一倍到
,即
,
作
与
相交于
,并将
延长一倍到
,即
,
连接
与
相交于
,与
相交于
,再连接
,,连接
,,则
即为周长最短的三角形,
是
的垂直平分线,
;
同理,
是
的垂直平分线,
,
的周长
,
,且
,
是等边三角形,
,即在保持
的条件下
的最小周长为
.
11.
B
12.
B
13.
D
【解析】如图,作点
关于
的对称点
,连接
交
于
,连接
,此时
的值最小,作
于
.
,,,
,
,
,
,
,
,
故选:D.
14.
D
15.
A
【解析】如图所示.
过点
作
的对称点
,连接
,与
的延长线交于点
.
此时,
为最小值
.
点
在线段
上,
点
在点
处.
的最小值为
.
16.
B
【解析】如图连接
,
,,
,
,
,
,
,,
共线时,
的值最小,最小值为
的长度.
第二部分
17.
【解析】如图,
取
的中点
,连接
交
于点
,
因为等边
的边长为
,,
所以点
是
的中点,
所以点
和点
关于
对称,
此时
最小,
根据等边三角形的性质可知:.
所以
的度数为
.
18.
19.
20.
【解析】其侧面展开图如图:作点
关于
的对称点
,连接
.
中间可供滑行的部分的截面是半径为
的半圆,
.
.
在
中,.
21.
,,
第三部分
22.
如下图所示,本题可以进行数学建模,即在直线
上作一点
,使它到同侧点
,
的距离之和最小.
作法:作点
关于直线
的对称点
,连接
,则
与直线
的交点
即为所求的点.
23.
如图,分别作
点关于直线
的对称点
、
点关于直线
的对称点
,连接
,分别交
于点
,交
于点
,连接
、
,所以路程
最短.
24.
(1)
如图点
即为所求.
.
【解析】直线
的解析式为
.
??????(2)
如图点
即为所求.
.
【解析】直线
的解析式为
.
??????(3)
如图点
,
即为所求.
,.
【解析】直线
的解析式为
.
第5页(共15
页)
课题学习
最短路径问题
一、选择题(共16小题;共80分)
1.
如图,直线
是一条河,,
两地相距
千米,,
两地到
的距离分别为
千米,
千米,欲在
上的某点
处修建一个水泵站,向
,
两地供水,现有如图所示的四种铺设方案,图中实线表示铺设的管道,则铺设的管道最短的是
A.
B.
C.
D.
2.
如图,在等边三角形
中,
边上的高
,
是高
上的一个动点,
是边
的中点,在点
运动的过程中,存在
的最小值,则这个最小值是
A.
B.
C.
D.
3.
如图,把一副常用的三角板如图所示拼在一起,那么图中
的度数为
A.
B.
C.
D.
4.
如图所示,等边
的边长为
,
是
的平分线
上一点,
是
边上的一个动点,则
的最小值为
A.
B.
C.
D.
5.
直线
是一条河,,
是两个村庄,欲在
上的某处修建一个水泵站,向
,
两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是
A.
B.
C.
D.
6.
如图,直线
表示一条河,点
、
表示两个村庄,计划在
上的某处修建一个水泵向两个村庄供水.在下面四种铺设管道的方案中,所需管道最短的方案是
(图中实线表示铺设的管道)
A.
B.
C.
D.
7.
如图,,,
分别是边
,
上的定点,,
分别是边
,
上的动点,记
,,当
最小时,则关于
,
的数量关系正确的是
A.
B.
C.
D.
8.
如图,四边形
中,,,,
分别是
,
上的点,当
的周长最小时,
的度数为
A.
B.
C.
D.
9.
如图,点
是
内任意一点,且
,点
和点
分别是射线
和射线
上的动点,当
周长取最小值时,则
的度数为
A.
B.
C.
D.
10.
如图,,
内有一定点
,且
,在
上有一动点
,
上有一动点
.若
周长最小,则最小周长是
A.
B.
C.
D.
11.
如图,,点
是
内任意一点,,点
和点
分别是射线
和射线
上的动点,若
周长的最小值是
,则
的值是
A.
B.
C.
D.
12.
如图,已知直线
,且
与
之间的距离为
,点
到直线
的距离为
,点
到直线
的距离为
,.试在直线
上找一点
,在直线
上找一点
,满足
且
的长度最短,则此时
A.
B.
C.
D.
13.
如图,在
中,,,,
为
上一点,且
,
平分
交
于
.若
是
上的动点,则
的最小值等于
A.
B.
C.
D.
14.
如图,直线
是一条河,,
是两个村庄.欲在
上的某处修建一个水泵站,向
,
两地供水,现有如下四种铺设方案,图中实线表示铺设的管道,则所需管道最短的是
A.
B.
C.
D.
15.
如图,正
的边长为
,过点
的直线
,且
与
关于直线
对称,
为线段
上一动点,则
的最小值是
A.
B.
C.
D.
16.
如图,在
中,,,
是
的两条中线,
是
上一个动点,则下列线段的长度等于
最小值的是
A.
B.
C.
D.
二、填空题(共5小题;共25分)
17.
如图,等边
的边长为
,
是
边上的中线,
是
边上的动点,
是
边上一点.若
,当
取得最小值时,则
的度数为
?.
18.
如图:点
为
内一点,分别作出
点关于
、
的对称点
,,连接
交
于
,交
于
,,则
的周长为
?.
19.
如图,在
中,
边上的垂直平分线
交边
于点
,交边
于点
.若
的周长为
,
与四边形
的周长之差为
,则线段
的长为
?.
20.
如图,是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个"半圆柱"而成,中间可供滑行的部分的截面是半径为
的半圆,其边缘
,小明要在
上选取一点
,能够使他从点
滑到点
再到点
的滑行距离最短,则他滑行的最短距离为
?
.(
取
)
21.
在平面直角坐标系
中,点
,,当点
在第一象限,且坐标为
?
时,
为等腰直角三角形.
三、解答题(共3小题;共45分)
22.
用圆规、直尺作图,不写作法,但要保留作图痕迹.
如图所示,某汽车探险队要从
城穿越沙漠到
城,途中需要到河流
边为汽车加水,则汽车在河边哪一点加水,才能使行驶的总路程最短?请你在图上画出这一点.
23.
如图,在旷野上,一个人骑着马从
到
,半路上他必须先到河岸
的
点去让马饮水,然后在让马到河岸
的
点再次饮水,最后到达
点,他应该如何选择饮马地点
、
,才能使所走的路程的
为最短?(
假定河岸
、
是直线)
24.
如图,已知平面直角坐标系中,,
两点的坐标分别为
,.
(1)若
是
轴上的一个动点,则当
?
时,
的周长最短.
(2)若
,
是
轴上的两个动点,则当
?
时,四边形
的周长最短.
(3)设
,
分别为
轴和
轴上的动点,请问:是否存在这样的点
,,使四边形
的周长最短?若存在,请写出
和
的值;若不存在,请说明理由.
答案
第一部分
1.
B
2.
B
【解析】连接
,
等边
中,
是
边上的高线,即
垂直平分
,
,
当
,,
三点共线时,,
等边
中,
是
边的中点,
,
的最小值为
.
3.
D
4.
B
5.
D
6.
D
7.
D
8.
D
【解析】作
关于
和
的对称点
,,连接
,交
于
,交
于
,则
即为
的周长最小值.作
延长线
.
,
.
.
.
,,
.
.
9.
B
【解析】分别作点
关于
,
的对称点
,,连接
,分别交
,
于点
,,如图所示:
此时
的周长取最小值.
,
,
,
,,
,
,
.
10.
B
【解析】设
,则
,作
与
相交于
,并将
延长一倍到
,即
,
作
与
相交于
,并将
延长一倍到
,即
,
连接
与
相交于
,与
相交于
,再连接
,,连接
,,则
即为周长最短的三角形,
是
的垂直平分线,
;
同理,
是
的垂直平分线,
,
的周长
,
,且
,
是等边三角形,
,即在保持
的条件下
的最小周长为
.
11.
B
12.
B
13.
D
【解析】如图,作点
关于
的对称点
,连接
交
于
,连接
,此时
的值最小,作
于
.
,,,
,
,
,
,
,
,
故选:D.
14.
D
15.
A
【解析】如图所示.
过点
作
的对称点
,连接
,与
的延长线交于点
.
此时,
为最小值
.
点
在线段
上,
点
在点
处.
的最小值为
.
16.
B
【解析】如图连接
,
,,
,
,
,
,
,,
共线时,
的值最小,最小值为
的长度.
第二部分
17.
【解析】如图,
取
的中点
,连接
交
于点
,
因为等边
的边长为
,,
所以点
是
的中点,
所以点
和点
关于
对称,
此时
最小,
根据等边三角形的性质可知:.
所以
的度数为
.
18.
19.
20.
【解析】其侧面展开图如图:作点
关于
的对称点
,连接
.
中间可供滑行的部分的截面是半径为
的半圆,
.
.
在
中,.
21.
,,
第三部分
22.
如下图所示,本题可以进行数学建模,即在直线
上作一点
,使它到同侧点
,
的距离之和最小.
作法:作点
关于直线
的对称点
,连接
,则
与直线
的交点
即为所求的点.
23.
如图,分别作
点关于直线
的对称点
、
点关于直线
的对称点
,连接
,分别交
于点
,交
于点
,连接
、
,所以路程
最短.
24.
(1)
如图点
即为所求.
.
【解析】直线
的解析式为
.
??????(2)
如图点
即为所求.
.
【解析】直线
的解析式为
.
??????(3)
如图点
,
即为所求.
,.
【解析】直线
的解析式为
.
第5页(共15
页)
