规律探索中的常用数列
图片预览


文档简介
规 律 探 索 中 的 常 用 数 列
按照某种特征有秩序排列的一些数通常称为数列。在图形的计数、面积的计算、坐标的变换等方面经常用到数列。下面介绍几种中学数学中常用数列及其计算方法。
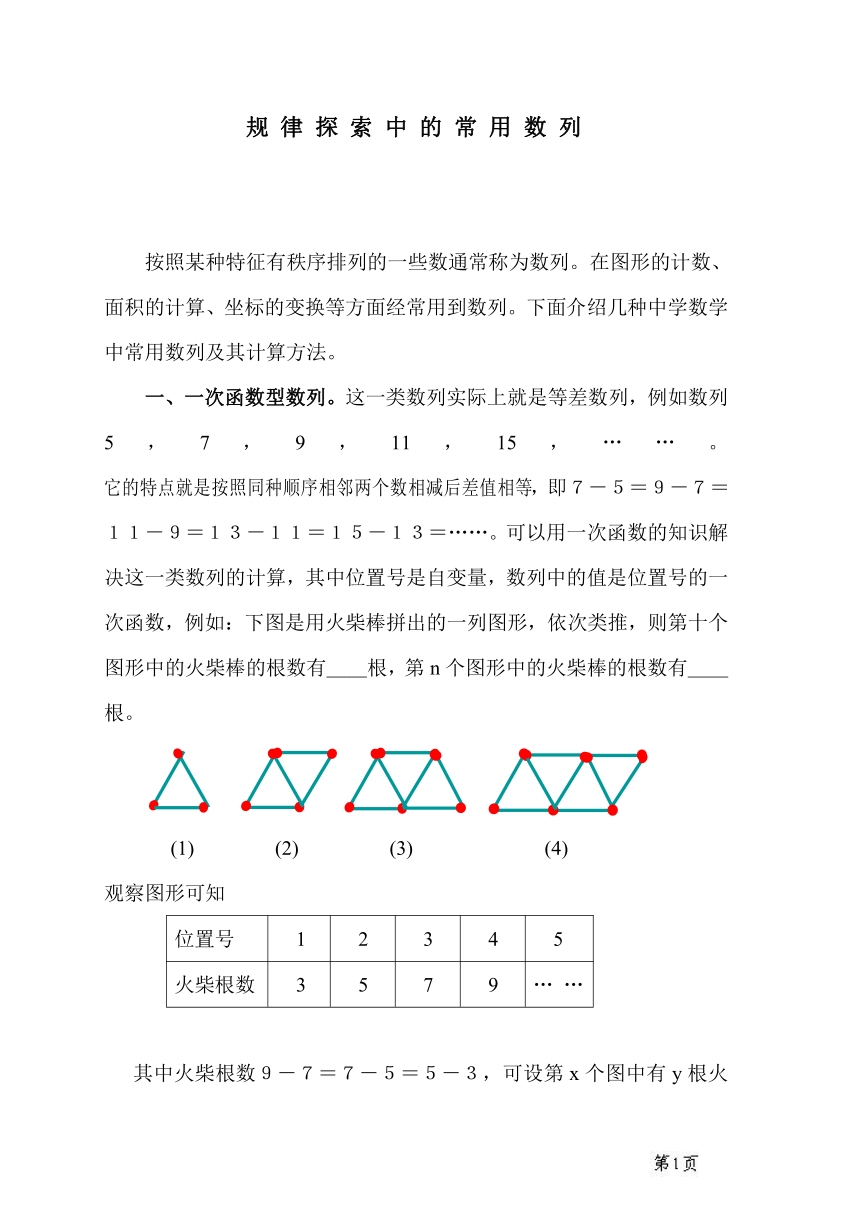
一、一次函数型数列。这一类数列实际上就是等差数列,例如数列5,7,9,11,15,……。它的特点就是按照同种顺序相邻两个数相减后差值相等,即7-5=9-7=11-9=13-11=15-13=……。可以用一次函数的知识解决这一类数列的计算,其中位置号是自变量,数列中的值是位置号的一次函数,例如:下图是用火柴棒拼出的一列图形,依次类推,则第十个图形中的火柴棒的根数有__根,第n个图形中的火柴棒的根数有__根。
(1) (2) (3) (4)
观察图形可知
位置号 1 2 3 4 5
火柴根数 3 5 7 9 … …
其中火柴根数9-7=7-5=5-3,可设第x个图中有y根火柴棒,这时Y是位置号x的一次函数,设y=kx+b,由x=1时y=3, x=2时y=5可得 k+b=3 解方程组得 k=2,b=1,则y=2x+1。第十个
2k+b=5 图形x=10,火柴根数y=2×10=20。第n个图形x=n, 火柴根数y=2n+1。
练一练:1.一根绳子弯成如图形状,当用剪刀沿一条虚线剪断时,绳子被剪成5段;沿两条虚线剪断时,绳子被剪成9段;沿三条虚线剪断时,绳子被剪成13段;以此方法,沿10条虚线剪断时,绳子被剪成多少段?
(1) (2) (3)
二、二次函数型数列。这一类数列的特征是按照同种顺序相邻两数相减后的差值是一组等差数列,也就是按照同种顺序相邻两数相减后的差值再相减所得差值相等。例如:数列1,3,6,10,15,21,28,……。第一次相减:3-1=2,6-1=3,10-6=4,15-10=5,21-15=6,28-21=7, ……。差值再相减:3-2=4-3=5-4=6-5=7-6=……。可以用二次函数的知识解决这一类数列的计算,其中位置号是自变量,数列中的值是位置号的二次函数, 例如:一条直线上一个点可以构成0条线段,两个点可以构成1条线段,三个点可以构成3条线段,四个点可以构成6条线段,以此类推一百个不同的点可以构成多少条线段?
第2页
(1) (2) (3) (4)
观察图形可知由(1)到(4)中线段条数分别有0,1,3,6,……条,相邻两数的差1-0,3-1,6-3,……。是一组等差数列,即0,1,3,6,第一次相减差值为1,2,3,第二次相减差值为1,1(可以简述为数值差的差相等),可设第x个图中有y条线段(即x个不同的点可以构成y条线段),则y是x的二次函数,设y=ax2+bx+c,显然x=1时y=0; x=2时y=1; x=3时y=3.代入y=ax2+bx+c 可得 a+b+c=0 解方程组可得 a =
4a+2b+c=1 b = -
9a+3b+c=3 c = 0
所以y = x2 - x, 当x=100时y = ×1002- ×100=4950.
则100个不同的点可以构成4950条线段。
练一练:2.下面是由大小相同的小正方体木块叠放而成的图形,第一个图中有1个木块,第二个图中有6个木块,第三个图中有15个木块,第四个图中有28个木块,按照这样的规律摆放下去,则第七个图中小木块的个数是多少?
(1) (2) (3) (4) 第3页
三、指数函数型数列。形如y=abx+c(其中a、b、c是常量,指数x是自变量)的函数称为指数函数。这一类数列的特征是按照同种顺序相邻两数的比值相等(也就是等比数列),或者按照同种顺序相邻两数的差值的比值相等(也就是它们的差是等比数列)。例如:数列1,2,4,8,16,32,……。或者数列3,5,9,17,33,65,……。可以用指数函数的知识解决这一类问题的有关计算。可以把位置号当成自变量,数列中的数值是它的位置号的指数函数。例如:将一条长方形的纸条对折一次可以得到1条折痕,保持折痕平行时对折两次可以得到3条折痕,对折三次可以得到7条折痕,对折四次可以得到15条折痕,则对折十次可以得到多少条折痕?
(1) (2) (3) (4)
观察图形可知
位置号 (1) (2) (3) (4) ……
折痕条数 1 3 7 15 ……
折痕条数1,3,7,15,相邻两数相减3-1,7-3,15-7,差值2,4,8是等比数列( = ),可以设第x个图中(对折x次)有y条折痕,y是x的指数函数,令y=abx+c,因为x=1时y=1; x=2时y=3; x=3时y=7,所以可得方程组 1=ab+c 消去c可得
3=ab2+c
7=ab3+c
第4页
2=ab2-ab (1)
6=ab3-ab (2), (2)÷(1)消去a得(b2-1)÷(b-1)=3因为b≠1,所以b+1=3,得出b=2,则a=1,c=-1.由此得出y=2x-1,对折十次时x=10,折痕数y=210-1=1023条。
练一练:3.下面是按规律排成的一列数,从左向右数第九个数是多少?
3,5,9,17,33,65,……
函数是反映现实生活中变量之间的变化关系的一种数学模型,而数列通常是按照某种规律随位置变化的一些数值,它本身就是一种函数关系,所以很多数列都能用函数知识加以解决,只要大家在学习中细心观察,认真总结,许多数列问题都能迎刃而解。
练一练答案:1. 沿10条虚线剪断时,绳子被剪成10×4+1=41条。
2. 第七个图中小木块的个数是120个。
3. 第九个数是29+1=513.
第5页
按照某种特征有秩序排列的一些数通常称为数列。在图形的计数、面积的计算、坐标的变换等方面经常用到数列。下面介绍几种中学数学中常用数列及其计算方法。
一、一次函数型数列。这一类数列实际上就是等差数列,例如数列5,7,9,11,15,……。它的特点就是按照同种顺序相邻两个数相减后差值相等,即7-5=9-7=11-9=13-11=15-13=……。可以用一次函数的知识解决这一类数列的计算,其中位置号是自变量,数列中的值是位置号的一次函数,例如:下图是用火柴棒拼出的一列图形,依次类推,则第十个图形中的火柴棒的根数有__根,第n个图形中的火柴棒的根数有__根。
(1) (2) (3) (4)
观察图形可知
位置号 1 2 3 4 5
火柴根数 3 5 7 9 … …
其中火柴根数9-7=7-5=5-3,可设第x个图中有y根火柴棒,这时Y是位置号x的一次函数,设y=kx+b,由x=1时y=3, x=2时y=5可得 k+b=3 解方程组得 k=2,b=1,则y=2x+1。第十个
2k+b=5 图形x=10,火柴根数y=2×10=20。第n个图形x=n, 火柴根数y=2n+1。
练一练:1.一根绳子弯成如图形状,当用剪刀沿一条虚线剪断时,绳子被剪成5段;沿两条虚线剪断时,绳子被剪成9段;沿三条虚线剪断时,绳子被剪成13段;以此方法,沿10条虚线剪断时,绳子被剪成多少段?
(1) (2) (3)
二、二次函数型数列。这一类数列的特征是按照同种顺序相邻两数相减后的差值是一组等差数列,也就是按照同种顺序相邻两数相减后的差值再相减所得差值相等。例如:数列1,3,6,10,15,21,28,……。第一次相减:3-1=2,6-1=3,10-6=4,15-10=5,21-15=6,28-21=7, ……。差值再相减:3-2=4-3=5-4=6-5=7-6=……。可以用二次函数的知识解决这一类数列的计算,其中位置号是自变量,数列中的值是位置号的二次函数, 例如:一条直线上一个点可以构成0条线段,两个点可以构成1条线段,三个点可以构成3条线段,四个点可以构成6条线段,以此类推一百个不同的点可以构成多少条线段?
第2页
(1) (2) (3) (4)
观察图形可知由(1)到(4)中线段条数分别有0,1,3,6,……条,相邻两数的差1-0,3-1,6-3,……。是一组等差数列,即0,1,3,6,第一次相减差值为1,2,3,第二次相减差值为1,1(可以简述为数值差的差相等),可设第x个图中有y条线段(即x个不同的点可以构成y条线段),则y是x的二次函数,设y=ax2+bx+c,显然x=1时y=0; x=2时y=1; x=3时y=3.代入y=ax2+bx+c 可得 a+b+c=0 解方程组可得 a =
4a+2b+c=1 b = -
9a+3b+c=3 c = 0
所以y = x2 - x, 当x=100时y = ×1002- ×100=4950.
则100个不同的点可以构成4950条线段。
练一练:2.下面是由大小相同的小正方体木块叠放而成的图形,第一个图中有1个木块,第二个图中有6个木块,第三个图中有15个木块,第四个图中有28个木块,按照这样的规律摆放下去,则第七个图中小木块的个数是多少?
(1) (2) (3) (4) 第3页
三、指数函数型数列。形如y=abx+c(其中a、b、c是常量,指数x是自变量)的函数称为指数函数。这一类数列的特征是按照同种顺序相邻两数的比值相等(也就是等比数列),或者按照同种顺序相邻两数的差值的比值相等(也就是它们的差是等比数列)。例如:数列1,2,4,8,16,32,……。或者数列3,5,9,17,33,65,……。可以用指数函数的知识解决这一类问题的有关计算。可以把位置号当成自变量,数列中的数值是它的位置号的指数函数。例如:将一条长方形的纸条对折一次可以得到1条折痕,保持折痕平行时对折两次可以得到3条折痕,对折三次可以得到7条折痕,对折四次可以得到15条折痕,则对折十次可以得到多少条折痕?
(1) (2) (3) (4)
观察图形可知
位置号 (1) (2) (3) (4) ……
折痕条数 1 3 7 15 ……
折痕条数1,3,7,15,相邻两数相减3-1,7-3,15-7,差值2,4,8是等比数列( = ),可以设第x个图中(对折x次)有y条折痕,y是x的指数函数,令y=abx+c,因为x=1时y=1; x=2时y=3; x=3时y=7,所以可得方程组 1=ab+c 消去c可得
3=ab2+c
7=ab3+c
第4页
2=ab2-ab (1)
6=ab3-ab (2), (2)÷(1)消去a得(b2-1)÷(b-1)=3因为b≠1,所以b+1=3,得出b=2,则a=1,c=-1.由此得出y=2x-1,对折十次时x=10,折痕数y=210-1=1023条。
练一练:3.下面是按规律排成的一列数,从左向右数第九个数是多少?
3,5,9,17,33,65,……
函数是反映现实生活中变量之间的变化关系的一种数学模型,而数列通常是按照某种规律随位置变化的一些数值,它本身就是一种函数关系,所以很多数列都能用函数知识加以解决,只要大家在学习中细心观察,认真总结,许多数列问题都能迎刃而解。
练一练答案:1. 沿10条虚线剪断时,绳子被剪成10×4+1=41条。
2. 第七个图中小木块的个数是120个。
3. 第九个数是29+1=513.
第5页
同课章节目录
