22.1比例线段 第3课时 比例的性质、黄金分割 课件(共26张PPT)
文档属性
| 名称 | 22.1比例线段 第3课时 比例的性质、黄金分割 课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 20:18:58 | ||
图片预览







文档简介
(共26张PPT)
第3课时
比例的性质、黄金分割
22.1
比例线段
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
1.理解比例的基本性质.
2.能根据比例的基本性质求比值.
3.知道黄金分割的定义,会判断某一点是否为一条线段的黄金分割点.
【过程与方法】
经历探索成比例线段的过程,并利用其解决一些简单的问题.
【情感态度】
感知知识的实际应用,增强对知识就是力量的客观认识,进一步加强理论联系实际的学习方法.
【教学重点】
比例的基本性质.
【教学难点】
比例的基本性质及运用.
新课导入
说一说什么叫做两个数的比?比的基本性质是什么?
两个数相除又叫做两个数的比,表示两个比相等的式子叫做比例。
比的基本性质:比的前项和后项都乘或者都除以相同的数(零除外),比值不变。
新课探究
两条线段的比是它们长度的比,也就是两个数的比,因此也应具有关于两个数成比例的性质.
(1)基本性质
如果
,那么
ad=bc(b,d≠0).
反之也成立,即
如果
ad=bc,那么
(b,d≠0).
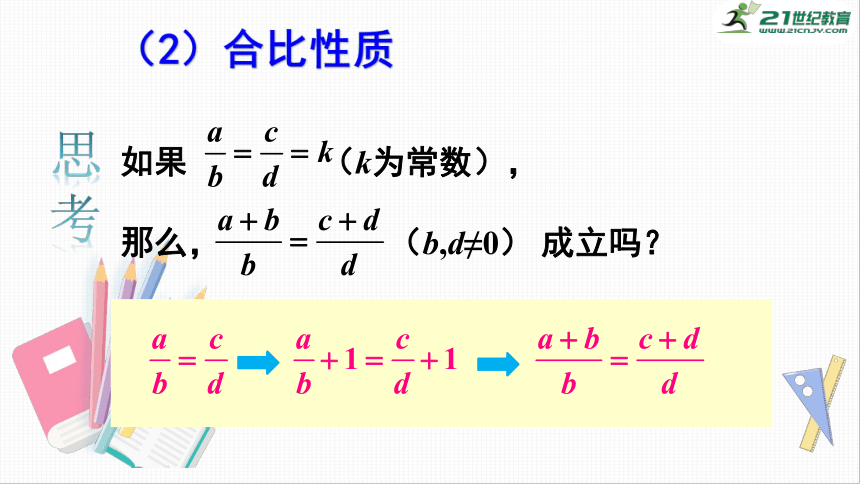
(2)合比性质
思
考
如果
(k为常数),
那么,
(b,d≠0)
成立吗?
(3)等比性质
思
考
如果
,且
,
那么,
成立吗?
b1+b2+···+bn≠0
设
,得
a1=b1k,
a2=b2k,
···,
an=bnk,
代入待证明的等式左边,提取公因式并约分即得等比性质.
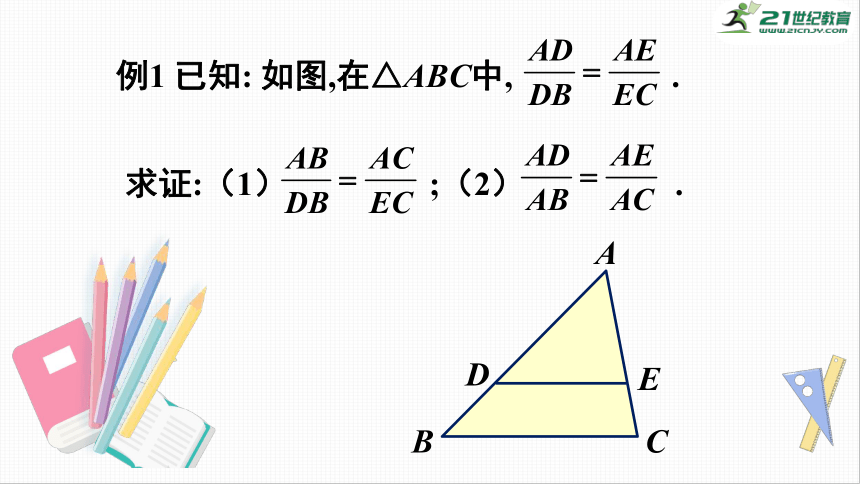
例1
已知:
如图,在△ABC中,
.
求证:(1)
;(2)
.
A
B
C
D
E
A
B
C
D
E
证明(1)∵
,
∴
.
∴
.
(2)∵
,
∴
.
∴
.
∴
.
∴
.
A
B
C
D
E
例2
在地图或工程图纸上,都标有比例尺,比例尺就是图上长度与实际长度的比.现在一张比例尺为
1∶5000
的图纸上,量得一个
△ABC
的三边:AC=3cm,BC=4cm,AB=5cm.问这个图纸所反映的实际
△A′B′C′
的周长是多少?
A
B
C
解
根据题意,得
A
B
C
即
又∵
AB+BC+AC=5+4+3=12(cm
),
∴
A′B′+B′C′+A′C′
=
12×5000=60000(cm)=600(m).
答:实际△A′B′C′的周长是600m.
例3
如图,已知线段
AB
长度为a,点
P
是
AB上一点,且使
AB∶AP
=AP∶PB.求线段
AP
的长和
.
A
P
B
A
P
B
解
设
AP
=
x,那么
PB
=
a-x.
根据题意,得
a∶x
=
x∶(a-x)
,
x2
+
ax
-
a2
=
0.
即
解方程,得
因为线段长度不能是负值,所以取
x
a-x
A
P
B
即
于是
把一条线段分成两部分,使其中较长线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割.
归纳总结
A
P
B
AB∶AP
=AP∶PB
A
P
B
AB∶AP
=AP∶PB
分割点叫做这条线段的黄金分割点.
比值
叫做黄金数.
随堂演练
1.
若
,
则
_____.
2.
如果
,
那么
_____.
9
3.已知三个数
,
请你再添上一个(只填一
个)数,
使它们能构成一个比例式,
则这个数是_________________.
4.已知
,
b+d+f
≠
0,求
的值.
5.
已知点
C
是线段
AB
的黄金分割点,BC
=
AC
+
2,求线段
AC
的长.
A
C
B
解
由题意,得
AB∶BC
=
BC∶AC
∵BC
=
AC
+2,
.
∴
.
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第3课时
比例的性质、黄金分割
22.1
比例线段
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
1.理解比例的基本性质.
2.能根据比例的基本性质求比值.
3.知道黄金分割的定义,会判断某一点是否为一条线段的黄金分割点.
【过程与方法】
经历探索成比例线段的过程,并利用其解决一些简单的问题.
【情感态度】
感知知识的实际应用,增强对知识就是力量的客观认识,进一步加强理论联系实际的学习方法.
【教学重点】
比例的基本性质.
【教学难点】
比例的基本性质及运用.
新课导入
说一说什么叫做两个数的比?比的基本性质是什么?
两个数相除又叫做两个数的比,表示两个比相等的式子叫做比例。
比的基本性质:比的前项和后项都乘或者都除以相同的数(零除外),比值不变。
新课探究
两条线段的比是它们长度的比,也就是两个数的比,因此也应具有关于两个数成比例的性质.
(1)基本性质
如果
,那么
ad=bc(b,d≠0).
反之也成立,即
如果
ad=bc,那么
(b,d≠0).
(2)合比性质
思
考
如果
(k为常数),
那么,
(b,d≠0)
成立吗?
(3)等比性质
思
考
如果
,且
,
那么,
成立吗?
b1+b2+···+bn≠0
设
,得
a1=b1k,
a2=b2k,
···,
an=bnk,
代入待证明的等式左边,提取公因式并约分即得等比性质.
例1
已知:
如图,在△ABC中,
.
求证:(1)
;(2)
.
A
B
C
D
E
A
B
C
D
E
证明(1)∵
,
∴
.
∴
.
(2)∵
,
∴
.
∴
.
∴
.
∴
.
A
B
C
D
E
例2
在地图或工程图纸上,都标有比例尺,比例尺就是图上长度与实际长度的比.现在一张比例尺为
1∶5000
的图纸上,量得一个
△ABC
的三边:AC=3cm,BC=4cm,AB=5cm.问这个图纸所反映的实际
△A′B′C′
的周长是多少?
A
B
C
解
根据题意,得
A
B
C
即
又∵
AB+BC+AC=5+4+3=12(cm
),
∴
A′B′+B′C′+A′C′
=
12×5000=60000(cm)=600(m).
答:实际△A′B′C′的周长是600m.
例3
如图,已知线段
AB
长度为a,点
P
是
AB上一点,且使
AB∶AP
=AP∶PB.求线段
AP
的长和
.
A
P
B
A
P
B
解
设
AP
=
x,那么
PB
=
a-x.
根据题意,得
a∶x
=
x∶(a-x)
,
x2
+
ax
-
a2
=
0.
即
解方程,得
因为线段长度不能是负值,所以取
x
a-x
A
P
B
即
于是
把一条线段分成两部分,使其中较长线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割.
归纳总结
A
P
B
AB∶AP
=AP∶PB
A
P
B
AB∶AP
=AP∶PB
分割点叫做这条线段的黄金分割点.
比值
叫做黄金数.
随堂演练
1.
若
,
则
_____.
2.
如果
,
那么
_____.
9
3.已知三个数
,
请你再添上一个(只填一
个)数,
使它们能构成一个比例式,
则这个数是_________________.
4.已知
,
b+d+f
≠
0,求
的值.
5.
已知点
C
是线段
AB
的黄金分割点,BC
=
AC
+
2,求线段
AC
的长.
A
C
B
解
由题意,得
AB∶BC
=
BC∶AC
∵BC
=
AC
+2,
.
∴
.
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
