22.1比例线段 第4课时 平行线分线段成比例及其推论 课件(共21张PPT)
文档属性
| 名称 | 22.1比例线段 第4课时 平行线分线段成比例及其推论 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 16:58:38 | ||
图片预览




文档简介
(共21张PPT)
第4课时
平行线分线段成比例及其推论
22.1
比例线段
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
在理解的基础上掌握平行线分线段成比例定理及其推论.
【过程与方法】
通过学习定理再次锻炼类比的数学思想,能把一个稍复杂的图形分成几个基本图形,通过应用锻炼识图能力和推理论证能力.
【情感态度】
通过定理的学习知道认识事物的一般规律是从特殊到一般,并能欣赏数学表达式的对称美.
【教学重点】
定理的应用.
【教学难点】
定理的推导证明.
新课导入
说一说:什么是平行线等分线段定理?
如果一组平行线在一条直线截得的线段相等,那么在其他直线上截得的线段也相等.
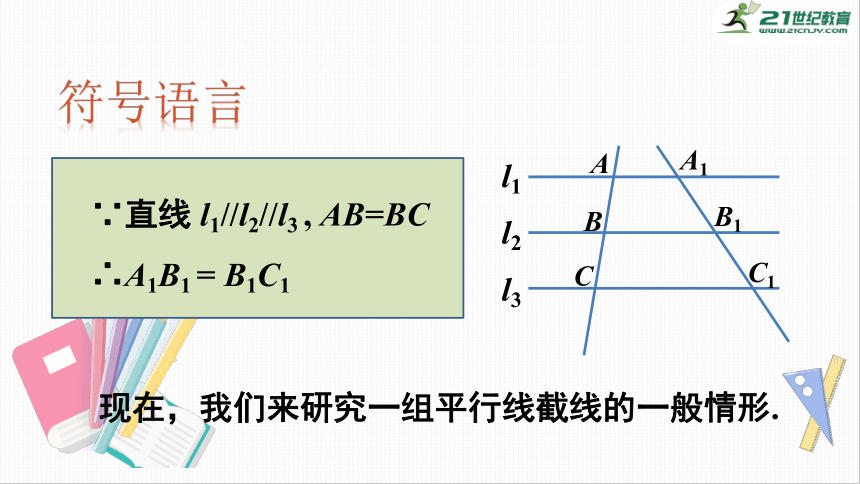
符号语言
∵直线
l1//l2//l3
,
AB=BC
∴A1B1
=
B1C1
l1
l2
l3
A
B
C
A1
B1
C1
现在,我们来研究一组平行线截线的一般情形.
新课探究
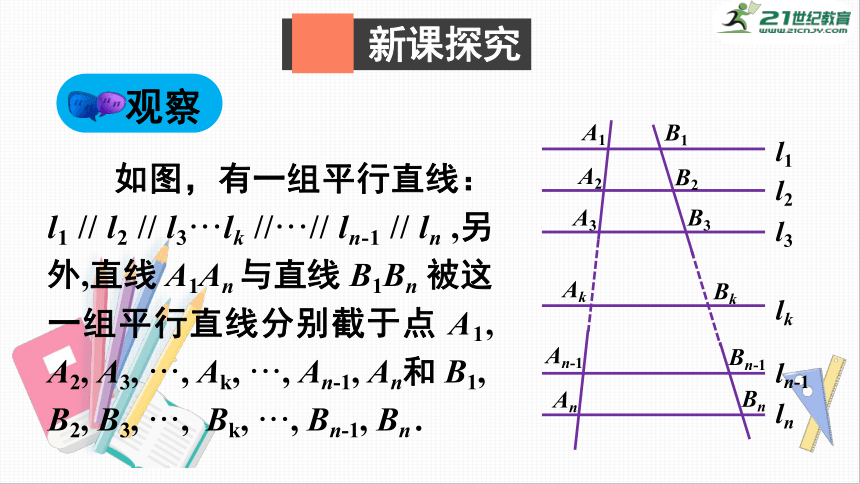
观察
如图,有一组平行直线:l1
//
l2
//
l3···lk
//···//
ln-1
//
ln
,另外,直线
A1An
与直线
B1Bn
被这一组平行直线分别截于点
A1,
A2,
A3,
···,
Ak,
···,
An-1,
An和
B1,
B2,
B3,
···,
Bk,
···,
Bn-1,
Bn
.
l1
l2
l3
lk
ln-1
ln
A1
A2
An
Ak
An-1
B2
B3
Bk
Bn-1
A3
Bn
B1
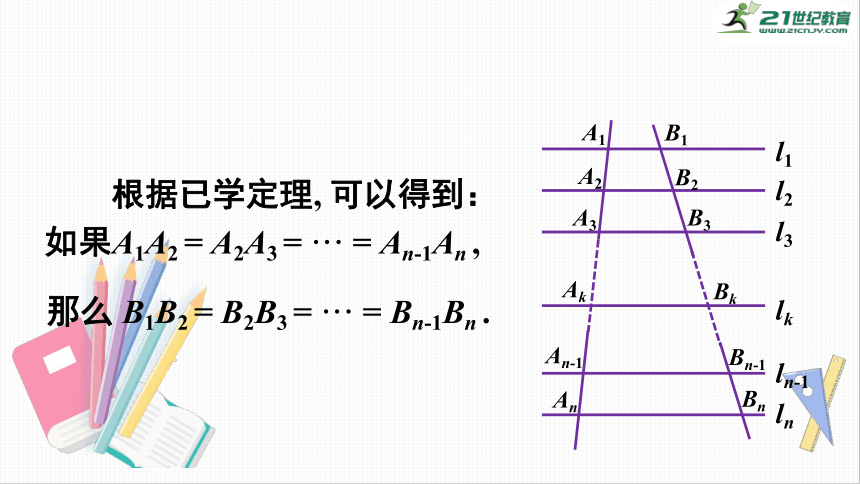
根据已学定理,
可以得到:如果A1A2
=
A2A3
=
···
=
An-1An
,
那么
B1B2
=
B2B3
=
···
=
Bn-1Bn
.
l1
l2
l3
lk
ln-1
ln
A1
A2
An
Ak
An-1
B2
B3
Bk
Bn-1
A3
Bn
B1
这时,
如设
A1A2
=
A2A3
=
···
=
An-1An
=
a
,
B1B2
=
B2B3
=
···
=
Bn-1Bn
=
b,
容易推得:
l1
l2
l3
lk
ln-1
ln
A1
A2
An
Ak
An-1
B2
B3
Bk
Bn-1
A3
Bn
B1
所以有
l1
l2
l3
lk
ln-1
ln
A1
A2
An
Ak
An-1
B2
B3
Bk
Bn-1
A3
Bn
B1
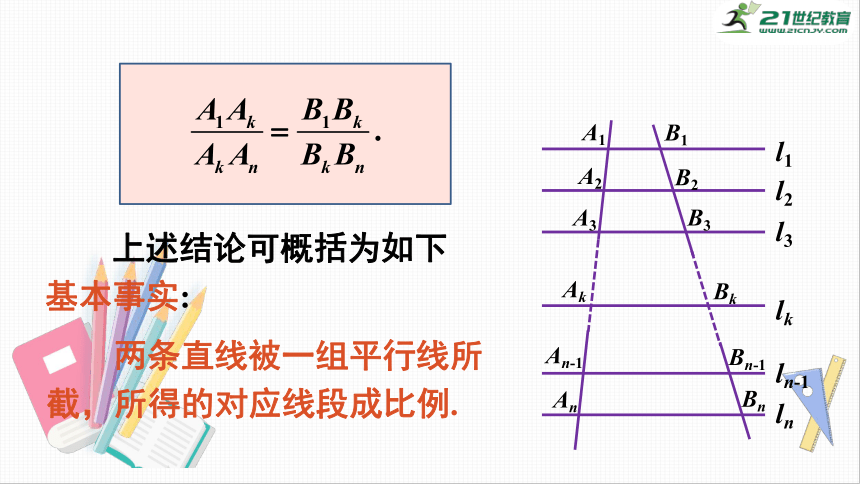
上述结论可概括为如下基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
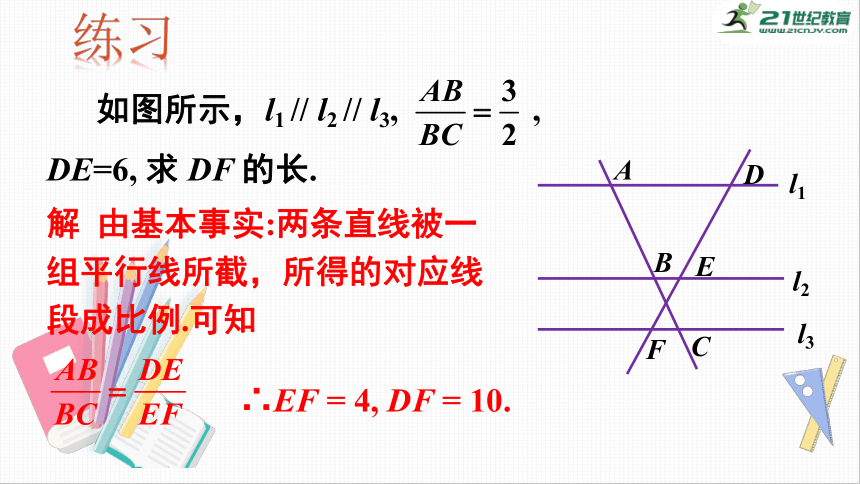
如图所示,l1
//
l2
//
l3,
,
DE=6,
求
DF
的长.
练习
l1
l2
l3
D
A
B
E
F
C
解
由基本事实:两条直线被一组平行线所截,所得的对应线段成比例.可知
∴EF
=
4,
DF
=
10.
下面看一个特例,如图,直线DE平行于△ABC的一边BC,并分别交另两边AB,AC(或它们延长线)于点D,E.根据上面基本事实,得
A
C
B
D
E
A
D
B
C
E
A
C
B
D
E
A
D
B
C
E
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
随堂演练
1.已知:如图,
DE
//
BC,
DE
分别交
AB、AC于点
D、E.
试说明:
.
A
D
B
C
E
解
∵DE//BC
∴
∵EF//AB
∴
A
D
B
C
E
作EF//AB交
BC
于F点.
F
又∵DE=BF
∴
2.如图,
△ABC中,
E,F
分别是
AB
和
AC
上的点,且
EF//BC.
(1)如图
AE=7,EB=5,FC=4,那么
AF
的长是多少?
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
F
E
B
C
A
F
E
B
C
解
(1)
∵EF//BC
,
∴
.
∴
.
AE=7,EB=5,FC=4,
又∵
(2)
∵EF//BC,
∴
.
AB=10,AE=6,AF=5.
又∵
∴
,
FC
=
AC
–
AF
=
.
∴
3.
如图,
△ABC
中,
DE
//
BC,
EF
//
CD.
试说明
AD
是
AB
和
AF
的比例中项.
A
E
D
B
C
F
分析:
分别在
△ABC
及△ADC
中利用平行线分线段成比例定理的推论.
A
E
D
B
C
F
解
∵在△ABC
中
,
DE
//
BC,
∴
.
∴
.
∴
.
∴
AD2
=AB·AF,
即AD是AB和AF
的比例中项.
又∵在△ADC
中
,
EF
//
CD,
课堂小结
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
两条直线被一组平行线所截,所得的对应线段成比例.
课后作业
1.完成课后的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第4课时
平行线分线段成比例及其推论
22.1
比例线段
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
在理解的基础上掌握平行线分线段成比例定理及其推论.
【过程与方法】
通过学习定理再次锻炼类比的数学思想,能把一个稍复杂的图形分成几个基本图形,通过应用锻炼识图能力和推理论证能力.
【情感态度】
通过定理的学习知道认识事物的一般规律是从特殊到一般,并能欣赏数学表达式的对称美.
【教学重点】
定理的应用.
【教学难点】
定理的推导证明.
新课导入
说一说:什么是平行线等分线段定理?
如果一组平行线在一条直线截得的线段相等,那么在其他直线上截得的线段也相等.
符号语言
∵直线
l1//l2//l3
,
AB=BC
∴A1B1
=
B1C1
l1
l2
l3
A
B
C
A1
B1
C1
现在,我们来研究一组平行线截线的一般情形.
新课探究
观察
如图,有一组平行直线:l1
//
l2
//
l3···lk
//···//
ln-1
//
ln
,另外,直线
A1An
与直线
B1Bn
被这一组平行直线分别截于点
A1,
A2,
A3,
···,
Ak,
···,
An-1,
An和
B1,
B2,
B3,
···,
Bk,
···,
Bn-1,
Bn
.
l1
l2
l3
lk
ln-1
ln
A1
A2
An
Ak
An-1
B2
B3
Bk
Bn-1
A3
Bn
B1
根据已学定理,
可以得到:如果A1A2
=
A2A3
=
···
=
An-1An
,
那么
B1B2
=
B2B3
=
···
=
Bn-1Bn
.
l1
l2
l3
lk
ln-1
ln
A1
A2
An
Ak
An-1
B2
B3
Bk
Bn-1
A3
Bn
B1
这时,
如设
A1A2
=
A2A3
=
···
=
An-1An
=
a
,
B1B2
=
B2B3
=
···
=
Bn-1Bn
=
b,
容易推得:
l1
l2
l3
lk
ln-1
ln
A1
A2
An
Ak
An-1
B2
B3
Bk
Bn-1
A3
Bn
B1
所以有
l1
l2
l3
lk
ln-1
ln
A1
A2
An
Ak
An-1
B2
B3
Bk
Bn-1
A3
Bn
B1
上述结论可概括为如下基本事实:
两条直线被一组平行线所截,所得的对应线段成比例.
如图所示,l1
//
l2
//
l3,
,
DE=6,
求
DF
的长.
练习
l1
l2
l3
D
A
B
E
F
C
解
由基本事实:两条直线被一组平行线所截,所得的对应线段成比例.可知
∴EF
=
4,
DF
=
10.
下面看一个特例,如图,直线DE平行于△ABC的一边BC,并分别交另两边AB,AC(或它们延长线)于点D,E.根据上面基本事实,得
A
C
B
D
E
A
D
B
C
E
A
C
B
D
E
A
D
B
C
E
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
随堂演练
1.已知:如图,
DE
//
BC,
DE
分别交
AB、AC于点
D、E.
试说明:
.
A
D
B
C
E
解
∵DE//BC
∴
∵EF//AB
∴
A
D
B
C
E
作EF//AB交
BC
于F点.
F
又∵DE=BF
∴
2.如图,
△ABC中,
E,F
分别是
AB
和
AC
上的点,且
EF//BC.
(1)如图
AE=7,EB=5,FC=4,那么
AF
的长是多少?
(2)如果AB=10,AE=6,AF=5,那么FC的长是多少?
A
F
E
B
C
A
F
E
B
C
解
(1)
∵EF//BC
,
∴
.
∴
.
AE=7,EB=5,FC=4,
又∵
(2)
∵EF//BC,
∴
.
AB=10,AE=6,AF=5.
又∵
∴
,
FC
=
AC
–
AF
=
.
∴
3.
如图,
△ABC
中,
DE
//
BC,
EF
//
CD.
试说明
AD
是
AB
和
AF
的比例中项.
A
E
D
B
C
F
分析:
分别在
△ABC
及△ADC
中利用平行线分线段成比例定理的推论.
A
E
D
B
C
F
解
∵在△ABC
中
,
DE
//
BC,
∴
.
∴
.
∴
.
∴
AD2
=AB·AF,
即AD是AB和AF
的比例中项.
又∵在△ADC
中
,
EF
//
CD,
课堂小结
推论
平行于三角形一边的直线截其他两边(或两边延长线),所得的对应线段成比例.
两条直线被一组平行线所截,所得的对应线段成比例.
课后作业
1.完成课后的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
