22.2相似三角形的判定 第5课时 直角三角形相似的判定方法 课件(共20张PPT)
文档属性
| 名称 | 22.2相似三角形的判定 第5课时 直角三角形相似的判定方法 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 19:26:02 | ||
图片预览




文档简介
(共20张PPT)
第5课时
直角三角形相似的判定方法
22.2
相似三角形的判定
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
经历直角三角形相似的判定定理的探索及证明过程.
【过程与方法】
让学生经历观察、实验、猜想、证明的过程,培养学生提出问题、分析问题、解决问题的能力.
【情感态度】
通过学生积极参与,激发学生学习数学的兴趣,体验数学探索与创造的快乐.
【教学重点】
三角形相似的判定定理及应用.
【教学难点】
三角形相似的判定定理及应用.
新课导入
到目前为止我们总共学过几种判定两个三角形相似的方法?
判定定理1
两角对应相等的两个三角形相似.
判定定理2
两边对应成比例且夹角相等的两个
三角形相似.
判定定理3
三边对应成比例的两个三角形相似.
思考
两个等腰三角形一定相似吗?两个等边三角形、两个直角三角形呢?
新课探究
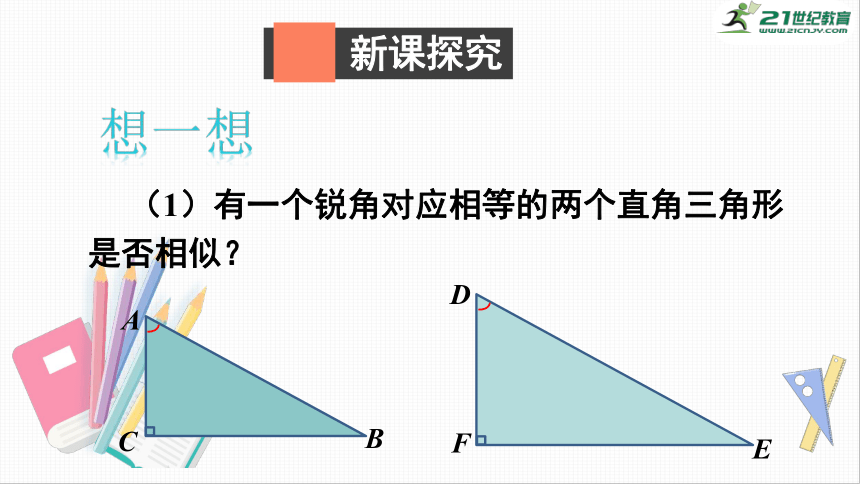
(1)有一个锐角对应相等的两个直角三角形是否相似?
想一想
A
B
C
D
E
F
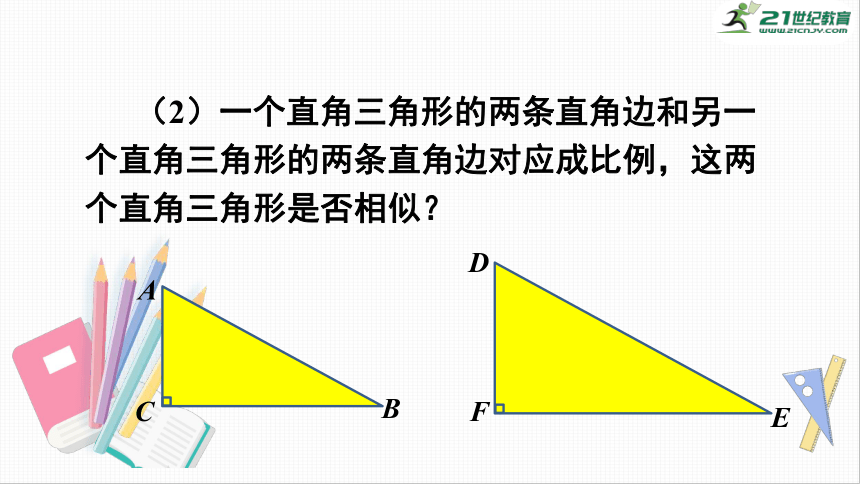
(2)一个直角三角形的两条直角边和另一个直角三角形的两条直角边对应成比例,这两个直角三角形是否相似?
A
B
C
D
E
F
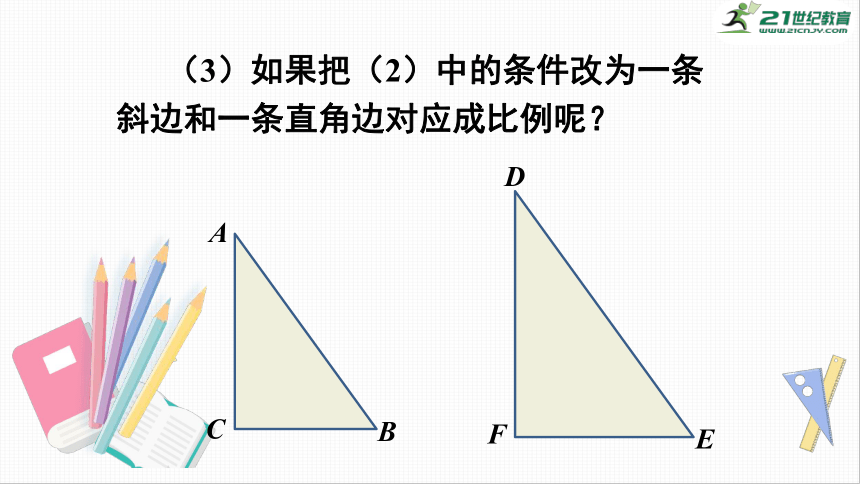
(3)如果把(2)中的条件改为一条斜边和一条直角边对应成比例呢?
A
B
C
D
E
F
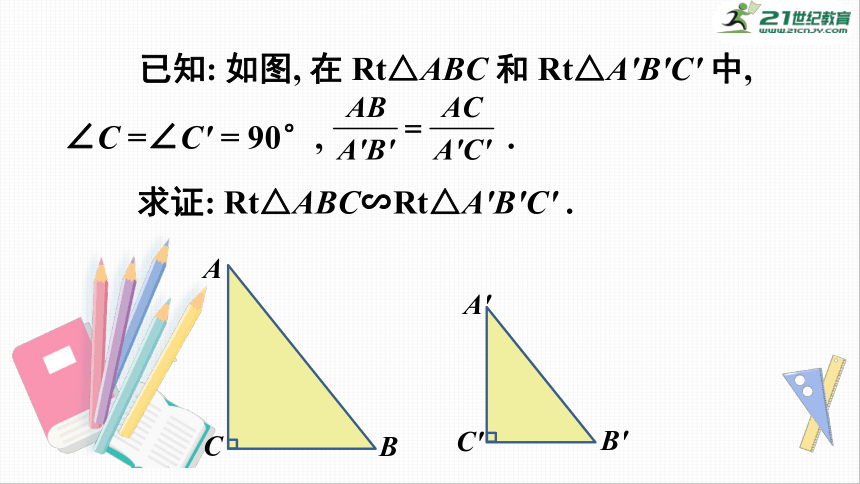
已知:
如图,
在
Rt△ABC
和
Rt△A′B′C′
中,
∠C
=∠C′
=
90°,
.
求证:
Rt△ABC∽Rt△A′B′C′
.
A
C
B
B′
A′
C′
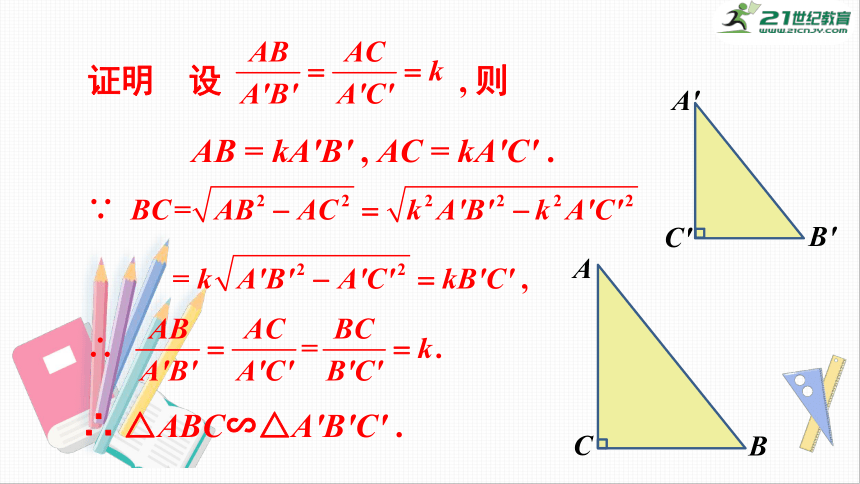
证明
设
,
则
AB
=
kA′B′
,
AC
=
kA′C′
.
∴
△ABC∽△A′B′C′
.
A
C
B
B′
A′
C′
直角三角形相似的判定方法
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
例4
如图,
∠ABC
=∠CDB
=
90°,
CB
=
a,
AC
=
b.
问当
BD
与
a,
b
之间满足怎样的函数表达式时,
以点
A,
B,
C
为顶点的三角形与以点
C,
D
,
B
为顶点的三角形相似?
A
B
D
C
a
b
解
∵
∠ABC=∠CDB=90°,
当
时,
△ABC∽△CDB.
即
又当
时,
△ABC∽△BDC.
A
B
D
C
a
b
即
答:
当
或
时,
以点
A,
B,
C
为顶点的三角形与以点
C,
D,
B
为顶点的三角形相似.
随堂演练
1.
锐角三角形ABC
的边
AB,
AC
上的高
CE,
BF相交于点
D,
请写出图中的两对相似三角形.
A
B
C
E
F
D
△BED
∽△CFD.
△BED
∽△BFA.
2.
在
Rt△ABC
与△A′B′C′中,∠C
=∠C′
=
90°,
当具有下列条件时,
这两个直角三角形是否相似,
为什么?
(1)AB=10cm,
AC=8cm,
A′B′=15cm,
B′C′=9cm;
(2)AB=5cm,
AC=4cm,
A′C′=12cm,
B′C′=9cm.
(1)AB=10cm,
AC=8cm,
A′B′=15cm,
B′C′=9cm;
解
由勾股定理得
A′C′=12
cm,
B
A
C
∵
∴
∴△ABC
∽△A′B′C′.
A′
C′
B′
(2)AB=5cm,
AC=4cm,
A′C′=12cm,
B′C′=9cm.
解
由勾股定理得
A′B′=15
cm,
B
A
C
∵
∴
∴△ABC
∽△A′B′C′.
A′
C′
B′
课堂小结
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
判断直角三角形相似的方法:
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第5课时
直角三角形相似的判定方法
22.2
相似三角形的判定
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
经历直角三角形相似的判定定理的探索及证明过程.
【过程与方法】
让学生经历观察、实验、猜想、证明的过程,培养学生提出问题、分析问题、解决问题的能力.
【情感态度】
通过学生积极参与,激发学生学习数学的兴趣,体验数学探索与创造的快乐.
【教学重点】
三角形相似的判定定理及应用.
【教学难点】
三角形相似的判定定理及应用.
新课导入
到目前为止我们总共学过几种判定两个三角形相似的方法?
判定定理1
两角对应相等的两个三角形相似.
判定定理2
两边对应成比例且夹角相等的两个
三角形相似.
判定定理3
三边对应成比例的两个三角形相似.
思考
两个等腰三角形一定相似吗?两个等边三角形、两个直角三角形呢?
新课探究
(1)有一个锐角对应相等的两个直角三角形是否相似?
想一想
A
B
C
D
E
F
(2)一个直角三角形的两条直角边和另一个直角三角形的两条直角边对应成比例,这两个直角三角形是否相似?
A
B
C
D
E
F
(3)如果把(2)中的条件改为一条斜边和一条直角边对应成比例呢?
A
B
C
D
E
F
已知:
如图,
在
Rt△ABC
和
Rt△A′B′C′
中,
∠C
=∠C′
=
90°,
.
求证:
Rt△ABC∽Rt△A′B′C′
.
A
C
B
B′
A′
C′
证明
设
,
则
AB
=
kA′B′
,
AC
=
kA′C′
.
∴
△ABC∽△A′B′C′
.
A
C
B
B′
A′
C′
直角三角形相似的判定方法
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
例4
如图,
∠ABC
=∠CDB
=
90°,
CB
=
a,
AC
=
b.
问当
BD
与
a,
b
之间满足怎样的函数表达式时,
以点
A,
B,
C
为顶点的三角形与以点
C,
D
,
B
为顶点的三角形相似?
A
B
D
C
a
b
解
∵
∠ABC=∠CDB=90°,
当
时,
△ABC∽△CDB.
即
又当
时,
△ABC∽△BDC.
A
B
D
C
a
b
即
答:
当
或
时,
以点
A,
B,
C
为顶点的三角形与以点
C,
D,
B
为顶点的三角形相似.
随堂演练
1.
锐角三角形ABC
的边
AB,
AC
上的高
CE,
BF相交于点
D,
请写出图中的两对相似三角形.
A
B
C
E
F
D
△BED
∽△CFD.
△BED
∽△BFA.
2.
在
Rt△ABC
与△A′B′C′中,∠C
=∠C′
=
90°,
当具有下列条件时,
这两个直角三角形是否相似,
为什么?
(1)AB=10cm,
AC=8cm,
A′B′=15cm,
B′C′=9cm;
(2)AB=5cm,
AC=4cm,
A′C′=12cm,
B′C′=9cm.
(1)AB=10cm,
AC=8cm,
A′B′=15cm,
B′C′=9cm;
解
由勾股定理得
A′C′=12
cm,
B
A
C
∵
∴
∴△ABC
∽△A′B′C′.
A′
C′
B′
(2)AB=5cm,
AC=4cm,
A′C′=12cm,
B′C′=9cm.
解
由勾股定理得
A′B′=15
cm,
B
A
C
∵
∴
∴△ABC
∽△A′B′C′.
A′
C′
B′
课堂小结
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
判断直角三角形相似的方法:
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
