22.3 相似三角形的性质 第2课时 相似三角形的性质定理2,3 课件(共22张PPT)
文档属性
| 名称 | 22.3 相似三角形的性质 第2课时 相似三角形的性质定理2,3 课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-09 21:10:34 | ||
图片预览



文档简介
(共22张PPT)
第2课时
相似三角形的性质定理2,3
22.3
相似三角形的性质
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
能运用相似三角形的性质解决一些简单的实际问题.
【过程与方法】
通过例题的教学,让学生掌握解决实际问题的方法.
【情感态度】
进一步检验数学的应用价值.
【教学重点】
运用相似三角形的性质解决简单的实际问题.
【教学难点】
运用相似三角形的性质解决简单的实际问题.
新课导入
1.相似三角形对应线段的比等于_______.
2.相似三角形对应高的比、对应中线的比与对应角平分线的比都等于_______.
相似比
相似比
新课探究
思考
相似三角形周长的比和面积的比分别与相似比有什么关系?
A
B
C
C′
A′
B′
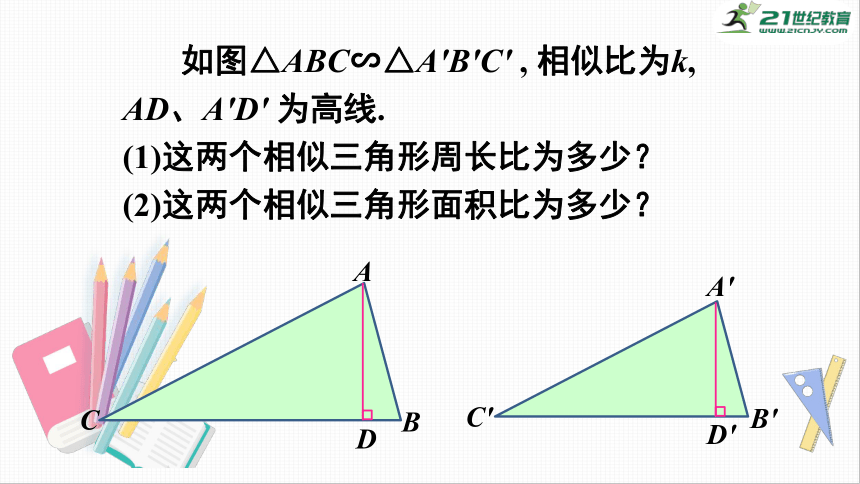
如图△ABC∽△A′B′C′
,
相似比为k,
AD、A′D′
为高线.
(1)这两个相似三角形周长比为多少?
(2)这两个相似三角形面积比为多少?
C
B
A
D
A′
C′
B′
D′
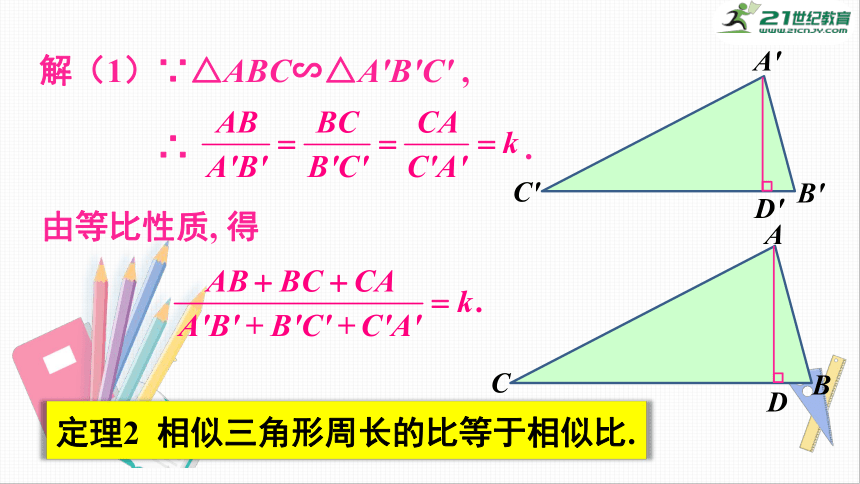
解(1)∵△ABC∽△A′B′C′
,
∴
.
由等比性质,
得
A′
C′
B′
D′
C
B
A
D
定理2
相似三角形周长的比等于相似比.
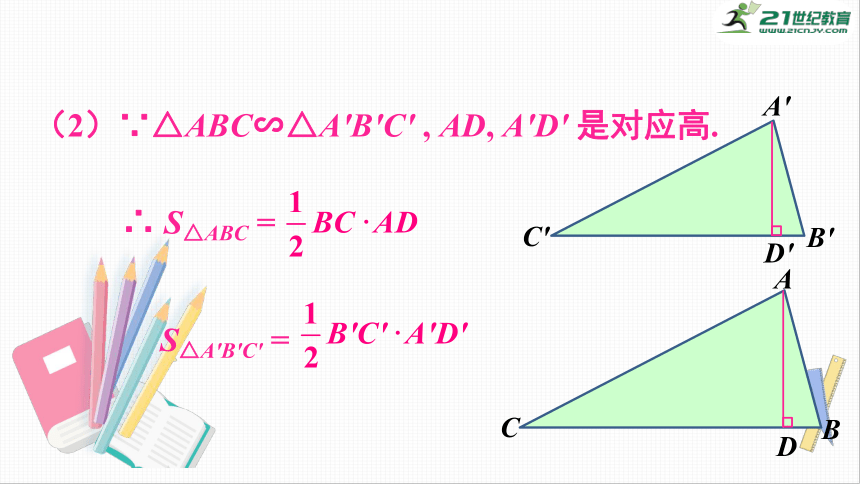
(2)∵△ABC∽△A′B′C′
,
AD,
A′D′
是对应高.
∴
S△ABC
=
S△A′B′C′
=
A′
C′
B′
D′
C
B
A
D
S△ABC
S△A′B′C′
=
=
=
k2
A′
C′
B′
D′
C
B
A
D
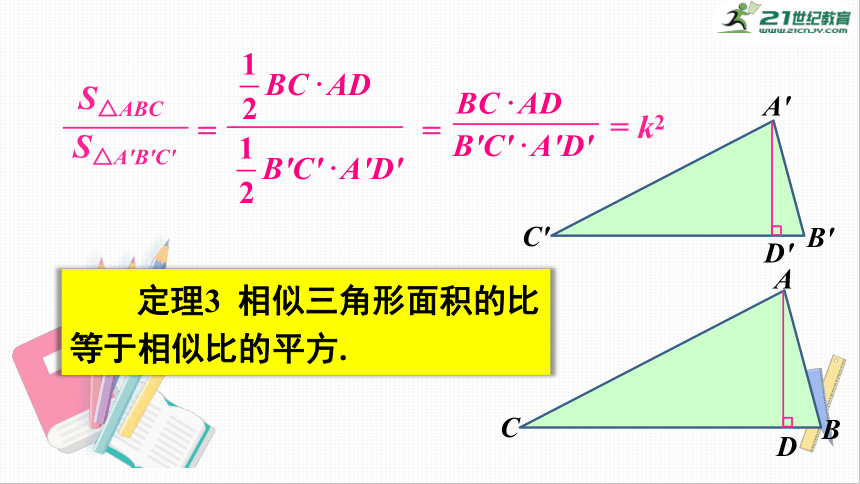
定理3
相似三角形面积的比等于相似比的平方.
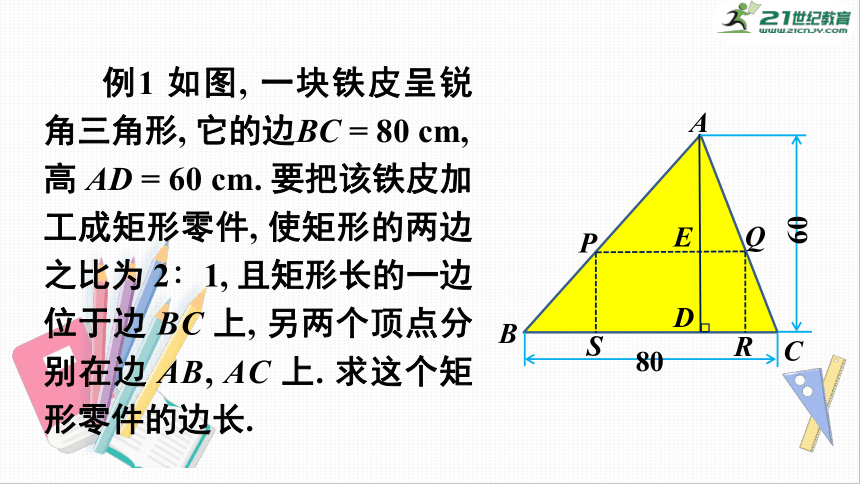
例1
如图,
一块铁皮呈锐角三角形,
它的边BC
=
80
cm,
高
AD
=
60
cm.
要把该铁皮加工成矩形零件,
使矩形的两边之比为
2∶1,
且矩形长的一边位于边
BC
上,
另两个顶点分别在边
AB,
AC
上.
求这个矩形零件的边长.
B
C
80
60
P
Q
E
S
R
A
D
解
如图,
矩形
PQRS
为加工后的矩形零件,
边SR在边BC上,
顶点
P,
Q
分别在边AB,
AC
上,
△ABC
的高
AD
交PQ于点E.设PS为为
x
cm,
则
PQ
为
2x
cm.
B
C
80
60
P
Q
E
S
R
A
D
∵
PQ
//
BC
,
∴
△APQ∽△ABC.
∴
即
解方程,
得
x
=
24,
2x
=
48.
答:
这个矩形零件的边长分别是
48
cm和
24
cm.
B
C
80
60
P
Q
E
S
R
A
D
例2
如图,
△ABC
的面积为
25,
直线
DE
平行于
BC
分别交
AB,
AC
于点
D,
E.
如果△ADE的面积为
9,
求
的值.
A
D
B
C
E
解
∵
DE
//
BC
,
∴
△ADE∽△ABC.
∴
解方程,
得
∴
A
D
B
C
E
随堂演练
1.
两个相似三角形对应边比为
3:5,
那么相似比为______,
周长比为______,
面积比为______.
3∶5
3∶5
9∶25
2.
如图,
在正方形网格上有△A1B1C1
和
△A2B2C2,
这两个三角形相似吗?
如果相似,
求出△A1B1C1和△A2B2C2
的面积比.
A1
A2
B2
C2
B1
C1
相似,
相似比为2:1
面积比为
4:1
4.已知
△ABC∽△A′B′C′
,
AC
:
A′C′
=
4:3.
(1)若△ABC
的周长为
24
cm,
则△A′B′C′
的周长为____cm;
(2)若△ABC
的面积为
32
cm2
,
则△A′B′C′的面积为____cm2.
18
18
5.
如图,
已知
DE∥BC,
BD
=
3AD,
S△ABC
=
48,
求:
△ADE
的面积.
D
E
B
C
A
解
∵
DE∥BC
,
∴∠ADE
=∠ABC,
∠AED
=∠ACB.
∴△ADE∽△ABC.
可得相似比
∴
D
E
B
C
A
又∵
BD
=
3AD
,
课堂小结
相似三角形的性质
(1)对应角相等、对应边成比例
(2)对应高之比、对应中线之比、对应角平分线之比都等于相似比
(3)周长之比等于相似比
(4)面积之比等于相似比的平方
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第2课时
相似三角形的性质定理2,3
22.3
相似三角形的性质
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
能运用相似三角形的性质解决一些简单的实际问题.
【过程与方法】
通过例题的教学,让学生掌握解决实际问题的方法.
【情感态度】
进一步检验数学的应用价值.
【教学重点】
运用相似三角形的性质解决简单的实际问题.
【教学难点】
运用相似三角形的性质解决简单的实际问题.
新课导入
1.相似三角形对应线段的比等于_______.
2.相似三角形对应高的比、对应中线的比与对应角平分线的比都等于_______.
相似比
相似比
新课探究
思考
相似三角形周长的比和面积的比分别与相似比有什么关系?
A
B
C
C′
A′
B′
如图△ABC∽△A′B′C′
,
相似比为k,
AD、A′D′
为高线.
(1)这两个相似三角形周长比为多少?
(2)这两个相似三角形面积比为多少?
C
B
A
D
A′
C′
B′
D′
解(1)∵△ABC∽△A′B′C′
,
∴
.
由等比性质,
得
A′
C′
B′
D′
C
B
A
D
定理2
相似三角形周长的比等于相似比.
(2)∵△ABC∽△A′B′C′
,
AD,
A′D′
是对应高.
∴
S△ABC
=
S△A′B′C′
=
A′
C′
B′
D′
C
B
A
D
S△ABC
S△A′B′C′
=
=
=
k2
A′
C′
B′
D′
C
B
A
D
定理3
相似三角形面积的比等于相似比的平方.
例1
如图,
一块铁皮呈锐角三角形,
它的边BC
=
80
cm,
高
AD
=
60
cm.
要把该铁皮加工成矩形零件,
使矩形的两边之比为
2∶1,
且矩形长的一边位于边
BC
上,
另两个顶点分别在边
AB,
AC
上.
求这个矩形零件的边长.
B
C
80
60
P
Q
E
S
R
A
D
解
如图,
矩形
PQRS
为加工后的矩形零件,
边SR在边BC上,
顶点
P,
Q
分别在边AB,
AC
上,
△ABC
的高
AD
交PQ于点E.设PS为为
x
cm,
则
PQ
为
2x
cm.
B
C
80
60
P
Q
E
S
R
A
D
∵
PQ
//
BC
,
∴
△APQ∽△ABC.
∴
即
解方程,
得
x
=
24,
2x
=
48.
答:
这个矩形零件的边长分别是
48
cm和
24
cm.
B
C
80
60
P
Q
E
S
R
A
D
例2
如图,
△ABC
的面积为
25,
直线
DE
平行于
BC
分别交
AB,
AC
于点
D,
E.
如果△ADE的面积为
9,
求
的值.
A
D
B
C
E
解
∵
DE
//
BC
,
∴
△ADE∽△ABC.
∴
解方程,
得
∴
A
D
B
C
E
随堂演练
1.
两个相似三角形对应边比为
3:5,
那么相似比为______,
周长比为______,
面积比为______.
3∶5
3∶5
9∶25
2.
如图,
在正方形网格上有△A1B1C1
和
△A2B2C2,
这两个三角形相似吗?
如果相似,
求出△A1B1C1和△A2B2C2
的面积比.
A1
A2
B2
C2
B1
C1
相似,
相似比为2:1
面积比为
4:1
4.已知
△ABC∽△A′B′C′
,
AC
:
A′C′
=
4:3.
(1)若△ABC
的周长为
24
cm,
则△A′B′C′
的周长为____cm;
(2)若△ABC
的面积为
32
cm2
,
则△A′B′C′的面积为____cm2.
18
18
5.
如图,
已知
DE∥BC,
BD
=
3AD,
S△ABC
=
48,
求:
△ADE
的面积.
D
E
B
C
A
解
∵
DE∥BC
,
∴∠ADE
=∠ABC,
∠AED
=∠ACB.
∴△ADE∽△ABC.
可得相似比
∴
D
E
B
C
A
又∵
BD
=
3AD
,
课堂小结
相似三角形的性质
(1)对应角相等、对应边成比例
(2)对应高之比、对应中线之比、对应角平分线之比都等于相似比
(3)周长之比等于相似比
(4)面积之比等于相似比的平方
课后作业
1.完成课本的练习;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
