22.4图形的位似变换 第1课时 位似图形 课件(共27张PPT)
文档属性
| 名称 | 22.4图形的位似变换 第1课时 位似图形 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
第1课时
位似图形
22.4
图形的位似变换
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
1.了解图形的位似概念,会判断简单的位似图形和位似中心.
2.理解位似图形的性质,能利用位似将一个图形放大或缩小,解决一些简单的实际问题.
【过程与方法】
采用引导、启发、合作、探究等方法,经历观察、发现、动手操作、归纳、交流等数学活动,获得知识,形成技能,发展思维,学会学习.
【情感态度】
使学生亲身经历位似图形概念形成的过程和位似图形性质的探索过程,感受数学学习内容的现实性、应用性.
【教学重点】
图形的位似概念、位似图形的性质及利用位似把一个图形放大或缩小.
【教学难点】
探索位似概念、位似图形的性质的过程及利用位似准确地把一个图形通过不同的方法放大或缩小.
新课导入
在日常生活中,
有时需要把一个图形放大或缩小.
例如,
在放映机上放映幻灯片时,
把幻灯片上的图象放大到屏幕上;
在照相馆里,
摄影师通过照相机把实物的图象缩小在底片上.
这样放大或缩小的图形,
形状_____,
大小_____,
所以它们_____.
相同
不同
相似
新课探究
例1
把四边形
ABCD
放大为原来的
2
倍(即新图与原图的相似比为
2).
A
B
C
D
A
B
C
D
A′
O
D′
C′
B′
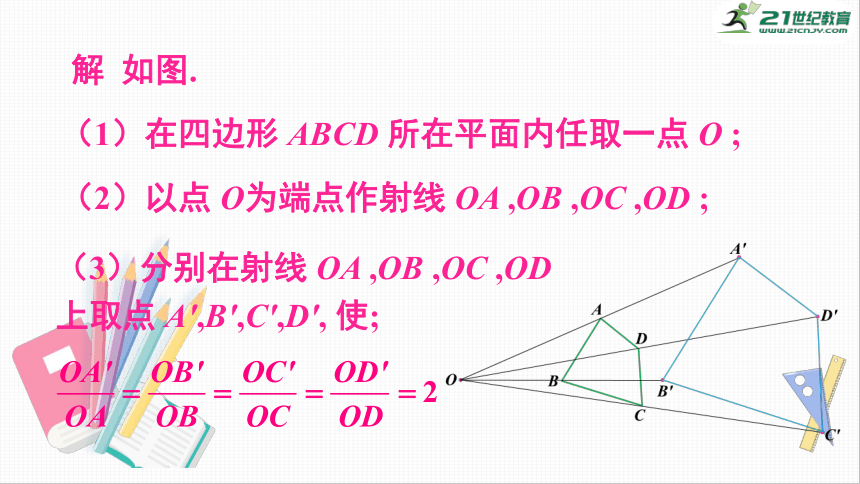
解
如图.
(1)在四边形
ABCD
所在平面内任取一点
O
;
(2)以点
O为端点作射线
OA
,OB
,OC
,OD
;
(3)分别在射线
OA
,OB
,OC
,OD
上取点
A′,B′,C′,D′,
使;
(4)连接
A′B′,B′C′
,C′D′
,D′A′
.
所得四边形A′B′C′D′
即为所求.
例1
把四边形
ABCD
放大为原来的
2
倍(即新图与原图的相似比为
2).
A
B
C
D
想一想
本题还有其他的方法作图吗?
A
B
C
D
O
A′
B′
D′
C′
思
考
下图中所得四边形A′B′C′D′∽四边形ACBD,
你能说明道理吗?
一般地,
如果一个图形上的
A1,
B1,
···,
P1
和另一个图形上的点
A,
B,
···,
P
分别对应,
并且满足下面两点:
说一说什么是位似图形?
(1)直线
AA1,
BB1,
···,
PP1
都经过同一点
O
;
(2)
那么,
这两个图形叫做位似图形,
点
O
叫做位似中心.
图形的位似,
也可用于把图形缩小,
如用小平板仪测绘小范围区域时,
就是这样做的.
例2
如图,
四边形
ABCD
是一个待测绘的小区.
在区内选一个测绘点O,
A
B
C
D
O
A
B
C
D
O
将图板上测绘图纸的点O1对准测绘点
O,
再由O1对准点
A
,B
,C
,D
在纸上作射线
O1A,
O1B,
O1C,
O1D,
O1
A
B
C
D
O
分别测得点O到点
A,
B,
C,
D
的距离,
并按同一比例缩小,
在图纸的对应射线上定出点
A1
,B1
,C1
,D1
,
O1
B1
A1
C1
D1
依次连接
A1B1
,B1C1
,C1D1
,D1A1
,
即得该小区缩小的平面图.
A
B
C
D
O
O1
B1
A1
C1
D1
(1)位似图形是相似图形的特殊情形.
(2)位似图形必定是相似图形,而相似图形不一定是位似图形.
(3)两个位似图形的位似中心只有一个.
(4)两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧.
注
意
随堂演练
1.
作一个五边形和已知五边形位似,
要求:
(1)位似中心取在已知五边形的一个顶点处,
相似比为
;
(2)位似中心取在已知五边形的一边上,相似比为3.
(1)位似中心取在已知五边形的一个顶点处,
相似比为
;
A
B
C
D
E
A1
B1
D1
E1
0
CA1
=
CA
CB1
=
CB
CD1
=
CD
CE1
=
CE
(2)位似中心取在已知五边形的一边上,
相似比为3.
A
B
D
E
E1
A1
B1
C1
C
D1
O
课堂小结
如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比。
位似图形、位似中心、位似比:
位似图形的性质:
位似图形上的任意一对对应点到位似中心的距离之比等于位似比.
画出基本图形.
选取位似中心.
根据条件确定对应点,并描出对应点.
顺次连结各对应点,所成的图形就是所求的图形.
位似图形的画法:
课后作业
1.从教材习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第1课时
位似图形
22.4
图形的位似变换
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
1.了解图形的位似概念,会判断简单的位似图形和位似中心.
2.理解位似图形的性质,能利用位似将一个图形放大或缩小,解决一些简单的实际问题.
【过程与方法】
采用引导、启发、合作、探究等方法,经历观察、发现、动手操作、归纳、交流等数学活动,获得知识,形成技能,发展思维,学会学习.
【情感态度】
使学生亲身经历位似图形概念形成的过程和位似图形性质的探索过程,感受数学学习内容的现实性、应用性.
【教学重点】
图形的位似概念、位似图形的性质及利用位似把一个图形放大或缩小.
【教学难点】
探索位似概念、位似图形的性质的过程及利用位似准确地把一个图形通过不同的方法放大或缩小.
新课导入
在日常生活中,
有时需要把一个图形放大或缩小.
例如,
在放映机上放映幻灯片时,
把幻灯片上的图象放大到屏幕上;
在照相馆里,
摄影师通过照相机把实物的图象缩小在底片上.
这样放大或缩小的图形,
形状_____,
大小_____,
所以它们_____.
相同
不同
相似
新课探究
例1
把四边形
ABCD
放大为原来的
2
倍(即新图与原图的相似比为
2).
A
B
C
D
A
B
C
D
A′
O
D′
C′
B′
解
如图.
(1)在四边形
ABCD
所在平面内任取一点
O
;
(2)以点
O为端点作射线
OA
,OB
,OC
,OD
;
(3)分别在射线
OA
,OB
,OC
,OD
上取点
A′,B′,C′,D′,
使;
(4)连接
A′B′,B′C′
,C′D′
,D′A′
.
所得四边形A′B′C′D′
即为所求.
例1
把四边形
ABCD
放大为原来的
2
倍(即新图与原图的相似比为
2).
A
B
C
D
想一想
本题还有其他的方法作图吗?
A
B
C
D
O
A′
B′
D′
C′
思
考
下图中所得四边形A′B′C′D′∽四边形ACBD,
你能说明道理吗?
一般地,
如果一个图形上的
A1,
B1,
···,
P1
和另一个图形上的点
A,
B,
···,
P
分别对应,
并且满足下面两点:
说一说什么是位似图形?
(1)直线
AA1,
BB1,
···,
PP1
都经过同一点
O
;
(2)
那么,
这两个图形叫做位似图形,
点
O
叫做位似中心.
图形的位似,
也可用于把图形缩小,
如用小平板仪测绘小范围区域时,
就是这样做的.
例2
如图,
四边形
ABCD
是一个待测绘的小区.
在区内选一个测绘点O,
A
B
C
D
O
A
B
C
D
O
将图板上测绘图纸的点O1对准测绘点
O,
再由O1对准点
A
,B
,C
,D
在纸上作射线
O1A,
O1B,
O1C,
O1D,
O1
A
B
C
D
O
分别测得点O到点
A,
B,
C,
D
的距离,
并按同一比例缩小,
在图纸的对应射线上定出点
A1
,B1
,C1
,D1
,
O1
B1
A1
C1
D1
依次连接
A1B1
,B1C1
,C1D1
,D1A1
,
即得该小区缩小的平面图.
A
B
C
D
O
O1
B1
A1
C1
D1
(1)位似图形是相似图形的特殊情形.
(2)位似图形必定是相似图形,而相似图形不一定是位似图形.
(3)两个位似图形的位似中心只有一个.
(4)两个位似图形可能位于位似中心的两侧,也可能位于位似中心的一侧.
注
意
随堂演练
1.
作一个五边形和已知五边形位似,
要求:
(1)位似中心取在已知五边形的一个顶点处,
相似比为
;
(2)位似中心取在已知五边形的一边上,相似比为3.
(1)位似中心取在已知五边形的一个顶点处,
相似比为
;
A
B
C
D
E
A1
B1
D1
E1
0
CA1
=
CA
CB1
=
CB
CD1
=
CD
CE1
=
CE
(2)位似中心取在已知五边形的一边上,
相似比为3.
A
B
D
E
E1
A1
B1
C1
C
D1
O
课堂小结
如果两个图形不仅相似,而且每组对应顶点所在的直线都经过同一个点,那么这样的两个图形叫做位似图形,这个点叫做位似中心,这时的相似比又称为位似比。
位似图形、位似中心、位似比:
位似图形的性质:
位似图形上的任意一对对应点到位似中心的距离之比等于位似比.
画出基本图形.
选取位似中心.
根据条件确定对应点,并描出对应点.
顺次连结各对应点,所成的图形就是所求的图形.
位似图形的画法:
课后作业
1.从教材习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
