22.4图形的位似变换 第2课时 平面直角坐标系中图形的位似变换 课件(共26张PPT)
文档属性
| 名称 | 22.4图形的位似变换 第2课时 平面直角坐标系中图形的位似变换 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 16:59:08 | ||
图片预览





文档简介
(共26张PPT)
第2课时
平面直角坐标系中图形的位似变换
22.4
图形的位似变换
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
1.了解图形的位似概念,会判断简单的位似图形和位似中心.
2.理解位似图形的性质,能利用位似将一个图形放大或缩小,解决一些简单的实际问题.
【过程与方法】
采用引导、启发、合作、探究等方法,经历观察、发现、动手操作、归纳、交流等数学活动,获得知识,形成技能,发展思维,学会学习.
【情感态度】
使学生亲身经历位似图形概念形成的过程和位似图形性质的探索过程,感受数学学习内容的现实性、应用性.
【教学重点】
图形的位似概念、位似图形的性质及利用位似把一个图形放大或缩小.
【教学难点】
探索位似概念、位似图形的性质的过程及利用位似准确地把一个图形通过不同的方法放大或缩小.
新课导入
位似图形的定义:
如果两个图形不仅是相似图形,
而且每组对应点所在的直线都经过同一个点,
那么这样的两个图形叫做位似图形,
这个点叫做位似中心,这时的相似比又称为位似比.
画位似图形的步骤:
(1)确定位似中心点;
(2)将图形各顶点与位似中心连接(或延长);
(3)按位似比进行取点;
(4)顺次连接各点,所得的图形就是所求的图形.
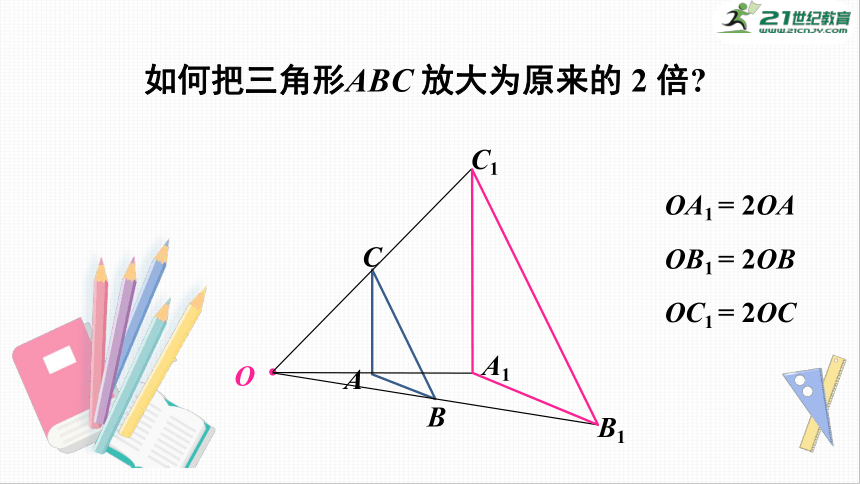
如何把三角形ABC
放大为原来的
2
倍?
A
B
C
O
B1
A1
C1
OA1
=
2OA
OB1
=
2OB
OC1
=
2OC
新课探究
交流
如果把位似图形放到直角坐标系中,又如何去探究位似变换与坐标之间的关系呢?
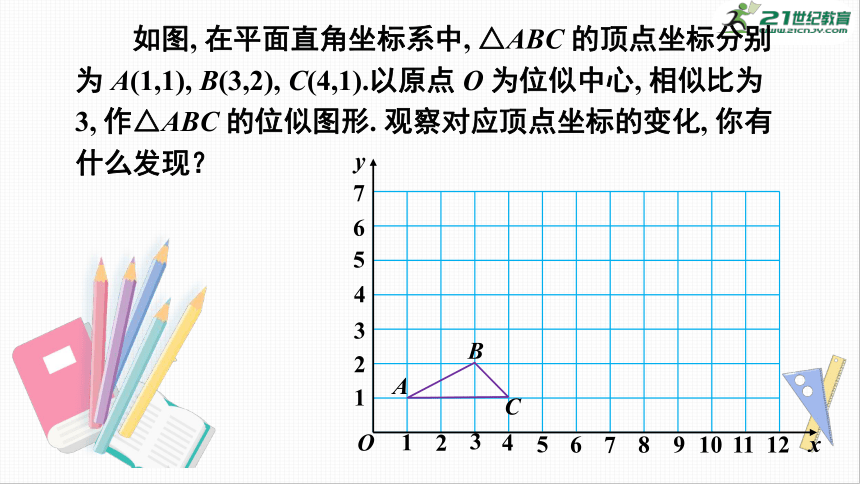
如图,
在平面直角坐标系中,
△ABC
的顶点坐标分别为
A(1,1),
B(3,2),
C(4,1).以原点
O
为位似中心,
相似比为3,
作△ABC
的位似图形.
观察对应顶点坐标的变化,
你有什么发现?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
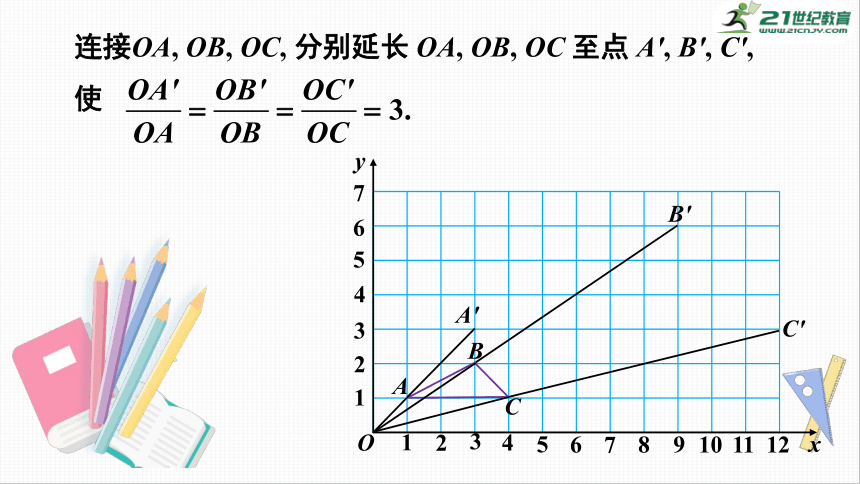
连接OA,
OB,
OC,
分别延长
OA,
OB,
OC
至点
A′,
B′,
C′,
使
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
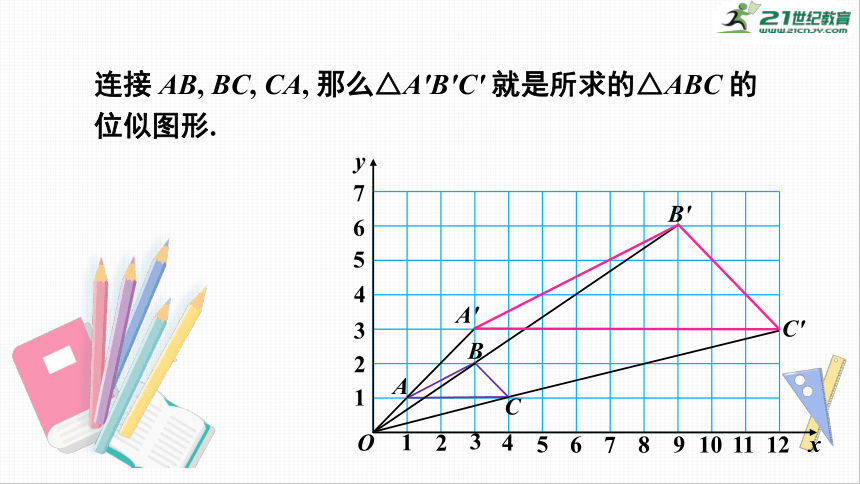
连接
AB,
BC,
CA,
那么△A′B′C′
就是所求的△ABC
的位似图形.
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
可以看到,
位似变换后点
A,
B,
C
的对应点分别为点A′(3,3)
,B′(9,6)
,C′(12,3).
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
对比下图中变换前后各对应点的坐标,你可以发现什么?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
在平面直角坐标系中,
如果位似变换是以原点
O
为位似中心,
相似比为
k(k>0),
原图形上点的坐标为(x,y),
那么同向位似图形对应点的坐标为(kx,
ky)(k>0).
利用这个性质作同向位似图形就相当简单,
只要把图形上各点的坐标都乘以一个固定的数
k(k>0),
就可以得到相似比为k(k>0)的同向位似图形.
O
x
y
A
B
C
B′
A′
C′
取
k
=3,
对图中的△ABC
进行变换,
看看结果如何?
这样得到的图形叫做反向位似图形.
O
x
y
A
B
C
B′
A′
C′
想一想:它与
k
=
3
时的变换结果有什么不同?
思考1:
将图中的△ABC,
按(x,
y)→
的方式变换,
求变换后所得图形中对应点的坐标.画出变换后图形,
它与原图形有何关系?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
A′
B′
C′
思考2:
将图中的△ABC,
按(x,
y)→(3x,
y)的方式变换,
求变换后所得图形中对应点的坐标.画出变换后图形,
它与原图形有何关系?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
A′
B′
C′
在平面直角坐标系中,
在作(x,
y)→(ax,
by)变换时,
当
a
=
b
≠
0
时为相似变换.
随堂演练
△ABC
的顶点坐标为
A(0,
2),
B(-3,
5),
C(-6,
3).
按如下方式对△ABC
进行变换:
(x,
y)→(2x,
2y);
(x,
y)→(-2x,
-2y).
画出变换后的图形,
它与原图形相似吗?为什么?
(x,
y)→(2x,
2y);
O
x
y
-12
-11
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
A
B
C
A′
B′
C′
A(0,
2),
B(-3,
5),
C(-6,
3).
(2)
(x,
y)→(-2x,
-2y).
O
-2
-4
-6
2
4
6
8
10
12
2
4
6
-2
-4
-6
-8
-10
x
y
A
B
C
A′
B′
C′
A(0,
2),
B(-3,
5),
C(-6,
3).
课堂小结
一般地,
在平面直角坐标系中,
如果以原点为位似中心,
新图形与原图形的相似比为
k,
那么与原图形上的点(x,y)对应的位似图形上的点的坐标为__________________.
(kx,
ky)或(-kx,
-ky)
在平面直角坐标系中在作
(x,
y)?
(x,
ay)或(ax,
y)变换时,
叫伸缩变换.
课后作业
1.从教材习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
第2课时
平面直角坐标系中图形的位似变换
22.4
图形的位似变换
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
1.了解图形的位似概念,会判断简单的位似图形和位似中心.
2.理解位似图形的性质,能利用位似将一个图形放大或缩小,解决一些简单的实际问题.
【过程与方法】
采用引导、启发、合作、探究等方法,经历观察、发现、动手操作、归纳、交流等数学活动,获得知识,形成技能,发展思维,学会学习.
【情感态度】
使学生亲身经历位似图形概念形成的过程和位似图形性质的探索过程,感受数学学习内容的现实性、应用性.
【教学重点】
图形的位似概念、位似图形的性质及利用位似把一个图形放大或缩小.
【教学难点】
探索位似概念、位似图形的性质的过程及利用位似准确地把一个图形通过不同的方法放大或缩小.
新课导入
位似图形的定义:
如果两个图形不仅是相似图形,
而且每组对应点所在的直线都经过同一个点,
那么这样的两个图形叫做位似图形,
这个点叫做位似中心,这时的相似比又称为位似比.
画位似图形的步骤:
(1)确定位似中心点;
(2)将图形各顶点与位似中心连接(或延长);
(3)按位似比进行取点;
(4)顺次连接各点,所得的图形就是所求的图形.
如何把三角形ABC
放大为原来的
2
倍?
A
B
C
O
B1
A1
C1
OA1
=
2OA
OB1
=
2OB
OC1
=
2OC
新课探究
交流
如果把位似图形放到直角坐标系中,又如何去探究位似变换与坐标之间的关系呢?
如图,
在平面直角坐标系中,
△ABC
的顶点坐标分别为
A(1,1),
B(3,2),
C(4,1).以原点
O
为位似中心,
相似比为3,
作△ABC
的位似图形.
观察对应顶点坐标的变化,
你有什么发现?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
连接OA,
OB,
OC,
分别延长
OA,
OB,
OC
至点
A′,
B′,
C′,
使
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
连接
AB,
BC,
CA,
那么△A′B′C′
就是所求的△ABC
的位似图形.
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
可以看到,
位似变换后点
A,
B,
C
的对应点分别为点A′(3,3)
,B′(9,6)
,C′(12,3).
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
对比下图中变换前后各对应点的坐标,你可以发现什么?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
5
6
7
A′
B′
C′
在平面直角坐标系中,
如果位似变换是以原点
O
为位似中心,
相似比为
k(k>0),
原图形上点的坐标为(x,y),
那么同向位似图形对应点的坐标为(kx,
ky)(k>0).
利用这个性质作同向位似图形就相当简单,
只要把图形上各点的坐标都乘以一个固定的数
k(k>0),
就可以得到相似比为k(k>0)的同向位似图形.
O
x
y
A
B
C
B′
A′
C′
取
k
=3,
对图中的△ABC
进行变换,
看看结果如何?
这样得到的图形叫做反向位似图形.
O
x
y
A
B
C
B′
A′
C′
想一想:它与
k
=
3
时的变换结果有什么不同?
思考1:
将图中的△ABC,
按(x,
y)→
的方式变换,
求变换后所得图形中对应点的坐标.画出变换后图形,
它与原图形有何关系?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
A′
B′
C′
思考2:
将图中的△ABC,
按(x,
y)→(3x,
y)的方式变换,
求变换后所得图形中对应点的坐标.画出变换后图形,
它与原图形有何关系?
O
x
y
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
1
2
3
4
A′
B′
C′
在平面直角坐标系中,
在作(x,
y)→(ax,
by)变换时,
当
a
=
b
≠
0
时为相似变换.
随堂演练
△ABC
的顶点坐标为
A(0,
2),
B(-3,
5),
C(-6,
3).
按如下方式对△ABC
进行变换:
(x,
y)→(2x,
2y);
(x,
y)→(-2x,
-2y).
画出变换后的图形,
它与原图形相似吗?为什么?
(x,
y)→(2x,
2y);
O
x
y
-12
-11
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
A
B
C
A′
B′
C′
A(0,
2),
B(-3,
5),
C(-6,
3).
(2)
(x,
y)→(-2x,
-2y).
O
-2
-4
-6
2
4
6
8
10
12
2
4
6
-2
-4
-6
-8
-10
x
y
A
B
C
A′
B′
C′
A(0,
2),
B(-3,
5),
C(-6,
3).
课堂小结
一般地,
在平面直角坐标系中,
如果以原点为位似中心,
新图形与原图形的相似比为
k,
那么与原图形上的点(x,y)对应的位似图形上的点的坐标为__________________.
(kx,
ky)或(-kx,
-ky)
在平面直角坐标系中在作
(x,
y)?
(x,
ay)或(ax,
y)变换时,
叫伸缩变换.
课后作业
1.从教材习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
