第22章 相似形 章末复习 课件(共26张PPT)
文档属性
| 名称 | 第22章 相似形 章末复习 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 20:04:08 | ||
图片预览








文档简介
(共26张PPT)
章末复习
第22章
相似形
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
掌握本章知识,能熟练运用有关性质和判定,解决具体问题.
【过程与方法】
通过回顾和梳理本章知识了解与图形的相似有关的知识.
【情感态度】
在应用本章知识解决具体问题过程中提高学生分析问题、解决问题的能力.
【教学重点】
相似图形的特征与识别,相似三角形的有关概念及相似的表示方法和相似比的概念.
【教学难点】
能熟练运用有关性质和判定解决实际问题.
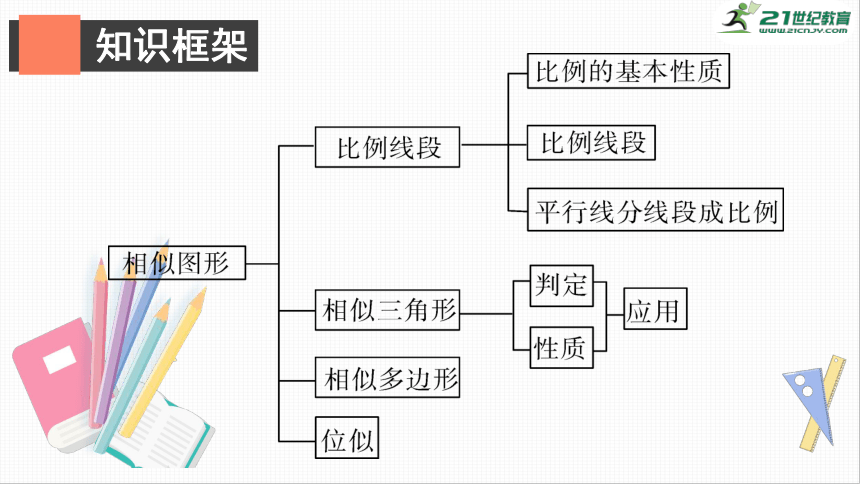
知识框架
主要知识回顾
1.两条线段的比
_______________去度量两条线段
a,
b,
得到的_________________叫做这两条线段的比.
用同一长度单位
两条线段长度的比
2.成比例线段
在四条线段
a
,b
,c
,d
中,
如果其中两条线段a
,b
的比,
等于另外两条线段
c
,d
的比,
即____________________,
那么这四条线段叫做成比例线段.
(或a∶b
=
c∶d)
下列各组线段的长度成比例的是(
)
练习
A.2,
3,
4,
1
B.1.5,
2.5,
6.5,
4.5
C.
1.1,
2.2,
3.3,
4.4
D.
1,
2,
2,
4
D
3.比例的性质
(1)基本性质:
如果
,
那么_______________.
ad
=
bc(b,
d≠0)
(2)合比性质:
如果
,那么_________________.
(3)等比性质:
如果
,且
那么_________________.
b1+b2+···+bn≠0,
填空:
练习
(1)已知
4a-3b=0,
则
_____.
(2)已知
,
则
___;
____.
4.相似三角形
(1)定义:
对应角相等、对应边成比例的三角形叫做相似三角形.
(2)相似比:
相似三角形的对应边的比,叫做相似三角形的相似比.
定理1:
(3)判定:
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
定理2:
如果一个三角形的两条边与另一个三角形的两条边对应成比例,
并且夹角相等,那么这两个三角形相似.
定理3:
如果一个三角形的三条边与另一个三角形的三条边对应成比例,
那么这两个三角形相似.
对于两个直角三角形,除上述判定定理外,还有:
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
(4)性质:
对应角_____,
对应边_______;
对应______、对应________、对应____________、和周长比都等于相似比.
相等
成比例
高的比
中线的比
角平分线的比
面积比等于_______________.
相似比的平方
5.位似图形
如果两个相似图形的每组对应点所在的直线都交于一点,
那么这样的两个图形叫做位似图形,
这个交点叫做位似中心,
这时两个相似图形的相似比又叫做它们的位似比.
随堂演练
1.
若
,
则
m
=_____.
2.
在△ABC中,
AB=AC=27,
D
在AC上,
且BD=BC=18,
DE//BC
交AB于E,
则
DE
=______.
A
B
C
E
D
10
3.
如图,
AB//CD,
AO=4,
BC=9,
OC=6,
求
OD
的长.
A
B
C
D
O
利用△AOB∽△DOC可求得OD=8.
4.已知:
如图,
在△ABC中,
D
为
AB
的中点,
E
为
AC
上的一点,
DE
延长线交
BC
延长线于点
F.
A
B
C
E
F
D
求证:
A
B
C
E
F
D
证明
过点
B
作
BH//AC,
交
FD
延长线于
H
点.
∵
BH//AC
,
∴
∠HBD=∠DAE,∠HDB=∠EDA
H
又∵BD
=
AD
∴△HDB≌△EDA
∴HB=EA
又∵∠H=∠CEF,∠F=∠F
A
B
C
E
F
D
H
∴△HBF∽△ECF
∴
2.7
E
C
8.7
A
B
1.8
(单位:
m)
D
5.
如图,
阳光通过窗口照到室内,
在地上留下
2.7m
宽的亮区.
已知亮区一边到窗下墙脚距离CE为
8.7m,
窗口高AB
为1.8m,
求窗口底边离地面的高度
BC
的值.
2.7
E
C
8.7
A
B
1.8
(单位:
m)
解
∵太阳光可以看成平行的光线.
∴△ACE∽△BCD,
D
∴
又∵AC
=
BC
+1.8,
EC=8.7,
DC=6.
∴BC
=4.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
章末复习
第22章
相似形
沪科版
九年级数学上册
上课课件
学习目标
【知识与技能】
掌握本章知识,能熟练运用有关性质和判定,解决具体问题.
【过程与方法】
通过回顾和梳理本章知识了解与图形的相似有关的知识.
【情感态度】
在应用本章知识解决具体问题过程中提高学生分析问题、解决问题的能力.
【教学重点】
相似图形的特征与识别,相似三角形的有关概念及相似的表示方法和相似比的概念.
【教学难点】
能熟练运用有关性质和判定解决实际问题.
知识框架
主要知识回顾
1.两条线段的比
_______________去度量两条线段
a,
b,
得到的_________________叫做这两条线段的比.
用同一长度单位
两条线段长度的比
2.成比例线段
在四条线段
a
,b
,c
,d
中,
如果其中两条线段a
,b
的比,
等于另外两条线段
c
,d
的比,
即____________________,
那么这四条线段叫做成比例线段.
(或a∶b
=
c∶d)
下列各组线段的长度成比例的是(
)
练习
A.2,
3,
4,
1
B.1.5,
2.5,
6.5,
4.5
C.
1.1,
2.2,
3.3,
4.4
D.
1,
2,
2,
4
D
3.比例的性质
(1)基本性质:
如果
,
那么_______________.
ad
=
bc(b,
d≠0)
(2)合比性质:
如果
,那么_________________.
(3)等比性质:
如果
,且
那么_________________.
b1+b2+···+bn≠0,
填空:
练习
(1)已知
4a-3b=0,
则
_____.
(2)已知
,
则
___;
____.
4.相似三角形
(1)定义:
对应角相等、对应边成比例的三角形叫做相似三角形.
(2)相似比:
相似三角形的对应边的比,叫做相似三角形的相似比.
定理1:
(3)判定:
如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.
定理2:
如果一个三角形的两条边与另一个三角形的两条边对应成比例,
并且夹角相等,那么这两个三角形相似.
定理3:
如果一个三角形的三条边与另一个三角形的三条边对应成比例,
那么这两个三角形相似.
对于两个直角三角形,除上述判定定理外,还有:
如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.
(4)性质:
对应角_____,
对应边_______;
对应______、对应________、对应____________、和周长比都等于相似比.
相等
成比例
高的比
中线的比
角平分线的比
面积比等于_______________.
相似比的平方
5.位似图形
如果两个相似图形的每组对应点所在的直线都交于一点,
那么这样的两个图形叫做位似图形,
这个交点叫做位似中心,
这时两个相似图形的相似比又叫做它们的位似比.
随堂演练
1.
若
,
则
m
=_____.
2.
在△ABC中,
AB=AC=27,
D
在AC上,
且BD=BC=18,
DE//BC
交AB于E,
则
DE
=______.
A
B
C
E
D
10
3.
如图,
AB//CD,
AO=4,
BC=9,
OC=6,
求
OD
的长.
A
B
C
D
O
利用△AOB∽△DOC可求得OD=8.
4.已知:
如图,
在△ABC中,
D
为
AB
的中点,
E
为
AC
上的一点,
DE
延长线交
BC
延长线于点
F.
A
B
C
E
F
D
求证:
A
B
C
E
F
D
证明
过点
B
作
BH//AC,
交
FD
延长线于
H
点.
∵
BH//AC
,
∴
∠HBD=∠DAE,∠HDB=∠EDA
H
又∵BD
=
AD
∴△HDB≌△EDA
∴HB=EA
又∵∠H=∠CEF,∠F=∠F
A
B
C
E
F
D
H
∴△HBF∽△ECF
∴
2.7
E
C
8.7
A
B
1.8
(单位:
m)
D
5.
如图,
阳光通过窗口照到室内,
在地上留下
2.7m
宽的亮区.
已知亮区一边到窗下墙脚距离CE为
8.7m,
窗口高AB
为1.8m,
求窗口底边离地面的高度
BC
的值.
2.7
E
C
8.7
A
B
1.8
(单位:
m)
解
∵太阳光可以看成平行的光线.
∴△ACE∽△BCD,
D
∴
又∵AC
=
BC
+1.8,
EC=8.7,
DC=6.
∴BC
=4.
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题.
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!
