陕西省黄陵中学2021届高三(高新部)上学期期中考试数学(理)试题 Word版含答案
文档属性
| 名称 | 陕西省黄陵中学2021届高三(高新部)上学期期中考试数学(理)试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 149.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-09 12:52:28 | ||
图片预览

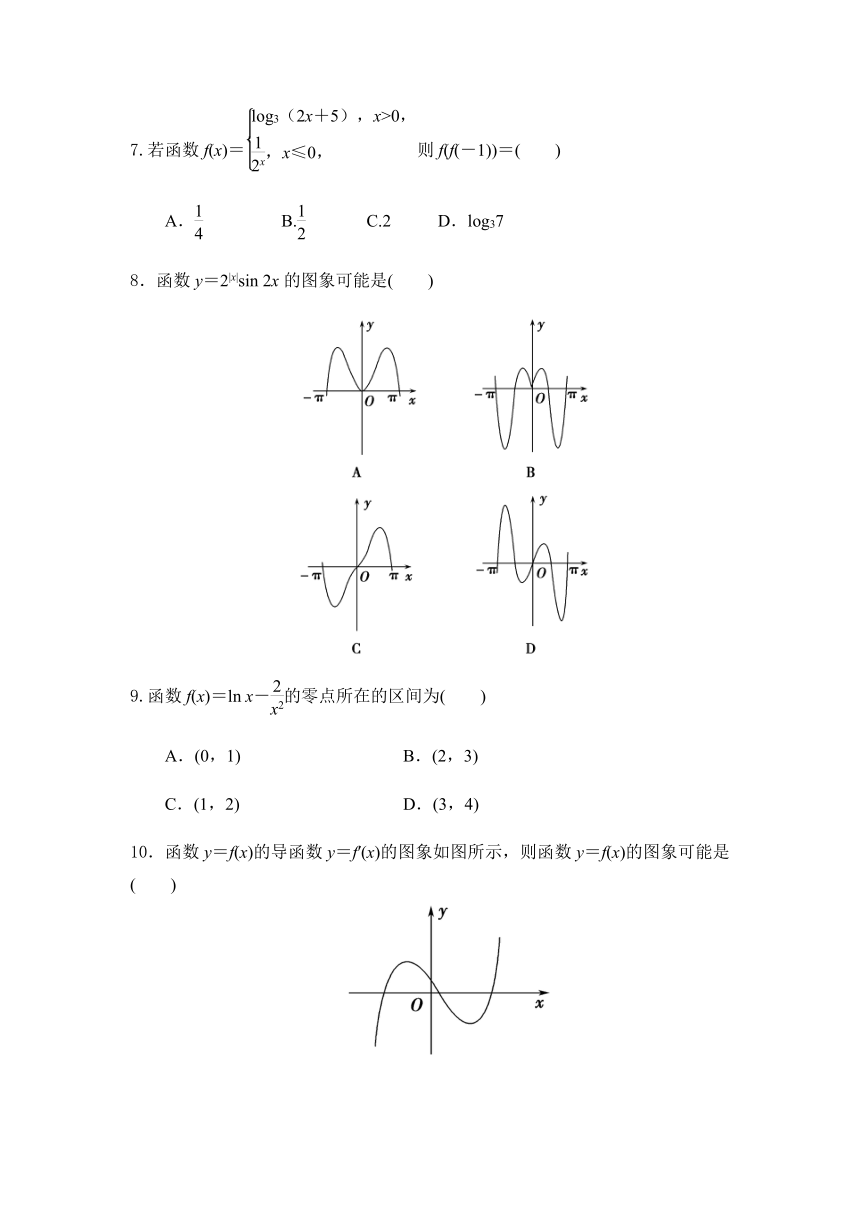


文档简介
黄陵中学2020-2021学年度第一学期
高新高三数学(理)期中考试试题
选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={0,2,3,5},B={2,3,4,5},则( )
A.{2,3,5}
B.{0,3,5}
C.{0,2,5}
D.{0,2,3}
设x∈R,则“3-x≥0”是“|x-1|≤1”的( )
A.必要不充分条件
B.
充分不必要条件
C.充要条件
D.既不充分也不必要条件
3.△ABC的内角A,B,C的对边分别为a,b,c,已知a=,c=2,cos
A=,则b=( )
A.
B.3
C.2
D.
4.“?x∈R,x2-πx≥0”的否定是( )
A.?x∈R,x2-πx<0
B.?x∈R,x2-πx≤0
C.?x0∈R,x-πx0<0
D.?x∈R,x-πx0≤0
5.下列函数中,其定义域和值域分别与函数y=10lg
x的定义域和值域相同的是( )
A.y=x
B.y=
C.y=2x
D.y=lg
x
6.已知函数f(x)在(-∞,+∞)单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是( )
A.[-2,2]
B.[-1,1]
C.
[1,3]
D.[0,4]
7.若函数f(x)=则f(f(-1))=( )
A.
B.
C.2
D.log37
8.函数y=2|x|sin
2x的图象可能是( )
9.函数f(x)=ln
x-的零点所在的区间为( )
A.(0,1)
B.(2,3)
C.(1,2)
D.(3,4)
10.函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)的图象可能是( )
11.已知sin=,则cos的值等于( )
A.-
B.
C.
D.-
12.已知函数f(x)=-2cos
ωx(ω>0)的图象向
左平移φ个单位,所得的部分函数
图象如图所示,则φ的值为( )
A.
B.
C.
D.
填空题(本大题共4小题,每题5分,共20分)
13.已知集合A={x|x2-5x-14≤0},集合B={x|m+114.已知f(x)是定义在R上的偶函数,且f(x+2)=-,当2≤x≤3时,f(x)=x,则f(105.5)=________.
15.在△ABC中,若b=a,B=2A,则△ABC为________三角形.
16.由抛物线y2=2x与直线y=x-4围成的平面图形的面积为________.
解答题(本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤.)
(本小题满分10分)
设p:实数x满足x2-4ax+3a2<0,q:实数x满足|x-3|<1.
若a=1,且p∧q为真,求实数x的取值范围;
18.(本小题满分12分)
已知函数f(x)=excos
x-x.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间上的最大值和最小值.
19.(本小题满分12分)
在△ABC中,角A,B,C的对边分别为a,b,c,已知A=,sin
B=3sin
C.
(1)求tan
C的值;
(2)若a=,求△ABC的面积.
20.(本小题12分)
设f(x)=loga(1+x)+loga(3-x)(a>0,a≠1),且f(1)=2.
(1)求a的值及f(x)的定义域;
(2)求f(x)在区间上的最大值
21.(本小题12分)
已知函数f(x)=4cos
ωx·sin(ω>0)的最小正周期是π.
(1)求函数f(x)在区间(0,π)上的单调递增区间;
(2)求f(x)在上的最大值.
22.(本小题满分12分)已知函数f(x)=ax+ln
x,x∈[1,e].
(1)若a=1,求f(x)的最大值;
(2)若f(x)≤0恒成立,求实数a的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
A
A
B
C
B
C
C
D
C
D
C
B
17.(本小题满分10分)解:(1)由x2-4ax+3a2<0得(x-3a)(x-a)<0,
当a=1时,1由|x-3|<1得-1即q为真时,实数x的取值范围是2若p∧q为真,则p真且q真,
所以实数x的取值范围是218.(本小题满分12分)解:(1)因为f(x)=excos
x-x,所以f(0)=1,
f′(x)=ex(cos
x-sin
x)-1,所以f′(0)=0,
所以y=f(x)在(0,f(0))处的切线方程为y=1.
(2)f′(x)=ex(cos
x-sin
x)-1,令g(x)=f′(x),
则g′(x)=-2sin
x·ex≤0在上恒成立,且仅在x=0处等号成立,
所以g(x)在上单调递减,
所以g(x)≤g(0)=0,所以f′(x)≤0且仅在x=0处等号成立,
所以f(x)在上单调递减,
所以f(x)max=f(0)=1,f(x)min=f=-.
19.(本小题满分12分)
解:(1)因为A=,所以B+C=,故sin=3sin
C,所以cos
C+sin
C=3sin
C,
即cos
C=sin
C,得tan
C=.
(2)由=,sin
B=3sin
C,得b=3c.
在△ABC中,由余弦定理,得
a2=b2+c2-2bccos
A=9c2+c2-2×(3c)×c×=7c2,又因为a=,所以c=1,b=3,
所以△ABC的面积为S=bcsin
A=.
20(本小题12分)
解:(1)因为f(1)=2,
所以loga4=2(a>0,a≠1),
所以a=2.
由得-1<x<3,
所以函数f(x)的定义域为(-1,3).
(2)f(x)=log2(1+x)+log2(3-x)
=log2[(1+x)(3-x)]
=log2[-(x-1)2+4],
所以当x∈(-1,1]时,f(x)是增函数;
当x∈(1,3)时,f(x)是减函数,
故函数f(x)在上的最大值是f(1)=log24=2.
21.(本小题12分)
解:(1)f(x)=4cos
ωx
=2sin
ωxcos
ωx-2cos2
ωx=sin
2ωx-cos
2ωx-1
=2sin-1,
因为f(x)的最小正周期为π,所以T==π.又ω>0,所以ω=1,
所以f(x)=2sin-1.
令-+2kπ≤2x-≤+2kπ(k∈Z),
得-+kπ≤x≤+kπ(k∈Z),
所以函数f(x)在(0,π)上的单调递增区间为和.
(2)当∈时,2x∈,≤2x-≤.
当2x-=,即x=时,f(x)取得最大值1.
22.(本小题满分12分)
解:(1)若a=1,则f(x)=x+ln
x,
f′(x)=1+=.
因为x∈[1,e],所以f′(x)>0,所以f(x)在[1,e]上为增函数,所以f(x)max=f(e)=e+1.
(2)依题意,不等式ax+ln
x≤0对x∈[1,e]恒成立,
等价于a≤-,x∈[1,e]恒成立.
令g(x)=-,x∈[1,e],
则g′(x)=,
因为x∈[1,e],所以g′(x)≤0,
所以g(x)在[1,e]上单调递减,
所以g(x)min=g(e)=-,所以a≤-.
所以实数a的取值范围是.
高新高三数学(理)期中考试试题
选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={0,2,3,5},B={2,3,4,5},则( )
A.{2,3,5}
B.{0,3,5}
C.{0,2,5}
D.{0,2,3}
设x∈R,则“3-x≥0”是“|x-1|≤1”的( )
A.必要不充分条件
B.
充分不必要条件
C.充要条件
D.既不充分也不必要条件
3.△ABC的内角A,B,C的对边分别为a,b,c,已知a=,c=2,cos
A=,则b=( )
A.
B.3
C.2
D.
4.“?x∈R,x2-πx≥0”的否定是( )
A.?x∈R,x2-πx<0
B.?x∈R,x2-πx≤0
C.?x0∈R,x-πx0<0
D.?x∈R,x-πx0≤0
5.下列函数中,其定义域和值域分别与函数y=10lg
x的定义域和值域相同的是( )
A.y=x
B.y=
C.y=2x
D.y=lg
x
6.已知函数f(x)在(-∞,+∞)单调递减,且为奇函数.若f(1)=-1,则满足-1≤f(x-2)≤1的x的取值范围是( )
A.[-2,2]
B.[-1,1]
C.
[1,3]
D.[0,4]
7.若函数f(x)=则f(f(-1))=( )
A.
B.
C.2
D.log37
8.函数y=2|x|sin
2x的图象可能是( )
9.函数f(x)=ln
x-的零点所在的区间为( )
A.(0,1)
B.(2,3)
C.(1,2)
D.(3,4)
10.函数y=f(x)的导函数y=f′(x)的图象如图所示,则函数y=f(x)的图象可能是( )
11.已知sin=,则cos的值等于( )
A.-
B.
C.
D.-
12.已知函数f(x)=-2cos
ωx(ω>0)的图象向
左平移φ个单位,所得的部分函数
图象如图所示,则φ的值为( )
A.
B.
C.
D.
填空题(本大题共4小题,每题5分,共20分)
13.已知集合A={x|x2-5x-14≤0},集合B={x|m+1
15.在△ABC中,若b=a,B=2A,则△ABC为________三角形.
16.由抛物线y2=2x与直线y=x-4围成的平面图形的面积为________.
解答题(本大题共6小题,共70分解答应写出文字说明、证明过程或演算步骤.)
(本小题满分10分)
设p:实数x满足x2-4ax+3a2<0,q:实数x满足|x-3|<1.
若a=1,且p∧q为真,求实数x的取值范围;
18.(本小题满分12分)
已知函数f(x)=excos
x-x.
(1)求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)在区间上的最大值和最小值.
19.(本小题满分12分)
在△ABC中,角A,B,C的对边分别为a,b,c,已知A=,sin
B=3sin
C.
(1)求tan
C的值;
(2)若a=,求△ABC的面积.
20.(本小题12分)
设f(x)=loga(1+x)+loga(3-x)(a>0,a≠1),且f(1)=2.
(1)求a的值及f(x)的定义域;
(2)求f(x)在区间上的最大值
21.(本小题12分)
已知函数f(x)=4cos
ωx·sin(ω>0)的最小正周期是π.
(1)求函数f(x)在区间(0,π)上的单调递增区间;
(2)求f(x)在上的最大值.
22.(本小题满分12分)已知函数f(x)=ax+ln
x,x∈[1,e].
(1)若a=1,求f(x)的最大值;
(2)若f(x)≤0恒成立,求实数a的取值范围.
1
2
3
4
5
6
7
8
9
10
11
12
A
A
B
C
B
C
C
D
C
D
C
B
17.(本小题满分10分)解:(1)由x2-4ax+3a2<0得(x-3a)(x-a)<0,
当a=1时,1
所以实数x的取值范围是2
x-x,所以f(0)=1,
f′(x)=ex(cos
x-sin
x)-1,所以f′(0)=0,
所以y=f(x)在(0,f(0))处的切线方程为y=1.
(2)f′(x)=ex(cos
x-sin
x)-1,令g(x)=f′(x),
则g′(x)=-2sin
x·ex≤0在上恒成立,且仅在x=0处等号成立,
所以g(x)在上单调递减,
所以g(x)≤g(0)=0,所以f′(x)≤0且仅在x=0处等号成立,
所以f(x)在上单调递减,
所以f(x)max=f(0)=1,f(x)min=f=-.
19.(本小题满分12分)
解:(1)因为A=,所以B+C=,故sin=3sin
C,所以cos
C+sin
C=3sin
C,
即cos
C=sin
C,得tan
C=.
(2)由=,sin
B=3sin
C,得b=3c.
在△ABC中,由余弦定理,得
a2=b2+c2-2bccos
A=9c2+c2-2×(3c)×c×=7c2,又因为a=,所以c=1,b=3,
所以△ABC的面积为S=bcsin
A=.
20(本小题12分)
解:(1)因为f(1)=2,
所以loga4=2(a>0,a≠1),
所以a=2.
由得-1<x<3,
所以函数f(x)的定义域为(-1,3).
(2)f(x)=log2(1+x)+log2(3-x)
=log2[(1+x)(3-x)]
=log2[-(x-1)2+4],
所以当x∈(-1,1]时,f(x)是增函数;
当x∈(1,3)时,f(x)是减函数,
故函数f(x)在上的最大值是f(1)=log24=2.
21.(本小题12分)
解:(1)f(x)=4cos
ωx
=2sin
ωxcos
ωx-2cos2
ωx=sin
2ωx-cos
2ωx-1
=2sin-1,
因为f(x)的最小正周期为π,所以T==π.又ω>0,所以ω=1,
所以f(x)=2sin-1.
令-+2kπ≤2x-≤+2kπ(k∈Z),
得-+kπ≤x≤+kπ(k∈Z),
所以函数f(x)在(0,π)上的单调递增区间为和.
(2)当∈时,2x∈,≤2x-≤.
当2x-=,即x=时,f(x)取得最大值1.
22.(本小题满分12分)
解:(1)若a=1,则f(x)=x+ln
x,
f′(x)=1+=.
因为x∈[1,e],所以f′(x)>0,所以f(x)在[1,e]上为增函数,所以f(x)max=f(e)=e+1.
(2)依题意,不等式ax+ln
x≤0对x∈[1,e]恒成立,
等价于a≤-,x∈[1,e]恒成立.
令g(x)=-,x∈[1,e],
则g′(x)=,
因为x∈[1,e],所以g′(x)≤0,
所以g(x)在[1,e]上单调递减,
所以g(x)min=g(e)=-,所以a≤-.
所以实数a的取值范围是.
同课章节目录
