2020年秋人教版九年级上册24.1.2《垂径定理》同步练习(Word版 含答案)
文档属性
| 名称 | 2020年秋人教版九年级上册24.1.2《垂径定理》同步练习(Word版 含答案) | 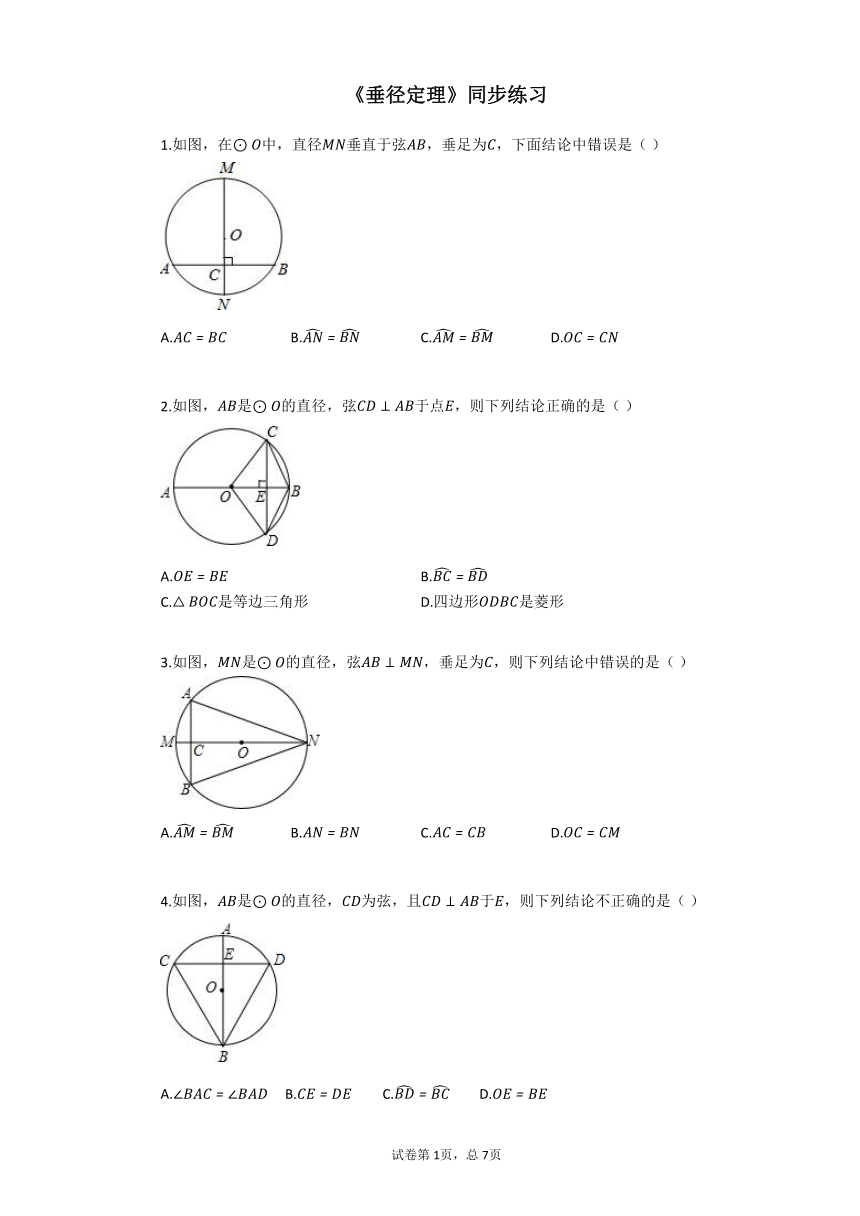 | |
| 格式 | docx | ||
| 文件大小 | 157.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-08 20:33:50 | ||
图片预览


文档简介
《垂径定理》同步练习
1.如图,在中,直径垂直于弦,垂足为,下面结论中错误是(
)
A.
B.
C.
D.
?
2.如图,是的直径,弦于点,则下列结论正确的是(
)
A.
B.
C.是等边三角形
D.四边形是菱形
3.如图,是的直径,弦,垂足为,则下列结论中错误的是(
)
A.
B.
C.
D.
?
4.如图,是的直径,为弦,且于,则下列结论不正确的是(
)
A.
B.
C.
D.
5.一条排水管的截面如图所示,已知排水管的截面圆半径,截面圆圆心到水面的距离是,则水面宽是(?
?
?
?
)
A.
B.
C.
D.
?
6.在圆柱形油槽内装有一些油.截面如图,圆柱形油槽直径为分米,油面宽为分米,如果再注入一些油?后,油面上升分米,油面宽变为(
)
A.分米
B.分米
C.分米
D.分米
?
7.如图,的弦垂直于,为垂足,,,且,则圆心到的距离是________.
?
8.如下图,在以为圆心的两个同心圆中,大圆的弦交小圆于和两点,,,则长为________.
9.半径是的圆中,垂直平分半径的弦长为________.
?
10.已知横断面直径为米的圆形下水管道的水面宽米,求下水管道中水的最大深度为________.
?
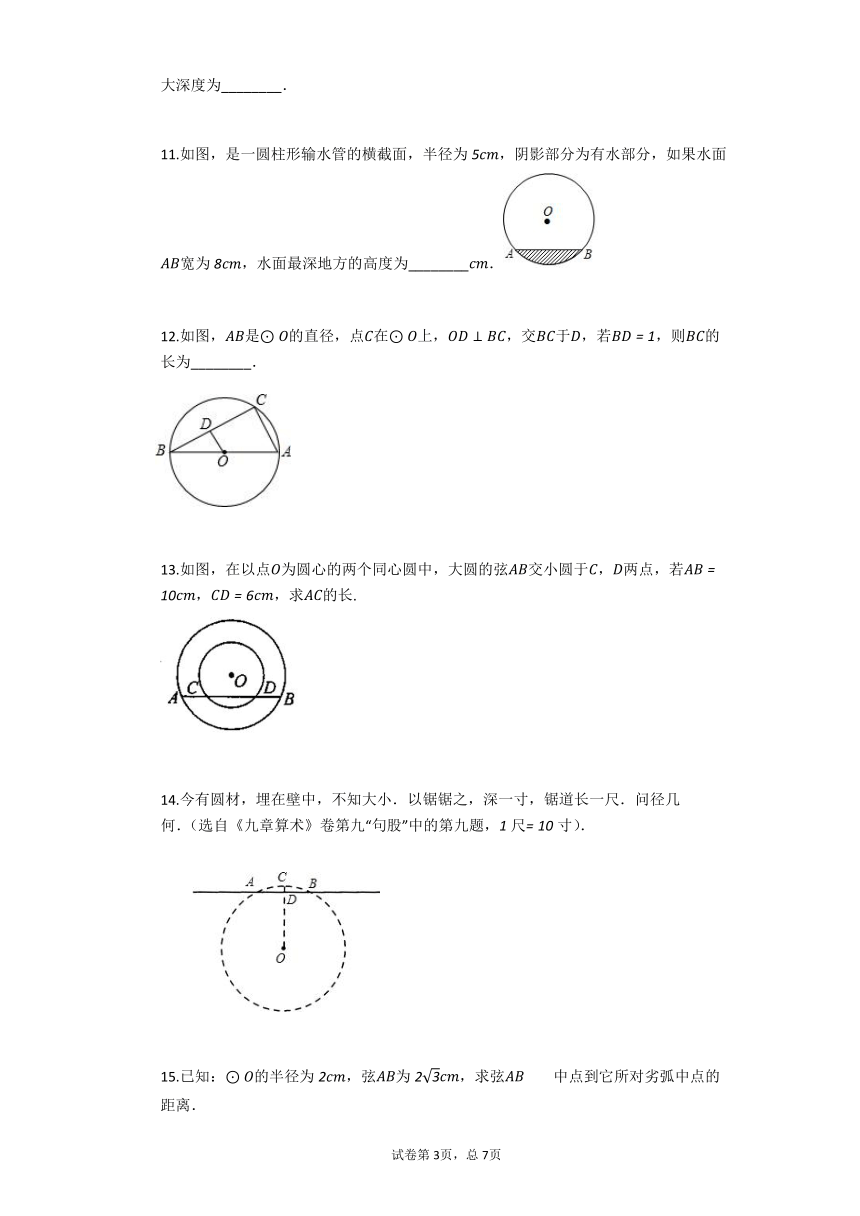
11.如图,是一圆柱形输水管的横截面,半径为,阴影部分为有水部分,如果水面宽为,水面最深地方的高度为________.
?
12.如图,是的直径,点在上,,交于,若,则的长为________.
?
13.如图,在以点为圆心的两个同心圆中,大圆的弦交小圆于,两点,若,,求的长.
?
14.今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.(选自《九章算术》卷第九“句股”中的第九题,尺寸).
?
15.已知:的半径为,弦为,求弦中点到它所对劣弧中点的距离.
?
16.用尺规作图(保留作图痕迹,不写作法)如图是一块破碎的圆形木盖,试确定它的圆心并作出它所在的圆.
?
17.如图,是一块残破的圆轮片,、、是圆弧上的三点.
作出弧所在的(不写作法,保留作图痕迹);
如果,,求该残破圆轮片的半径.
?
18.如图,水平放置的圈柱形水管道的截面半径是,其中水面高,求截面上有水部分的面积(结果保留)
参考答案
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】B
7.【答案】
8.【答案】
9.【答案】
10.【答案】米或米
11.【答案】
12.【答案】
13.【答案】
解:作,垂足为.
由垂径定理知,点是的中点,也是的中点,
∴
,,
∴
.
14.【答案】
解:本题用现在的数学语言表述是:“如图所示,为的直径,,垂足为,寸,尺,求直径长是多少寸?”
设直径的长为寸,则半径寸.
∵
为的直径,弦于,寸,
∴
寸,
连接,则寸,
根据勾股定理得,
解得,
(寸).
故所求直径为寸.
15.【答案】
如图.作半径于,连接,
∵
弦为,
∴
=,,
在中,,
∴
===,
即弦中点到它所对劣弧中点的距离为.
16.【答案】
解:
作圆的两条不平行的弦,然后作两条弦的中垂线,两中垂线的交点就是圆的圆心.
17.【答案】
解:①如图所示:
②如图,∵
,,
∴
,
又∵
,,
∴
,
∴
和是等边三角形,
∴
,
∵
,
∴
,
∴
是等边三角形,
∴
半径为.
18.【答案】
解:连接、,过作,交于点,
∵
,,
∴
,
∴
,
∴
∴
,
∴
,
∴
.
试卷第4页,总9页
试卷第5页,总9页
1.如图,在中,直径垂直于弦,垂足为,下面结论中错误是(
)
A.
B.
C.
D.
?
2.如图,是的直径,弦于点,则下列结论正确的是(
)
A.
B.
C.是等边三角形
D.四边形是菱形
3.如图,是的直径,弦,垂足为,则下列结论中错误的是(
)
A.
B.
C.
D.
?
4.如图,是的直径,为弦,且于,则下列结论不正确的是(
)
A.
B.
C.
D.
5.一条排水管的截面如图所示,已知排水管的截面圆半径,截面圆圆心到水面的距离是,则水面宽是(?
?
?
?
)
A.
B.
C.
D.
?
6.在圆柱形油槽内装有一些油.截面如图,圆柱形油槽直径为分米,油面宽为分米,如果再注入一些油?后,油面上升分米,油面宽变为(
)
A.分米
B.分米
C.分米
D.分米
?
7.如图,的弦垂直于,为垂足,,,且,则圆心到的距离是________.
?
8.如下图,在以为圆心的两个同心圆中,大圆的弦交小圆于和两点,,,则长为________.
9.半径是的圆中,垂直平分半径的弦长为________.
?
10.已知横断面直径为米的圆形下水管道的水面宽米,求下水管道中水的最大深度为________.
?
11.如图,是一圆柱形输水管的横截面,半径为,阴影部分为有水部分,如果水面宽为,水面最深地方的高度为________.
?
12.如图,是的直径,点在上,,交于,若,则的长为________.
?
13.如图,在以点为圆心的两个同心圆中,大圆的弦交小圆于,两点,若,,求的长.
?
14.今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何.(选自《九章算术》卷第九“句股”中的第九题,尺寸).
?
15.已知:的半径为,弦为,求弦中点到它所对劣弧中点的距离.
?
16.用尺规作图(保留作图痕迹,不写作法)如图是一块破碎的圆形木盖,试确定它的圆心并作出它所在的圆.
?
17.如图,是一块残破的圆轮片,、、是圆弧上的三点.
作出弧所在的(不写作法,保留作图痕迹);
如果,,求该残破圆轮片的半径.
?
18.如图,水平放置的圈柱形水管道的截面半径是,其中水面高,求截面上有水部分的面积(结果保留)
参考答案
1.【答案】D
2.【答案】B
3.【答案】D
4.【答案】D
5.【答案】D
6.【答案】B
7.【答案】
8.【答案】
9.【答案】
10.【答案】米或米
11.【答案】
12.【答案】
13.【答案】
解:作,垂足为.
由垂径定理知,点是的中点,也是的中点,
∴
,,
∴
.
14.【答案】
解:本题用现在的数学语言表述是:“如图所示,为的直径,,垂足为,寸,尺,求直径长是多少寸?”
设直径的长为寸,则半径寸.
∵
为的直径,弦于,寸,
∴
寸,
连接,则寸,
根据勾股定理得,
解得,
(寸).
故所求直径为寸.
15.【答案】
如图.作半径于,连接,
∵
弦为,
∴
=,,
在中,,
∴
===,
即弦中点到它所对劣弧中点的距离为.
16.【答案】
解:
作圆的两条不平行的弦,然后作两条弦的中垂线,两中垂线的交点就是圆的圆心.
17.【答案】
解:①如图所示:
②如图,∵
,,
∴
,
又∵
,,
∴
,
∴
和是等边三角形,
∴
,
∵
,
∴
,
∴
是等边三角形,
∴
半径为.
18.【答案】
解:连接、,过作,交于点,
∵
,,
∴
,
∴
,
∴
∴
,
∴
,
∴
.
试卷第4页,总9页
试卷第5页,总9页
同课章节目录
