高中数学人教A版必修2第二章2.1空间点、直线、平面的位置关系辅导讲义(Word版无答案)
文档属性
| 名称 | 高中数学人教A版必修2第二章2.1空间点、直线、平面的位置关系辅导讲义(Word版无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 477.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 08:11:50 | ||
图片预览




文档简介
1224280011341100
空间点、直线、平面的位置关系
学生姓名:
年级:
上课日期:
内容
摘要
1.
三个定理与三个推论;
2.
直线与直线的位置关系;
3.直线与面,面与面的位置关系.
教学过程
考点一:三个定理与三个推论
1.1
已知下列四个命题:
①
很平的桌面是一个平面;
②
一个平面的面积可以是m;
③
平面是矩形或平行四边形;
④
两个平面叠在一起比一个平面厚.
其中正确的命题有( )
A.个
B.个
C.个
D.个
1.2
下列命题正确的是( )
A.经过三点确定一个平面
B.经过一条直线和一个点确定一个平面
C.四边形确定一个平面
D.两两相交且不共点的三条直线确定一个平面
2.1
下面推理过程,错误的是(
)
A.
;
B.;
C.
;
D.
.
3.1
在正方体ABCD—A1B1C1D1中,对角线A1C与平面BDC1交于点O,AC,BD交于点M,
求证:点C1,O,M共线.
三个定理与三个推论
公理1:如果一条直线上有两点在一个平面内,那么直线在平面内。用途:常用于证明直线在平面内.
公理2:不共线的三点确定一个平面.
推论1:直线与直线外的一点确定一个平面.
推论2:两条相交直线确定一个平面.
推论3:两条平行直线确定一个平面.
用途:用于确定平面。
公理3:如果两个平面有一个公共点,那么它们还有公共点,这些公共点的集合是一条直线(两个平面的交线).用途:常用于证明线在面内,证明点在线上.
1.1正方体各面所在平面将空间分成________部分.
1.2
下列命题正确的是( )
A.经过三点确定一个平面
B.经过一条直线和一个点确定一个平面
C.四边形确定一个平面
D.两两相交且不共点的三条直线确定一个平面
1.3
下列命题中,不正确的是( )
①
一条直线和两条平行直线都相交,那么这三条直线共面;
②
每两条都相交但不共点的四条直线一定共面;
③
两条相交直线上的三个点确定一个平面;
④
两条互相垂直的直线共面.
A.①与②
B.③与④
C.①与③
D.②与④
1.4
一条直线和这条直线之外不共线的三点所能确定的平面的个数是(
)
A.
1个或3个
B.
1个或4个
C.
3个或4个
D.
1个、3个或4个
2.1
已知A、B表示不同的点,l表示直线,α、β表示不同的平面,则下列推理错误的是( )
A.A∈l,A∈α,B∈l,B∈α?l?α
B.A∈α,A∈β,B∈α,B∈β?α∩β=AB
C.l?α,A∈l?A?α
D.A∈α,A∈l,l?α?l∩α=A
3.1
空间四边形ABCD中,各边长均为1,若BD=1,则AC的取值范围是________.
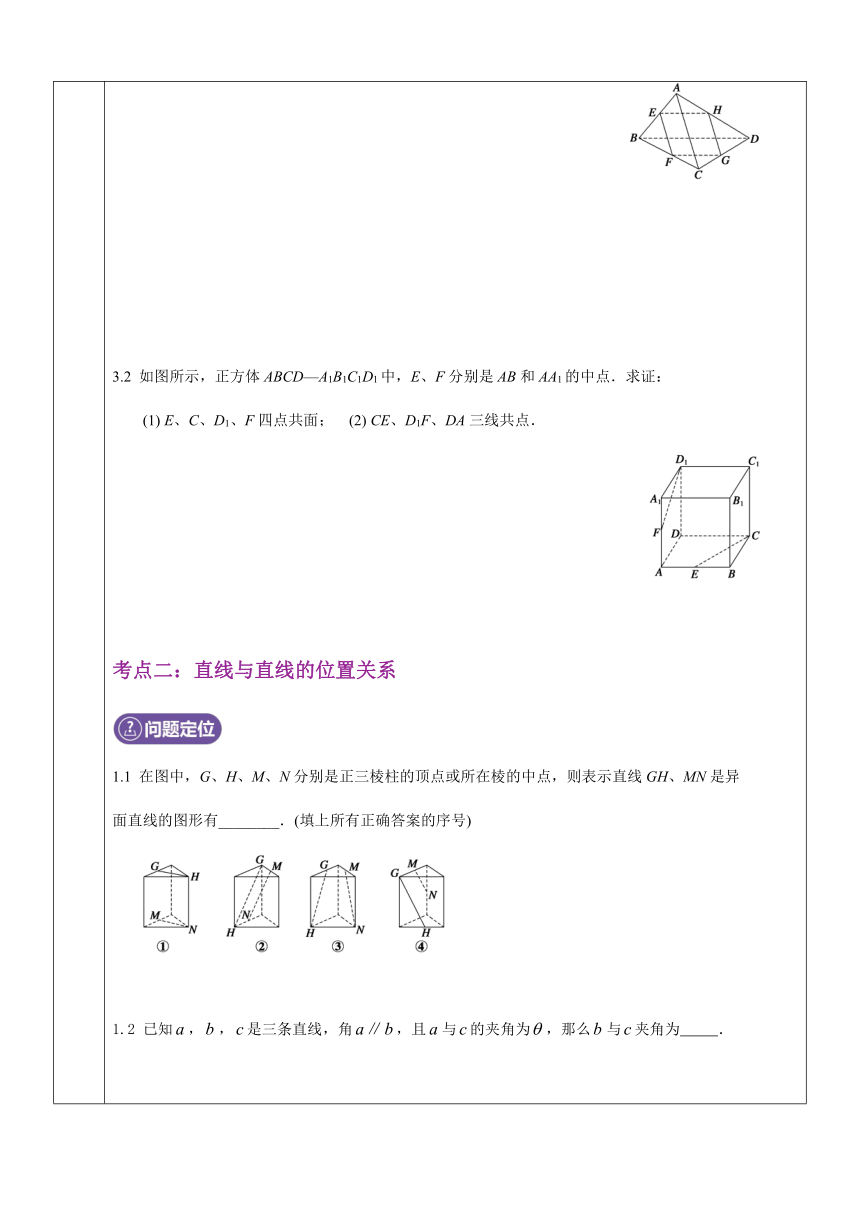
3.2
如图所示,正方体ABCD—A1B1C1D1中,E、F分别是AB和AA1的中点.求证:
(1)
E、C、D1、F四点共面;
(2)
CE、D1F、DA三线共点.
考点二:直线与直线的位置关系
1.1
在图中,G、H、M、N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH、MN是异
面直线的图形有________.(填上所有正确答案的序号)
1.2
已知,,是三条直线,角,且与的夹角为,那么与夹角为
.
2.1已知正方体ABCD-A1
B1
C1
D1中,E为C1D1的中点,则异面直线AE与BC所成角的余弦值______.
3.1
已知空间四边形ABCD中,E、H分别是边AB、AD的中点,F、G分别是边BC、CD的中点.
求证:(1)BC与AD是异面直线;(2)EG与FH相交.
1.
空间直线的位置关系:
2.
平行线的传递公理:平行于同一条直线的两条直线互相平行。符号表述:
3.
异面直线:
(1)定义:不同在任何一个平面内的两条直线——异面直线;
(2)判定定理:连平面内的一点与平面外一点的直线与这个平面内不过此点的直线是异面直线。
①
图形语言:
②
符号语言:
(3)
异面直线所成的角:
(1)范围:;(2)作异面直线所成的角:平移法.
(3)
如图,在空间任取一点O,过O作,则
所成的角为异面直线所成的角。
特别地,找异面直线所成的角时,经常把一条异面直线平移到另一条异面直线的特殊点(如线段中点,端点等)上,形成异面直线所成的角.
1.1
正方体的一条体对角线与正方体的棱可以组成异面直线的对数是(
)
A.
2
B.
3
C.
6
D.
12
1.2
已知a,b是异面直线,直线c平行于直线a,那么c与b( )
A.一定是异面直线
B.一定是相交直线
C.不可能是平行直线
D.不可能是相交直线
1.3
如图,已知长方体中,,,.
(1)
和所成的角是多少度?
(2)
和所成的角是多少度?
1.4
直三棱柱ABC-A1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成的角等于
( )
A.30°
B.45°
C.60°
D.90°
2.1
如果,是异面直线,直线与,都相交,那么这三条直线中的两条所确定的平面共有 个.
3.1
如图所示,正方体ABCD—A1B1C1D1中,M、N分别是A1B1、B1C1的中点.问:
(1)
AM和CN是否是异面直线?说明理由;
(2)
D1B和CC1是否是异面直线?说明理由.
3.2
正方体ABCD—A1B1C1D1中,
(1)
求AC与A1D所成角的大小;
(2)
若E、F分别为AB、AD的中点,求A1C1与EF所成角的大小.
考点三:直线与面,面与面的位置关系
1.1
已知两条相交直线,,,则与的位置关系是 .
1.2
如果三个平面两两相交,那么它们的交线有多少条?画出图形表示你的结论.
2.1若直线l上有两点P、Q到平面的距离相等,则直线l与平面的位置关系是( )
A、平行
B、相交
C、平行或相交
D、平行、相交或在平面内
2.2
若不共线的三点到平面的距离相等且不为0,则该三点确定的平面与平面的关系为(
)
A.平行
B.相交
C.平行或相交
D.重合[来源:学
1.
直线与平面的位置关系:
(1)
图形语言:
(2)
平面与平面的位置关系:
1.1
若直线不平行于平面,且,则下列结论成立的是(
)
A.内的所有直线与异面
B.内不存在与平行的直线
C.内存在唯一的直线与平行
D.内的直线与都相交
1.2
直线在平面外,则下列结论正确的是(
)
A.直线一定与平面平行
B.直线与至少有一个交点[]
C.直线一定与平面相交
D.直线与至多有一个公共点
1.3
三棱台的一条侧棱所在直线与其对面所在的平面之间的关系是(
)
A.相交
B.平行
C.线在平面内
D.平行或线在平面内
1.4
平面平面,直线,下列四个命题中正确的有________(填序号)。
①
和内的所有直线平行;
②
和内的无数条直线平行;
③
和内的任何一条直线都不垂直
;④
和无公共点。
1.5
平行于同一平面的两条直线的位置关系(
)
A.平行
B.相交
C.异面
D.平行、相交或异面
闯关进阶
第一关:基础达标
1.
已知点A,直线a,平面α.①A∈a,a?α?A?α;②A∈a,a∈α?A∈α;③A?a,a?α?A?α;
④A∈a,a?α?A∈α.以上表达中正确的个数是
( )
A.0个
B.1个
C.2个
D.3个
2.
给出下列命题:
①
和直线都相交的两条直线在同一个平面内;
②
三条两两相交的直线在同一平面内;
③
有三个不同公共点的两个平面重合;
④
两两平行的三条直线确定三个平面.
其中正确命题的个数是( )
A.0
B.1
C.2
D.3
3.
空间四个点A,B,C,D不共面,那么下列判断中正确的是
( )
A.A,B,C,D四点中必有三点共线
B.A,B,C,D四点中不存在三点共线
C.直线AB与CD相交
D.直线AB与CD平行
4.
三条直线相交于一点,可能确定的平面有( )
A.1个
B.2个
C.3个
D.1个或3个
5.
平面α、β相交,在α、β内各取两点,这四点都不在交线上,这四点能确定________个平面.
6.
如图,是长方体的一条棱,这个长方体中与垂直的棱共 条.
7.
若平面与平面相交,直线a在内,则直线a与的位置关系是(
)
A.a在内
B.a在外
C.a与平行或相交
D.a与平行或相交或a在内
8.
直线a∥平面α,直线b∥平面α,则a与b的位置关系为
(
)
A.相交
B.平行
C.异面
D.平行或异面或相交
9.
已知平面//平面,若两条直线m、n分别在平面、内,则m、n的位置关系不可能是(
)
A.平行
B.相交
C.异面
D.平行或异面
10.
在正方体ABCDA1B1C1D1中,E,F分别是AD,AA1的中点.
398018078740(1)求直线AB1和CC1所成的角的大小;
(2)求直线AB1和EF所成的角的大小.
11.
如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱CD、CC1的中点,则异面直线A1M与DN所成的角的大小是________.
第二关:举一反三
1.
如下图所示,用符号语言可表达为
( )
A.α∩β=m,n
?α,m∩n=A
B.α∩β=m,n∈α,m∩n=A
C.α∩β=m,n?α,A?m,A?n
D.α∩β=m,n∈α,A∈m,A∈n
2.
设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列四个命题,其中正确的命题是
( ).
①P∈a,P∈α?a?α ②a∩b=P,b?β?a?β ③a∥b,a?α,P∈b,P∈α?b?α
④α∩β=b,P∈α,P∈β?P∈b
A.①②
B.②③
C.①④
D.③④
3.
如图,三条直线两两平行且不共面,每两条确定一个平面,一共可以确定几个平面?如果三条直线相交于一点,它们最多可以确定几个平面?
4.
如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为________(注:把你认为正确的结论的序号都填上).
5.
分别和两条异面直线都相交的两条直线一定是( )
A.异面直线
B.相交直线
C.不相交直线
D.不平行直线
6.
若两条直线和一个平面相交成等角,则这两条直线的位置关系是( )
A.
平行
B.
异面
C.
相交
D.
平行、异面或相交
7.
在正方体ABCD—A1B1C1D1中,过顶点A1与正方体其他顶点的连线与直线BC1成60°角的条数为
(
)
A.1
B.2
C.3
D.4
8.
如图所示,正方体ABCD—A1B1C1D1中,M、N分别是A1B1、B1C1的中点.问:
(1)
AM和CN是否是异面直线?说明理由;
(2)
D1B和CC1是否是异面直线?说明理由.
9.
如图,在正方体ABCD-A1B1C1D1中,
(1)
求A1C1与B1C所成角的大小;
(2)
若E,F分别为AB,AD的中点,求A1C1与EF所成角的大小.
10.
正方体ABCD—A1B1C1D1中,
(1)
求AC与A1D所成角的大小;
(2)
若E、F分别为AB、AD的中点,求A1C1与EF所成角的大小.
第三关:融会贯通
1.
如图,ABCDA1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论错误的是________.
①
A,M,O三点共线
②
A,M,O,A1四点共面
③
A,O,C,M四点共面
④
B,B1,O,M四点共面
2.
若两个平面平行,则分别在这两个平行平面内的直线
( )
A.平行
B.异面
C.相交
D.平行或异面
3.
若不在同一直线上的三点A,B,C到平面α的距离相等,且A?α,则
( )
A.α∥平面ABC
B.△ABC中至少有一条边平行于α
C.△ABC中至少有两条边平行于α
D.△ABC中只可能有一条边与α相交
4.
已知直线a和平面α,β,α∩β=l,a?α,a?β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是
( )
A.相交或平行
B.相交或异面
C.平行或异面
D.相交、平行或异面
5.
如图,在正方体ABCD-A1B1C1D1中,过顶点A1与正方体其他顶点的连线与直线BC1成60°角的条数为
( )
A.1
B.2
C.3
D.4
6.
一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中
( ).
A.AB∥CD
B.AB与CD相交
C.AB⊥CD
D.AB与CD所成的角为60°
7.
已知正方体中,,分别为,的中点,,.
求证:
(1),,,四点共面;
(2)若交平面于点,则,,三点共线.
8.
如图是正方体的平面展开图,则在这个正方体中:
与平行.
与是异面直线.
与成角.
与垂直.
以上四个命题中,正确命题的序号是( )
A.,,
B.,
C.,
D.,,
9.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是________(写出所有正确命题的编号).
①当0<CQ<时,S为四边形;②当CQ=时,S为等腰梯形;③当CQ=时,S与C1D1的交点R满足C1R=;④当<CQ<1时,S为六边形;⑤当CQ=1时,S的面积为.
10.
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是________.
11.
如图1是一个正方体(如图2)的表面展开图的示意图,MN和PQ是两个面的对角线,请在正方体中将MN和PQ画出来,并就这个正方体解答下列问题:
(1)求MN和PQ所成角的大小;
(2)求四面体MNPQ的体积与正方体的体积之比.
320040043180
空间点、直线、平面的位置关系
学生姓名:
年级:
上课日期:
内容
摘要
1.
三个定理与三个推论;
2.
直线与直线的位置关系;
3.直线与面,面与面的位置关系.
教学过程
考点一:三个定理与三个推论
1.1
已知下列四个命题:
①
很平的桌面是一个平面;
②
一个平面的面积可以是m;
③
平面是矩形或平行四边形;
④
两个平面叠在一起比一个平面厚.
其中正确的命题有( )
A.个
B.个
C.个
D.个
1.2
下列命题正确的是( )
A.经过三点确定一个平面
B.经过一条直线和一个点确定一个平面
C.四边形确定一个平面
D.两两相交且不共点的三条直线确定一个平面
2.1
下面推理过程,错误的是(
)
A.
;
B.;
C.
;
D.
.
3.1
在正方体ABCD—A1B1C1D1中,对角线A1C与平面BDC1交于点O,AC,BD交于点M,
求证:点C1,O,M共线.
三个定理与三个推论
公理1:如果一条直线上有两点在一个平面内,那么直线在平面内。用途:常用于证明直线在平面内.
公理2:不共线的三点确定一个平面.
推论1:直线与直线外的一点确定一个平面.
推论2:两条相交直线确定一个平面.
推论3:两条平行直线确定一个平面.
用途:用于确定平面。
公理3:如果两个平面有一个公共点,那么它们还有公共点,这些公共点的集合是一条直线(两个平面的交线).用途:常用于证明线在面内,证明点在线上.
1.1正方体各面所在平面将空间分成________部分.
1.2
下列命题正确的是( )
A.经过三点确定一个平面
B.经过一条直线和一个点确定一个平面
C.四边形确定一个平面
D.两两相交且不共点的三条直线确定一个平面
1.3
下列命题中,不正确的是( )
①
一条直线和两条平行直线都相交,那么这三条直线共面;
②
每两条都相交但不共点的四条直线一定共面;
③
两条相交直线上的三个点确定一个平面;
④
两条互相垂直的直线共面.
A.①与②
B.③与④
C.①与③
D.②与④
1.4
一条直线和这条直线之外不共线的三点所能确定的平面的个数是(
)
A.
1个或3个
B.
1个或4个
C.
3个或4个
D.
1个、3个或4个
2.1
已知A、B表示不同的点,l表示直线,α、β表示不同的平面,则下列推理错误的是( )
A.A∈l,A∈α,B∈l,B∈α?l?α
B.A∈α,A∈β,B∈α,B∈β?α∩β=AB
C.l?α,A∈l?A?α
D.A∈α,A∈l,l?α?l∩α=A
3.1
空间四边形ABCD中,各边长均为1,若BD=1,则AC的取值范围是________.
3.2
如图所示,正方体ABCD—A1B1C1D1中,E、F分别是AB和AA1的中点.求证:
(1)
E、C、D1、F四点共面;
(2)
CE、D1F、DA三线共点.
考点二:直线与直线的位置关系
1.1
在图中,G、H、M、N分别是正三棱柱的顶点或所在棱的中点,则表示直线GH、MN是异
面直线的图形有________.(填上所有正确答案的序号)
1.2
已知,,是三条直线,角,且与的夹角为,那么与夹角为
.
2.1已知正方体ABCD-A1
B1
C1
D1中,E为C1D1的中点,则异面直线AE与BC所成角的余弦值______.
3.1
已知空间四边形ABCD中,E、H分别是边AB、AD的中点,F、G分别是边BC、CD的中点.
求证:(1)BC与AD是异面直线;(2)EG与FH相交.
1.
空间直线的位置关系:
2.
平行线的传递公理:平行于同一条直线的两条直线互相平行。符号表述:
3.
异面直线:
(1)定义:不同在任何一个平面内的两条直线——异面直线;
(2)判定定理:连平面内的一点与平面外一点的直线与这个平面内不过此点的直线是异面直线。
①
图形语言:
②
符号语言:
(3)
异面直线所成的角:
(1)范围:;(2)作异面直线所成的角:平移法.
(3)
如图,在空间任取一点O,过O作,则
所成的角为异面直线所成的角。
特别地,找异面直线所成的角时,经常把一条异面直线平移到另一条异面直线的特殊点(如线段中点,端点等)上,形成异面直线所成的角.
1.1
正方体的一条体对角线与正方体的棱可以组成异面直线的对数是(
)
A.
2
B.
3
C.
6
D.
12
1.2
已知a,b是异面直线,直线c平行于直线a,那么c与b( )
A.一定是异面直线
B.一定是相交直线
C.不可能是平行直线
D.不可能是相交直线
1.3
如图,已知长方体中,,,.
(1)
和所成的角是多少度?
(2)
和所成的角是多少度?
1.4
直三棱柱ABC-A1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成的角等于
( )
A.30°
B.45°
C.60°
D.90°
2.1
如果,是异面直线,直线与,都相交,那么这三条直线中的两条所确定的平面共有 个.
3.1
如图所示,正方体ABCD—A1B1C1D1中,M、N分别是A1B1、B1C1的中点.问:
(1)
AM和CN是否是异面直线?说明理由;
(2)
D1B和CC1是否是异面直线?说明理由.
3.2
正方体ABCD—A1B1C1D1中,
(1)
求AC与A1D所成角的大小;
(2)
若E、F分别为AB、AD的中点,求A1C1与EF所成角的大小.
考点三:直线与面,面与面的位置关系
1.1
已知两条相交直线,,,则与的位置关系是 .
1.2
如果三个平面两两相交,那么它们的交线有多少条?画出图形表示你的结论.
2.1若直线l上有两点P、Q到平面的距离相等,则直线l与平面的位置关系是( )
A、平行
B、相交
C、平行或相交
D、平行、相交或在平面内
2.2
若不共线的三点到平面的距离相等且不为0,则该三点确定的平面与平面的关系为(
)
A.平行
B.相交
C.平行或相交
D.重合[来源:学
1.
直线与平面的位置关系:
(1)
图形语言:
(2)
平面与平面的位置关系:
1.1
若直线不平行于平面,且,则下列结论成立的是(
)
A.内的所有直线与异面
B.内不存在与平行的直线
C.内存在唯一的直线与平行
D.内的直线与都相交
1.2
直线在平面外,则下列结论正确的是(
)
A.直线一定与平面平行
B.直线与至少有一个交点[]
C.直线一定与平面相交
D.直线与至多有一个公共点
1.3
三棱台的一条侧棱所在直线与其对面所在的平面之间的关系是(
)
A.相交
B.平行
C.线在平面内
D.平行或线在平面内
1.4
平面平面,直线,下列四个命题中正确的有________(填序号)。
①
和内的所有直线平行;
②
和内的无数条直线平行;
③
和内的任何一条直线都不垂直
;④
和无公共点。
1.5
平行于同一平面的两条直线的位置关系(
)
A.平行
B.相交
C.异面
D.平行、相交或异面
闯关进阶
第一关:基础达标
1.
已知点A,直线a,平面α.①A∈a,a?α?A?α;②A∈a,a∈α?A∈α;③A?a,a?α?A?α;
④A∈a,a?α?A∈α.以上表达中正确的个数是
( )
A.0个
B.1个
C.2个
D.3个
2.
给出下列命题:
①
和直线都相交的两条直线在同一个平面内;
②
三条两两相交的直线在同一平面内;
③
有三个不同公共点的两个平面重合;
④
两两平行的三条直线确定三个平面.
其中正确命题的个数是( )
A.0
B.1
C.2
D.3
3.
空间四个点A,B,C,D不共面,那么下列判断中正确的是
( )
A.A,B,C,D四点中必有三点共线
B.A,B,C,D四点中不存在三点共线
C.直线AB与CD相交
D.直线AB与CD平行
4.
三条直线相交于一点,可能确定的平面有( )
A.1个
B.2个
C.3个
D.1个或3个
5.
平面α、β相交,在α、β内各取两点,这四点都不在交线上,这四点能确定________个平面.
6.
如图,是长方体的一条棱,这个长方体中与垂直的棱共 条.
7.
若平面与平面相交,直线a在内,则直线a与的位置关系是(
)
A.a在内
B.a在外
C.a与平行或相交
D.a与平行或相交或a在内
8.
直线a∥平面α,直线b∥平面α,则a与b的位置关系为
(
)
A.相交
B.平行
C.异面
D.平行或异面或相交
9.
已知平面//平面,若两条直线m、n分别在平面、内,则m、n的位置关系不可能是(
)
A.平行
B.相交
C.异面
D.平行或异面
10.
在正方体ABCDA1B1C1D1中,E,F分别是AD,AA1的中点.
398018078740(1)求直线AB1和CC1所成的角的大小;
(2)求直线AB1和EF所成的角的大小.
11.
如图,在正方体ABCD-A1B1C1D1中,M、N分别是棱CD、CC1的中点,则异面直线A1M与DN所成的角的大小是________.
第二关:举一反三
1.
如下图所示,用符号语言可表达为
( )
A.α∩β=m,n
?α,m∩n=A
B.α∩β=m,n∈α,m∩n=A
C.α∩β=m,n?α,A?m,A?n
D.α∩β=m,n∈α,A∈m,A∈n
2.
设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列四个命题,其中正确的命题是
( ).
①P∈a,P∈α?a?α ②a∩b=P,b?β?a?β ③a∥b,a?α,P∈b,P∈α?b?α
④α∩β=b,P∈α,P∈β?P∈b
A.①②
B.②③
C.①④
D.③④
3.
如图,三条直线两两平行且不共面,每两条确定一个平面,一共可以确定几个平面?如果三条直线相交于一点,它们最多可以确定几个平面?
4.
如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为________(注:把你认为正确的结论的序号都填上).
5.
分别和两条异面直线都相交的两条直线一定是( )
A.异面直线
B.相交直线
C.不相交直线
D.不平行直线
6.
若两条直线和一个平面相交成等角,则这两条直线的位置关系是( )
A.
平行
B.
异面
C.
相交
D.
平行、异面或相交
7.
在正方体ABCD—A1B1C1D1中,过顶点A1与正方体其他顶点的连线与直线BC1成60°角的条数为
(
)
A.1
B.2
C.3
D.4
8.
如图所示,正方体ABCD—A1B1C1D1中,M、N分别是A1B1、B1C1的中点.问:
(1)
AM和CN是否是异面直线?说明理由;
(2)
D1B和CC1是否是异面直线?说明理由.
9.
如图,在正方体ABCD-A1B1C1D1中,
(1)
求A1C1与B1C所成角的大小;
(2)
若E,F分别为AB,AD的中点,求A1C1与EF所成角的大小.
10.
正方体ABCD—A1B1C1D1中,
(1)
求AC与A1D所成角的大小;
(2)
若E、F分别为AB、AD的中点,求A1C1与EF所成角的大小.
第三关:融会贯通
1.
如图,ABCDA1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,则下列结论错误的是________.
①
A,M,O三点共线
②
A,M,O,A1四点共面
③
A,O,C,M四点共面
④
B,B1,O,M四点共面
2.
若两个平面平行,则分别在这两个平行平面内的直线
( )
A.平行
B.异面
C.相交
D.平行或异面
3.
若不在同一直线上的三点A,B,C到平面α的距离相等,且A?α,则
( )
A.α∥平面ABC
B.△ABC中至少有一条边平行于α
C.△ABC中至少有两条边平行于α
D.△ABC中只可能有一条边与α相交
4.
已知直线a和平面α,β,α∩β=l,a?α,a?β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是
( )
A.相交或平行
B.相交或异面
C.平行或异面
D.相交、平行或异面
5.
如图,在正方体ABCD-A1B1C1D1中,过顶点A1与正方体其他顶点的连线与直线BC1成60°角的条数为
( )
A.1
B.2
C.3
D.4
6.
一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中
( ).
A.AB∥CD
B.AB与CD相交
C.AB⊥CD
D.AB与CD所成的角为60°
7.
已知正方体中,,分别为,的中点,,.
求证:
(1),,,四点共面;
(2)若交平面于点,则,,三点共线.
8.
如图是正方体的平面展开图,则在这个正方体中:
与平行.
与是异面直线.
与成角.
与垂直.
以上四个命题中,正确命题的序号是( )
A.,,
B.,
C.,
D.,,
9.
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是________(写出所有正确命题的编号).
①当0<CQ<时,S为四边形;②当CQ=时,S为等腰梯形;③当CQ=时,S与C1D1的交点R满足C1R=;④当<CQ<1时,S为六边形;⑤当CQ=1时,S的面积为.
10.
如图所示,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是________.
11.
如图1是一个正方体(如图2)的表面展开图的示意图,MN和PQ是两个面的对角线,请在正方体中将MN和PQ画出来,并就这个正方体解答下列问题:
(1)求MN和PQ所成角的大小;
(2)求四面体MNPQ的体积与正方体的体积之比.
320040043180
