高中数学人教A版必修2课件:2.1.2空间中直线与直线之间的位置关系2异面直线所成角(共20张PPT)
文档属性
| 名称 | 高中数学人教A版必修2课件:2.1.2空间中直线与直线之间的位置关系2异面直线所成角(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 149.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-09 20:08:24 | ||
图片预览






文档简介
2.1.2 空间中直线与直线之间的位置关系
(2)异面直线所成角
Yesterday?once?more
公理1:如果一条直线上的两点在一个平面内,那么_________。
公理2:过_______的三点,有且只有一个平面。
推论1:经过____________,有且只有一个平面。
推论2:经过____直线,有且只有一个平面。
推论3:经过____直线,有且只有一个平面。
这条直线在此平面内
不在一条直线上
一条直线和这条直线外一点
两条相交
两条平行
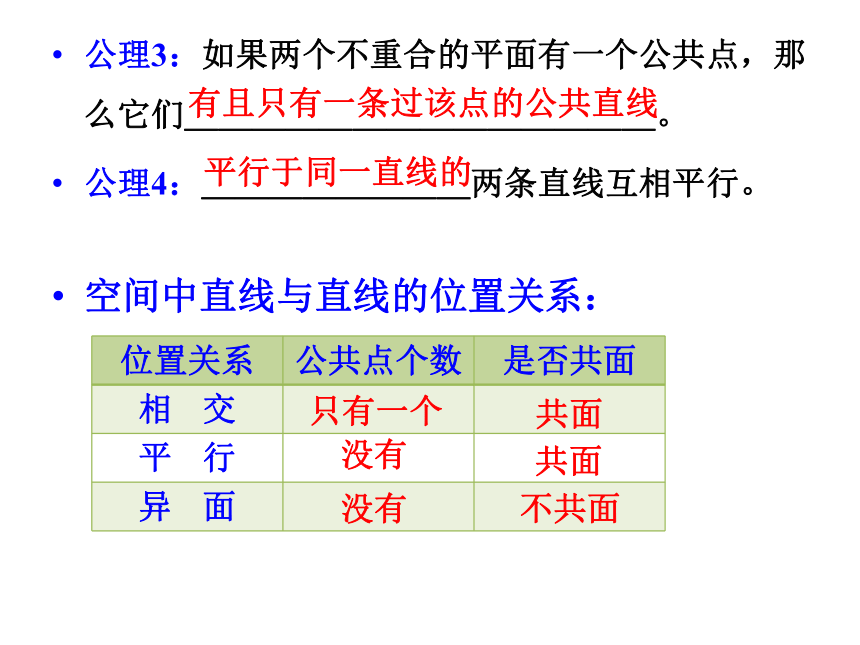
公理3:如果两个不重合的平面有一个公共点,那么它们______________。
公理4:________两条直线互相平行。
空间中直线与直线的位置关系:
有且只有一条过该点的公共直线
平行于同一直线的
{8799B23B-EC83-4686-B30A-512413B5E67A}位置关系
公共点个数
是否共面
相 交
平 行
异 面
没有
只有一个
没有
共面
不共面
共面
学习目标
1、熟练空间两条直线的位置关系;
2、掌握异面直线所成角的概念及异面直线垂直的概念,能求出一些较特殊的异面直线所成的角;
3、掌握等角定理及其应用。
重点:异面直线所成角的概念。
难点:异面直线所成角的定义的理解。
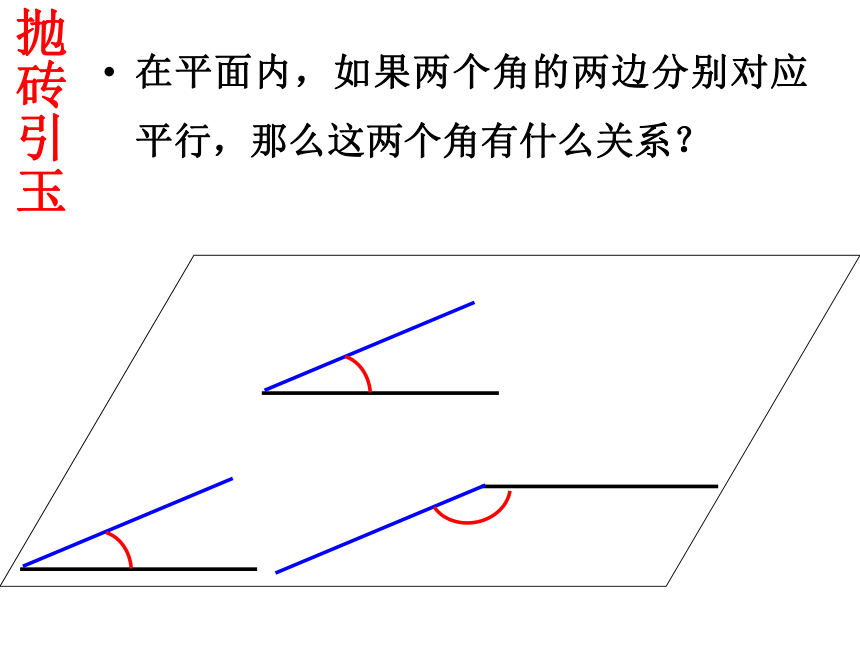
抛砖引玉
在平面内,如果两个角的两边分别对应平行,那么这两个角有什么关系?
抛砖引玉
在空间中,如果两个角的两边分别对应平行,结论是否仍然成立呢?
1、等角定理:
空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
【定理的推论】
如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等。
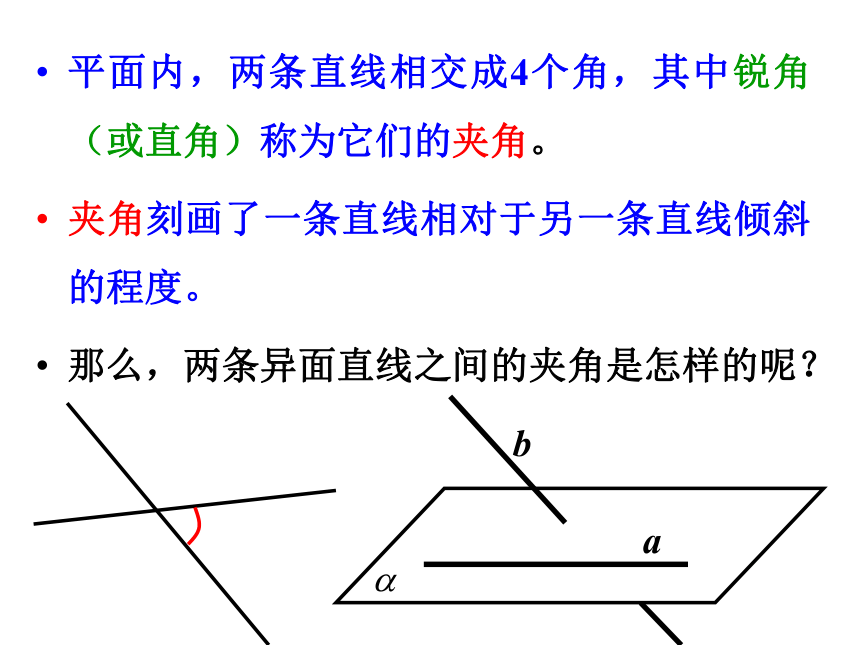
平面内,两条直线相交成4个角,其中锐角(或直角)称为它们的夹角。
夹角刻画了一条直线相对于另一条直线倾斜的程度。
那么,两条异面直线之间的夹角是怎样的呢?
a
b
自主学习(3min)
阅读教材P46—47,回答下列几个问题:
1、什么叫两条异面直线所成的角?
2、两条异面直线所成角的范围?
3、两条空间直线互相垂直的定义及表示方法?
2、异面直线所成角:
a
b
o
b'
a'
如图,已知两条异面直线a,b,经过空间任一点O作直线a'∥a,b'∥b,我们把a'与b'所成的锐角(或直角)叫做异面直线a,b所成的角(或夹角)。
平移
学生展示
举一反三
a'与b'所成角的大小与点O的位置有关吗?
为了简便,点O通常取在两条异面直线中的一条上。
异面直线所成角的实质:
异面直线经过平移到相交位置所成角。
空间图形
平面图形
O
3、异面直线所成角的范围:
如果两条异面直线所成的角是直角,
那么我们就说这两条直线互相垂直。
两条互相垂直的异面直线a、b,记作a⊥b。
我们规定:两条平行直线的夹角为_ 。
那么,两条异面直线所成的角的取值范围是:
0°
O
α
看图说话
1(1)长方体ABCD-A′B′C′D′中,有没有两条棱所在的直线是互相垂直的异面直线?
(2)如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直?
(3)垂直于同一条直线的两条直线是否平行?
B
A
D
C
A'
B'
D'
C'
精讲点拨
【例】如图,在正方体ABCD-A′B′C′D′中:
(1)哪些棱所在的直线与直线AA′垂直?
(2)哪些棱所在的直线与直线A′B垂直?
(3)直线A′B和CC′所成角是多少?
A′
B′
C′
D′
A
B
C
D
(3)∵BB′∥CC′,∴∠B′BA′就是异面直线A′B与CC′所成角,∴异面直线A′B与CC′所成角是450 。
解:(1) 直线AB,BC,CD,DA, A′B′ ,B′C′, C′D′, D′A′与直线AA′ 都垂直.
(2) 直线AD,BC, B′C′ ,A′D′与直线A′B都垂直.
求异面直线夹角的一般步骤是:“作—证—算—答”?
2、如图,已知正方体ABCD-A′B′C′D′?,求异面直线A′B和AC所成的角。
追踪训练
A′
B′
C′
D′
A
B
C
D
600
3、已知长方体ABCD-A1B1C1D1的底面是边长为4的正方形,高为2,点E、F分别是A1B1和BB1的中点,求异面直线EF与AD1所成角的余弦值。
B
A
C
D
E
F
A1
B1
C1
D1
提升训练
合作交流
A
F
E
D
C
B
M
4、在四面体ABCD中,E、F分别是棱AD、BC中点,已知AB=4,CD=2,EF= ,求异面直线AB和CD所成的角。
600
4、在四面体ABCD中,E、F分别是棱AD、BC上的点,且 ,已知AB=CD=3,EF= ,求异面直线AB和CD所成的角。
合作交流
A
F
E
D
C
B
M
600
知识盘点
1、等角定理;
2、异面直线夹角的概念;
3、求异面直线的夹角的一般步骤是:
“作—证—算—答”
课后作业
写本上:教材P48—练习2;
写书上:教材P48—练习1
教材P51—习题A组3 ,4
(2)异面直线所成角
Yesterday?once?more
公理1:如果一条直线上的两点在一个平面内,那么_________。
公理2:过_______的三点,有且只有一个平面。
推论1:经过____________,有且只有一个平面。
推论2:经过____直线,有且只有一个平面。
推论3:经过____直线,有且只有一个平面。
这条直线在此平面内
不在一条直线上
一条直线和这条直线外一点
两条相交
两条平行
公理3:如果两个不重合的平面有一个公共点,那么它们______________。
公理4:________两条直线互相平行。
空间中直线与直线的位置关系:
有且只有一条过该点的公共直线
平行于同一直线的
{8799B23B-EC83-4686-B30A-512413B5E67A}位置关系
公共点个数
是否共面
相 交
平 行
异 面
没有
只有一个
没有
共面
不共面
共面
学习目标
1、熟练空间两条直线的位置关系;
2、掌握异面直线所成角的概念及异面直线垂直的概念,能求出一些较特殊的异面直线所成的角;
3、掌握等角定理及其应用。
重点:异面直线所成角的概念。
难点:异面直线所成角的定义的理解。
抛砖引玉
在平面内,如果两个角的两边分别对应平行,那么这两个角有什么关系?
抛砖引玉
在空间中,如果两个角的两边分别对应平行,结论是否仍然成立呢?
1、等角定理:
空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。
【定理的推论】
如果两条相交直线和另两条相交直线分别平行,那么这两条直线所成的锐角(或直角)相等。
平面内,两条直线相交成4个角,其中锐角(或直角)称为它们的夹角。
夹角刻画了一条直线相对于另一条直线倾斜的程度。
那么,两条异面直线之间的夹角是怎样的呢?
a
b
自主学习(3min)
阅读教材P46—47,回答下列几个问题:
1、什么叫两条异面直线所成的角?
2、两条异面直线所成角的范围?
3、两条空间直线互相垂直的定义及表示方法?
2、异面直线所成角:
a
b
o
b'
a'
如图,已知两条异面直线a,b,经过空间任一点O作直线a'∥a,b'∥b,我们把a'与b'所成的锐角(或直角)叫做异面直线a,b所成的角(或夹角)。
平移
学生展示
举一反三
a'与b'所成角的大小与点O的位置有关吗?
为了简便,点O通常取在两条异面直线中的一条上。
异面直线所成角的实质:
异面直线经过平移到相交位置所成角。
空间图形
平面图形
O
3、异面直线所成角的范围:
如果两条异面直线所成的角是直角,
那么我们就说这两条直线互相垂直。
两条互相垂直的异面直线a、b,记作a⊥b。
我们规定:两条平行直线的夹角为_ 。
那么,两条异面直线所成的角的取值范围是:
0°
O
α
看图说话
1(1)长方体ABCD-A′B′C′D′中,有没有两条棱所在的直线是互相垂直的异面直线?
(2)如果两条平行直线中的一条与某一条直线垂直,那么,另一条直线是否也与这条直线垂直?
(3)垂直于同一条直线的两条直线是否平行?
B
A
D
C
A'
B'
D'
C'
精讲点拨
【例】如图,在正方体ABCD-A′B′C′D′中:
(1)哪些棱所在的直线与直线AA′垂直?
(2)哪些棱所在的直线与直线A′B垂直?
(3)直线A′B和CC′所成角是多少?
A′
B′
C′
D′
A
B
C
D
(3)∵BB′∥CC′,∴∠B′BA′就是异面直线A′B与CC′所成角,∴异面直线A′B与CC′所成角是450 。
解:(1) 直线AB,BC,CD,DA, A′B′ ,B′C′, C′D′, D′A′与直线AA′ 都垂直.
(2) 直线AD,BC, B′C′ ,A′D′与直线A′B都垂直.
求异面直线夹角的一般步骤是:“作—证—算—答”?
2、如图,已知正方体ABCD-A′B′C′D′?,求异面直线A′B和AC所成的角。
追踪训练
A′
B′
C′
D′
A
B
C
D
600
3、已知长方体ABCD-A1B1C1D1的底面是边长为4的正方形,高为2,点E、F分别是A1B1和BB1的中点,求异面直线EF与AD1所成角的余弦值。
B
A
C
D
E
F
A1
B1
C1
D1
提升训练
合作交流
A
F
E
D
C
B
M
4、在四面体ABCD中,E、F分别是棱AD、BC中点,已知AB=4,CD=2,EF= ,求异面直线AB和CD所成的角。
600
4、在四面体ABCD中,E、F分别是棱AD、BC上的点,且 ,已知AB=CD=3,EF= ,求异面直线AB和CD所成的角。
合作交流
A
F
E
D
C
B
M
600
知识盘点
1、等角定理;
2、异面直线夹角的概念;
3、求异面直线的夹角的一般步骤是:
“作—证—算—答”
课后作业
写本上:教材P48—练习2;
写书上:教材P48—练习1
教材P51—习题A组3 ,4
