人教A版高中数学必修二3.3.3 点到直线的距离(二)课件(共15张PPT)
文档属性
| 名称 | 人教A版高中数学必修二3.3.3 点到直线的距离(二)课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 667.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 08:58:00 | ||
图片预览




文档简介
*
点到直线的距离
*
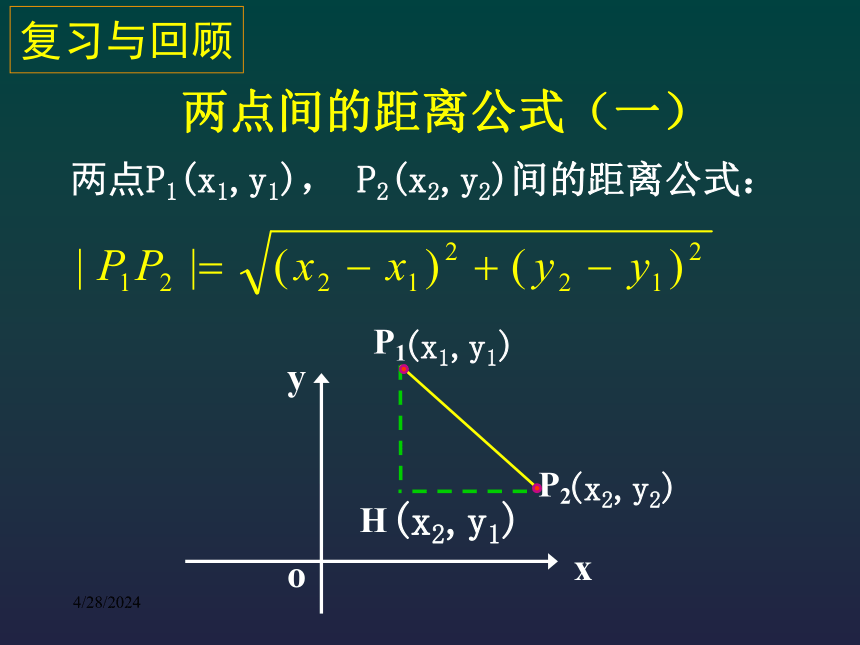
两点间的距离公式(一)
复习与回顾
H
(x2,y1)
y
x
o
P1
P2
(x1,y1)
(x2,y2)
两点P1(x1,y1), P2(x2,y2)间的距离公式:
*
两点间的距离(二)
(1)
若直线P1P2 与x轴平行或重合,即y1=y2 时 |P1P2|=|x2-x1|
若直线P1P2与y轴平行或重合,即x1=x2 时 | P1P2 |=|y2-y1|
(2)
复习与回顾
两点间的距离公式中特别的情况:
两点P1(x1,y1), P2(x2,y2)间的距离公式:
*
思考:
如图,已知点P和直线 l ,请你说出如何作出表示点P到直线 l 的距离的线段。
P
l
H
我们发现“点到直线的距离就是从直线外一点到这条直线的垂线段长度”。
点到直线的距离
*
点到直线的距离:从直线外一点到这条直线的垂线段长度。
练习1:求下列点到直线的距离
(1)P1(1,2), l1 :x=-3;
(2)O(0,0), l2 :2x+3y-6=0;
(3)P3(2,3), l3 :2x+3y-6=0;
试一试
点到直线的距离
*
点 的坐标
点 的坐标
两点间距离公式
点 之间的距离 ( 到 的距离)
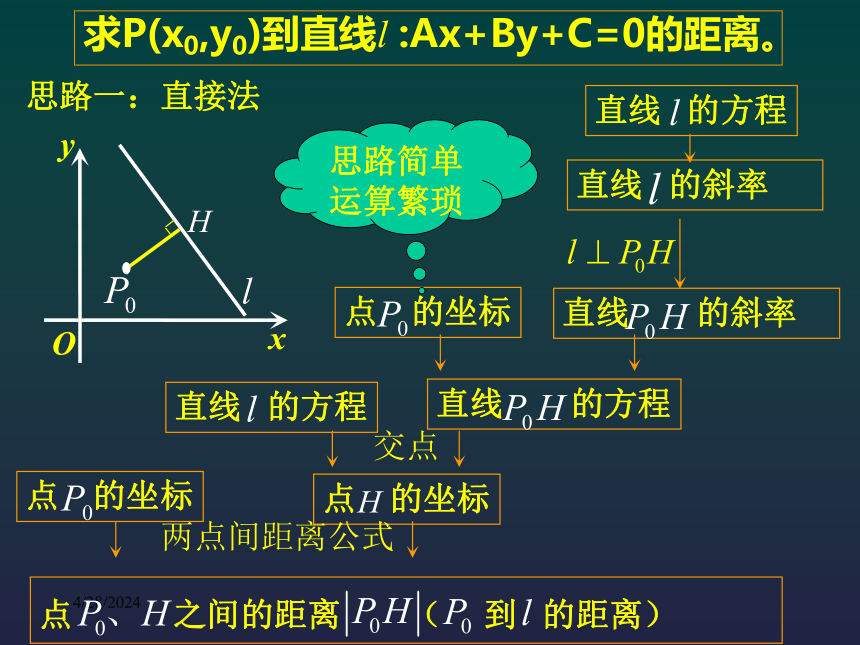
思路一:直接法
直线 的方程
直线 的斜率
直线 的方程
直线 的方程
交点
点 的坐标
直线 的斜率
x
y
O
思路简单运算繁琐
求P(x0,y0)到直线l :Ax+By+C=0的距离。
*
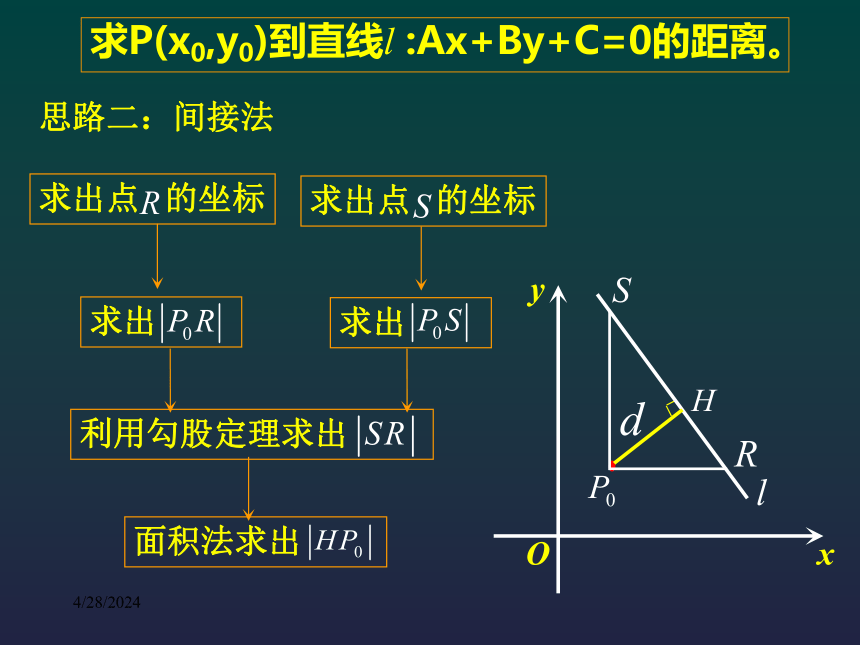
思路二:间接法
x
y
O
求出点 的坐标
面积法求出
利用勾股定理求出
求出
求出
求出点 的坐标
求P(x0,y0)到直线l :Ax+By+C=0的距离。
*
O
x
y
S
R
求P(x0,y0)到直线l :Ax+By+C=0的距离。
H
设S(n,y0),R(x0,m)
|PS|=|X0-n|,
|PR|=|y0-m|
因为,S,R均在l上
所以,An+By0+C=0,
Ax0+Bm+C=0
所以
所以
P(x0,y0)
(n,y0)
(x0,m)
*
点P(x0,y0)到直线l :Ax+By+C=0的距离公式
所以我们必须注意:利用点到直线的距离公式时,必须注意
先把直线方程化成一般式。
公式特点:(1)公式的分子部分绝对值里面的式子与直线的一般式方程等式左边部分形式相同;
(2)公式的分母部分根号里面是直线一般式形式中的x,y的系数的平方和;
*
例1 求点 到直线 的距离.
解:把直线 l 的方程化为一般式得 3x-2=0,所以,点P0到直线 l 的距离为:
思考:还有其他解法吗?
典型例题
O
y
x
l:3x=2
P(-1,2)
解法二:如图,直线3x=2平行于y
轴,直线l的方程可化为
所以,点P0到直线 l 的距离为:
*
例2 已知点 ,求 的面积.
解:如图,设 边上的高为 ,则
y
1
2
3
4
x
O
-1
1
2
3
边上的高 就是点 到 的距离.
典型例题
*
点 到 的距离
即:
因此,
典型例题
思考:还有其他解法吗?
边所在直线的方程为:
解:
例2 已知点 ,求 的面积.
y
1
2
3
4
x
O
-1
1
2
3
*
即:
因此,
典型例题
边所在直线的方程为:
例2 已知点 ,求 的面积.
y
1
2
3
4
x
O
-1
1
2
3
D
令y=0,解得D(4,0)
解法二:
延长AB与x轴相交于点D,
=5
*
练习
1.求坐标原点到下列直线的距离:
(1) 3x+2y-26=0; (2) x=y
2.求下列点到直线的距离:
(1) A(-2,3), 3x+4y+3=0
(2) B(1,0), x+y - =0
(3) C(1,-2), 4x+3y=0
*
平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式是
当A=0或B=0时,公式仍然成立.
小结
点到直线的距离
*
两点间的距离公式(一)
复习与回顾
H
(x2,y1)
y
x
o
P1
P2
(x1,y1)
(x2,y2)
两点P1(x1,y1), P2(x2,y2)间的距离公式:
*
两点间的距离(二)
(1)
若直线P1P2 与x轴平行或重合,即y1=y2 时 |P1P2|=|x2-x1|
若直线P1P2与y轴平行或重合,即x1=x2 时 | P1P2 |=|y2-y1|
(2)
复习与回顾
两点间的距离公式中特别的情况:
两点P1(x1,y1), P2(x2,y2)间的距离公式:
*
思考:
如图,已知点P和直线 l ,请你说出如何作出表示点P到直线 l 的距离的线段。
P
l
H
我们发现“点到直线的距离就是从直线外一点到这条直线的垂线段长度”。
点到直线的距离
*
点到直线的距离:从直线外一点到这条直线的垂线段长度。
练习1:求下列点到直线的距离
(1)P1(1,2), l1 :x=-3;
(2)O(0,0), l2 :2x+3y-6=0;
(3)P3(2,3), l3 :2x+3y-6=0;
试一试
点到直线的距离
*
点 的坐标
点 的坐标
两点间距离公式
点 之间的距离 ( 到 的距离)
思路一:直接法
直线 的方程
直线 的斜率
直线 的方程
直线 的方程
交点
点 的坐标
直线 的斜率
x
y
O
思路简单运算繁琐
求P(x0,y0)到直线l :Ax+By+C=0的距离。
*
思路二:间接法
x
y
O
求出点 的坐标
面积法求出
利用勾股定理求出
求出
求出
求出点 的坐标
求P(x0,y0)到直线l :Ax+By+C=0的距离。
*
O
x
y
S
R
求P(x0,y0)到直线l :Ax+By+C=0的距离。
H
设S(n,y0),R(x0,m)
|PS|=|X0-n|,
|PR|=|y0-m|
因为,S,R均在l上
所以,An+By0+C=0,
Ax0+Bm+C=0
所以
所以
P(x0,y0)
(n,y0)
(x0,m)
*
点P(x0,y0)到直线l :Ax+By+C=0的距离公式
所以我们必须注意:利用点到直线的距离公式时,必须注意
先把直线方程化成一般式。
公式特点:(1)公式的分子部分绝对值里面的式子与直线的一般式方程等式左边部分形式相同;
(2)公式的分母部分根号里面是直线一般式形式中的x,y的系数的平方和;
*
例1 求点 到直线 的距离.
解:把直线 l 的方程化为一般式得 3x-2=0,所以,点P0到直线 l 的距离为:
思考:还有其他解法吗?
典型例题
O
y
x
l:3x=2
P(-1,2)
解法二:如图,直线3x=2平行于y
轴,直线l的方程可化为
所以,点P0到直线 l 的距离为:
*
例2 已知点 ,求 的面积.
解:如图,设 边上的高为 ,则
y
1
2
3
4
x
O
-1
1
2
3
边上的高 就是点 到 的距离.
典型例题
*
点 到 的距离
即:
因此,
典型例题
思考:还有其他解法吗?
边所在直线的方程为:
解:
例2 已知点 ,求 的面积.
y
1
2
3
4
x
O
-1
1
2
3
*
即:
因此,
典型例题
边所在直线的方程为:
例2 已知点 ,求 的面积.
y
1
2
3
4
x
O
-1
1
2
3
D
令y=0,解得D(4,0)
解法二:
延长AB与x轴相交于点D,
=5
*
练习
1.求坐标原点到下列直线的距离:
(1) 3x+2y-26=0; (2) x=y
2.求下列点到直线的距离:
(1) A(-2,3), 3x+4y+3=0
(2) B(1,0), x+y - =0
(3) C(1,-2), 4x+3y=0
*
平面内一点P(x0,y0) 到直线Ax+By+C=0的距离公式是
当A=0或B=0时,公式仍然成立.
小结
