人教A版高中数学必修二3.3.3 点到直线的距离 应用课件(共17张PPT)
文档属性
| 名称 | 人教A版高中数学必修二3.3.3 点到直线的距离 应用课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-10 08:51:55 | ||
图片预览




文档简介
《点到直线的距离》
P
O
y
x
l
Q
P(x0,y0)
l:Ax+By+C=0
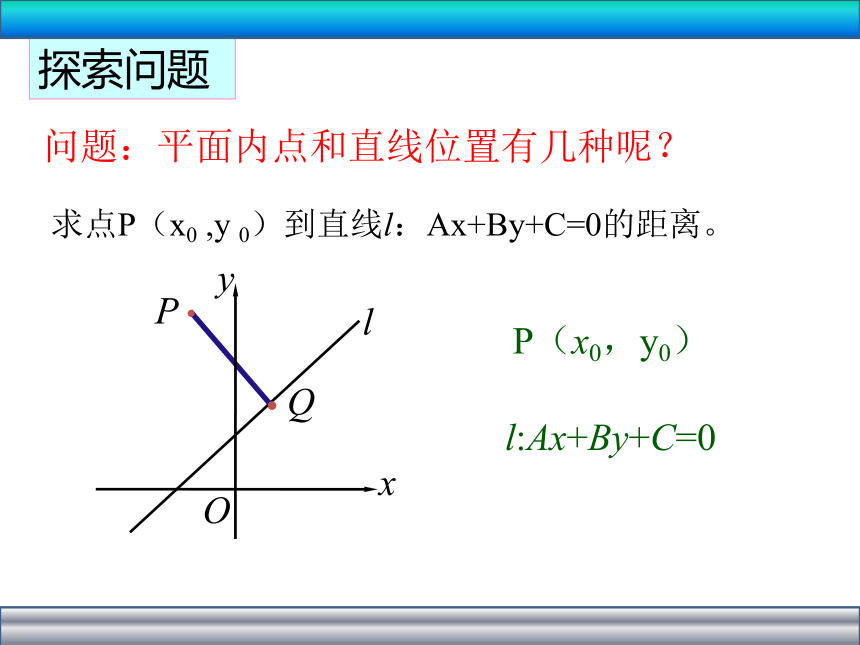
求点P(x0 ,y 0)到直线l:Ax+By+C=0的距离。
探索问题
问题:平面内点和直线位置有几种呢?
平面内两点间的距离公式是什么?
已知点 ,则
x
y
O
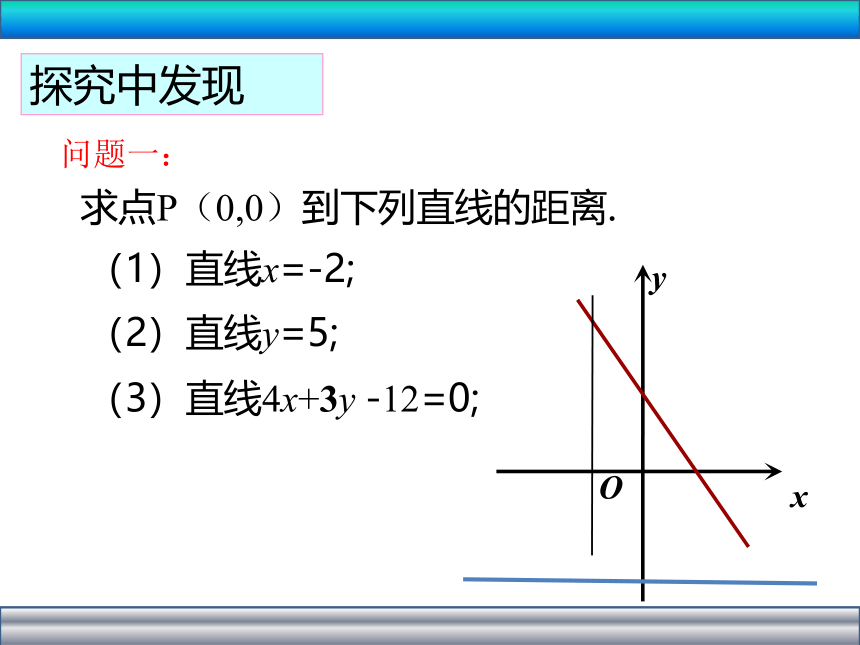
探究中发现
求点P(0,0)到下列直线的距离.
(1)直线x=-2;
(2)直线y=5;
(3)直线4x+3y -12=0;
问题一:
O
x
y
情境问题
求点P(-3,4)到下列直线的距离.
(1)直线x=-2;
(2)直线y=5;
(3)直线4x+3y -12=0;
问题二:
发现问题
O
x
y
P
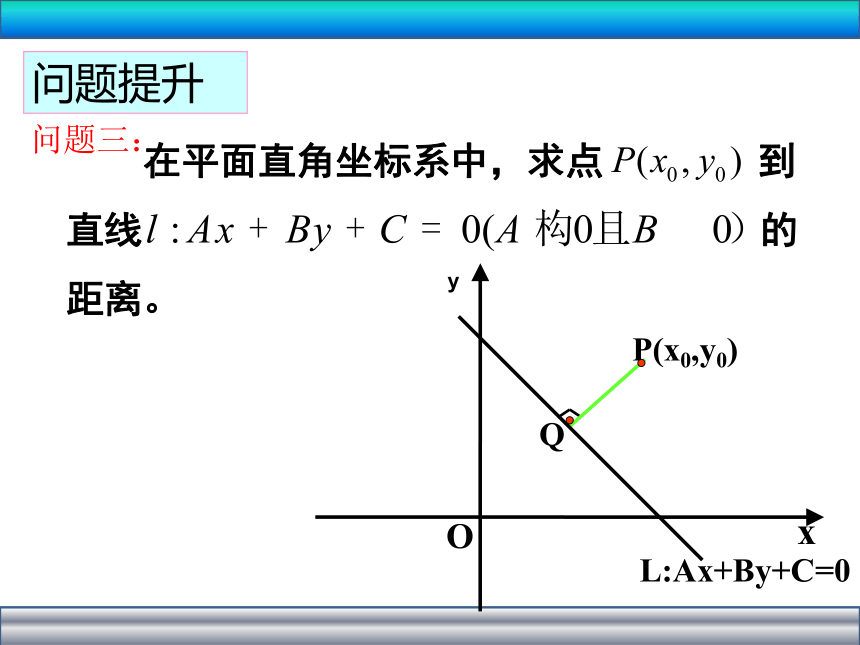
问题三:
在平面直角坐标系中,求点 到 直线 的距离。
问题提升
Q
x
P(x0,y0)
O
L:Ax+By+C=0
y
Q
x
y
P(x0,y0)
O
L:Ax+By+C=0
构造直角三角形求其高
(等面积法)
R
S
*
O
y
x
l
d
Q
P
R
S
由三角形面积公式可得:
P点坐标代入直线方程再取绝对值
x,y系数平方和的算术根,类似于用勾股定理求斜边
点到直线的距离公式
点 到直线 的距离公式为
求点P(0,0)到下列直线的距离.
(1)直线x=-2;
(2)直线y=5;
(3)直线4x+3y -12=0;
问题一:
O
x
y
提升后实践
例1:求点 到直线 的距离。
练习:求点 到下列直线的距离
(1)
3
0
x
y
例2:已知点A(1,3),B(3,1),C(-1,0),求:
的面积.
x
O
y
C
B
A
1.公式:平面内一点P(x0,y0) 到直线Ax+By+C=0
的距离公式是
课堂小结
3.公式的作用主要有:(1)求距离;(2)求参数;
(3)求点的坐标;(4)求直线方程.
2.数学思想:数形结合、转化与化归、分类讨论
思考:
(1)已知直线L过点A(2,1),并且点B(5,0)到直线L的距离为3,求直线L的方程
(2)能否利用点到直线的距离求两平行线之间的距离?
实践延伸
用勤奋书写有效的数学课堂,
用探究伴随每个同学的成长
1.公式:平面内一点P(x0,y0) 到直线Ax+By+C=0
的距离公式是
课堂小结
2.数学思想:数形结合、转化与化归、分类讨论
P
O
y
x
l
Q
P(x0,y0)
l:Ax+By+C=0
求点P(x0 ,y 0)到直线l:Ax+By+C=0的距离。
探索问题
问题:平面内点和直线位置有几种呢?
平面内两点间的距离公式是什么?
已知点 ,则
x
y
O
探究中发现
求点P(0,0)到下列直线的距离.
(1)直线x=-2;
(2)直线y=5;
(3)直线4x+3y -12=0;
问题一:
O
x
y
情境问题
求点P(-3,4)到下列直线的距离.
(1)直线x=-2;
(2)直线y=5;
(3)直线4x+3y -12=0;
问题二:
发现问题
O
x
y
P
问题三:
在平面直角坐标系中,求点 到 直线 的距离。
问题提升
Q
x
P(x0,y0)
O
L:Ax+By+C=0
y
Q
x
y
P(x0,y0)
O
L:Ax+By+C=0
构造直角三角形求其高
(等面积法)
R
S
*
O
y
x
l
d
Q
P
R
S
由三角形面积公式可得:
P点坐标代入直线方程再取绝对值
x,y系数平方和的算术根,类似于用勾股定理求斜边
点到直线的距离公式
点 到直线 的距离公式为
求点P(0,0)到下列直线的距离.
(1)直线x=-2;
(2)直线y=5;
(3)直线4x+3y -12=0;
问题一:
O
x
y
提升后实践
例1:求点 到直线 的距离。
练习:求点 到下列直线的距离
(1)
3
0
x
y
例2:已知点A(1,3),B(3,1),C(-1,0),求:
的面积.
x
O
y
C
B
A
1.公式:平面内一点P(x0,y0) 到直线Ax+By+C=0
的距离公式是
课堂小结
3.公式的作用主要有:(1)求距离;(2)求参数;
(3)求点的坐标;(4)求直线方程.
2.数学思想:数形结合、转化与化归、分类讨论
思考:
(1)已知直线L过点A(2,1),并且点B(5,0)到直线L的距离为3,求直线L的方程
(2)能否利用点到直线的距离求两平行线之间的距离?
实践延伸
用勤奋书写有效的数学课堂,
用探究伴随每个同学的成长
1.公式:平面内一点P(x0,y0) 到直线Ax+By+C=0
的距离公式是
课堂小结
2.数学思想:数形结合、转化与化归、分类讨论
